自適應神經模糊推理系統在信號去噪中的應用

李　娟

(運城學院　物理與電子工程系，山西　運城　044000)

?

自適應神經模糊推理系統在信號去噪中的應用

李娟

(運城學院物理與電子工程系，山西運城044000)

摘要：介紹了基于自適應神經模糊推理系統的語音去噪方法，這種算法把模糊系統理論和人工神經網絡相結合，繼承了二者的優點，通過神經網絡強大的自學能力，彌補了模糊推理系統非常依賴于操作人員的經驗的缺陷。有色噪聲是功率譜密度函數不為常數的噪聲，很難去除，仿真實驗證明：使用自適應神經模糊推理系統能較好的去除測量信號中的有色噪聲。

關鍵詞：自適應神經模糊推理系統；ANFIS；信號去噪

1965年美國加州大學的LA．Zadeh教授提出了模糊系統理論，由模糊集合理論、模糊邏輯、模糊控制和模糊推理等組成。其中模糊控制系統是處理模型未知的一種模型工具，廣泛應用于信號處理中，并十分具有應用前景，獲得了眾多學者專家的認同。但是也有缺點，設計模糊推理系統時雖然對于對象的模型沒有依賴，卻相當依賴于操作人員和專家的實際經驗和理論知識[1，2]。神經網絡(Neural Network，NN)是一種對信息進行分布式并行處理，可以模仿動物神經網絡行為特征的數學模型算法，這種算法具有非常強的自學習能力，但是也有缺點，在進行大量數據訓練后，才能處理結構化的知識。通過自學習，借助神經網絡的并行分布結構來估計從輸入到輸出的映射關系。

模糊控制系統與神經網絡在控制領域中是舉足輕重并且十分活躍的兩種算法，這兩種控制方法自身都有明顯的優點，但又存在一定的缺陷，把兩種方法相結合，吸取優點、摒棄缺點是控制系統理論推進的必然產物。把神經網絡的自學習訓練過程引入模糊控制系統，將構成一個帶有人類感覺和認知成分的自適應系統，是一種將人工神經網絡以及模糊邏輯相結合的新型推理系統結構，即自適應神經模糊推理系統[3～5](Adaptive Neural Fuzzy Inference System，ANFIS)。在信號處理領域，如果信號淹沒在噪聲中，而且噪聲影響較大，我們想得到純凈信號，如果噪聲是高斯白噪聲，可以使用線性濾波方法；如果噪聲是有色噪聲，那么使用非線性濾波就是一種更為有效的處理方式。而把人工神經網絡與模糊控制系統互相結合的自適應神經模糊推理系統(ANFIS)非常適合做為非線性濾波器[6，7]。

一、自適應神經模糊推理系統(ANFIS)

ANFIS也被稱之為Sugeno型模糊推理系統，它融合了模糊系統(Fuzzy Inference System，FIS)和神經網絡(NN)，在ANFIS的訓練過程中，通過神經網絡的自學習，模糊系統中輸入變量的隸屬度函數得到調整，與此同時系統根據輸入變量的數量自動生成響應的模糊規則，使得這個模糊系統模型的響應不斷逼近給定的訓練數據[8]。

具體實施步驟如下：

ANFIS由前件、后件組合而成，兩輸入對應單輸出系統的運算規則是:

IfX為G1，Y為H1，則Z1=p1X+q1Y+r1

If X為G2，Y為H2，則Z2=p2X+q2Y+r2

如果兩個輸入變量均采用高斯型隸屬度函數，用gxi(X,ai,bi)和gyi(Y,ci,di)來表示(其中i=1,2)，如圖1，一階Sugeno模糊系統表示一個兩輸入對應單輸出的演變過程，等效成ANFIS結構。

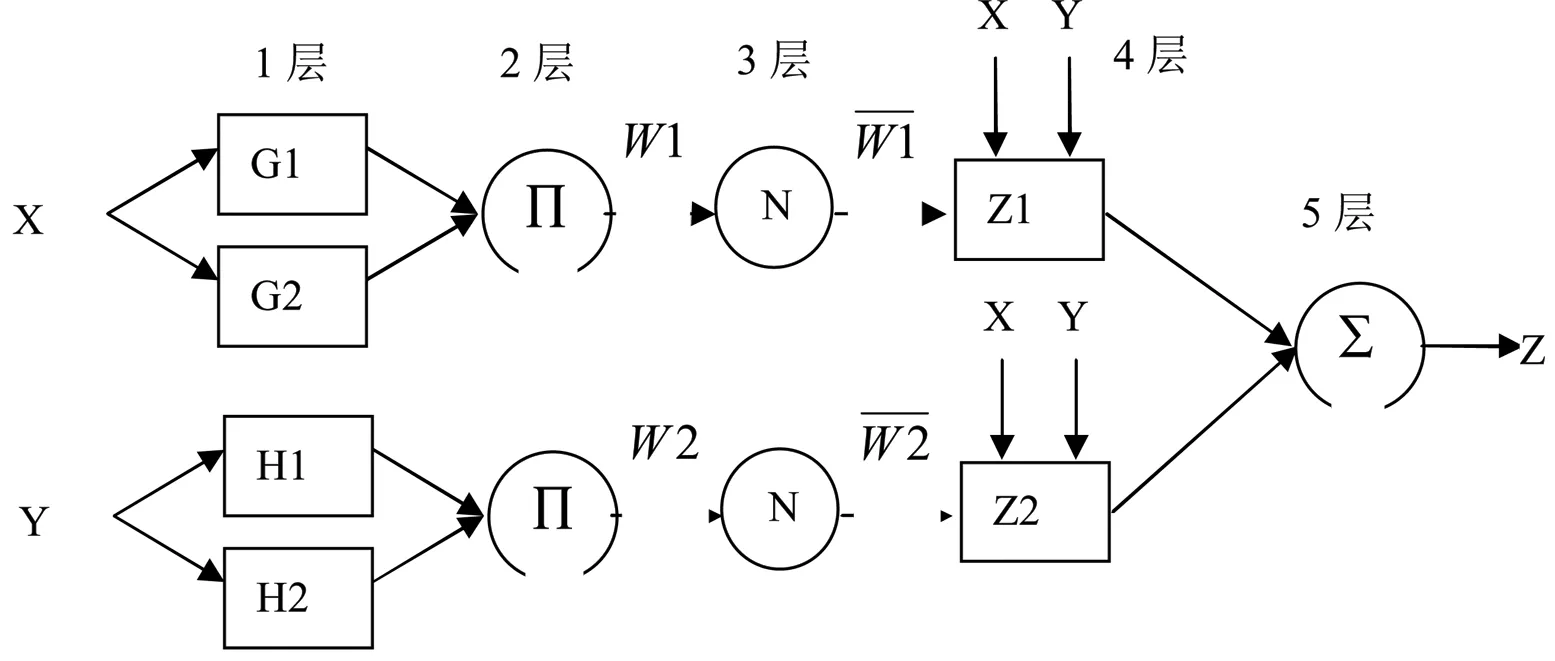
圖1Sugeno模糊系統的ANFIS結構

把ANFIS結構分成五層：

第1層：計算輸入變量的模糊隸屬度函數

O1,i=gxi(x,ai,bi),i=1,2

O1,j=gy(j-2)(y,cj-2,bj-2),j=3,4

其中O1,i的下標表示第1層輸出的第i個。

第2層：計算適用度。

O2,1=O1,1×O1,3=gx1(x,a1,b1)×gy1(y,c1,d1)記為W1

O2,2=O1,2×O1,4=gx2(x,a2,b2)×gy2(y,c2,d2)記為W2

第3層：歸一化適用度。

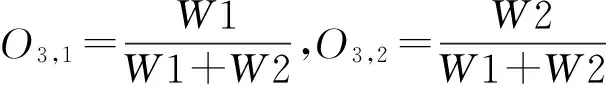
第4層：分別算出每條規則的響應。

Zi=pix+qiy+rii=1,2

第5層：最后計算模糊系統的輸出量。

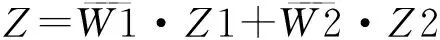
二、ANFIS應用于語音去噪中的基本原理

噪聲是一個隨機信號，而隨機過程是用功率譜密度函數表征的，功率譜密度函數的形態數值可以決定噪聲的“顏色”。 整個時域內功率譜密度函數為一常數，則顏色為“白色”，即“白噪聲”。功率譜密度函數不為常數噪聲稱為“有色噪聲”。日常生活中大多數的噪聲，比如電風扇的噪聲、汽車的噪聲、周圍工地施工的噪聲等，其頻譜主要集中在非白色的低頻段，屬于有色噪聲。白噪聲通過非線性動態之后可以構成有色噪聲，一般測量信號就是有用信號和有色噪聲的混合。信號濾波的主要目的就是消除噪聲獲得有用信號。使用ANFIS動態建模，非線性逼近有色噪聲，去除測量信號中的有色噪聲部分，最終得到有用信號。利用ANFIS對噪聲進行剔除的原理框圖如圖2所示。

圖中有用信號用s(k)表示，噪聲源用n(k)和n(k-1)表示，有色噪聲是噪聲源通過非線性函數獲得d(k)=f(n(k),n(k-1))，測量信號是有用信號和有色噪聲之和，即x(k)=s(k)+d(k)，ANFIS主要任務是對有色噪聲d(k)進行逼近復現得到d(k)′，它的輸入是噪聲源n(k)和n(k-1)，訓練數據中的輸出是逼近的有色噪聲d(k)′，在測量信號中去掉逼近的有色噪聲，獲得估計信號s(k)′，即s(k)′=x(k)+d(k)′。估計信號s(k)′和原有用信號s(k)越逼近，說明ANFIS的效果越好。

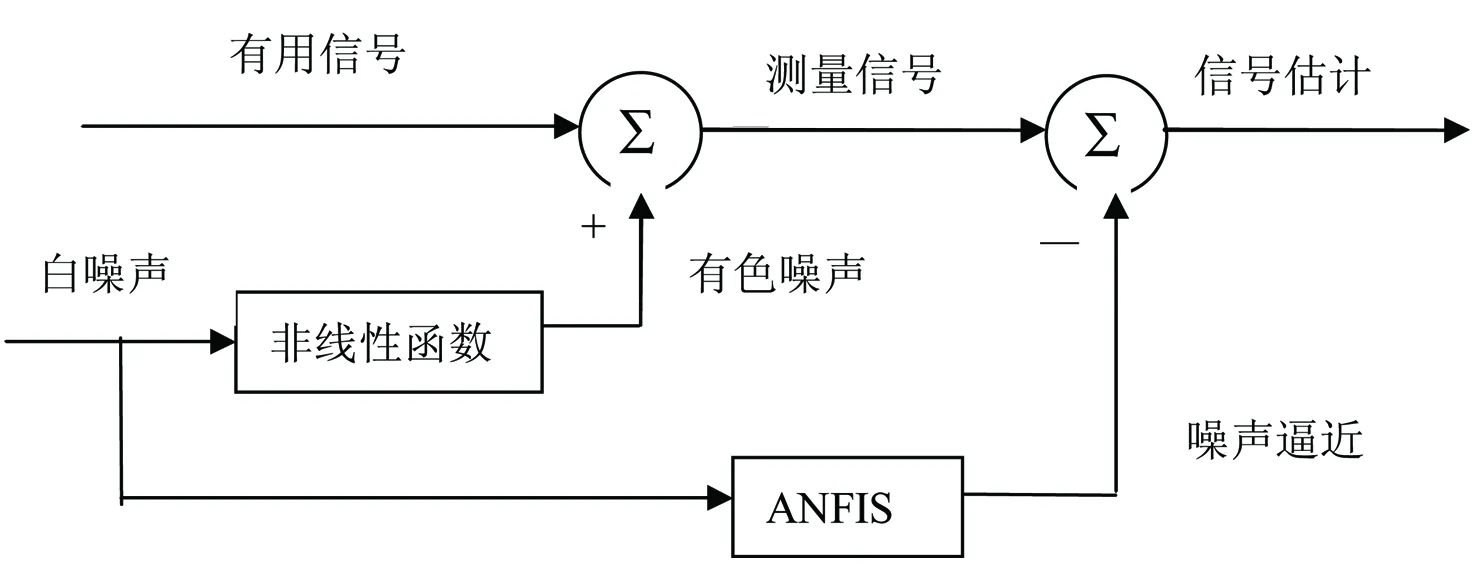
圖2　噪聲消除的基本原理

三、仿真實例

仿真1：從時域角度研究模糊理論檢測測量信號中的有用信號

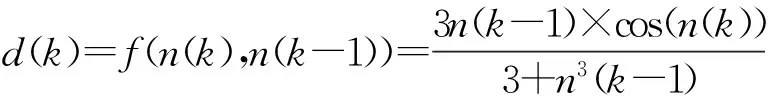
圖3 　(a)測量信號

圖3 　(b)噪聲的ANFIS逼近

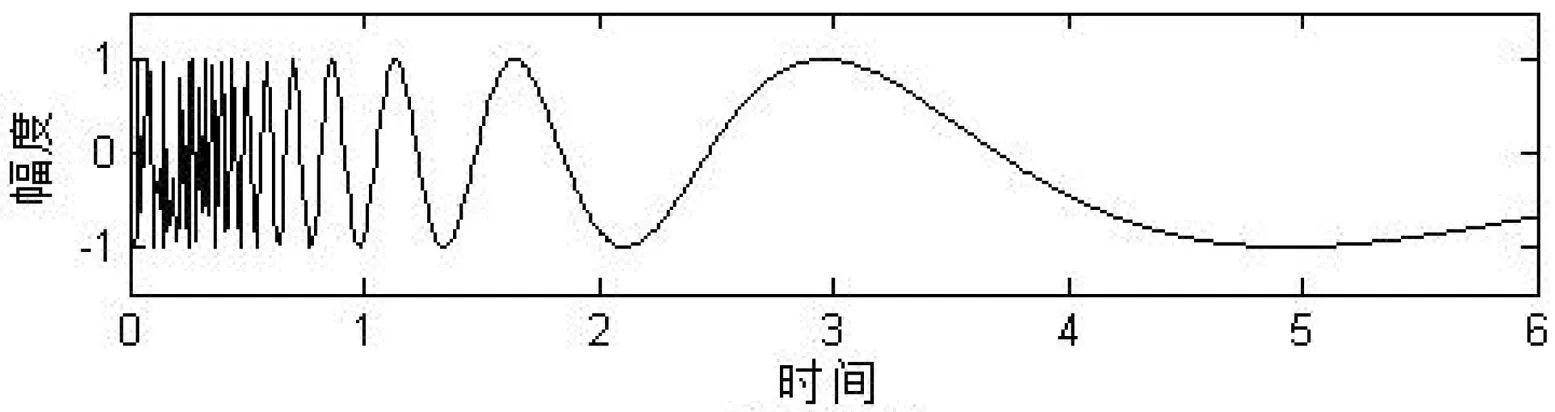
圖4 　(a)有用信號

圖4 　 (b)信號估計

圖3(a)是測量信號x(k)，可以看出有用信號已經淹沒在有色噪聲中，看不出明顯特征了。圖3(b)是噪聲的模糊逼近d(k)′。估計的有用信號

s(k)′=x(k)+d(k)′如圖4(b)所示，圖4(a)的原有用信號s(k)和圖4(b)估計的有用信號s(k)′從輪廓上已經十分逼近。說明ANFIS用于語音去噪的效果較好。

仿真2：從頻域角度研究模糊理論檢測測量信號中的有用信號

假如原有用信號包含兩個頻率分量：

s(t)=4sin(2πt)+7cos(7πt)

有色噪聲是白噪聲經過非線性函數f(k)之后得到，即：

其中n(t)表示白噪聲，n(n-1)是n(t)的前一時刻數值，測量信號為

x(t)=s(t)+d(t)

要求從測量信號中逼近出原有用信號。

圖5(a)信號

圖5(b)有色噪聲

圖5 (c)測量信號

圖5(a)中，有用信號是一個復合的周期信號，圖5(b)有色噪聲是將白噪聲通過非線性系統后得到的，圖5(c)測量信號是把有用信號加入有色噪聲的波形。可以看出有色噪聲對原信號的干擾很大，有用信號已經淹沒在噪聲中。

圖6　(a)信號

圖6　 (b)測量信號

圖6　(c)噪聲的模糊逼近

圖6 (d)信號估計

圖6(c)中，白噪聲經過自適應神經模糊推理系統(ANFIS)得到噪聲的模糊逼近，近似有色噪聲，把噪聲的模糊逼近從測量信號中剔除，得到圖6(d)信號估計。可以看出估計的信號與原信號圖6(a)相對比，基本輪廓十分相似，表明ANFIS成功對非線性動態進行了建模，但是仍有一些高頻毛刺，基本恢復效果較好。

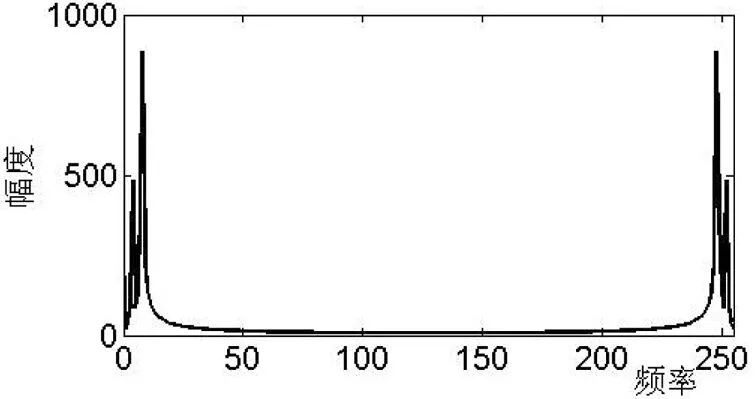
圖7(a)信號的頻譜

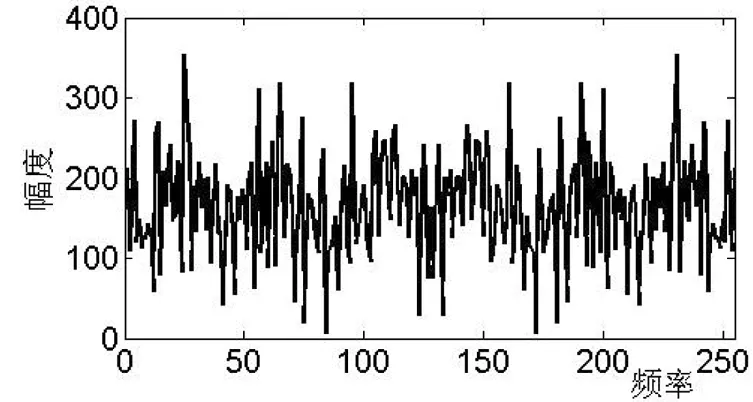
圖7(b)有色噪聲的頻譜

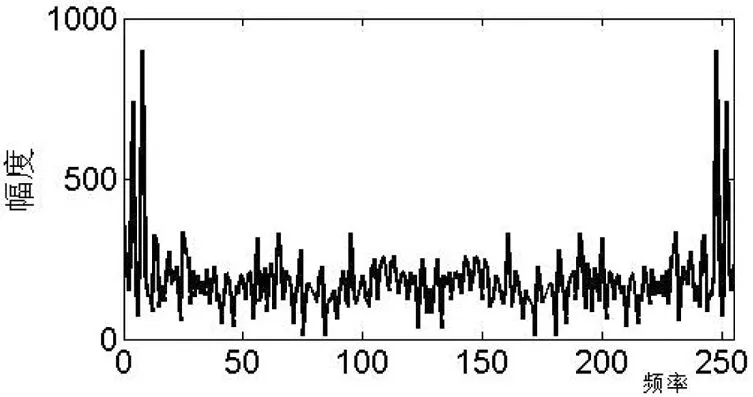
圖7(c)測量信號的頻譜

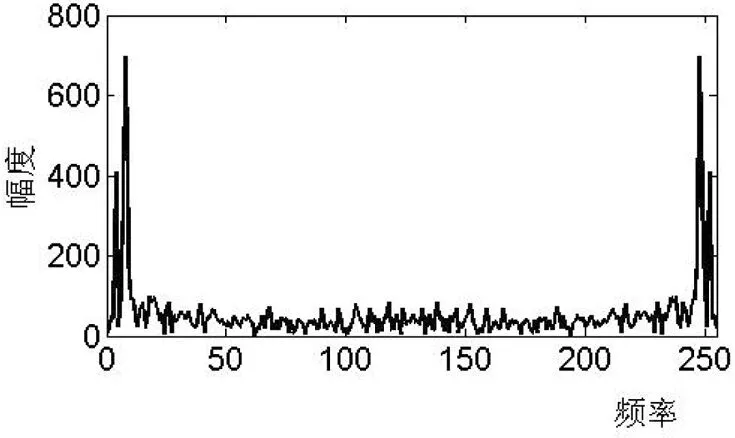
圖7(d)信號估計的頻譜

圖7中，把原信號的頻譜圖7(a)中混入有色噪聲頻譜圖7(b)，得到測量信號頻譜圖7(c)。從使用ANFIS得到信號估計頻譜圖7(d)中可以看出，比測量信號中的干擾減少了很多，取得了一定的效果。原信號和信號估計的頻率相比較，這兩者十分相似，但是在估計信號里面包括部分高頻分量，如果能再通過低通濾波器，那么恢復質量更高。

四、結語

自適應神經模糊推理系統(ANFIS)是在結合了神經網絡和模糊理論的基礎上發展起來的，克服了二者的確定。把ANFIS應用于信號去噪中，從仿真實驗中可以看出，從混入有色噪聲的測量信號中剔除噪聲，得到估計信號，取得了較好的還原效果。

參考文獻：

[1]曹國強,徐堃. 自適應神經模糊推理系統在脈沖電解加工中的應用研究[J]. 機械工程師,2016,(1):67～69.

[2]羅海馳, 李岳陽, 孫俊. 一種基于自適應神經模糊推理系統的圖像濾波方法[J]. 計算機科學,2013,(7):302～306.

[3]王艷永, 鄧方, 孫健. 改進的自適應神經模糊推理系統的角度傳感器誤差補償方法[J]. 控制理論與應用,2013,(10):1 342～1 346.

[4]秦炎峰,陳鐵軍. 自適應神經模糊推理系統的參數優化方法[J]. 微計算機信息,2008,(18):222～224.

[5]董小麗. 基于云模型的自適應神經模糊推理系統的裝備保障態勢評估方法的研究[D]. 蘭州：蘭州大學,2015.

[6]孫川川. 基于自適應神經模糊推理系統的離心式壓縮機建模[D]. 銀川：寧夏大學,2014.

[7]張浩炯，余岳峰，王強. 應用自適應神經模糊推理系統(ANFIS)進行建模與仿真[J]. 計算機仿真，2002，19(4):47～49.

[8]顧秀萍. 自適應神經模糊推理系統(ANFIS)及其仿真[J]. 火力與指揮控制,2010,35(2)：48～53.

文章編號：2095-4654(2016)04-0009-03

收稿日期：2016-01-05

基金項目：運城學院教學改革研究項目(JG201409)

中圖分類號：TN912.3

文獻標識碼：A