基于信息擴散理論的塵肺病風險評估研究

束堯宸,邵　輝,李　展,趙　旭

(常州大學環境與安全工程學院,江蘇 常州 213164)

?

基于信息擴散理論的塵肺病風險評估研究

束堯宸,邵輝,李展,趙旭

(常州大學環境與安全工程學院,江蘇 常州 213164)

摘要：在進行塵肺病職業危害風險評估時，由于相關信息獲得難度大、樣本數量少，傳統的統計模型基本上無法滿足風險分析的需求。基于信息擴散原理，通過擴散函數對不完備信息進行適當的擴充，建立起觀測樣本和風險概率分布的映射關系，構建了評估區域塵肺病風險分析模型，并利用某省2009—2013年新發塵肺病病例數以及新增的Ⅰ、Ⅱ、Ⅲ期塵肺病病例數作為塵肺病風險分析樣本，應用構建的塵肺病風險分析模型，對上述各類塵肺病的潛在風險進行評估，以為塵肺病預防和治理提供依據。

關鍵詞：塵肺病；信息擴散理論；職業危害；風險評估

塵肺病已經成為職業病中影響最嚴重的一種職業危害，每年罹患塵肺病的人數居高不下。現階段對于塵肺病的研究大多處于理論探究、監測與數值模擬相結合等方式[1-9]，然而區域內罹患塵肺病是小樣本事件，想要預測粉塵的潛在職業危害性，事先給出一個合理的統計模型進行風險評估幾乎是不可能的。以信息分配和信息擴散為核心的模糊信息優化處理技術是一門新興的數據處理技術，可以彌補樣本信息不足的缺陷，但目前信息擴散技術大多數應用于自然災害風險評估等方面，與職業危害方面相結合的研究并不多。本文基于信息擴散理論，根據某省2009—2013年塵肺病的統計數據，通過構建塵肺病風險分析模型，綜合分析出該區域內塵肺病的潛在危害性，并對其風險進行了評估，以為塵肺病預防和治理提供依據。

1信息擴散的定義

定義1：令X={x1,x2,…,xn}是一個隨機樣本，令U代表隨機變量X所有可能值的集，稱為X的論域，即U是隨機變量X的定義域。X和U分別簡稱為樣本和論域[10]。

定義2：令X是一個樣本，V是論域U的一個子集，從X×V到[0,1]的一個映射為

μ:X×V→[0,1]

(1)

(2)

稱為X在V上的一個信息擴散，如果它是遞減的，即

?x∈X,?v′,v″∈V

(3)

如果‖v′-x‖≤‖v″-x‖，則μ(x,v′)≥μ(x,v″).μ稱為一個擴散函數，簡稱為擴散，V稱為一個監控空間。由此我們得到：一個分配函數是一個擴散函數。

定義3：μ(x,u)是守恒的，當且僅當?x∈X，在其論域U上的積分值是1，即

∫Uμ(x,u)du=1

(4)

如果隨機變量的定義域U是離散的，U={u1,u2,…,um}，則守恒條件為

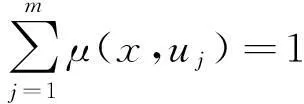
(5)

2基于信息擴散理論的塵肺病風險分析模型的建立

信息擴散是一種為了彌補信息不足，通過優化利用小樣本信息，并對樣本進行集值化模糊數學處理的方法，該方法可以將少量的觀測值樣本，擴散為一個模糊集，即把單值樣本變成集值樣本。根據信息擴散原理，在一個封閉系統中，信息擴散函數是遞減的，也就是說信息是沿著濃度減小的方向來移動。分子的自然擴散和信息擴散都具有填補空白的功能，并且都是沿著濃度減小的方向進行，因此當信息擴散不借助任何中介時，可以認為信息擴散過程遵循分子擴散過程的菲克第一定律和菲克第二定律[11-14]。在這個前提下，可得信息擴散過程的正態擴散函數f(ui)為

(6)

式中：h為正態擴散的擴散系數，該擴散系數是在研究正態擴散的擇近原則時人為提出的參數，其取值方式是根據黃金分割法推導得出的，在《自然災害風險評價理論與實踐》[10]一書中對其有詳細的推導過程，由于篇幅所限在此不予證明，直接運用即可。

設Y={y1,y2,…,ym}為觀測樣本集合，是風險因素在n年里的實際觀測值的集合，指標論域U={u1,u2,…,un}。

根據式(6)，第j個樣本的擴散函數可寫為fj(ui)，即

(7)

式中：fj(ui)為第j個樣本的擴散函數(j=1,2,…,m；i=1,2,…,n)。

令

(8)

相應的模糊子集的隸屬函數為

(9)

式(9)稱為樣本的信息歸一化分布，通過對其進行處理，可以得到一種較好的風險評估結果，即令

(10)

式(10)的物理意義是：由觀測樣本集合Y={y1,y2,…,ym}，經信息擴散推斷出，如果職業病觀測值只能取u1,u2,…,un中的一個，那么在將yj均看作是樣本代表時，觀測值為ui的樣本個數為q(ui)個。顯然，該值通常是一個正整數，但一定是個不小于0的數字，令

(11)

式(11)就是樣本落在ui處的頻率值，可以作為概率估計值。超過ui的概率估計值，即為超越概率p(u≥ui)，有

(12)

式(12)就是職業病風險估計值。

3實例應用與分析

3.1塵肺病風險分析數據的調查統計

某省以冶金、電子、機械等行業作為支柱產業，近幾年塵肺病在該省份表現較為顯著。該區域塵肺病按其嚴重程度可以劃分為Ⅰ、Ⅱ、Ⅲ期，本文遂以該區域內的塵肺職業病風險作為研究對象，在調研了大量的數據記錄以及相關的資料的情況下，以該省2009—2013年新發塵肺病病例數為樣本，統計分析出這五年該區域新發塵肺病病例數以及Ⅰ、Ⅱ、Ⅲ期塵肺病病例數，詳見表1。

3.2塵肺病風險分析觀測樣本的建立

區域內的塵肺職業危害風險評估是一個極其復雜的系統工程，涉及的因素多、變化大，可以利用的信息較少，因此本文采用信息擴散理論構建一個基于小樣本的區域塵肺病風險評估模型。根據表1統計得到的數據，建立了4個觀測樣本，即新發塵肺病病例數和Ⅰ、Ⅱ、Ⅲ期新增塵肺病病例數，這4個樣本分別為Y1、Y2、Y3、Y4，記為： Y1={760,1 120,753,803,615}；Y2={623,982,632,663,498}；Y3={102,89,70,95,76}；Y4={35,49,51,45,41}。

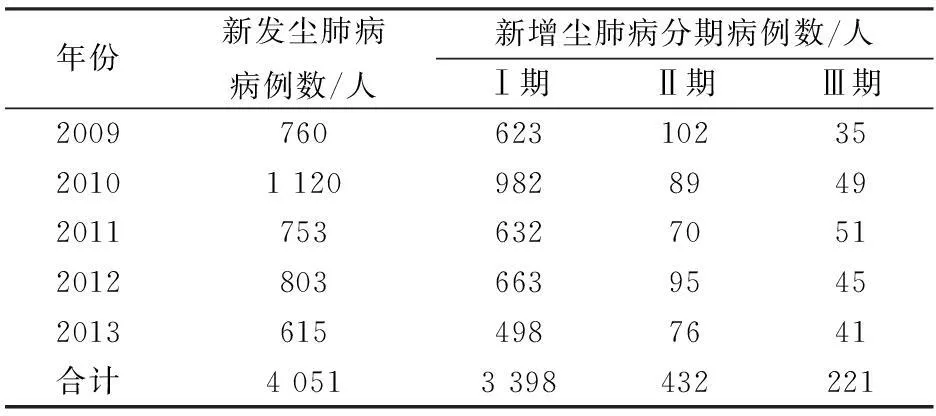
表1　某省2009—2013年新發塵肺病病例數

指標論域是根據觀測樣本數值的大小建立的，以包含所有觀測樣本。危險等級(步長)的設定并沒有特定的標準，在此要使觀測樣本點盡量多地落在控制點附近，以適當簡化計算工作量。

根據樣本Y1，確定指標論域U1[0,1 200]，取步長150，控制點{0,150,300,450,600,750,900,1 050,1 200}共9個，劃分9個風險水平；同理，根據樣本Y2，確定指標論域U2[0,1 000]，取步長100，控制點{0,100,200,300,400,500,600,700,800,900,1 000}共11個，劃分11個風險水平；根據樣本Y3，確定指標論域U3[0,105]，取步長15，控制點{0,15,30,45,60,75,90,105}共8個，劃分8個風險水平；根據樣本Y4，確定指標論域U4[0,60]，取步長10，控制點{0,10,20,30,40,50,60}共7個，劃分7個風險水平。

3.3擴散系數h的取值

根據樣本數據,可以進一步得到擴散系數h的取值，見表2。

表2　擴散系數的取值

注：表中n表示樣本容量；a表示樣本觀測值中的最小值；b表示樣本觀測值中的最大值；h為擴散系數。

樣本Y1的擴散系數h1：樣本容量為5，樣本觀測值中最大值為1 120 ，最小值為615，根據表2計算，h1=0.814 6×(1 120-615)=411.373；同理,樣本Y2的擴散系數h2：樣本容量為5，樣本觀測值中最大值為982，最小值為498，h2=0.814 6×(982-498)=394.27；樣本Y3的擴散系數h3：樣本容量為5，樣本觀測值中最大值為102，最小值為70，h3=0.814 6×(102-70)=26.07；樣本Y4的擴散系數h4：樣本容量為5，樣本觀測值中最大值為51，最小值為35，h4=0.814 6×(51-35)=13.033 6。

3.4模糊隸屬函數計算

根據公式(7)至(9),可得到4個樣本對應的模糊隸屬函數如下：

3.5塵肺病風險概率和超越概率的確定

根據樣本(這五年來新患塵肺病人的數量)，可計算出2009—2013年新發塵肺病不同的風險等級及其所對應的概率和超越概率，其計算結果見表3。

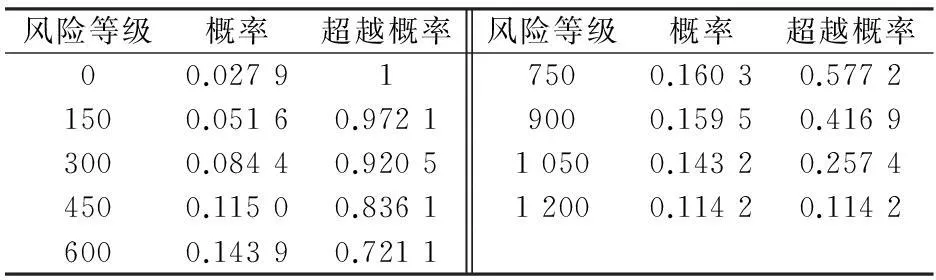
表3　2009—2013年新發塵肺病不同的風險等級及其

根據樣本Y2，可計算出2009—2013年新增Ⅰ期塵肺病風險等級及其所對應的概率和超越概率，其計算結果見表4。

表4　2009—2013年新增Ⅰ期塵肺病風險等級及其

根據樣本Y3，可計算出2009—2013年新增Ⅱ期塵肺病風險等級及其所對應的概率和超越概率，其計算結果見表5。

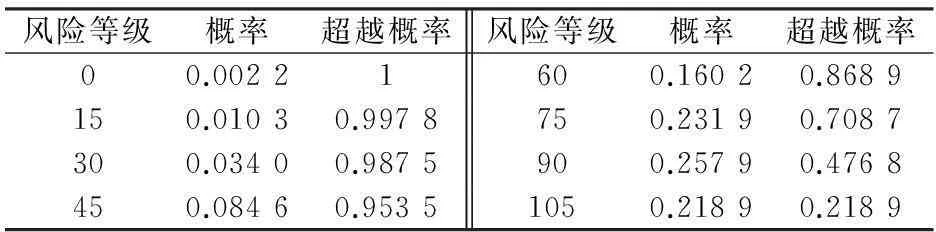
表5　2009—2013年新增Ⅱ期塵肺病風險等級及其

根據樣本Y4，可計算出2009—2013年新增Ⅲ期塵肺病風險等級及其對應的概率和超越概率，其計算結果見表6。

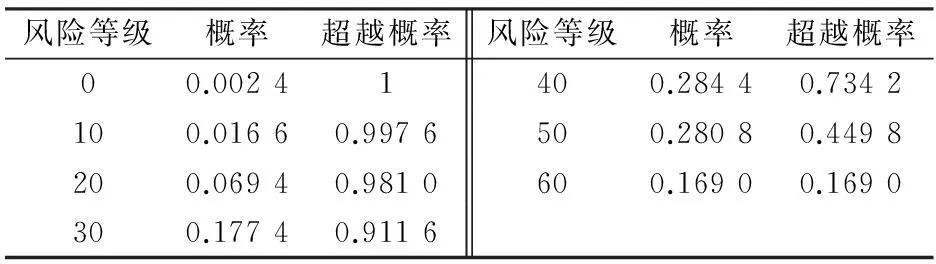
表6　2009—2013年新增Ⅲ期塵肺病風險等級及其

3.6結果分析

根據表3至表6，可得到該省近五年塵肺病的發生概率隨其風險(危害)等級的變化規律，見圖1至圖4。

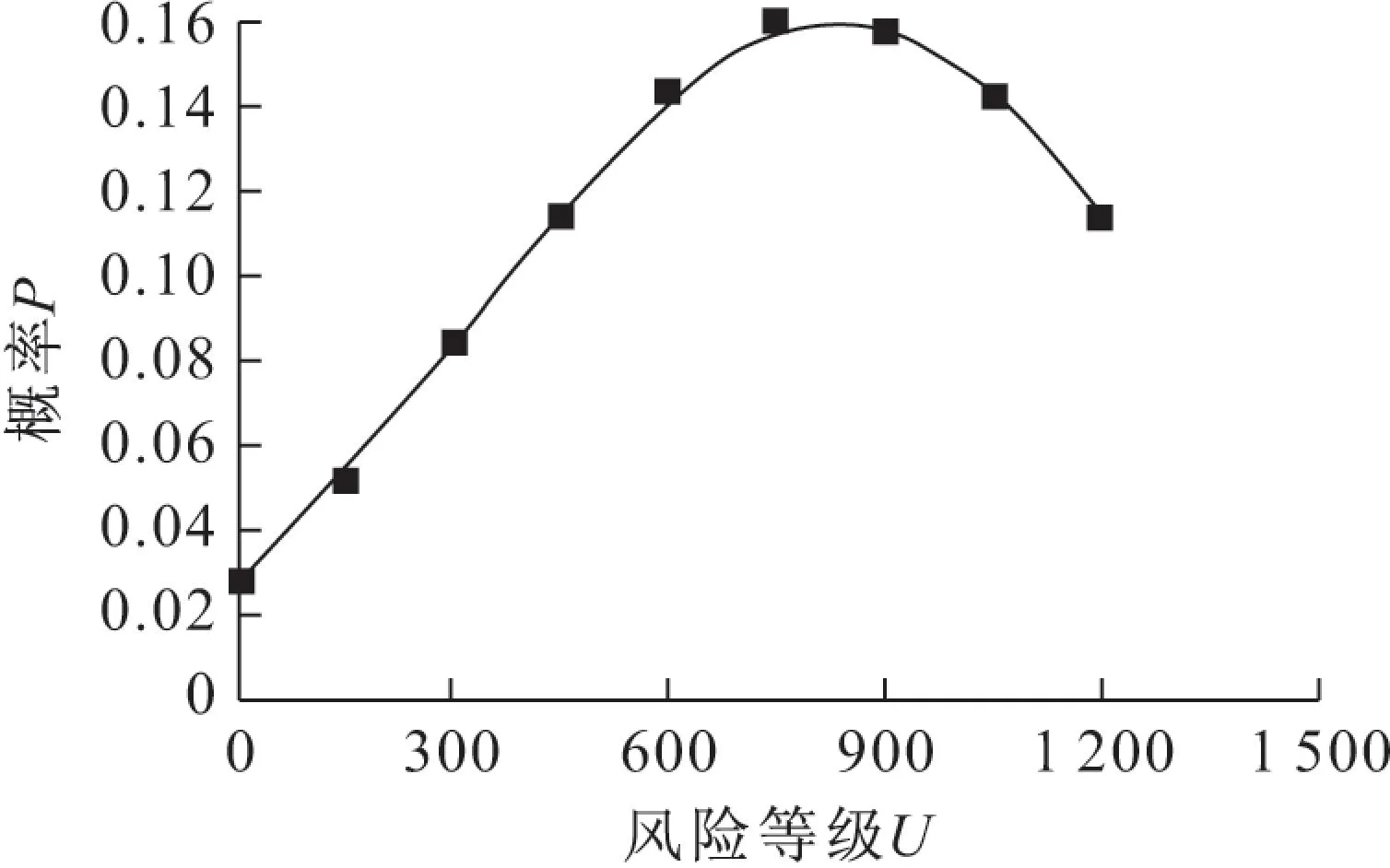
圖1　新發塵肺病的風險等級和概率分布圖Fig.1　Risk levels and probability distribution of the　　　newly diagnosed pneumoconiosis

圖2　新增Ⅰ期塵肺病的風險等級和概率分布圖Fig.2　Risk levels and probability distribution of the　　　newly diagnosed phase I pneumoconiosis

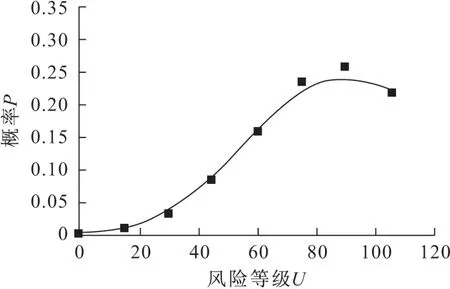
圖3　新增Ⅱ期塵肺病風險等級和概率分布圖Fig.3　Risk levels and probability distribution of the　　　newly diagnosed phase II pneumoconiosis

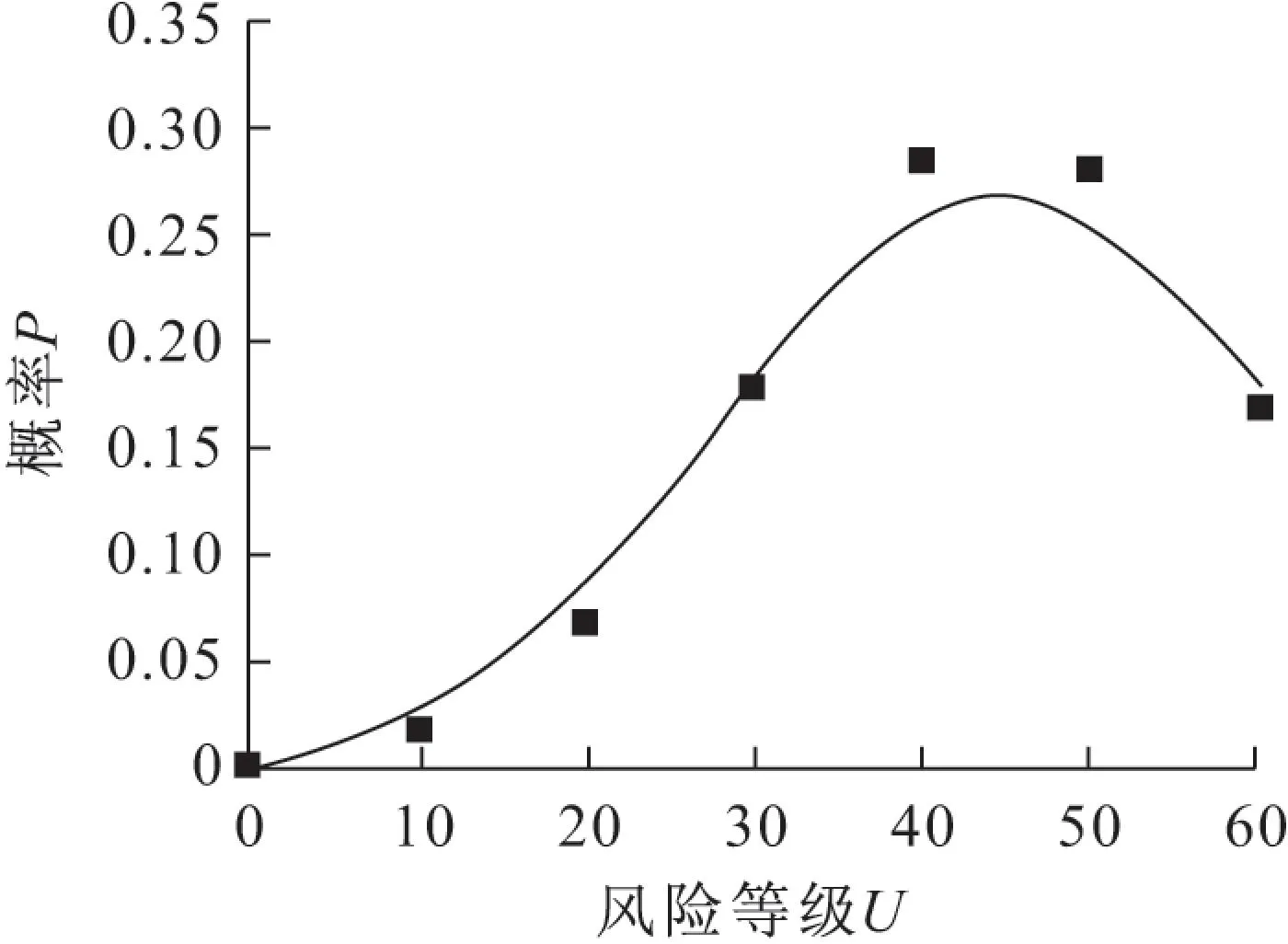
圖4　新增Ⅲ期塵肺病風險等級和概率分布圖Fig.4　Risk levels and probability distribution of the　　　newly diagnosed phase III pneumoconiosis

由圖1至圖4可見，該省新發塵肺病總人數以及新增Ⅰ、Ⅱ、Ⅲ期塵肺病的發生概率隨著其風險等級的上升均呈現出先上升后下降的趨勢。具體來看，圖1顯示出該省每年新發塵肺病Y1總人數在風險等級為450～1 200人之間的概率都在11%以上，在750～900人之間的概率達到了峰值，在1 200人左右其概率依舊維持在一個較高的水平上，因此應該注重控制新發塵肺病總人數，并通過相關措施將新發塵肺病人數控制在一個可接受的范圍內；圖2顯示出新增Ⅰ期塵肺病Y2病例人數在300～1 000人之間的概率達到了10%以上，在700人時的概率達到了峰值12.3%，由此看出新增Ⅰ期塵肺病病例人數在將來很大程度上將保持近幾年來的趨勢；圖3則說明了風險等級較高時，新增Ⅱ期塵肺病Y3病例人數的概率也偏大，新增Ⅱ期塵肺病病例人數在風險等級為60～110人之間的概率在15%以上，在90人左右時的概率達到了峰值25.7%;圖4則說明了新增Ⅲ期塵肺病Y4病例人數在風險等級為40～50人之間的概率最高，達到了將近30%，由于Ⅲ期塵肺病的危害程度最高，因此應該將新發Ⅲ期塵肺病病例人數控制在一個合理的可接受范圍內。

本文將計算得到4組超越概率繪制成曲線，該省近五年的塵肺病職業危害以及新增Ⅰ、Ⅱ、Ⅲ期塵肺病風險等級與超越概率的關系見圖5和圖6。

由圖5可見，該省新發塵肺病Y1的風險估計值隨著風險水平的增大而減小，每年新增塵肺病總人數在750人左右的概率為57.72%，在1 200人時的概率為11.42%；每年新增Ⅰ期塵肺病Y2風險估計值隨著風險水平的增大而減小，新增Ⅰ期塵肺病病例人數在0～600人之間的概率達到了55.66%，在900人以上的概率較小，約為20.45%。

由圖6可見，該省新增Ⅱ期塵肺病Y3的風險估計值隨著風險水平的增大而減小，每年新增Ⅱ期塵肺病病例人數在0～75人之間的概率達到了70.87%，而在105人左右的概率為21.89%;新增Ⅲ期塵肺病Y4的風險估計值也是隨著風險水平的增大而降低，每年新增Ⅲ期塵肺病病例人數在0～40人之間的概率達到了73.42%，在60人左右的概率為16.9%。

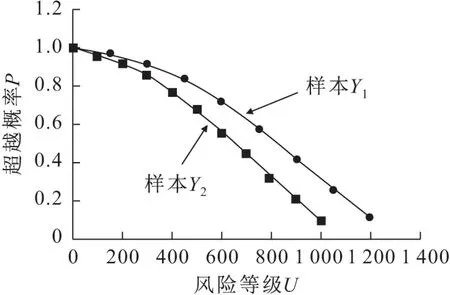
圖5　新發塵肺病和新增Ⅰ期塵肺病風險等級和超越　　　概率分布圖Fig.5　Risk levels and exceedance probability　　　distributions of the newly diagnosed and　　　phase I pneumoconiosis

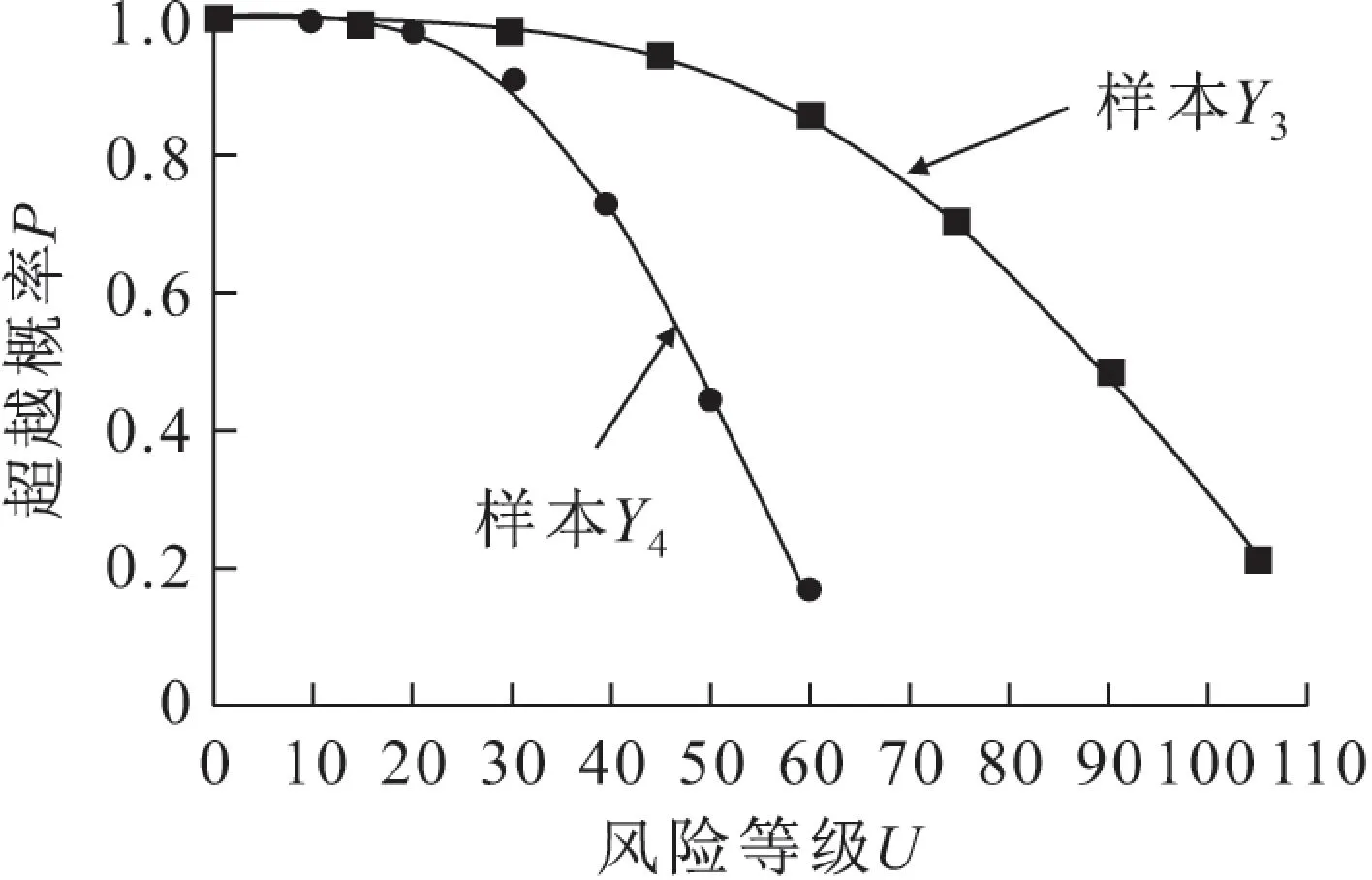
圖6　新增Ⅱ、Ⅲ期塵肺病風險等級和超越概率分布圖Fig.6　Risk levels and exceedance probability　　　distributions of the newly diagnosed and　　　phase Ⅱand Ⅲ pneumoconiosis

由此可見，該省近五年塵肺病的發病現狀與通過信息擴散理論構建的數學模型所計算得到的結果保持了高度的一致性，基本符合實際情況。根據計算得到的結果，該省每年有50%以上的可能性產生750例左右的新發塵肺病患者，Ⅰ、Ⅱ、Ⅲ期塵肺病患的新增病例人數在600人、75人、40人這三個風險等級上的概率都在50%以上，說明這三類新增塵肺病均處于一個較高的水平，特別是Ⅱ、Ⅲ期塵肺病為更為嚴重的塵肺病,因此這就提示我們要注重作業現場的粉塵控制，加強相關部門的監管力度，做好除塵防塵措施以及為相應的人員配備防塵用品等工作，把塵肺病風險降至最低水平，以確保作業人員的生命健康和安全。

4結論

(1) 基于區域內的塵肺病病例是小樣本事件，要對區域內的塵肺病風險進行評估，現有的統計模型并不能滿足風險分析的需求，因此本文嘗試將職業衛生問題和信息擴散方法相結合，對樣本點進行集值化處理，將信息擴散方法延伸到了職業衛生問題，構建了評估區域塵肺病風險的分析模型。

(2) 利用某省2009—2013年間的塵肺病統計資料，應用構建的塵肺病風險分析模型對該區域內的塵肺病風險進行了評估，結果表明：評估結果與實際情況基本保持一致，可以為該省的粉塵防治與控制提供參考。

(3) 應用結果證明將信息擴散方法與職業衛生問題相結合是切實可行的，但是論域、步長的選擇和風險等級的劃分對于結果產生的影響以及步長的設置是否具有特定的標準還有待進一步的研究。

參考文獻：

[1] 張忠彬.作業場所職業危害風險綜合評價研究[J].中國安全生產科學技術,2010,6(4):124-127.

[2] 馬超.作業環境中粉塵的危害、傳播機理和防治措施[J].安防科技,2011(2):57-59.

[3] 李明,吳超.粉塵點污染擴散模型的可視化研究[J].環境科學與技術,2006，11(29):12-14.

[4] 魏宗蘇,魏傳光,金龍哲.全工班呼吸性粉塵測定及防塵措施研究[J].中國安全科學學報,2008，18(9):106-110.

[5]HuXM,WangB,FanBB.ResearchonKMC-basedevolutionsimulationofdustparticlesinvirtualcampusenvironment[J].Simulation Modelling Practice and Theory,2014,40:28-38.

[6]XuZ,TravisJR,BreitungW,etal.Verificationofadusttransportmodelagainsttheoreticalsolutionsinmultidimensionaladvectiondiffusionproblems[J].Fusion Engineering and Design,2010,85:1935-1940.

[7]QinY,WangT,ChenY,etal.Investigationandponderingofdustandpoisonhazardsin44smallwoodenfurnitureenterprises[J].Procedia Engineering,2012,43:484-488.

[8]DatsonH,HallD,BirchB.Validationofanewmethodfordirectionaldustmonitoring[J].Atmospheric Environment,2012,50:1-8.

[9]KhalajiM,RoshanzadehB,MansooriA,etal.Continuousdustmonitoringandanalysisbysparkinducedbreakdownspectroscopy[J].Optics and Lasers in Engineering,2012，50:110-113.

[10]黃崇福.自然災害風險評價[M].北京:科學出版社,2005.

[11]邵輝,朱岳清,邵峰.基于信息擴散的城市區域風險研究[J].中國安全科學學報,2011，21(5):166-170.

[12]楊旭,李春晨.基于信息擴散理論的火災風險評估模型研究及其應用[J].工業安全與環保， 2010，36(1):42-43.

[13]劉桂友,徐琳瑜.一種區域環境風險評價方法—信息擴散法[J].環境科學學報,2007，27(9):1549-2556.

[14]王洪德,鄭玉錢.基于網格劃分及信息擴散的化工園區安全風險評價技術[J].系統工程理論與實踐,2010，30(7):1286-1292.

[15]鄭雙忠,鄧云峰,蔣清華.基于火災統計災情數據的城市火災風險分析[J].中國安全生產科學技術,2005，1(3):15-18.

Pneumoconiosis Risk Assessment Based on Information Diffusion Theory

SHU Yaochen,SHAO Hui,LI Zhan,ZHAO Xu

(SchoolofEnvironment&SafetyEngineering,ChangzhouUniversity,Changzhou213164,China)

Abstract:Due to the difficulty of acquiring relevant information and lack of samples in the occupational hazard risk evaluation of pneumoconiosis,traditional statistic models fail to meet the need for risk evaluation.Based on the principle of information diffusion,this paper uses spread function to extend the incomplete gathered information,establishes the mapping relationship between observation samples and risk probability distributions,and constructs the calculating model of risk evaluation of regional pneumoconiosis.By using the constructed model,the paper takes newly diagnosed pneumoconiosis patients and newly diagnosed phase I,II and III pneumoconiosis patients in a certain province from 2009—2013 as samples to evaluate the respective potential risk of above-mentioned pneumoconiosis,which provides reference for preventing and curing pneumoconiosis.

Key words:pneumoconiosis;information diffusion theory;occupational hazards;risk assessment

文章編號：1671-1556(2016)03-0030-06

收稿日期：2015-10-13修回日期：2016-02-01

基金項目：國家安全監管總局2013年安全生產重大事故防治關鍵技術科技項目[安監總廳科技(2013)140號]

作者簡介：束堯宸(1991—)，男，碩士研究生，主要研究方向為城市公共安全與職業衛生。E-mail:yaochenshu@126.com

中圖分類號：X18；R135

文獻標識碼：A

DOI：10.13578/j.cnki.issn.1671-1556.2016.03.005

通訊作者：邵輝(1955—)，男，教授，主要從事安全工程等方面的教學與研究工作。E-mail:hshao@cczu.edu.cn