感悟數形結合思想，強化思維策略

花修平

摘 要：隨著素質教育的不斷發展和教育體制的變革，教育行業不斷進步。而數學具有綜合性、復雜性和邏輯性的學科，影響著學生未來的擴散思維和邏輯思維能力的養成。在進行數學課程教學中，使用數形相結合的方式，有助于學生創新思維和觀念的養成，有助于提升數學課堂教學的質量和效率。在新課程改革不斷深入的背景下，人們對數學教學有了更高要求，因此，就要求教師在教學的過程中，要充分運用數形結合的思想，促進學生發展。本文就結合蘇教版初中數學教材，探究數形結合思想的優勢和運用方法。

關鍵詞：數形結合；初中數學；思維；戰略

隨著教育體制和社會的進步，社會對人才的要求越來越高，使得教育模式也隨之發生改變，由原有的應試教育改變成為素質教育。但是，在現階段初中數學教學的過程中，要求學生不但要全面地掌握知識，還要能夠將知識運用到實際生活中，所以，教師要改變原來的教學方法，融入數形思想，使學生對知識的理解和吸收更加深刻。通常情況下，數形結合教學模式，能夠在闡述知識時更具直觀性，它能夠把抽象的教材知識點轉化為圖像和圖形，從而使學生更準確、牢固地掌握知識。

一、“數形結合”概述

數形結合就是把抽象化、難以理解的數學語言轉變成為更加直觀的圖形，便于學生掌握和理解。從本質上說，就是把代數問題轉變為幾何問題。數形結合方法是對數學學科進行研究的關鍵方法，它能夠把抽象、復雜的代數和形象直觀的幾何結合起來，把形象直觀和抽象思維結合起來，使抽象的數學問題更加生動化和主觀化，把抽象的思維轉變為形象思維，能夠促進學生更好地掌握、理解數學問題。在初中數學階段使用數形結合的思想，有利于學生培養抽象性思維和數學邏輯思維。在數學教學中可以通過四個方面來開展：一是形成合適的代數模型，主要針對函數模型、不等式和方程問題；二是形成合適的函數圖像或是幾何模型，主要針對解決函數和方程問題；三是解決和函數相關的幾何綜合、代數等問題；四是使用圖像的形式把要解決的問題呈現出來。使用數形思想的關鍵點就在于要把握好形和數的關聯點。如果能夠有效地把點和形結合在一起，就可以使很多難題迎刃而解。另外，教師要讓學生在學習的過程中，使用綜合、概括、抽象、分析、觀察和類比，主動使用數形結合觀念。

二、數形結合的有效策略

1.以數化形方法

以數化形方法就是把代數問題中的條件及數量關系利用圖形表現出來，借助“圖形”的直觀性來探究數量關系，由數化形，數形結合，從而拓寬思路轉化思維方式，使難題變為易題，直觀、簡捷地找到解題途徑，這種思維策略體現了數形結合的數學思想的運用。

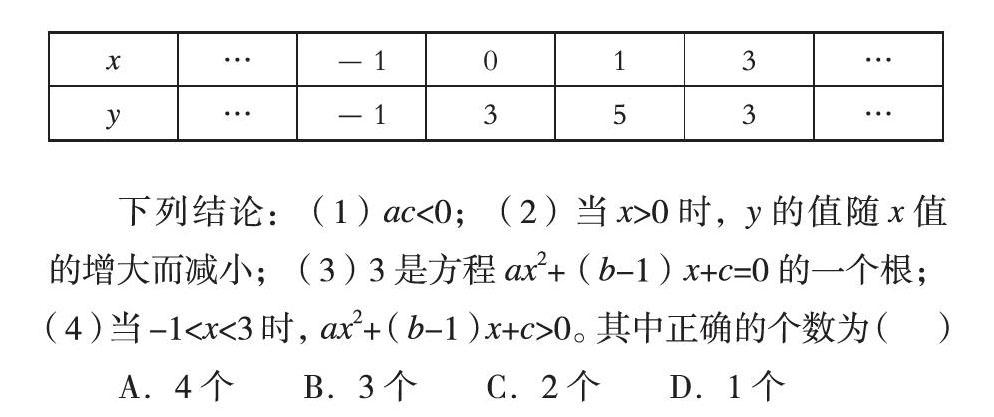
在數學教學中，這種思維策略要滲透給學生，在函數部分教學這一策略會經常用到。如下面這道題：二次函數y=ax2+bx+c（a，b，c為常數，且a≠0）中的x與y的部分對應值如表：

下列結論：（1）ac<0；（2）當x>0時，y的值隨x值的增大而減小；（3）3是方程ax2+（b-1）x+c=0的一個根；（4）當-10。其中正確的個數為（ ）

A.4個 B.3個 C.2個 D.1個

題目給出的數量關系是表格的形式，很多學生會根據數據求出二次函數的表達式后再去解決問題。實質上，從圖表的數據中我們可以觀察出，x從左向右在增大，而y的值先增大后減小，由此就可以確定拋物線開口方向是向下的，再根據對稱性就可以畫出拋物線的大致圖像。利用圖像解決問題能夠降低這道題目的難度，從而將一個看似復雜的問題輕松解決，這樣以數化形的策略把學生從問題困境中解救出來，也增強了學生學習數學的興趣和信心。

2.以形變數

以形變數就是把幾何問題中的變量用字母表示，用數量關系描述圖形性質，從而將幾何問題轉化成代數問題。這種思維策略體現了數形結合思想和方程函數思想。

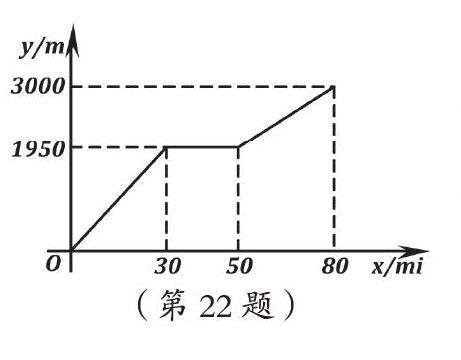
例如，某年南京中考數學的第22題，小穎和小亮上山游玩，小穎乘坐纜車，小亮步行，兩人相約在山頂的纜車終點匯合。已知小亮行走到纜車終點的路程是纜車到山頂的路線長的2倍，小穎在小亮出發后50min才乘上纜車，纜車的平均速度為180m/min。設小亮出發xmin后行走的路程為ym。圖中的折線表示小亮在整個行走的過程中y與x的函數關系。

小亮行走的總路程是多少，他途中休息了多長時間。

①當50≤x≤80時，求y與x的函數關系式。

②當小穎到達纜車終點時，小亮離纜車終點的路程是多少？

這是一道典型的數形結合題，題目中給了相應的圖像和數量關系，并要求學生根據圖像和數量關系進行分析，最后得出結論。根據題意我們可以得知，x、y分別代表一個變量，x代表的是小亮出發的時間，y代表的是小亮行走的路程，分析到這里，我們就可以直接得出第一小題的答案，從圖形中直接就可以看出，小亮行走的路程是3600米，中途30～50分鐘的時候，小亮的路程變化為0，由此得出，小亮的休息時間是20分鐘。這道題解答到這里，我們已經可以從圖像中得出這些內容，從而解答出第一題總路程為3600米，途中休息了20分鐘。

再來看第二小問，根據題意我們可以知道，50～80分鐘的時候，小亮行走的路程與時間之間的關系是一次函數的圖像的一部分，因而把（50，1950）、（80、3600）兩點的坐標代入一次函數的解析式，得出y與x的函數關系式，從而實現了以形變數的策略。

根據題中的文字描述我們可以知道，小亮行走的路程是小穎乘坐纜車行走的兩倍，由此可以得出小穎乘坐纜車行走的路程為1800米，由于纜車的平均速度為180m/分，所以小穎乘坐纜車到達終點所用的時間是10分鐘，由小穎在小亮出發后50分鐘才坐上纜車，對應于圖像，我們可以知道在小亮休息結束后，小穎又開始出發的，因而我們可以知道在小穎到達終點20分鐘之后，小亮又到達了終點，也就是在小亮出發60分鐘后，小穎就已經到達了終點。根據之前求出的x、y的函數表達式，可以將x=60帶入，最后求出y的值，用3600減去y的值，就可以得出答案。這道題進行到這里我們可以看出，將圖形轉化成數的能力也是非常重要的，縱觀幾年來的中考題和模擬題，有許多的題目都是根據數形結合的思想，要么將數轉化為形，要么將形轉化成數，無論是哪種轉化，都需要學生對數形結合的思想掌握地非常透徹。

三、數形結合的優勢

使用數形結合，能夠使學生解決疑難問題更具靈活性，使學生解決問題和分析問題的能力得以提升。在數學教學過程中，結合數形結合的思想，能夠讓學生更加理解數形結合是要找到形和數的關鍵點，再按照對象的屬性，把形和數有效地結合在一起，互相轉化，找到更為簡單的解題思路。

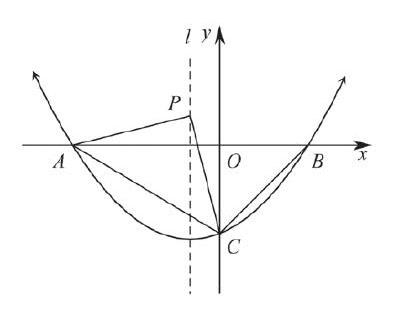
例如，2015年蘇州中考數學試卷第27題：如圖，已知二次函數y=x2+（1+m）x-m（其中0

本題主要考查了二次函數與幾何的綜合，以及勾股定理、相似三角形和二次函數最值求法等知識點。求P的坐標時，如果利用傳統的方法，過P點作PD⊥y軸于點D，根據勾股定理構造方程可以得到P點坐標，不過這種方法的計算量很大。若采用數形結合的思想，由拋物線的對稱性，得PB=PC，通過求BC的垂直平分線與拋物線對稱軸l的交點即可。同樣，在第3小題中需要證明∠ACP為直角，采用勾股定理的逆定理也是比較麻煩的。觀察幾何圖形不難發現點A、B、C在⊙P上，因為∠ABC=450，所以很快得到∠ACP=2∠ABC=900。對于這樣的中考壓軸題難度是可想而知的，解題時必須在充分利用幾何圖形的性質及題設的基礎上，挖掘幾何圖形中隱含的數量關系和位置關系，在復雜的“背景”下辨認、分解基本圖形，或通過添加輔助線補全或構造基本圖形，并善于聯想所學知識，突破思維障礙，借助數形結合思想簡化解題過程。

在教學過程中，教師要有意識地引導學生從不同角度去觀察問題，就有可能得出不同的思考過程和不同的解題方法。因此，教師應注重學生數學思想意識的培養，逐步訓練學生運用數學思想指導思維活動的能力，這樣能夠以量變促質變，從而優化解題過程，提高解題能力，并因此形成數學學習效果的廣泛遷移，實現思維策略的強化。

參考文獻：

[1]單淑娟.感悟數形結合歸納解題通法——“拋物線的變換”專題復習課的教學感悟[J].中學數學，2014（6）：25-26.

[2]焦劍.數學思想在教學中的感悟[J].東西南北·教育觀察，2011（5）：107.

[3]陳花.“感受數形結合思想的內在力量”的實踐與思考[J].教育界，2015（34）：122.

[4]竺忠燕.讓學生在活動中感悟數形結合的思想方法——“面積與代數恒等式”教學案例[J].中國科教創新導刊，2011（12）：120-121.

[5]徐林超.讓數學思想在課堂學習中獲得感悟[J].中學課程輔導·教學研究，2012，6（13）：9.