基于自助最大熵法的滾動軸承無失效數據可靠性評估

夏新濤，朱文換，孫立明，葉亮，邱明

(1. 河南科技大學 機電工程學院，河南 洛陽 471003；2. 洛陽軸研科技股份有限公司，河南 洛陽 471039)

為確保安全運行，試驗機、飛機、高鐵、汽車等機械系統對滾動軸承試驗或服役時期的可靠性要求越來越高[1]。在軸承試驗或服役過程中，由于諸多原因造成滾動軸承的性能指標達不到使用要求，使其產生疲勞、磨損、燒傷等失效，甚至發生惡性事故。因此，在軸承試驗或服役期間滾動軸承無失效時或者沒有發現失效時，應事先分析滾動軸承的無失效數據[2]，對滾動軸承的失效概率進行估計[3-6,13]，即根據滾動軸承的無失效數據對滾動軸承的可靠性進行預測。

目前，無失效數據可靠性評估采用的研究方法主要有經典統計學法和Bayes統計法，最常用的是Bayes統計法[2-10]，其前提是已知所研究滾動軸承壽命的概率分布，如對數正態分布[3]、指數分布[6]、Weibull分布[5,8-9]、二項分布、均勻分布等。而滾動軸承的多種失效導致了其概率分布未知，因此，現有方法對概率分布未知的滾動軸承壽命無失效數據可靠性的研究有一定的缺陷。

現融合自助法[11]和最大熵原理[12]，運用自助最大熵法，首先處理滾動軸承壽命試驗或服役過程中概率分布已知和未知時的無失效數據，然后構建壽命失效數據的可靠性函數，進而預測壽命失效數據可靠性的真值函數及其上下界函數，實現滾動軸承壽命無失效數據可靠性評估。

需要說明的是，提出的自助最大熵法是針對滾動軸承試驗或服役期間沒有發生任何失效時獲取的無失效數據，即所考察的無失效數據不同于定時截尾試驗中獲得的無失效數據。因此，自助最大熵法不適用于定時截尾試驗軸承均無失效的相同無失效數據的分析,定時截尾試驗中軸承均無失效時的情況需要進一步研究。

1 建立無失效數據可靠性模型

1.1 數據采集

假設滾動軸承無失效數據為隨機變量x，對其壽命無失效數據進行定期采樣，獲取原始數據，構成一個無失效數據序列X,

X=(x(1),x(2),…,x(n));

n=1,2,…,N，

(1)

式中：x(n)為第n個無失效數據；n為無失效數據的序號；N為無失效數據的個數。

1.2 數據生成

根據自助原理，通過自助再抽樣將原始無失效數據生成大量無失效數據。在進行自助抽樣前，需選定抽樣個數。首先令第1組選取的抽樣個數為L1，然后等間隔地選擇抽樣個數Li(i為抽樣個數的組號，一般取4～10)，直到Li=N為止；然后對抽樣個數不同的多組原始無失效數據分別進行自助再抽樣，根據自助原理從X中等概率可放回地進行抽樣，抽取n次，可得到一個自助樣本Xib，且其共有N個數據。連續重復抽取B次，得到B個自助再抽樣樣本，即大量無失效數據XB為

XB=(Xi1,Xi2,…Xib,…XiB);b=1,2,…,B,

(2)

Xib=(xib(1),xib(2),…,xib(n));

n=1,2,…，N,

式中：Xib為第i組自助樣本Xi的第b個自助樣本；B為第i組自助樣本XB的數據個數，一般取1 000～100 000；xib(n)表示自助樣本Xib中的第n個數據。

自助樣本Xib的均值為

(3)

1.3 預測數據的概率分布

根據最大熵原理，原始無失效數據生成的大量無失效數據應滿足最大熵準則。用最大熵法可以獲取大量無失效數據的概率分布的最好估計。

對于原始無失效數據生成的大量無失效數據，用一連續變量u來表示大量無失效數據序列XB中的自助樣本Xib，定義最大熵H(u)為

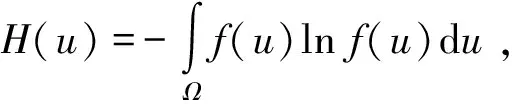
(4)

式中：f(u)為無失效數據的概率密度函數；Ω為變量u的積分區間。

(4) 式的約束條件為

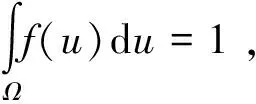
(5)

(6)

式中：m為所用原點矩的階數；mk為第k階原點矩。

根據 (2) 式可得無失效數據的各階原點矩為

(7)

令

H(u)→max ，

(8)

(9)

令

(10)

可得到

(11)

(12)

(13)

(14)

(14) 式為最大熵概率密度函數的解析式。

將(14)式代入 (5) 式可得

(15)

求解可得

(16)

(17)

將 (16) 、(17)式分別對λk進行微分可得

(18)

(19)

比較(18)式和(19)式，m階原點矩應滿足

(20)

通過(20)式可建立求解λ1,…,λk,…,λm的m個方程組，再由(18)式求出λ0，可得無失效數據的概率密度函數f(u)的解析式。

由f(u)解析式可得無失效數據的概率分布函數F(u)為

(21)

1.4 構建可靠性函數

定義一個有關滾動軸承壽命無失效數據個數的估計參數G(u)為

G(u)=N[1-F(u)]。

(22)

假設有關滾動軸承壽命的經驗失效概率分布函數P(u)為

(23)

式中：c為經驗概率系數，其取值會影響可靠性函數的計算結果。

當c為0.01～0.5時，c越小，可靠性函數的取值范圍越小；反之，可靠性函數的取值范圍越大[13]。在滾動軸承壽命試驗或服役過程中，假設無失效數據的取值區間是[xmin,xmax]=[x(1),x(N)]。根據現有的可靠性研究成果和工程實踐[7,13-14]，當壽命x的取值接近xmin時，失效數據的可靠性高；當壽命x的取值接近xmax時，失效數據的可靠性低。在x=xmax之前，滾動軸承壽命試驗或服役過程中沒有出現失效，即僅獲得了無失效數據；在x=xmax時，失效數據的估計可靠性函數的可信度通常為85%～95%[7,13-14]，對應的c值約為0.1。

根據可靠性理論，預測滾動軸承壽命失效數據的可靠性函數r(u)為

根據(24)式及生成的多組大量無失效數據，可預測出滾動軸承壽命失效數據的多組可靠性函數。

1.5 預測真值函數及其上下界函數

設有S個失效數據，分別獲取同一失效數據所對應的多組可靠性函數的取值，將其構成一個滾動軸承壽命失效數據的可靠性數據序列R

R=(R1,R2,…,Rs);s=1,2,…,S，

(25)

Rs=(rs(1),rs(2),…,rs(j),…,rs(i));

j=1,2,…,i，

式中：s為失效數據可靠性數據序列的序號；Rs為第s個失效數據的可靠性數據序列；j為壽命失效數據的可靠性數據的序號；rs(j)為Rs中的第j個數據。

根據自助原理，從失效數據的可靠性數據序列Rs中等概率可放回地進行抽樣，抽取i次，可得到一個自助樣本Rsb，且其共有i個數據。連續重復抽取B次，得到B個自助再抽樣樣本，即失效數據的大量可靠性數據序列RB為

RB=(Rs1,Rs2,…,Rsb);b=1,2,…,B，

(26)

式中：Rsb為RB的第b個自助樣本。

運用最大熵原理，對于由 (26) 式模擬出的B個RB，用一連續變量z來表示失效數據的可靠性數據的自助樣本Rsb，根據 (4)～(20) 式，可得壽命失效數據可靠性的概率密度函數φ為

φ=φ(z) 。

(27)

預測滾動軸承壽命失效數據可靠性的真值函數RT為

(28)

假設顯著性水平α∈[0,1]，置信水平P為

P=1-α，

(29)

對應置信水平P=α/2處的置信區間的下邊界函數RL=Rα/2，且滿足

(30)

對應置信水平P=1-α/2處的置信區間的上邊界函數RU=R1-α/2，且滿足

(31)

因此，在置信水平P下，滾動軸承壽命失效數據可靠性的上界函數和下界函數可以用失效數據可靠性的取值區域D表示

D={RL,RU}={Rα/2,R1-α/2}。

(32)

2 研究案例

2.1 已知分布無失效數據

某滾動軸承的無失效數據見表1，共有6組11個數據。根據現有的可靠性研究[4]，認為滾動軸承壽命服從Weibull分布。

表1 滾動軸承的無失效數據

由表1可得滾動軸承的無失效數據序列X11(N=11)，如圖1所示。

圖1 滾動軸承的無失效數據序列X11

將這11個滾動軸承的無失效數據通過選擇抽樣個數進行分組:抽樣個數L1=5，L2=7，L3=8，L4=11，共4組自助抽樣。

設置信水平P=95%，根據自助最大熵法，分別對這4種情況的無失效數據建立失效數據的可靠性模型。

由自助最大熵法可得，理論上B的取值越大，預測的結果就越準確。在實際的案例分析中，當B取值過大時，會導致生成大量數據所用的時間過長；當B取值大到一定程度時，預測結果不再發生變化。因此，結合實際研究情況，在確保快速獲取最佳預測結果的前提下，優選B=30 000。

在建立失效數據的可靠性模型時，令B=30 000，c=0.1，進而可預測出4組滾動軸承壽命失效數據的可靠性函數，如圖2所示。

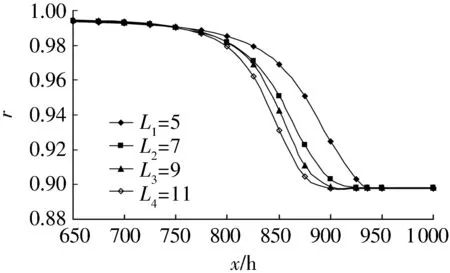
圖2 4組滾動軸承壽命失效數據的可靠性函數

由圖2可知，由于樣本的抽樣個數不同，獲得的每組有關滾動軸承失效數據的可靠性函數的具體變化有一定差別，但總體上來看，隨著滾動軸承試驗或服役時間的不斷增加，其壽命的可靠性均呈下降趨勢。該趨勢符合滾動軸承壽命在軸承試驗或服役過程中逐漸衰減的實際規律。

基于滾動軸承壽命同一失效數據對應的可靠性數據序列，運用自助最大熵法，令B=30 000，可得滾動軸承壽命失效數據的可靠性真值函數及其上下界函數，如圖3所示。圖中還給出了運用現有方法(多層Bayes估計法)對該滾動軸承無失效數據可靠性的分析結果[4]。

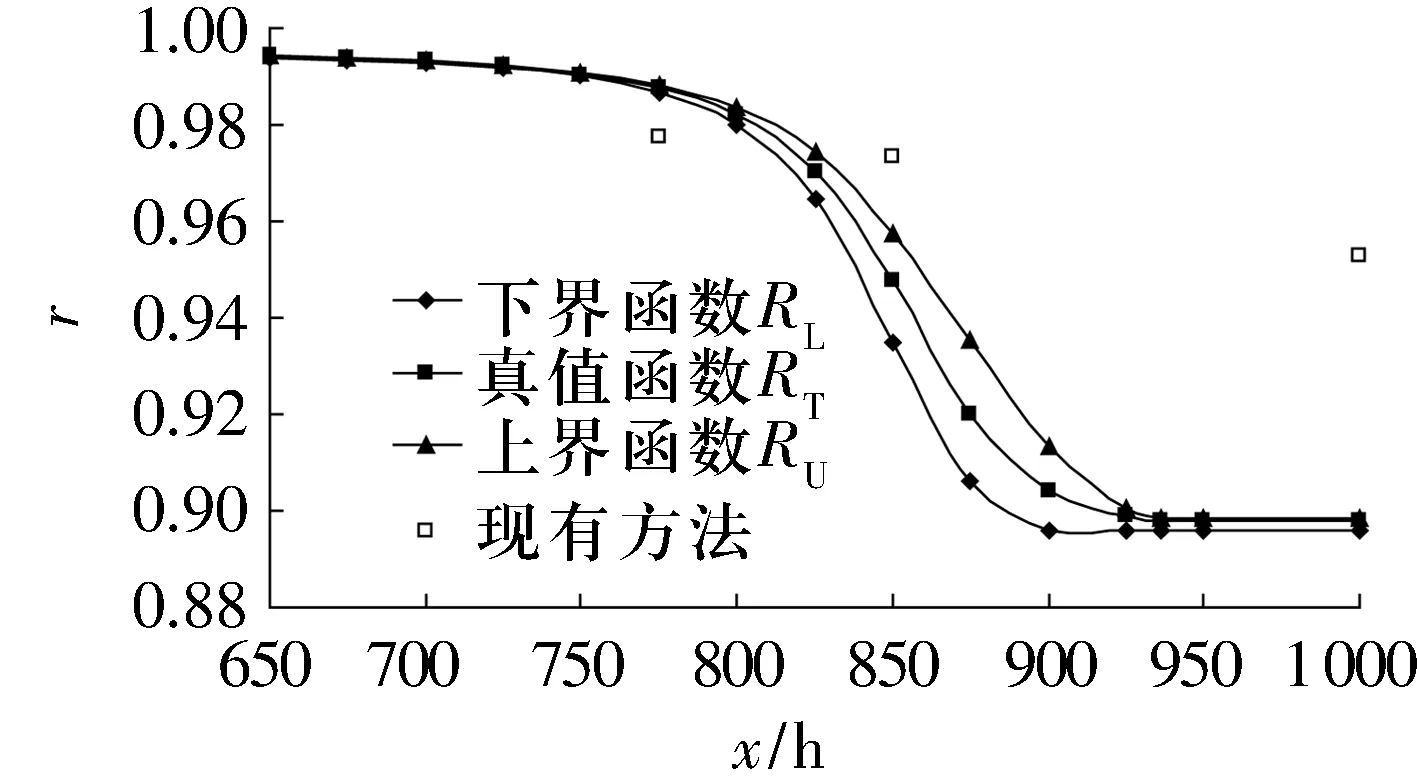
圖3 滾動軸承壽命失效數據可靠性的真值函數及其上下界函數

由圖3可知，當x=1 000 h時，由這2種方法得到的結果之間的差異最大。設x=1 000 h，用自助最大熵法預測的滾動軸承壽命失效數據可靠性估計真值RT(1 000)=89.82%。根據多層Bayes估計法，在滾動軸承壽命概率分布已知的條件下，假設滾動軸承壽命失效數據服從Weibull分布，當x=1 000 h時，計算的滾動軸承壽命失效數據可靠性為95.27%。二者最大差值為5.45%，相差很小，說明用自助最大熵法對滾動軸承壽命無失效數據的可靠性進行評估是可行的。

2.2 未知分布無失效數據

因滾動軸承壽命無失效數據來源于其運行時間，擬定一組數據作為壽命無失效數據，構成模擬無失效數據序列X10(N=10)，如圖4所示。由于模擬無失效數據是主觀擬定的，其概率分布是未知的。

圖4 模擬的無失效數據序列X10

將這10個模擬無失效數據通過選擇抽樣個數進行分組：抽樣個數L1=4，L2=6，L3=8，L4=10，共4組自助抽樣。

設置信水平P=95%，根據自助最大熵法，分別對這4種情況的無失效數據建立失效數據的可靠性模型。同理，令B=30 000，c=0.1，則可預測4組模擬失效數據的可靠性函數，如圖5所示。

圖5 4組模擬失效數據的可靠性函數

由圖5可知，由于樣本的抽樣個數不同，獲得的每組模擬的失效數據可靠性函數雖有一定差別，但總隨著模擬失效數據的不斷增大，滾動軸承壽命的可靠性整體呈下降趨勢。該趨勢符合滾動軸承壽命隨著時間推移逐漸衰減的實際規律。

基于同一模擬失效數據對應的可靠性數據序列，運用自助最大熵法，令B=30 000，可得模擬失效數據的可靠性真值函數及其上下界函數，如圖6所示。

由圖6可知，在模擬失效數據x取值范圍內，模擬失效數據可靠性的真值函數及其上下界函數均呈遞減趨勢，則預測的模擬失效數據可靠性的真值函數及其上下界函數符合滾動軸承可靠性逐漸衰減的實際情況，說明用自助最大熵法在概率分布未知條件下評估滾動軸承壽命無失效數據的可靠性是可行的。

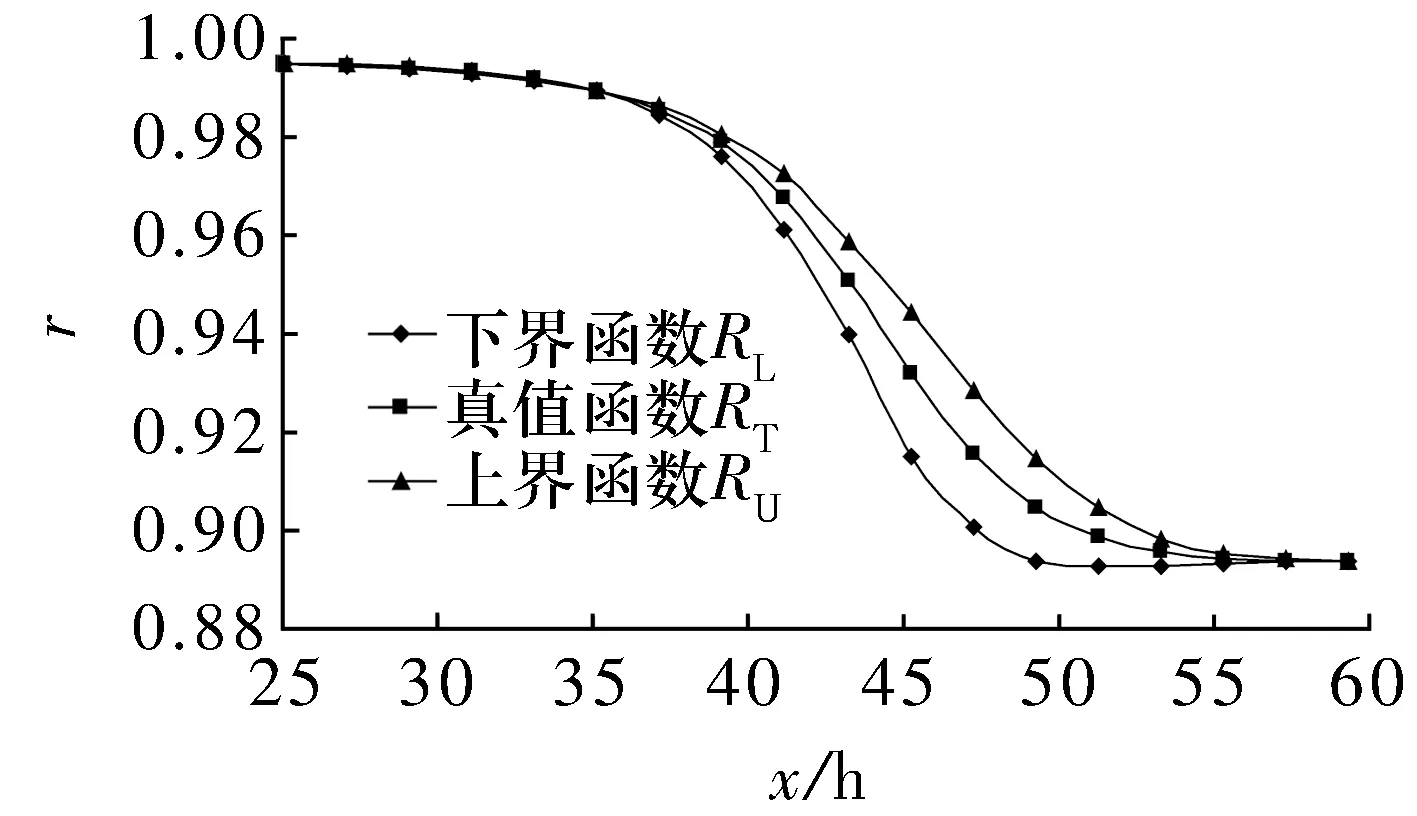
圖6 模擬失效數據可靠性的真值函數及其上下界函數

2.3 討論

已知分布無失效數據的實際案例為服從Weibull分布的壽命無失效數據可靠性評估案例,在概率分布已知的情況下，用自助最大熵法預測的壽命失效數據可靠性真值與現有方法得到的壽命失效數據可靠性取值相差很小，說明運用自助最大熵法可以較準確地預測壽命無失效數據的可靠性真值函數，該方法對于滾動軸承無失效數據的可靠性評估是可行的。另外，用自助最大熵法還可以預測出壽命無失效數據的可靠性上下界函數，而用現有方法是無法計算的。因此，在現有方法的可靠性研究中，可將自助最大熵法得到的壽命無失效數據可靠性上下界函數作為參考。

仿真試驗為概率分布未知的壽命無失效數據可靠性評估案例，由試驗結果可知，在概率分布未知的情況下，用自助最大熵法可以得到壽命失效數據可靠性的真值函數及其上下界函數。對比圖6和圖3可知，概率分布未知時預測的壽命失效數據可靠性真值函數及其上下界函數的變化規律與概率分布已知時預測的結果大致相同，說明自助最大熵法能夠解決在概率分布未知條件下對無失效數據的可靠性進行評估這一難題。而對于概率分布未知的情況，現有方法是行不通的。

3 結束語

在概率分布已知和未知的情況下，用自助最大熵法預測滾動軸承壽命的失效數據，經實際案例和仿真試驗證明，該方法對壽命的概率分布沒有要求，可以實現壽命無失效數據的可靠性評估。對于相同的一組無失效數據，運用現有方法和自助最大熵法獲得的可靠性結果是相同的，而實際工程上該結果有可能不同，在未來工作中有待深入研究。