角接觸球軸承的結構參數對接觸應力的影響及優化

張勝倫，徐華,，買買提明·艾尼，張磊

(1.西安交通大學 機械工程學院，西安 710049；2.新疆大學 機械工程學院，烏魯木齊 830047)

疲勞剝落是引起軸承失效的主要原因，而對于滾動軸承，疲勞主要指接觸疲勞。套圈和鋼球表面在接觸應力的反復作用下，其滾動表面金屬從基體呈點狀或片狀剝落下來[1]。作用于鋼球和溝道之間的載荷，僅能施加在二者之間很小的接觸區域。接觸表面上的高壓應力不會擴散到整個滾動零件中，接觸表面的破壞是研究的重點[2]，故有必要對滾動軸承的接觸應力進行分析。

角接觸球軸承的鋼球半徑和內、外圈的溝道曲率半徑直接決定了接觸橢圓區域的大小，其對接觸應力有直接的影響。文獻[3-6]對滾動軸承接觸應力已有大量的研究，而對于影響接觸應力的結構參數方面的研究涉及較少。文獻[7]對深溝球軸承的溝道曲率半徑對接觸應力和變形的影響進行了研究，但網格質量不高。文獻[8]研究了球徑、接觸角、溝道曲率等結構參數對接觸應力的影響。文獻[9]研究了不同外載荷和轉速下，軸承結構參數對其生熱和接觸應力的綜合影響。

現以B7008C角接觸球軸承為例，基于ANSYS Workbench運用局部網格細化方法，分析鋼球半徑和內、外圈溝曲率半徑系數等結構參數對接觸應力的影響。

1 理論計算

以B7008C角接觸球軸承為例分析，其結構參數見表1。

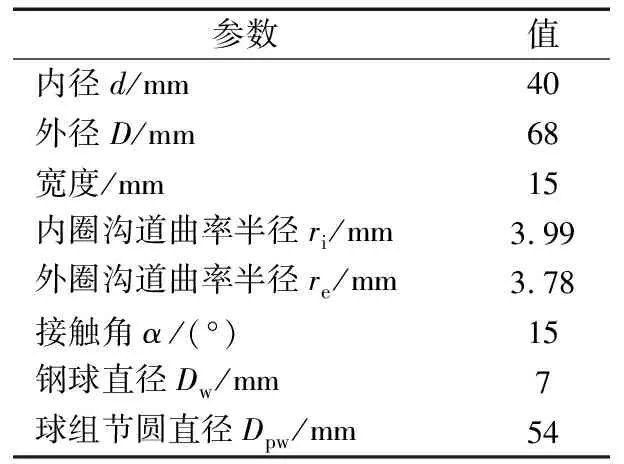
表1 軸承結構參數

軸承材料為GCr15軸承鋼，其材料參數為：密度ρ=7 830 kg/m3，泊松比ν=0.3，彈性模量E=207 GPa。

根據上述結構參數，不考慮游隙、潤滑、自旋和滑動等因素，建立的計算模型如圖1所示。

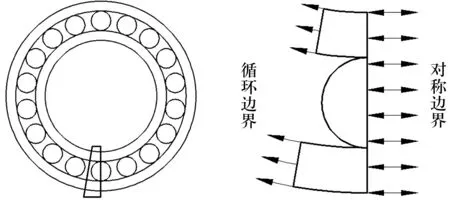
圖1 計算模型示意圖

根據圣維南原理[10]，選取一個鋼球單元的一半為計算對象，該鋼球與內外圈接觸區域的應力與其他鋼球接觸區域的應力之間的相互影響可以忽略。

根據Hertz接觸理論[11]可得接觸橢圓長、短半軸分別為

(1)

(2)

鋼球與內、外圈的最大接觸應力分別為

(3)

(4)

式中：a*，b*由主曲率差F(ρ)決定;∑ρ為曲率和系數；Q為鋼球載荷，為方便計算，取Q=100/cos 15°=103.528 N。

根據Hertz接觸理論可得ai=0.365 910 mm，bi=0.084 559 mm，ae=0.437 922 mm，be=0.085 900 mm，σimax=520.36 MPa，σemax=428.01 MPa。

2 有限元計算

2.1 建模與網格劃分

忽略圓角、游隙等，建立一個鋼球單元一半的三維模型如圖2所示。

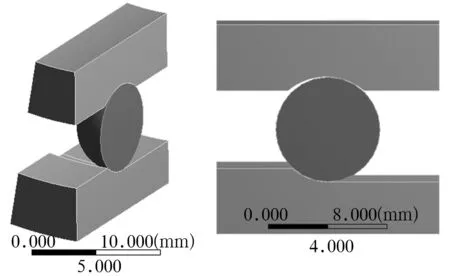
圖2 有限元計算模型

綜合運用虛擬球影響與膨脹層控制的先進網格劃分方法對上述模型進行接觸位置的局部細化。虛擬球半徑為0.6 mm，虛擬球內控制網格大小為0.02 mm，膨脹層總厚度為0.25 mm，總層數為7，層間增長率為1.2[12]。在接觸橢圓區域表面，單元體的邊長小于接觸橢圓短半軸長度的一半，在受力法向深度，單元體的邊長小于接觸橢圓短半軸長度的1/4[13]。網格劃分結果如圖3所示。

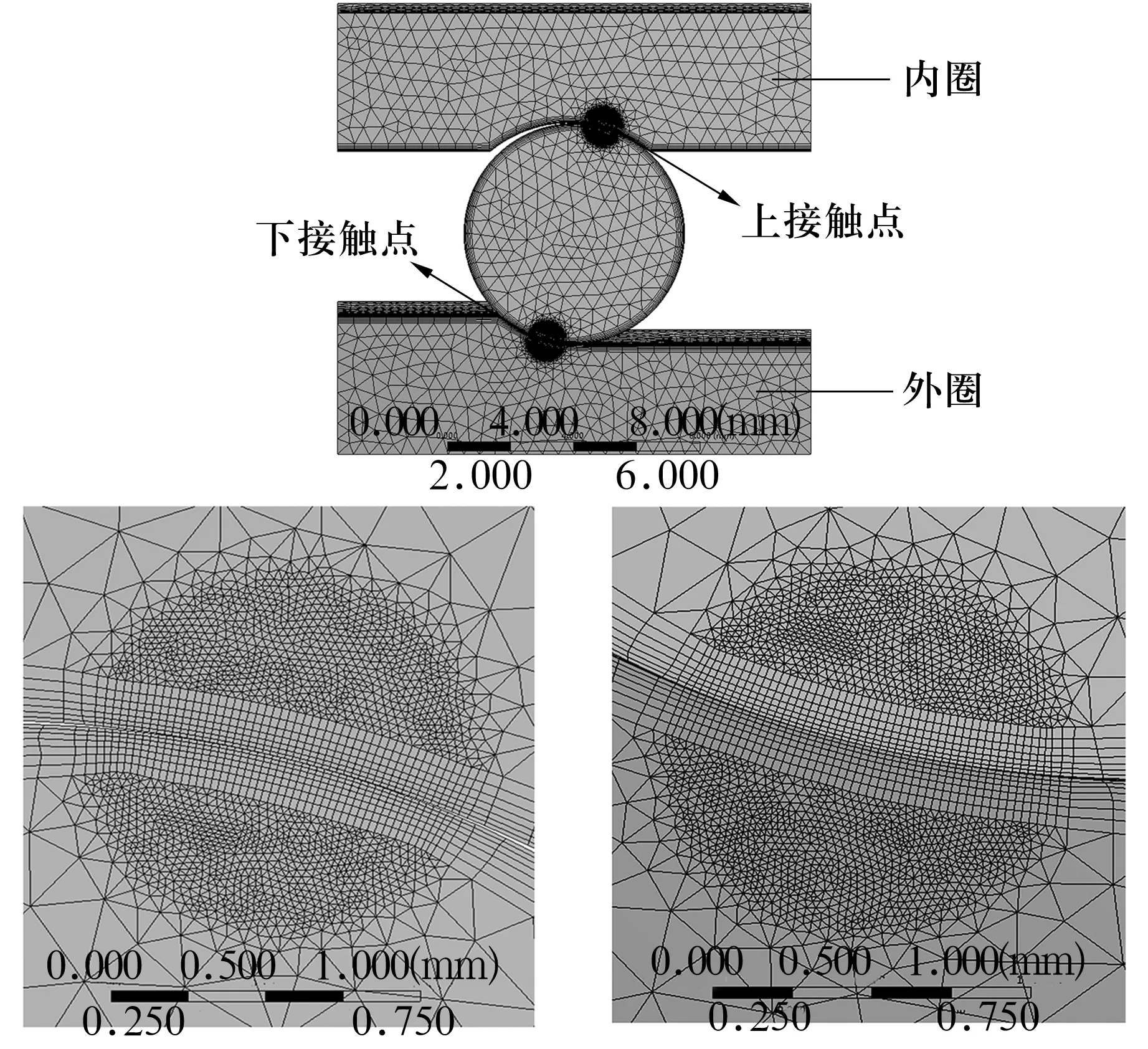
圖3 網格劃分

2.2 約束與載荷

在模型的內圈上施加100 N的純徑向載荷，設置軸承外圈固定。

2.3 接觸與邊界條件

鋼球與軸承內、外圈的接觸類型設置為摩擦接觸，摩擦因數為0.03。模型的截面和端面分別設置為圖1所示的對稱邊界和循環邊界。

2.4 結果與分析

經有限元仿真計算得該軸承的接觸應力云圖如圖4所示。由圖可知，鋼球與內外圈接觸的最大接觸應力分別為513.57， 423.74 MPa，與理論計算結果誤差不超過2%。由此可見，上述網格細化方法可精確計算接觸應力。與傳統理論計算相比，有限元分析計算簡單，更加形象直觀地建立軸承三維模型、設置合理邊界條件即可求解滾動軸承接觸應力。分析結構參數對接觸應力的影響時，只需修改三維模型和邊界條件即可，為軸承參數優化提供了更加便捷的途徑。

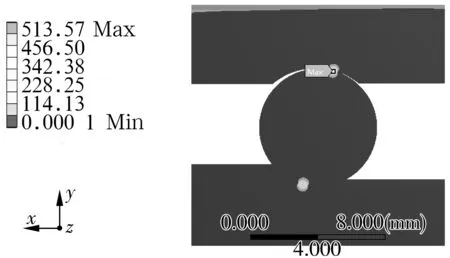
(a)整體模型視圖

3 結構參數對接觸應力的影響

3.1 鋼球半徑參數

軸承內、外圈溝道曲率半徑系數fi，fe不變，鋼球半徑分別為3.1，3.2，3.3，3.4，3.5，3.6，3.7 mm時，軸承最大接觸應力隨鋼球半徑參數的變化如圖5所示。

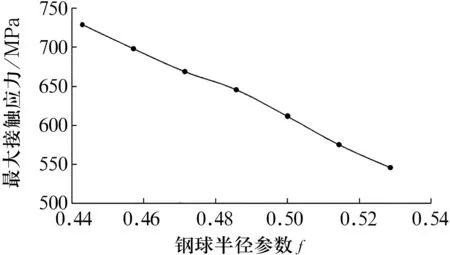
圖5 最大接觸應力隨f的變化

由圖5可知，最大接觸應力隨鋼球半徑參數f的增大而呈線性減小。這是由于隨f增大，接觸橢圓區域的面積增大，在載荷不變的情況下，模型的接觸應力逐漸減小；而鋼球與內圈的接觸區域面積總小于鋼球與外圈的接觸區域面積，故最大接觸應力一直位于鋼球與內圈接觸區域。

3.2 內溝道曲率半徑系數

f，fe不變，fi分別為0.514 3，0.528 6，0.542 9，0.557 1，0.571 4，0.585 7，0.6時，內、外圈最大接觸應力及整體軸承模型最大接觸應力隨內圈溝曲率半徑系數fi的變化分別如圖6、圖7所示。

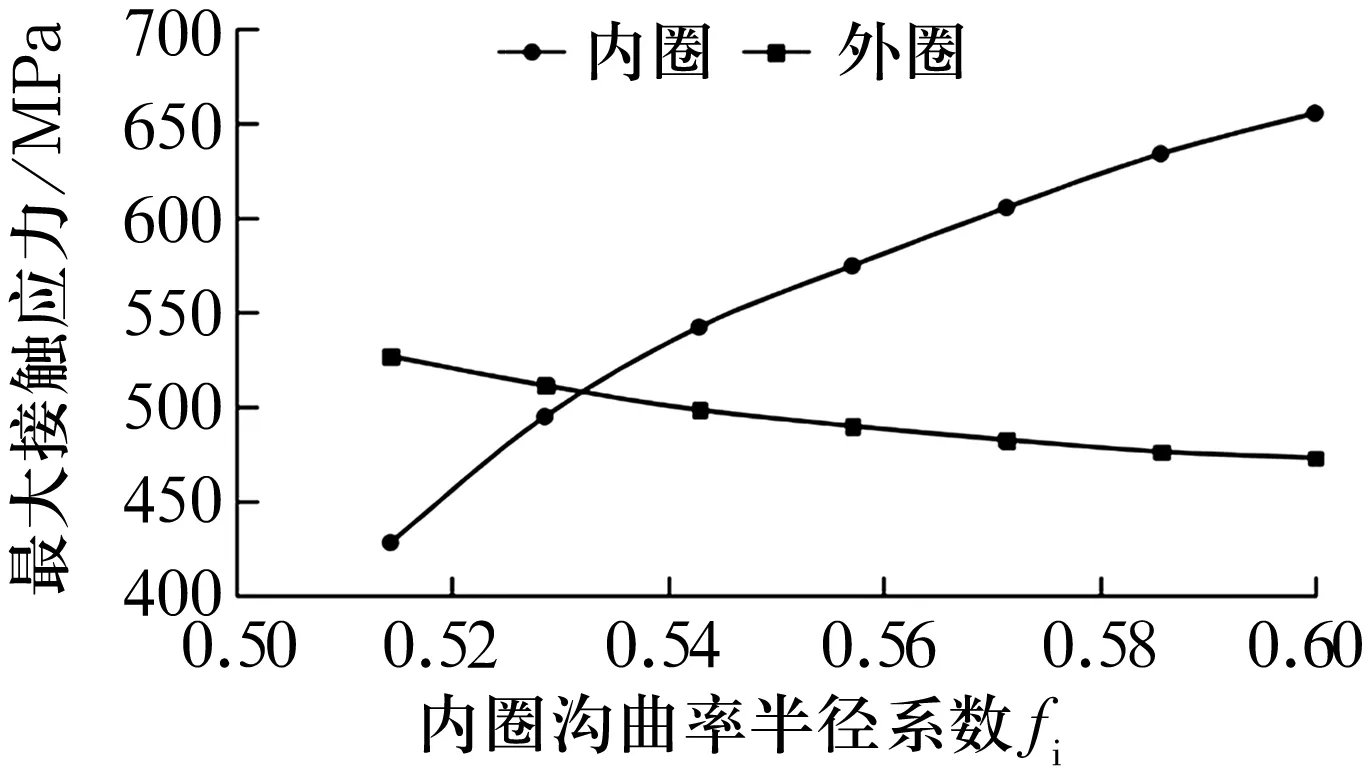
圖6 內、外圈最大接觸應力隨fi的變化

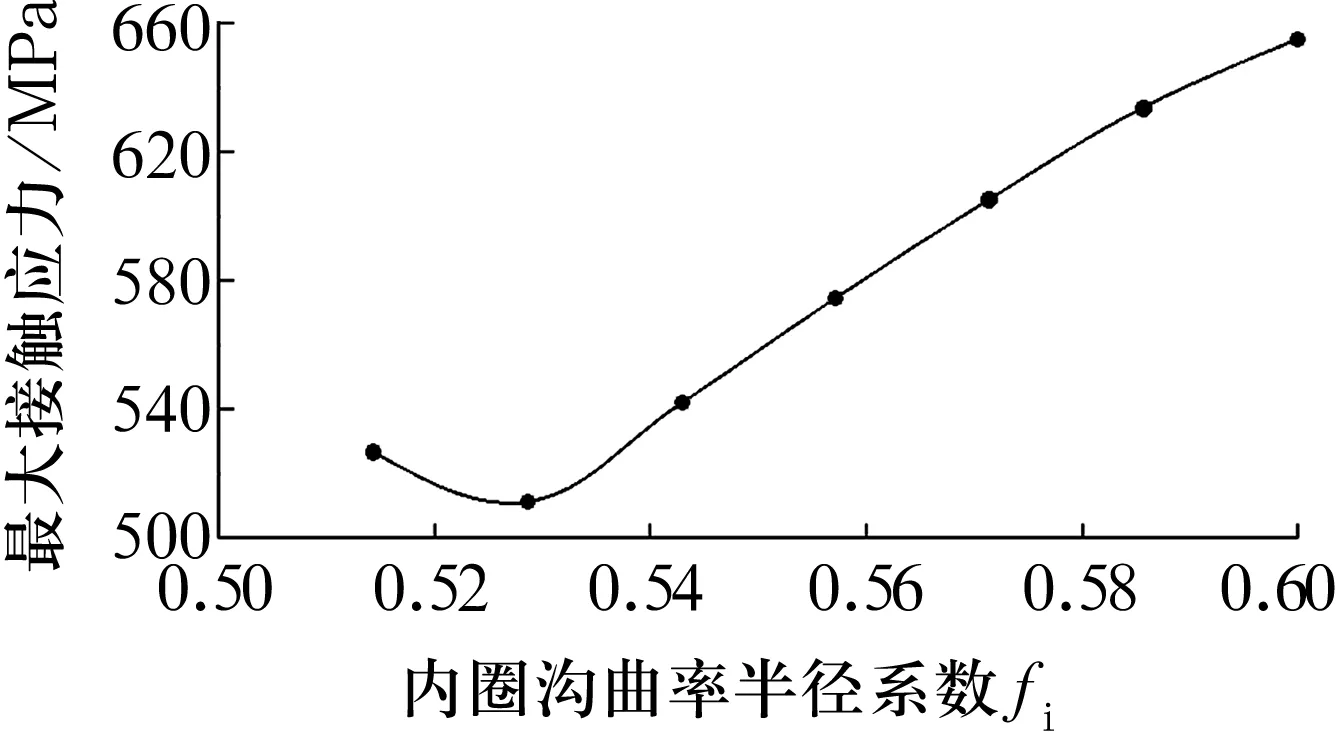
圖7 整體模型的最大接觸應力隨fi的變化

由圖6可知，隨fi增大，內圈最大接觸應力增大，外圈最大接觸應力逐漸減小，這是由于隨fi增大，鋼球與內圈的接觸區域面積減小，在載荷不變的情況下，內圈的接觸應力逐漸增大；由于應力分布不均勻，外圈的接觸應力有所減小。由圖7可知，整體軸承模型最大接觸應力先減小后增大。結合圖6和圖7可知，整體軸承模型最大接觸應力位置從鋼球與外圈接觸區域轉移到鋼球與內圈接觸區域。fi增大到0.542 9時，內、外圈最大接觸應力相等，此時整體軸承模型最大接觸應力值最小。故當f，fe不變時，fi存在最優解使整體軸承模型最大接觸應力值最小。

3. 3 外溝道曲率半徑系數

f，fi不變，fe分別為0.514 3，0.528 6，0.542 9，0.557 1，0.571 4，0.585 7，0.6時，內、外圈最大接觸應力及整體軸承模型最大接觸應力隨外圈溝曲率半徑系數fe的變化分別如圖8、圖9所示。

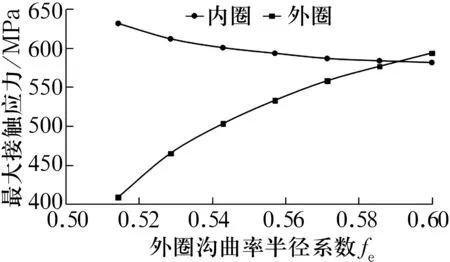
圖8 內、外圈最大接觸應力隨fe的變化

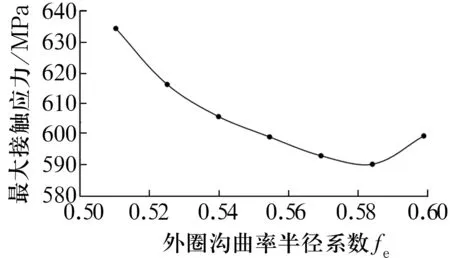
圖9 整體模型的最大接觸應力隨fe的變化

由圖8可知，隨fe增大，外圈最大接觸應力增大，內圈最大接觸應力逐漸減小。由圖9可知，整體軸承模型最大接觸應力先減小后增大。結合圖8和圖9可知，整體軸承模型最大接觸應力位置從鋼球與內圈接觸區域轉移到鋼球與外圈接觸區域。當fe為0.585 7時，整體軸承模型最大接觸應力最小。故同樣存在fe的最優解使得整體軸承模型最大接觸應力最小。

3.4 小結

根據等壽命原則[14],軸承設計時，應該使鋼球與內、外圈最大接觸應力相等。有限元計算表明，存在最優溝曲率半徑系數使得鋼球與內、外圈最大接觸應力相等，此時，整體軸承模型最大接觸應力值最小，而減小最大接觸應力可以顯著提高軸承疲勞壽命[2]。

4 結論

1)在ANSYS Workbench中合理運用局部網格細化方法，可以精確計算角接觸球軸承的接觸應力。

2)隨鋼球半徑參數增大，角接觸球軸承的最大接觸應力值呈線性減小。

3)存在最優內外圈溝曲率半徑系數使鋼球與內、外圈的接觸應力相等，且此時整體軸承模型最大接觸應力值最小。