基于變分模態分解參數估計的滾動軸承故障信息提取方法
楊洪柏,蔣超,石坤舉,劉樹林
(1.上海開放大學,上海 200433;2.上海大學,上海 200072)
變分模態分解(Variational Mode Decomposi-tion, VMD)假設信號由許多模態函數疊加而成[1],每個模態函數是具有不同中心頻率的調頻調幅信號,通過迭代搜尋構造變分模型的極值來確定每個模態函數(分量)的頻率中心及帶寬,從而實現信號的頻域剖分及各分量的有效分離。VMD具有堅實的理論基礎,其實質是多個Wiener濾波器組,表現出更好的模態分解效果及噪聲魯棒性[2-4]。但VMD的突出缺點是在信號分解之前必須事先給定模態數K,且分解的準確性依賴于K選擇的正確性,K的準確預估是VMD信號分解準確與否的關鍵[1]。
為解決以上問題,利用經驗模態分解(Empir-ical Mode Decomposition, EMD)無需預先設定模態數的自適應分解特點,通過EMD模態中真假模態的評估判斷評估出信號中所包含的有效模態數,并將其作為VMD處理過程中K的選擇依據,從而解決K給定的盲目性問題。
1 變分模態分解
VMD算法借用了EMD中本征模態函數(Intrinic Mode Function,IMF)的概念,但這一概念被重新定義為一個調幅調頻信號[1]
uk(t)=Ak(t)cosφk(t),
(1)
式中:φk(t)非遞減,φ′k(t)≥0;包絡線非負,Ak(t)≥0;并且包絡線Ak(t)與瞬時頻率ωk(t)=φ′k(t)相對于相位φk(t)來說是緩變的。即在[t-δ,t+δ](δ=2π/φ′k(t))的間隔范圍內,uk(t)可以看作是一個幅值為Ak(t)、頻率為ωk(t)的諧波信號。
為了構造變分模型,需經過如下步驟:1)通過Hilbert變換得到每個模態函數uk(t)的解析信號,從而獲得信號的單邊頻譜;2) 每個模態函數圍繞各自估算的中心頻率,通過指數修正調制到相應基頻帶;3) 通過高斯平滑解調信號獲得每段帶寬,即L2范數梯度的平方根。構造出受約束的變分模型為

(2)
為求取上述約束變分模型的最優解,即各個模態函數,引入懲罰因子α構造如下形式的增廣Lagrange函數,即
L({uk},{ωk},λ)=
,(3)
式中:α為懲罰參數;λ為 Lagrange乘子。
將上述Lagrange函數從時域變換到頻域,并進行相應的極值求解,分別得到模態分量uk和ωk的頻域表達式,即
(5)
然后利用交替方向乘子算法(Alternate Direction Method of Multipliers,ADMM)求約束變分模型的最優解,從而將原始信號分解為K個窄帶模態分量。具體算法如下:

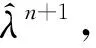
從算法中看出,K需要預先給定。為驗證K的選擇對分解模態的影響,構造了一個三分量的合成信號,即
f=cos(2π2t)+0.3cos(2π35t)+
0.02cos(2π300t)。
(6)
K取1~10分別進行研究,通過觀察信號的分解結果可知:K>3時會產生過分解,原始信號中的某個分量會被分解成多個模態,原始分量被分解得面目全非,且運算量大;K<3時會出現欠分解,其中的某個分量要么被拆分后疊加到相鄰的分量上產生混疊,要么信息被丟失;K=3時,預設值與實際模態數吻合,分解出比較精準的模態各分量。從仿真結果看,在K選取合理的情況下,能夠從原始信號中分解出精度較高的分量,不會產生混疊和過分解現象。因此,K的預先合理估計對于VMD的應用具有重要意義。
2 K的估算方法
EMD[5]的本質是將多分量非平穩信號分解成具有窄帶頻率成分的一系列近乎平穩的本征模態函數,其無需信號的先驗知識,分解過程完全由數據自身驅動,本征模態函數自適應地從原信號中分解得到,是后驗、完全自適應地分解[6-9]。因此,嘗試應用EMD自適應分解的特性,來評估有效的模態數,作為VMD算法中K的估計值,使VMD得到精度較高的模態分量。
2.1 無噪仿真信號的K估計
對于無噪信號的K估計,仍用(6)式的仿真信號進行研究。首先進行EMD處理,得到與原始分量一致的3個模態分量,即K=3;然后用K=3進行VMD處理,也準確分解出來3個模態分量。在這種情況下,VMD與EMD的精度區別不大,但是驗證了K的估值是有效的。
2.2 含噪仿真信號的K估計
對于含噪信號的K估計,在(6)式的基礎上加入強度為0.1的加性高斯白噪聲η,即
f=cos(2π2t)+0.3cos(2π35t)+
0.02cos(2π300t)+η。
(7)
應用EMD對信號進行分解,得到6層模態分量(圖1a),從圖中可以看出產生了一些虛假分量,無法直接獲取有效分量個數。因此,對各模態分量進行頻譜分析,結果如圖1b所示:模態1和模態2的頻譜頻帶很寬,可視為噪聲,無頻率中心;模態3和模態4的頻譜都在36 Hz左右,可認為這2個分量具有一個頻率中心;模態5和模態6可分別視作一個獨立分量;因而整個頻譜圖可分為3個模態分量,即K=3。
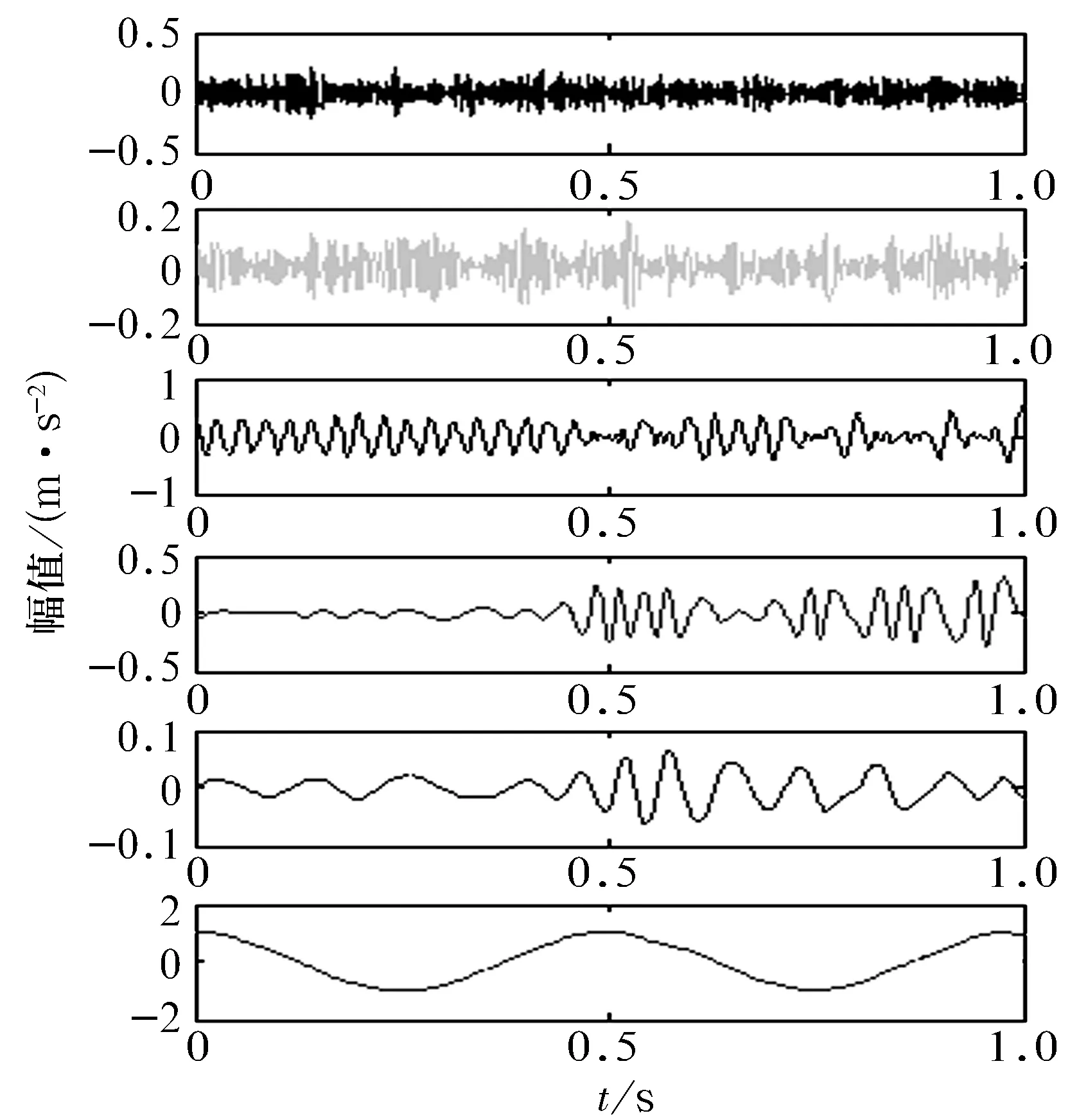
(a) 各模態分量
選擇K=3對信號進行VMD處理,得到3個模態分量及其頻譜圖,如圖2所示。
從圖2可以看出:原始信號角頻率分別為12.57,219.9和1 885 rad/s的3個模態分量被如實重現;低頻部分與原輸入信號吻合,還原精度高;高頻部分(300 Hz)由于受噪聲影響較大,幅值存在誤差,但仍能準確反映信號頻率。與圖1相比,VMD可以分解出頻率中心和頻帶確定的模態分量,且在噪聲方面具有較強的魯棒性。

(a) 各模態分量
3 實測故障信號分析
為驗證上述模態數估計方法在實測滾動軸承故障特征提取中的有效性,且能得到更為清晰的特征信號。現以Case Western Reserve University軸承數據中心的內圈故障數據為例進行分析。試驗軸承為6205-2RS JEM SKF深溝球軸承,采樣頻率為12 kHz, 轉速為1 730 r/min,軸承內圈故障特征頻率理論計算值為156.1 Hz。
對該內圈故障信號進行EMD處理,得到12層模態分量,為節省空間,選取前6層模態分量及其包絡譜進行顯示,如圖3所示。從圖中可以看出:前3層模態分量的包絡譜具有155.3 Hz(可視為實際的故障特征頻率)及其2倍頻的特征信息;第4層僅能夠得到155.3 Hz的故障信息,2倍頻信息已被淹沒;后8層模態分量基本無法提取出故障特征信息;因而可認為前4層為有效特征信息,即預估K=4。
選取K=4進行VMD處理,得到的模態分量及其包絡譜如圖4 所示。對比圖3可知:VMD的4個模態分量都具備155.3 Hz及其2倍頻的特征信息;且VMD各模態分量中特征頻率的幅值都要大于EMD各模態分量的對應幅值,特征信息周圍噪聲也相對少,特征信息部分更為凸顯。

(a)各模態分量
取K=5進行VMD處理的結果如圖5所示,其中模態5的特征信息非常微弱,其2倍頻的故障特征信息幅值僅有0.003,且淹沒于周邊噪聲之中,說明K=4的估值最為合適,模態數的估計方法有效可行。

圖5 VMD各模態分量包絡譜圖(K=5)
4 結束語
VMD在分解模態分量的準確性、精度和噪聲魯棒性方面具有一定的優勢,但受參數K的影響較大。從仿真信號和滾動軸承實測信號分解結果看,利用EMD自適應特性對K進行預估確實有效、可行。但當前方法仍基于人工分析,帶有一定的經驗性,下一步需進行K的自動獲取研究,提供更準確的估計,為后續的智能診斷提供依據。

