典型通信信號細微特征的小波分析與提取問題研究

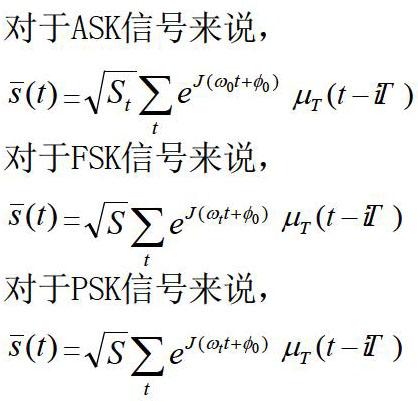
摘 要：小波分析與實際的工程有著緊密的聯系，其能夠對大部分函數空間進行簡單刻畫，能夠通過小波展開系數來對函數性質進行描述。對于通信信號的分析來說，小波分析有著局部分析性能優越的優勢，其在數據壓縮、邊緣檢測、降噪等方面的應用十分廣泛。基于以上，本文首先簡要分析了典型通信信號細微特征的小波分析，并探討了信號細微特征的提取問題，旨在為相關典型通信信號細微特征的提取和分析實踐提供參考。

關鍵詞：典型通信信號；細微特征；小波分析；提取

小波是一種先進的時頻分析理論，其在各個領域的分析中都有著廣泛的應用。對于通信領域來說，小波分析在典型通信信號細微特征方面有著較大的優勢，其在數據壓縮、邊緣檢測等方面的應用效果良好。基于以上，本文簡要研究了典型通信信號細微特征的小波分析和提取問題。

1 典型通信信號細微特征的小波分析

相較于傳統的傅里葉變換來說，小波變換在時域和頻域的局部化性質十分良好，小波變換提出了變化的時間窗，如果需要低頻信息，則采用長時間窗，能夠有效提升頻率分辨率，如果需要高頻信息，則采用短時間窗，能夠有效提升時間分辨率，從而保證了信息的精確性。小波變換采用的是時間-尺度域，采用的時間窗與尺度呈正比例關系，尺度越大，采用的時間窗越長，頻率越小，尺度越小，采用的時間窗越短，頻率越大。

對ASK、FSK、PSK等三種典型的通信信號進行小波變換：

在上述公式中，S代表信號的能量，3558077.png代表載波頻率，采樣過程中3558068.png遠遠小于π，3558060.png代表初相，3558052.png代表單位幅度的句型函數，[0，T]為其支撐區間，T代表信號的碼元周期[1]。不同典型通信信號在經過小波變換之后，其時頻圖有著一定的差異性，細微特征也有著一定的規律：

首先，對于單極性ASK這一典型通信信號來說，其載波頻率有著恒定性的特點，在載頻附近能量集中，不同碼元時刻的幅值有著一定的差異性，而對于小波系數圖來說，其變化也體現在能量變化上。需要注意的是，對于雙極性ASK信號來說，其不僅表現為能量變化，還表現為相位跳轉變化。

第二，對于FSK這一典型通信信號來說，其載波頻率不再是一成不變，不同碼元時刻的頻率有著一定的差異性，因此在經過小波變換之后，其小波系數圖為階梯狀，在不同的尺度集中能量[2]。如果載頻已知，則可以通過小波變化公式來推斷尺度范圍，如果尺度范圍已知，則可以對載頻的大小進行推算。

第三，對于PSK這一典型通信信號來說，其載波頻率有著恒定的特點，在馬原轉換時刻存在相位跳變的變化時，會產生頻率分量，其能夠反映在小波系數圖上。如果在碼元轉換時刻并沒有出現相位跳轉變化，則其特征表現為載頻性質特征，而出現相位跳轉的時候在小波系數圖像上會反映為突變，代表著相應頻率分量的產生。

2 典型通信信號細微特征提取分析

利用小波基能夠對典型通信信號中的“指定時間”變化和“制定頻率”變化等細微特征進行提取，“指定時間”變化的提取指的是小波在某時間發生的小波動，“指定頻率”變化的提取指的是低頻率成分以及高頻率成分的提取[3]。

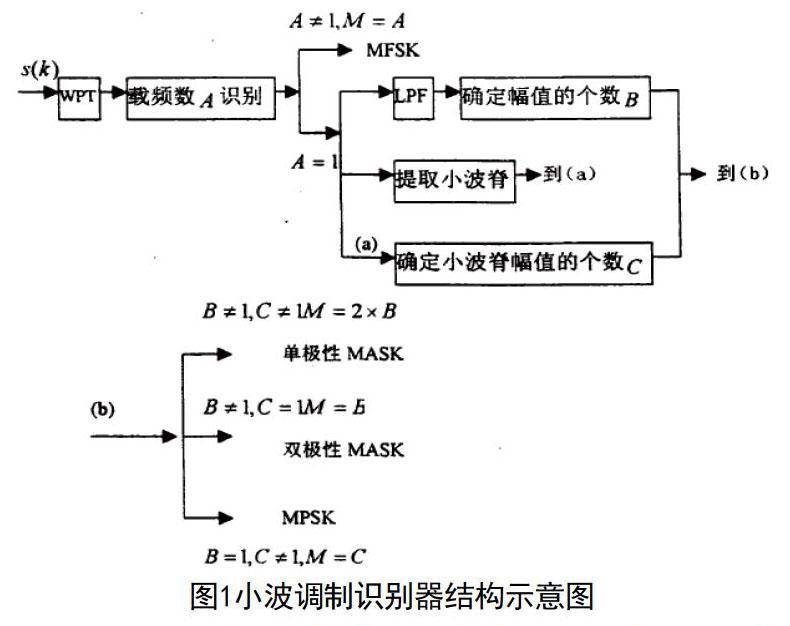
針對上文中典型通信信號小波分析特征，構造小波調制識別器，其結構圖如圖1所示：

對于小波變換來說，其平移參數和尺度都屬于連續變量，這就決定了小波變化的大冗余度，其計算相對復雜，在實際問題數值計算過程中，主要應用離散小波變換，對典型通信信號進行離散小波變換，得到的高低頻信號占據一半的頻帶，之后不斷進行離散小波分解，降低冗余度和計算復雜度，但需要注意的是，在此過程中也降低了時頻分辨能力，不利于典型通信信號的提取。因此本文提出的小波調制識別器中主要采用小波包變換，其與一半離散小波函數相似，小波包基包含的視頻窗能夠對整個時頻空間覆蓋[4]。但相較于一般的離散小波來說，小波包變換不僅能夠實現低頻部分的分解，同時能夠實現高頻部分的分解，在這樣的背景下，其時頻元形狀與位置之間沒有直接聯系，相較于離散小波來說，其分辨率更高。

對ASK、PSK、FSK三種典型的通信信號進行小波包變換，通過變換結果可知，在進行4級16層分解的過程中，4ASK信號結果能量在一層集中，在碼元時刻，隨著碼元的變化，能量值也出現變化，對于FSK信號來說，其能量在四個層次中分布，不同碼元能量隨著碼元變化而出現變化，對于PSK信號來說，其在一個層次集中能量，其能量是一個恒定的值。

在細微特征信號提取的過程中，主要設定三個步驟：①對門限進行設定，以此來對能量分布層次進行判斷，提取能量分布信息，從而將FSK這一典型通信信號區分出來，在層次個數為多個情況下，還能夠提取出FSK信號M數這一細微特征；②在經過小波包變換之后，如果能量在一層集中，提取此層信號中的低通濾波特征和小波脊特征[5]；③對提取的低通濾波和小波脊進行抽樣判決處理，對低通濾波處理后的幅值特征和小波脊的起伏變化進行判斷，如果低通濾波幅值有多個，而小波脊沒有出現起伏變化，則可以判斷信號為單極性ASK信號，且確定幅值個數M，如果低通濾波幅值有多個，但小波脊有起伏變化，則可以判定信號為PSK，如果低通濾波幅值沒有出現變化，小波脊出現起伏變化，則可以判定信號為PSK，確定小波脊包絡層次個數M。

3 結論

相較于其他時頻分析方法而言，小波變換分析有著時間局域化和頻域局域化的特點，小波在典型通信信號細微特征分析及提取的過程中有著重要的應用。本文以三種典型通信信號為例，對三種信號進行了小波變換分析，并探討了三種典型通信信號細微特征的提取，針對典型通信信號的特征提出了小波調制識別器和小波包變化提取方法。

參考文獻

[1]陸滿君，詹毅，司錫才，楊小牛. 基于瞬時頻率細微特征分析的FSK信號個體識別[J]. 系統工程與電子技術，2009，05：1043-1046.

[2]彭健航. 通信輻射源個體特征提取技術[J]. 電子測試，2012，07：6-14.

[3]周斌，王秀敏，果然，李紹濱，毛興鵬. 輻射源個體特征提取技術綜述[J]. 電訊技術，2011，06：162-168.

[4]孫娜. 通信電臺細微特征研究[D].北京郵電大學，2010.

[5]周斌. 信號細微特征提取及識別技術研究[D].哈爾濱工業大學，2011.

作者簡介

彭翔（1994-），男，安徽省無為縣，本科，通信工程。