《相似三角形的基本型》教學設計
賈國紅

一、教學內容分析
《相似三角形》是人教版義務教育課程標準實驗教科書《數學》(五四學制)第二十七章的內容,是全等變換之后的又一種圖形變換.全等是相似的一種特殊情況,從這個意義上講,相似比全等更具一般性.本節課主要復習了相似基本型,通過對相似基本型的歸納總結和習題的變換訓練,加深了學生對變換思想的認識,熟練了相似基本型的綜合運用.
二、教學對象分析
九年級學生已經學習了相似三角形的性質和判定,并進行了簡單的練習,但是在解決稍復雜的問題時,不會靈活運用相似基本型解決問題.針對此情況,我設計了這節復習課,加強學生對相似基本型的理解和應用.
三、教學目標及教學重難點
1. 教學目標
知識與技能:理解相似基本型的區別和聯系,能靈活運用相似基本型解決相關問題.
過程與方法:經歷觀察、思考、小組探究等活動,進一步體會轉化的思想.
情感、態度與價值觀:通過學生觀察、思考、小組探究等活動,提高學生合作交流能力、主動參與意識.通過小組合作交流活動,提高學生語言表達能力和邏輯思維能力.
2. 教學重點:相似三角形的基本型.
3. 教學難點: 相似基本型的綜合應用.
四、教學方法、過程及整合點
1. 教學方法
依據學生認知規律,遵循“學生為主體,教師為主導,數學活動為主線”的指導思想,采用以啟發引導為主,直觀演示法為輔的教學方法.適時運用多媒體教學,充分發揮現代教學手段的優越性.
2.學習方法
根據學法指導自主性和差異性原則,讓學生在“思考—操作—交流—歸納”的實踐探索中自主參與知識的產生、發展、形成與應用的過程,引導學生自己發現問題、提出問題、解決問題、拓展問題,指導學生用觀察、抽象、自主探究為主、合作交流為輔的方法進行學習.
3.教學過程及整合點
(1)“憶”——復習相似基本型主要有哪些
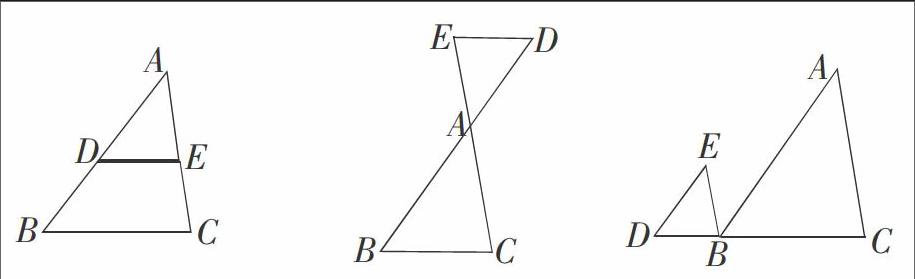
師生活動:總結相似基本型主要有三種:A型、X型、M型.
(設計意圖:回憶相似基本型的三種類型,加深對知識的整體認識.)
整合點與軟件:幾何畫板演示三種圖形,形象直觀.
(2)“清”——理清相似基本型的區別和聯系
師生活動1:觀察A型、X型、M型這三種相似基本型的區別,再思考它們之間有什么聯系.
師生活動2:小組交流三種相似基本型的區別和聯系.
師生活動3:歸納相似基本型的區別和聯系,突出本節課重點.
(設計意圖:經歷教師的演示、學生的探究過程,體會相似基本型之間的聯系和區別,為解決綜合題埋下伏筆.)
整合點與軟件:此環節是信息技術與課程整合點之一.幾何畫板的充分使用,解決了傳統教學中教師難以講述,學生難以理解的內容.
(3)“析”——分析如何選擇相似基本型解決問題
師生活動1:相似基本型的應用
如下圖,等邊△ABC中,D為BC中點,∠EDF=60°,當∠EDF旋轉一個角度時,觀察探索△BED和△CDF有什么關系.
師生活動2:找出△BED和△CDF相似,是M型相似.
師生活動3:如下圖,將等邊三角形變為等腰三角形,將中點D變為一般點D,結論還成立嗎?
師生活動4:總結解決問題的關鍵是找出相似基本型,為解決相似基本型的綜合應用這一難點打下基礎.
(設計意圖:此題是探索題,通過對等邊三角形中相似基本型M型的探索,發散學生的思維,鍛煉學生的毅力,同時也體現了團隊合作精神.總結圖形相似的有關特征并自覺應用到變式中,進一步豐富數學活動經驗,培養應用數學知識解決問題的能力.)
整合點與軟件:此環節是信息技術與課程整合點之二,這是一個動態圖形,從中找出靜態圖形, 利用幾何畫板將相似三角形拖拽出來,使學生看得更清晰.
(4)“練”——變式訓練,一題多解
師生活動1:提出動點問題.
已知菱形ABCD,AB=4cm,∠B=60°,點P、Q分別從點B、C同時出發,沿線段BC,CD以1cm/s的速度向終點C,D運動,運動時間為t秒.連AP,AQ,PQ,試判斷△APQ的形狀,并說明理由.
學生觀看演示,獨立思考,體會動點問題中哪些圖形全等,老師總結動中的不變.
師生活動2:如何解決動點問題和相似基本型的綜合題.
連接AC,與PQ相交于K,當t=1秒時,求AK的長.
學生探究后派代表演示找出的相似基本型.
師生活動3:由于學生表述得不夠完整,教師將找到的基本型進行演示,突破本節課難點.
(設計意圖:此題是探索結論題,體現了層次性,呈階梯逐步加深、加難,通過對結論的探索,復習相似三角形中的基本型.通過一題多變,培養學生的發散思維,拓展學生的解題思路.)
整合點與軟件:此環節是信息技術與課程整合點之三.幾何畫板的充分使用,變抽象為形象,變復雜為簡單,動中有靜,靜中有動,形象具體.幾何畫板呈現相似基本型,并從復雜的圖形中抽象出來,尋找題中的變量和不變量.
(5)“評”——對復習結果評價和反饋
師生活動:用“問卷星”的形式小結反饋.
(設計意圖:用此形式,可以靈活掌握學生對所學內容的掌握情況,以便對個性問題個別輔導,對共性問題集中講評.)
五、教學環境
根據教學內容、學生情況以及學校的實際情況,利用幾何畫板可以圖文并茂、聲像并舉、形象直觀地為學生創設各種情境,激起學生的各種感官參與,激發學生學習動機和興趣.數學科學的特點是邏輯性強、抽象思維要求高,尤其是空間問題、動態過程問題等學生不易理解的問題,通過這種方式可以使復雜的問題轉化為直觀、形象、生動的感性情景,大大降低了學生的理解難度和教師的教學難度.

