關(guān)于 I-正則空間和 I-正規(guī)空間的一個(gè)注記

李小敏

(石家莊理工職業(yè)學(xué)院,中國 石家莊　050228)

?

關(guān)于 I-正則空間和 I-正規(guī)空間的一個(gè)注記

李小敏

(石家莊理工職業(yè)學(xué)院,中國 石家莊050228)

摘要在拓?fù)淇臻g中引入理想結(jié)構(gòu)就形成了理想拓?fù)淇臻g, 理想拓?fù)淇臻g體現(xiàn)了拓?fù)浣Y(jié)構(gòu)和理想結(jié)構(gòu)的融合, 是一類重要的拓?fù)淇臻g, 研究它具有重要的理論價(jià)值. 給出了I-正則空間和 I-正規(guī)空間的映射定理及拓?fù)浜投ɡ? 得到了 I-正規(guī)空間的一些特征. 并討論了 I-正則空間、I-正規(guī)空間和 I-緊空間之間的關(guān)系.

關(guān)鍵詞理想空間; I-正則空間; I-正規(guī)空間; I-緊空間; 映射; 拓?fù)浜?/p>

Kuratowski[1]和Vaidyanathaswamy[2]在拓?fù)浣Y(jié)構(gòu)中引入了理想結(jié)構(gòu)，形成了理想拓?fù)淇臻g，它既有與一般拓?fù)淇臻g相似的性質(zhì)，又有獨(dú)特的性質(zhì). 于是研究理想拓?fù)淇臻g成為一般拓?fù)鋵W(xué)的重要課題之一. Arenas 等[3]研究了弱分離公理的理想化. Dontchev等[4]探討了理想可解拓?fù)淇臻g.Mukherjee等[5]運(yùn)用理想討論了拓?fù)淇臻g的擴(kuò)展.Navaneethakrishnan等[6]深入分析了理想拓?fù)淇臻g中g(shù)-閉集.Navaneethakrishnan等[7]研討了Ig-正則和Ig-正規(guī)空間.李招文等[8]考慮了理想Baire空間.陳海燕等[9]進(jìn)一步研究了理想拓?fù)淇臻g.但這些研究沒有涉及到了理想拓?fù)淇臻g的正則性和正規(guī)性.本文將研究I-正則空間和I-正規(guī)空間.

在本文中,空間總是指拓?fù)淇臻g或理想空間,它們不附加任何分離性,映射總是滿射.N表示自然數(shù)集,2X表示X的冪集.未涉及的拓?fù)鋵W(xué)方面的概念和符號(hào)均參見文獻(xiàn)[10].

設(shè)X是一個(gè)非空集，I?2X.I稱為X上的一個(gè)理想，如果它滿足如下條件:

(1) 若A∈I,B?A,則B∈I,

(2) 若A∈I,B∈I,則A∪B∈I.τ是X上的拓?fù)?I稱為X上的理想,則(X,τ,I)稱為理想拓?fù)淇臻g,簡稱理想空間.

設(shè)(X,τ,I)是一個(gè)理想空間.算子(·)*:2X→2X,稱為關(guān)于τ與I的局都映射[1],定義如下:對任意的A∈2X,A*(I,τ)={x∈X:V∩A?I,V∈τ(x)},其中τ(x)={V∈τ:x∈V}.

令cl(A)(I,τ)=A∪A*(I,τ).可證cl(·)*是一個(gè)Kuratowski閉包算子(參見文獻(xiàn)[11]).它生成一個(gè)比τ細(xì)的拓?fù)洇?(I,τ),我們稱為*-拓?fù)?在不引起混淆的前提下,

A*(I,τ)、cl*(A)(I,τ)和τ*(I,τ)分別簡記為A*、cl*(A)和τ*.

若X是一個(gè)拓?fù)淇臻g,且A∈2X,則cl(A)和int(A)分別表示A在X中的閉包和內(nèi)郎.若U?2X,Y∈2X,x∈X,則UY表示{A∩Y:A∈U},U(x)表示{A∈U:x∈A}.

若I是(X,τ)的理想，且Y∈2X,則IY是(Y,τY)的理想(參見文獻(xiàn)[12]).(Y,τY,IY)也是一個(gè)理想空間,我們稱(Y,τY,IY)為(X,τ,I)的子空間.

定義1設(shè)(Y,τ,I)是一個(gè)理想空間,且A∈2X.

(1) 若τ∩I=?,則I稱為codense理想[13].

(2) 若對點(diǎn)x∈X和滿足x∈F的閉子集F,存在X的互斥開子集U與V使得x∈U,F-V∈I,則X稱為I-正則的[14].

(3) 若對X的互斥閉子集A與B,存在X的互斥開子集U與V使得A-U∈I,B-V∈I,則X稱為I-正規(guī)的[15].

(4) 若對每個(gè)A的開復(fù)蓋U,U存在一個(gè)有限子集U′使得A-∪U′∈I,則A稱為X的I-緊子集[12].

(5) 若X作為一個(gè)子集是I-緊的,則X稱為I-緊空間.

顯然,若I={?},則正則性與I-正則性,正規(guī)性和I-正規(guī)性,緊性和I-緊性分別是一致的.

若映射f:X→Y是連續(xù)的閉映射,且對每個(gè)y∈Y,f-1(y)是X的緊子集,則f稱為一個(gè)完備映射.

引理1[13]設(shè)(X,τ,I)是一個(gè)理想空間,且A∈2X.若A?A*,則A*=cl(A*)=cl(A)=cl*(A).

引理2[11]設(shè)(X,τ,I)是一個(gè)理想空間,則I是codense當(dāng)且僅當(dāng)對每個(gè)G∈τ,有G?G*.

1關(guān)于I-正則空間的一些結(jié)果

引理3[16]若f:X→Y是一個(gè)映射,且A∈2X,B?Y,則f-1(B)?A當(dāng)且僅當(dāng)B?Y-f(X-A).

引理4[12]若(X,τ,I)是一個(gè)理想空間,(Y,σ)是一個(gè)空間,且f:(X,τ)→(Y,σ)是一個(gè)映射,則f(I)={f(I):I∈I}是Y上一個(gè)理想.

定理1設(shè)f:(X,τ,I)→(Y,σ,f(I))是一個(gè)完備映射.若X是I-正則的,則Y是f(I)-正則的.

證假設(shè)y?B,且B是Y的閉子集,則f-1(B)是X的閉子集.y?B推得f-1(y)∩f-1(B)=?.對每個(gè)x∈f-1(y),x?f-1(B).既然X是I-正則的,則存在互斥子集Ux,Vx∈τ使得x∈Ux和f-1(B)-Vx∈I.既然f是一個(gè)完備映射,則f-1(y)是X的緊子集.因?yàn)閧Ux:x∈f-1(y)}是f-1(y)的開復(fù)蓋,所以{Ux:x∈f-1(y)}有一個(gè)有限子復(fù)蓋{Uxi:i≤n}.令

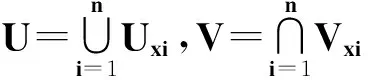
則U與V是X的互斥開子集.令G=Y-f(X-U),W=Y-f(X-V).既然f是一個(gè)完備映射,則G,W∈σ.現(xiàn)在f-1(y)?U,由引理3,y∈G.U∩V=?推得(X-U)∪(X-V)=X-U∩V=X.從而f(X-U)∪f(X-V)=Y.于是W∩G=?.

為了完成證明,需證明

B-W∈f(I).

令f-1(B)-Vx=Ax,則Ax∈I,f-1(B)?Vx∪Ax.

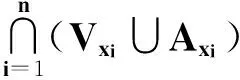
B-W?[Y-f(X-V∪A)]-[Y-f(X-V)]=f(X-V)-f(X-V∪A)?f((X-V)-(X-V∪A))=

f(V∪A-V)?f(A)∈f(I).

所以B-W∈f(I).

因此,Y是f(I)-正則的.

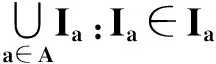
引理6若(X,τ,I)是I-正則的,且Y是X的閉子集,則(Y,τY,IY)是IY-正則的.

證假設(shè)y∈Y和F是Y的閉子集使得y?F,則存在X的閉子集A使得F=A∩Y.既然y?A,(X,τ,I)是I-正則的,于是存在互斥子集U,V∈τ使得y∈U,A-V∈I.

令I(lǐng)=A-V,則I∈I,A?A∪V=(A-V)∪V=I∪V.所以y∈U∩Y∈τY,V∩Y∈τY.

既然F-V∩Y?(I∪V)∩Y-V∩Y=(I∩Y)∪(V∩Y)-V∩Y?I∩Y∈IY.于是

F-V∩Y∈IY.注意到(U∩Y)∩(V∩Y)=?.因此(Y,τY,IY)是IY-正則的.

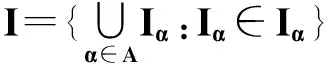
證必要性.對每個(gè)α∈Λ,IXα=Iα是顯然的.由引理6,Xα是Iα-正則的.

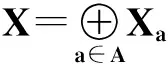
是Xα的閉子集.

顯然,存在β∈A使得x∈Xβ.既然x?F∩Xβ,Xβ是Iβ-正則的,則存在Xβ的互斥開子集U與V使得x∈U,F∩Xβ-V∈Iβ.既然Xβ是X的開閉子集,則U、V和X-Xβ都是X的開子集.顯然,Iβ?I.令F∩Xβ-V=A,則A∈I.

現(xiàn)在F∩Xβ?(F∩Xβ)∪V=(F∩Xβ-V)∪V?A∪V,

F=(F∩Xβ)∪[F∩(X-Xβ)]?A∪V∪(X-Xβ),

F-V∪(X-Xβ)?A∪V∪(X-Xβ)-V∪(X-Xβ)?A.

于是F-V∪(X-Xβ)∈I.注意到U與F-V∪(X-Xβ)是X的互斥開子集,則X是I-正則的.

2關(guān)于I-正規(guī)空間的一些結(jié)果

定理3設(shè)(X,τ,I)是理想空間,則下列條件等價(jià):

(1)X是I-正規(guī)的；

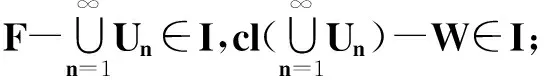
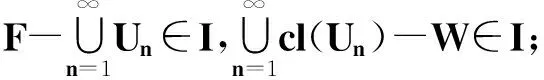
證(1)?(2)由文獻(xiàn)[15]中定理2.2推得.

(2)?(3)是顯然的.

(3)?(1).假設(shè)A與B是X的互斥閉子集.既然A∈X-B,存在X的開子集序列{Un}使得

既然B?X-A,存在X的開子集序列{Vn}使得

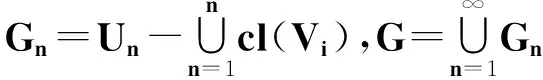
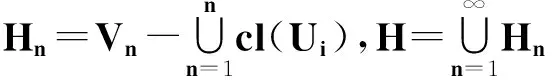
顯然,對每個(gè)n∈N,Gn和Hm都是X的開子集.于是G和H都是X的開子集.

斷言:對任意的n，m∈N,Gn∩Hm=?.

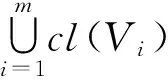
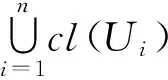
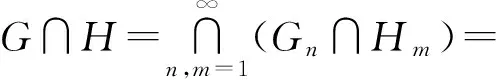
為完成證明,需證明A-G∈I,B-H∈I.

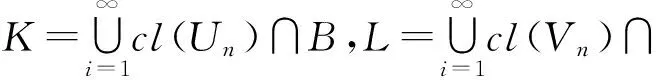
則P，Q,K,L∈I.我們將證明A?G∪P∪L,B?H∪Q∪K.對x∈A,(1)若x∈P∪L,則x∈G∪P∪L.

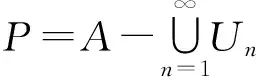
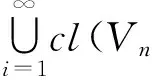
從而x∈Gm,所以x∈G∪P∪L.

因此,A?G∪P∪L.

類似地,可證B?H∪Q∪K.

既然

A-G?G∪P∪L-G?P∪L∈I,B-H?H∪Q∪K-H?Q∪K∈I，

那么A-G∈I,B-H∈I.

推論1(X,τ,I)是I-正規(guī)的,且Y是X的Fσ子集,則(Y,τY,IY)是IY-正規(guī)的.

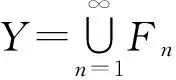
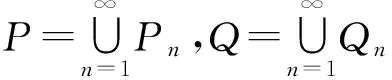
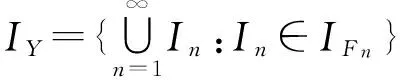
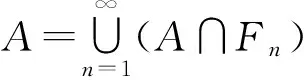
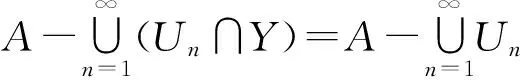
由Qn=cl(Un)-V,可推得cl(Un)?Qn∪V.

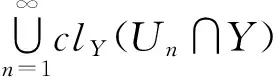
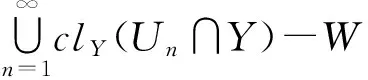
由定理3、引理1和引理2可得下列推論2.

推論2設(shè)(X,τ,I)是一個(gè)理想空間,則下列條件等價(jià):

(1)X是I-正規(guī)的;

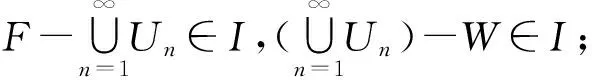
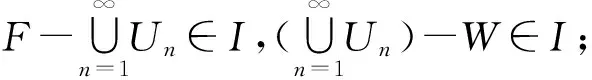
Renukadevi等[15]證明了I-正規(guī)空間在同胚映射f下的象是f(I)-正規(guī)空間.下列定理4改進(jìn)了這一結(jié)果.

定理4設(shè)f:(X,τ,I)→(Y,σ,f(I))是連續(xù)的閉映射.若X是I-正規(guī)的,則Y是f(I)-正規(guī)的.

證假設(shè)B1與B2是Y的互斥閉子集.既然f是一個(gè)連續(xù)映射,則f-1(B1),f-1(B2)是X互斥閉子集因?yàn)閄是I-正規(guī)的,則存在互斥子集U1,U2∈τ使得f-1(B1)-U1∈I,f-1(B2)-U2∈I.令A(yù)i=f-1(Bi)-Ui(i=1,2)則Ai∈I,f-1(Bi)?Ai∪Ui(i=1,2).

由引理3,Bi?Y-f(X-Ai∪Ui)(i=1,2).

既然

Bi-[Y-f(X-Ui)]?[Y-f(X-Ai∪Ui)]-[Y-f(X-Ui)]=

f(X-Ui)-f(X-Ai∪Ui)?f((X-Ui)-(X-Ai∪Ui))=f(Ai∪Ui-Ui)?f(Ai)∈f(I)(i=1,2),

則X.既然f是一個(gè)閉映射,則Y-f(X-U1)與Y-f(X-U2)是Y的互斥開子集.所以Y是f(I)-正規(guī)的.

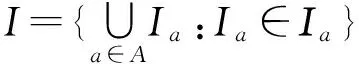
證必要性.由推論1可得.

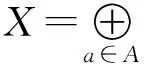
令

既然每個(gè)Xa是X的開子集,則U與V是X的開子集.

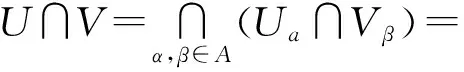
既然A∩Xa-U?A∩Xa-Uα，則A∩Xa-U∈Ia,于是

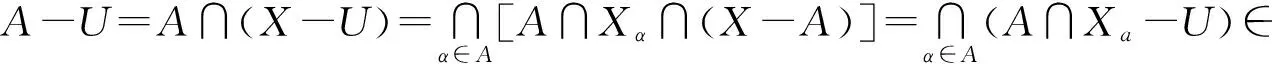
B-V∈I的證明是類似的.

因此X是I-正規(guī)的.

引理7設(shè)(X,τ,I)是一個(gè)理想空間.若X是一個(gè)Hausdorff空間,x?K且K是X的I-緊子集,則存在X的互斥開子集U與V使得x∈U,K-V∈I.

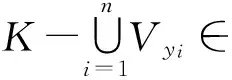
令

則U與V是X的互斥子集使得x∈U,K-V∈I.

定理6設(shè)(X,τ,I)是一個(gè)理想空間.若X是一個(gè)Hausdorff空間,A與B是X的互斥I-緊子集,則存在X的互斥開子集U與V使得A-U∈I,B-V∈I.

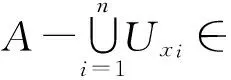
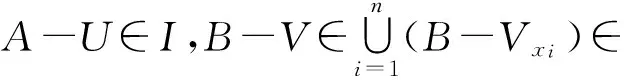
推論3若(X,τ,I)是I-緊、Hausdorff空間,則(X,τ,I)是I-正規(guī)的.

定理7若X是一個(gè)I-正則空間,則對任意X的I-緊子集A和A的開鄰或U,存在X的開子集V使得A-V∈I,cl(V)-U∈I.

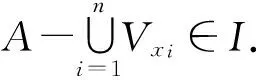
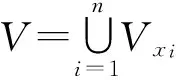
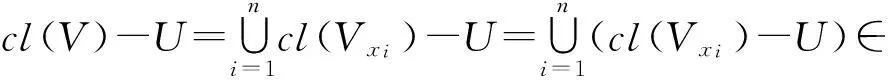
下列推論4改進(jìn)了文獻(xiàn)[15]中的推論2.10.

推論4若(X,τ,I)是I-緊、I-正則空間, 則(X,τ,I)是I-正規(guī)的.

參考文獻(xiàn)：

[1]KURATOWSKI K. Topology [M]. New York: Academic Press, 1966.

[2]VAIDYANATHASWAMY R. The localisation theory in set topology [J]. Proc Indian Acad Sci, 1945,20(1):51-61.

[3]ARENAS F G, DONTCHEV J, PUERTAS M L. Idealization of some weak separation axioms[J]. Acta Math Hungar, 2000,89 (1-2):47-53.

[4]DONTCHEV J, GANSTER M, ROSE D. Ideal resolvability [J]. Topol Appl, 1999,93(1):1-16.

[5]MUKHERJEE M N, BISHWAMBHAR R, SEN R. On extension of topological spaces in terms of ideals[J]. Topol Appl, 2007,154:3167-3172.

[6]NAVANEETHAKRISHNAN M, JOSEPH J P.g-Closed sets in ideal topological spaces [J]. Acta Math Hungar, 2008,119(2):365-371.

[7]NAVANEETHAKRISHNAN M, JOSEPH J P, SIVARAJ D.Ig-normal andIg-regular spaces [J]. Acta Math Hungar, 2009,125(2):327-340.

[8]LI Z, LIN F. On I-Baire spaces[J]. Filomat, 2013,27(2):303-312.

[9]陳海燕, 劉士琴, 王培, 等. 對理想拓?fù)淇臻g的進(jìn)一步研究[J]. 廣西大學(xué)學(xué)報(bào), 2008,33(1):79-82.

[10]ENGELKING R. General Topology [M]. Warszawa: PWN, 1977.

[11]JANKOVIC D, HAMLETT T R. New topologies from old via ideals [J]. Amer Math Monthly, 1990,97(2):295-310.

[12]NEWCOMB R L. Topologies which are compact modulo an ideal [D]. Califorlia: University of Califorlia at Santa Barbara, 1967.

[13]RENUKADEVI V, SIVARAJ D, CHELVAM T T. Codense and completely codense ideals[J]. Acta Math Hungar, 2005,108(2):197-205.

[14]HAMLETT T R, JANKOVIC D. On weaker forms of paracompactness, countable compactness and Lindelofness [J]. Ann New York Acad Sci, 1994,728(1):41-49.

[15]RENUKADEVI V, SIVARAJ D. A generalization of normal spaces[J]. Archivum Math, 2008,44(2):265-270.

[16]林壽. 度量空間和函數(shù)空間的拓?fù)鋄M]. 北京: 科學(xué)出版社, 2004.

[17]DONTCHEV J. On Hausdorff spaces via topological ideals and I-irresolute functions [J]. Ann New York Acad Sci, 1995,767(1):28-38.

(編輯CXM)

DOI:10.7612/j.issn.1000-2537.2016.04.011

收稿日期：2015-08-26

基金項(xiàng)目：國家自然科學(xué)基金項(xiàng)目(11461005)

*通訊作者,E-mail：lixiaomin8846@126.com

中圖分類號(hào)O189.1

文獻(xiàn)標(biāo)識(shí)碼A

文章編號(hào)1000-2537(2016)04-0066-06

A Note onI-Regular Spaces andI-Normal Spaces

LIXiao-min*

(Shijiazhuang Institute of Technology, Shijiazhuang 050228, China)

AbstractIntroducing ideal structures in topological spaces forms an ideal topological space. An ideal topological space reflects the integration of topological structures and ideal structures, and then is a kind of important topological space. Researching on it has important theoretical value. Map theorem and topological sum theorem on I-regular (resp. I-normal) spaces are given respectively. Some characterizations of I-normal spaces are obtained. Moreover, the relationship among I-regular, I-normal and I-compact spaces are discussed.

Key wordsideal spaces; I-regular spaces; I-normal spaces; I-compact spaces; maps; topological sums