非連續(xù)免疫策略對(duì)一類(lèi)計(jì)算機(jī)病毒模型的影響

李　迅, 張道祥, 昂蓉蓉

(安徽師范大學(xué)數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽 蕪湖 241002)

?

非連續(xù)免疫策略對(duì)一類(lèi)計(jì)算機(jī)病毒模型的影響

李迅, 張道祥, 昂蓉蓉

(安徽師范大學(xué)數(shù)學(xué)計(jì)算機(jī)科學(xué)學(xué)院,安徽 蕪湖 241002)

摘要：研究一類(lèi)右端不連續(xù)的計(jì)算機(jī)病毒傳播模型. 通過(guò)計(jì)算得到模型的基本再生數(shù)R0. 運(yùn)用微分包含的相關(guān)知識(shí), 給出該模型的Filippov解的定義, 證明了該非連續(xù)模型的平衡點(diǎn)的存在唯一性. 通過(guò)構(gòu)造合適的Lyapunov函數(shù), 證明了當(dāng)R0>1時(shí), 滿(mǎn)足初始條件的每一個(gè)解都是在有限時(shí)間內(nèi)全局收斂于地方病平衡點(diǎn); 當(dāng)R0<1 時(shí), 滿(mǎn)足初始條件的每一個(gè)解都是在有限時(shí)間內(nèi)全局收斂于無(wú)病平衡點(diǎn). 利用MATLAB軟件進(jìn)行數(shù)值模擬, 驗(yàn)證了理論結(jié)果的正確性.

關(guān)鍵詞：計(jì)算機(jī)病毒；非連續(xù)免疫策略；Lyapunov函數(shù)；有限時(shí)間全局收斂

0引言

伴隨著互聯(lián)網(wǎng)商業(yè)、工業(yè)和社會(huì)活動(dòng)的日益普及, 計(jì)算機(jī)病毒已經(jīng)嚴(yán)重威脅到信息安全, 導(dǎo)致組織蒙受巨大損失. 殺毒軟件在計(jì)算機(jī)病毒預(yù)防中發(fā)揮了重要作用, 但是它們總是滯后于病毒. 為了有效防范計(jì)算機(jī)病毒在網(wǎng)絡(luò)中的傳播, 需要了解各種病毒的傳播方式、修補(bǔ)的影響以及網(wǎng)絡(luò)拓?fù)涞惹闆r[1]．我們發(fā)現(xiàn)電腦病毒的傳播和人類(lèi)流行的蔓延之間具有很大的相似性[2]， 因此Kephart在此基礎(chǔ)上使用數(shù)學(xué)方法分析電腦病毒的流行[3]. 在這之后, 一些描述計(jì)算機(jī)病毒傳播特征的動(dòng)態(tài)模型被大量提出來(lái), 主要是SIR模型[4]和SIS 模型[5]，但是，這些模型沒(méi)有考慮預(yù)先免疫措施，于是文獻(xiàn)[6]根據(jù)實(shí)際情況, 提出了一個(gè)新的計(jì)算機(jī)病毒傳播SIRS模型, 充分考慮了預(yù)先免疫措施, 并對(duì)所提出模型的動(dòng)力學(xué)行為進(jìn)行了理論分析和實(shí)驗(yàn)驗(yàn)證. 但這些計(jì)算機(jī)病毒模型大都只考慮了連續(xù)的免疫過(guò)程.然而，不止在網(wǎng)絡(luò)世界中存在非連續(xù)的情況, 現(xiàn)實(shí)生態(tài)系統(tǒng)中也具有不連續(xù)現(xiàn)象[7-8], 本文由此對(duì)這種現(xiàn)象加以研究.

網(wǎng)絡(luò)中的節(jié)點(diǎn)可以看做是私人計(jì)算機(jī)或者服務(wù)器端等, 其中S表示處于易感染狀態(tài)的節(jié)點(diǎn), I表示處于已感染狀態(tài)的節(jié)點(diǎn), R 表示處于恢復(fù)狀態(tài)的節(jié)點(diǎn),文獻(xiàn)[6]主要提出了如下的模型:

(1)

其中：p為新節(jié)點(diǎn)的感染率；b為新節(jié)點(diǎn)的接入數(shù)；μ為節(jié)點(diǎn)死亡率；β為有效傳染率；k為反病毒措施的實(shí)施率；γ為已感染節(jié)點(diǎn)的治愈率.

由于存在非連續(xù)情況,本文考慮在上述模型中加入非連續(xù)免疫項(xiàng)h(I)：

(2)

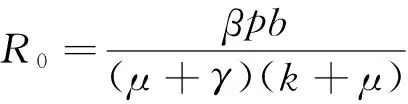
(A1). h(I)=φ(I)I,φ:R+→R+是一個(gè)非減的函數(shù), 并且在每一個(gè)緊致的區(qū)間內(nèi)至多有有限個(gè)跳躍間斷點(diǎn).

由于模型(2)的前兩個(gè)方程相對(duì)于變量R是獨(dú)立的, 所以只需要考慮下面的子系統(tǒng)：

(3)

由于在模型(3)的右邊部分存在一個(gè)非連續(xù)項(xiàng), 所以經(jīng)典的微分方程理論不能運(yùn)用在這里. 為了繼續(xù)接下來(lái)的研究, 則需要定義模型(3)其他形式的解, 這里引入了Filippov解的形式[9],考慮如下右端不連續(xù)微分方程：x′(t)=f(t,x(t))，其中f關(guān)于變量t是可測(cè)的且是局部有界的.

定義1考慮如下的集值映射：

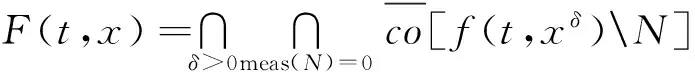
對(duì)于帶有初值的不連續(xù)微分方程,Filippov解是絕對(duì)連續(xù)的向量值函數(shù). 一個(gè)向量函數(shù)(S(t),I(t)),t∈(0,T),T∈(0,+∞)是模型(2)的一個(gè)解, 其中模型(2)的初始條件是S0=S(0)≥0,I0=I(0)≥0, 如果(S(t),I(t))在任意一個(gè)子區(qū)間[t1,t2]上是一致連續(xù)的, 則對(duì)于滿(mǎn)足初始條件的向量函數(shù)滿(mǎn)足如下的微分包含：

(4)

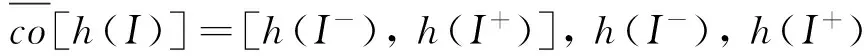
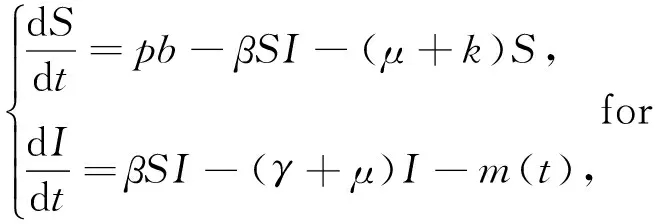
(5)

1平衡點(diǎn)及其存在唯一性

出于現(xiàn)實(shí)網(wǎng)絡(luò)世界中的考慮, 需要證明模型(3)滿(mǎn)足初始條件的解是有界且是正的.

命題1假設(shè)(A1)是成立的, 令(S(t),I(t))是模型(2)滿(mǎn)足初始條件S0=S(0)≥0,I0=I(0)≥0,t∈[0,T)的解, 則S(t)≥0, I(t)≥0，其中 t∈[0,T).

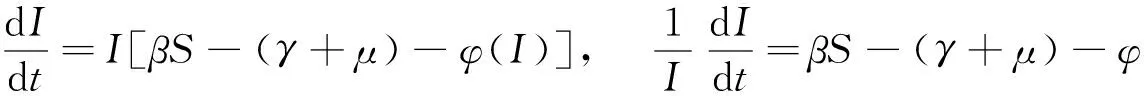
命題2假設(shè)(A1)是成立的, 且S(0)≥0, I(0)≥0, 模型(2)在(0,t0)上至少存在一個(gè)解(S(t),I(t))滿(mǎn)足S0=S(0), I0=I(0), 并且所有的解都是存在且有界的, 其中t∈[0,+∞).

由式(4)可以得到

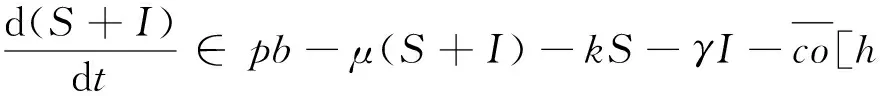
對(duì)于模型(3), 定義一個(gè)常數(shù)解(S(t),I(t))=(S*,I*), 如果(S*,I*)是模型的一個(gè)平衡點(diǎn)當(dāng)且僅當(dāng)

(6)

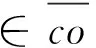
(7)

很明顯, 這里的ξ*是唯一的, 并且

若(A1)成立, 為了得到模型(3)的平衡點(diǎn), 需要解決下面的微分包含

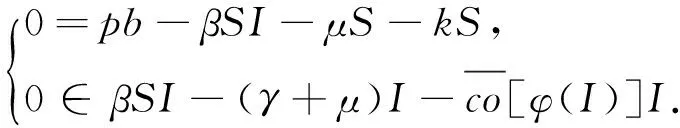
(8)

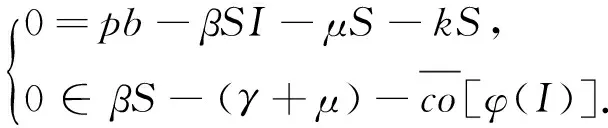
(9)

連立式(9)的兩個(gè)微分方程, 可以得到

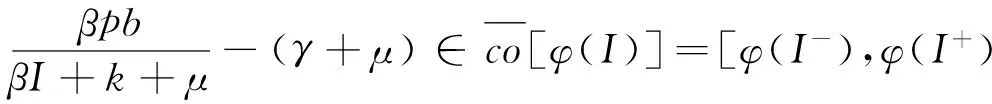
(10)

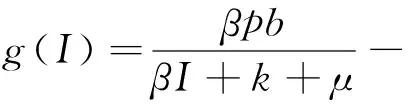
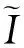
證明首先來(lái)證微分包含式(10)存在一個(gè)的正解, 由于R0>1, 則g(0)>φ(0)>0, 又g(I)是單調(diào)遞減函數(shù), φ(I)關(guān)于I是非單減的函數(shù). 另外, g(I)≤0 當(dāng)且僅當(dāng)

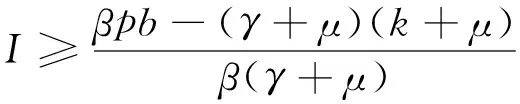
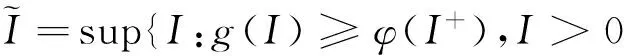
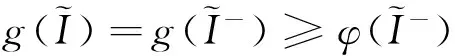
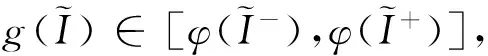
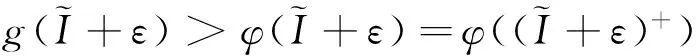
(11)

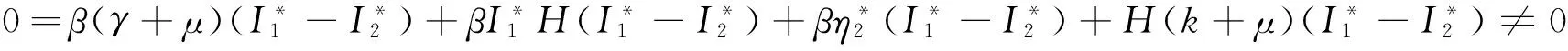
2有限時(shí)間內(nèi)全局收斂

這一部分主要通過(guò)構(gòu)造Lyapunov函數(shù), 證明無(wú)病平衡點(diǎn)和地方病平衡點(diǎn)是在有限時(shí)間內(nèi)到達(dá)平衡點(diǎn)的, 在開(kāi)始證明之前先介紹下面的一個(gè)假設(shè).

(A2). 假設(shè)R0>1且φ(I)在I*處有一個(gè)跳躍間斷點(diǎn), 其中I*是由引理1確定的唯一正解, 另外取

η*=βS*-(γ+μ)∈(φ((I*)-),φ((I*)+))，

根據(jù)(A2)可定義θ:=min{φ((y*)+)-η*,η*-φ((y*)-)}>0.

定理1在假設(shè)(A1),(A2)都成立的前提下, 模型(3)所有滿(mǎn)足初始條件的解都在有限時(shí)間內(nèi)全局收斂于平衡點(diǎn)E*=(S*,I*). 即當(dāng)所有的

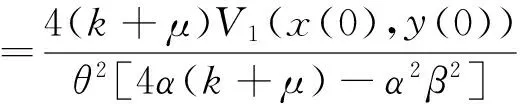
都有(S,I)=(S*,I*),t∈(0,+∞)，其中

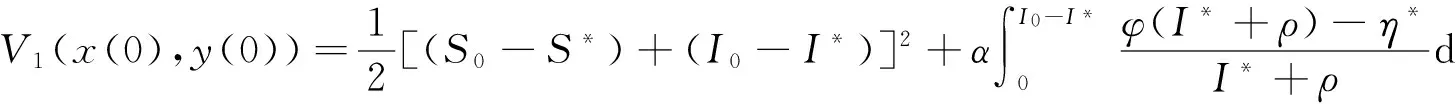
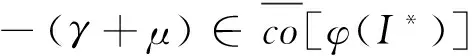
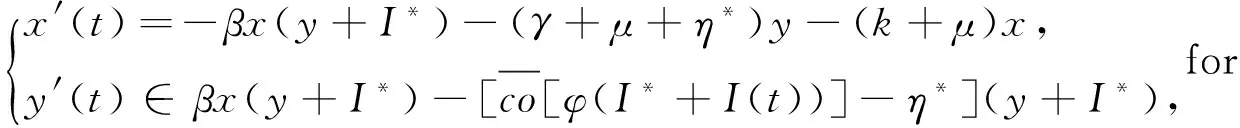
(12)

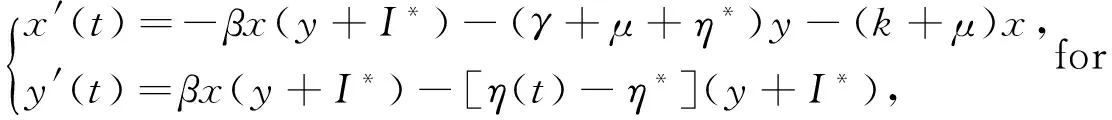
(13)

構(gòu)造如下的Lyapunov函數(shù)：

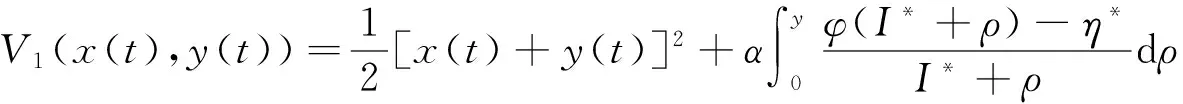
其中α是一個(gè)正常數(shù), 定理之后將給出它的取值范圍. 很明顯V1(x(t),y(t)) 是一個(gè)正則函數(shù), 當(dāng)(x(t),y(t))≠0時(shí), V1(x(t),y(t))>0且V1(0,0)=0; 當(dāng)x→+∞或y→+∞時(shí), V1(x(t),y(t))→+∞, 則有

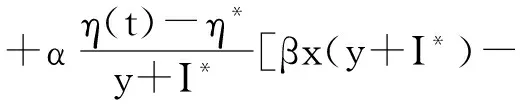
[η(t)-η*](y+I*)] ≤-(k+μ)x2+αβx[η(t)-η*]-α[η(t)-η*]2≤

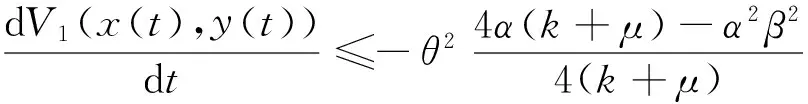
將上式兩邊從0到t積分可得

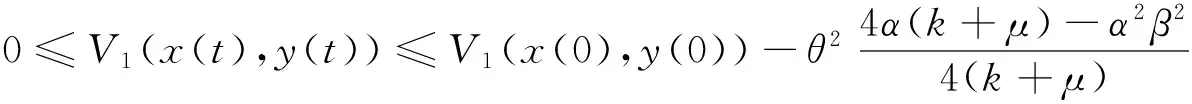
也就是說(shuō)當(dāng)t=t*時(shí),V1(x(t),y(t))=0, 其中

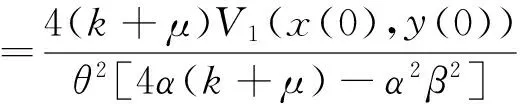
由文[11]知當(dāng)t>t*時(shí),可得(x(t),y(t))=0, 即當(dāng)t>t*時(shí),(S(t),I(t))=(S*,I*), 故定理1得證.

接下來(lái)我們希望得到模型的解可以在有限時(shí)間內(nèi)收斂于無(wú)病平衡點(diǎn)E0, 由于A1假設(shè)h(I)在I=0處是連續(xù)的, 所以在A1的前提下不能得到在有限時(shí)間內(nèi)收斂于無(wú)病平衡點(diǎn)E0, 因此需要給出以下假設(shè)：

(A3)h:R+→R+是一個(gè)非減且在每一個(gè)緊致區(qū)間內(nèi)至多有有限個(gè)跳躍間斷點(diǎn)的函數(shù), 此外h(0)=0，但是h(I) 在I=0處是不連續(xù)的.

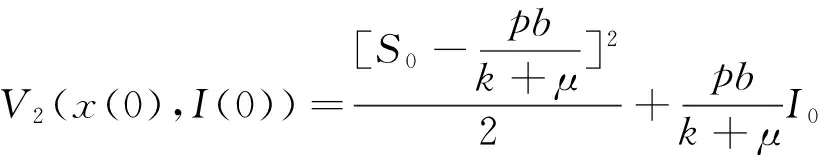
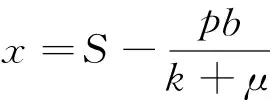
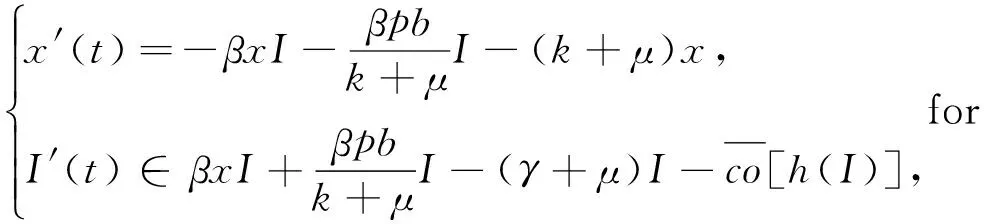
(14)

為了證明結(jié)論構(gòu)造了如下的Lyapunov函數(shù)：

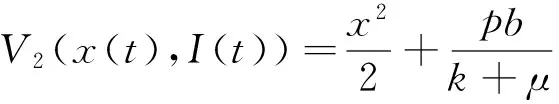
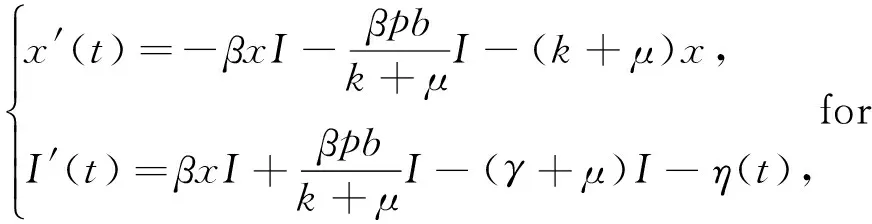
(15)

對(duì)V2(x(t),I(t))求導(dǎo)可以得到

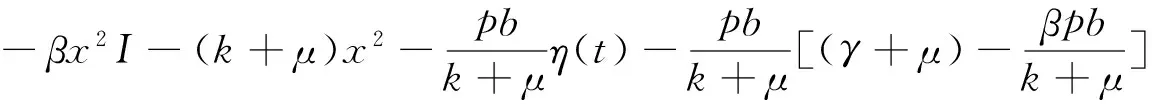
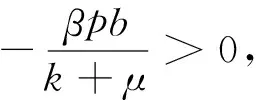
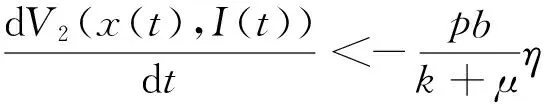
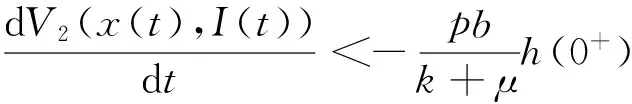
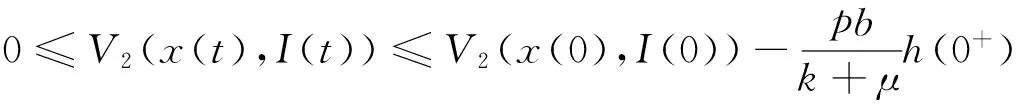
所以當(dāng)

3數(shù)值模擬

在這一節(jié)中, 將給出兩個(gè)數(shù)值分析的例子來(lái)模擬我們的理論推導(dǎo)過(guò)程.

3.1有病平衡點(diǎn)的全局收斂性

根據(jù)假設(shè)A1, 取h(I)的函數(shù)為

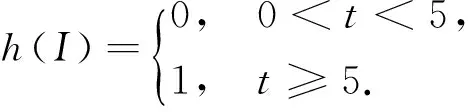
選取的參數(shù)值分別為p=0.5，b=30，β=0.2，k=0.7，μ=0.3，γ=0.2，其中S, I的初值分別為S(0)=1,I(0)=2, 得到如下結(jié)果(圖1). 從圖像中可以發(fā)現(xiàn), S(t)和I(t)都在有限的時(shí)間內(nèi)各自到達(dá)了平衡, 這和定理1得到的結(jié)果一樣.

3.2無(wú)病平衡點(diǎn)的全局收斂性

根據(jù)假設(shè)A1, 取h(I)的函數(shù)為

選取的參數(shù)值分別為p=0.2，b=2，β=0.1，k=0.6，μ=0.6，γ=0.4，其中S, I的初值分別為S(0)=1,I(0)=2, 得到如下結(jié)果(圖2). 從圖像中可以看出, I(t)在有限的時(shí)間內(nèi)滅亡, S(t)則是趨向于無(wú)病平衡點(diǎn), 這和定理2的結(jié)論是完全一致的.

圖1　地方病平衡點(diǎn)的變化趨勢(shì)圖Fig. 1　Changing trend of disease equilibrium

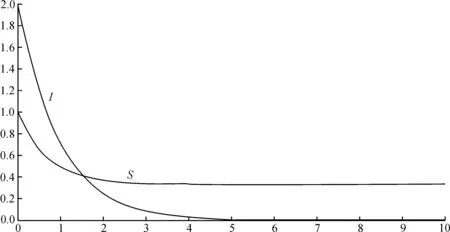
圖2　無(wú)病平衡點(diǎn)的變化趨勢(shì)圖Fig. 2　Changing trend of free disease equilibrium

4結(jié)論

在現(xiàn)實(shí)世界中由于一些人為或者自然因素的影響, 會(huì)導(dǎo)致非連續(xù)的現(xiàn)象出現(xiàn),本文得到的重要結(jié)論是知道解在何時(shí)到達(dá)平衡點(diǎn), 由此將非連續(xù)的微分理論推廣運(yùn)用到其他領(lǐng)域中去是非常有意義的, 比如傳染病系統(tǒng)、生態(tài)系統(tǒng)等. 研究非連續(xù)方程最大的困難就在于經(jīng)典微分的一些結(jié)論不能運(yùn)用到非連續(xù)微分方程中去，為了解決這一難題就需要引入Filippov解及微分包含等知識(shí)，運(yùn)用這一套方法就可以研究很多領(lǐng)域內(nèi)的非連續(xù)現(xiàn)象, 從而能夠得到更多符合實(shí)際的結(jié)論.

參考文獻(xiàn):

[1] ZOU C C, GONG W, TOWSLEY D. Code red worm propagation modeling and analysis[C]// Proceedings of the 9th ACM conference on computer and communications security. ACM,2004:138-147.

[2] DATA S, WANG H. The effectiveness of vaccinations on the spread of email-borne computer viruses[C]//IEEE CCECE/CCGEI. Saskatoon,2005:219-223.

[3] KEPHART J O, WHITE S R. Directed graph epidemiological model of computer virus[C]//Proceedings of the 1991 IEEE Symposium on Security and Privacy. Washington DC: IEEE Computer Society,1991:343-359.

[4] BLYUSS K B, KYRYCHKO Y N. Stability and bifurcations in an epidemic model with varying immunity period[J]. Bulletin of Mathematical Biology,2010,72(2):490-505.

[5] ZOU C C, TOWSLEY D, GONG W B. On the performance of Internet worm scanning strategies[J]. Performance Evaluation,2006,63(7):700-723.

[6] 肖麗，包駿杰，馮麗萍．一種新的計(jì)算機(jī)病毒模型的穩(wěn)定性分析[J]．湘潭大學(xué)自然科學(xué)學(xué)報(bào)，2012，34(2)：94-96．

[7] ZHANG D X, DING W W, ZHU M. Existence of positive periodic solutions of competitor-competitor-mutualist Lotka-Volterra systems with infinite delays[J]. Journal of Systems Science & Complexity,2015,28(2):316-326.

[8] ZHANG D X, DING W W, ZHOU W. Existence of positive periodic solution of delayed Gilpin-Ayala competion systems with discontinuous harvesting policy[J]. Journal of Anhui Normal University,2014,37(6):515-519.

[9] FILIPPOV A F. Differential equations with discontinuous righthand sides[M]. The Netherlands :Kluwer Academic Publishers Group,1998.

[10] AUBIN J P,CELLINA A. Differential inclusion:set-valued and viability theory[M]. Berlin: Springer-Verlag,1984.

[11] FORTI M, GRAZZINI M, NISTRI P, et al. Generalized Lyapunov approach for convergence of neural networks with discontinuous or non-Lipschitz activations[J]. Physica D Nonlinear Phenomena,2006,214(1):88-99.

收稿日期：2015-09-25

基金項(xiàng)目：國(guó)家自然科學(xué)基金項(xiàng)目(11302002).

通信作者：張道祥 (1979-),男,副教授,博士,主要從事應(yīng)用數(shù)學(xué)研究.E-mail:18955302433@163.com

doi:10.3969/j.issn.1674-232X.2016.04.013

中圖分類(lèi)號(hào):O175；Q141MSC2010：39A30；65D25

文獻(xiàn)標(biāo)志碼:A

文章編號(hào):1674-232X(2016)04-0408-07

Impact of Discontinuous Immunization Strategy on A SIR Computer Virus Model

LI Xun, ZHANG Daoxiang, ANG Rongrong

(School of Mathematics and Computer Science, Anhui Normal University, Wuhu 241002, China)

Abstract:In this paper, a discontinuity on the right computer virus model was studied. The basic reproduction number R0 was obtained by calculating. With the knowledge of differential calculus, the Filippov solution for the model was defined, the existence and uniqueness of the equilibrium of the model were proved. By constructing Lyapunov function, it was proved that each solution was global convergence to the disease equilibrium in finite time when R0>1, while each solution was global convergence to the free disease equilibrium in finite time when R0>1. Some numerical simulations were also carried out to illustrate the theoretical results with MATLAB.

Key words:computer virus; discontinuous immunization strategy; Lyapunov function; finite time global convergence