關于二元冪等矩陣多項式的群逆

余立婷，杜乃林

(武漢大學數學與統計學院, 湖北 武漢 430072)

?

關于二元冪等矩陣多項式的群逆

余立婷，杜乃林

(武漢大學數學與統計學院, 湖北 武漢 430072)

摘要：利用冪等矩陣和核空間的性質, 討論了復數域上兩個冪等矩陣P和Q在條件(PQ)n=(PQ)nP下的一類矩陣多項式的秩和群逆的相關問題, 并且得到了其可逆的一些充要條件.

關鍵詞：群逆; 冪等矩陣; 可逆性

0引言與記號

近年來,冪等矩陣多項式在代數學和統計學中出現了一些令人關注的應用,引發了人們對這種形式的矩陣加以研究的興趣,特別是對這類矩陣的秩和群逆(包括逆)的研究工作得到了較多的結果[1-14].

考慮復數域上兩個p階冪等矩陣P和Q(P2=P,Q2=Q)的常數項為零的m次多項式,其一般規約形式為

T=x1P+y1Q+x2PQ+y2QP+…+xm(PQ)kmPδm+ym(QP)kmQδm,

其中km,δm都是非負整數,滿足2km+δm=m且0≤δm<2.本文研究形如T這類矩陣的群逆及其相關問題,意在把前人的工作推廣到一個統一的結果.

讓我們回顧這方面的已有主要結論.2004年,文獻[1]證明了T=x1P+y1Q可逆的充要條件是P-Q可逆.2006年,文獻[2]得到了T=x1P+y1Q的秩與系數x1,y1的選取無關.在此基礎上,2010年,文獻[3]研究了矩陣多項式T=x1P+y1Q+x2PQ在一定條件下的秩與系數的關系,推廣了前人的結果.2014年,文獻[4]在冪等矩陣P,Q滿足PQP=PQ的條件下,得到了T=x1P+y1Q+x2PQ+y2QP的群逆的具體表達式.文獻[5]給出了分別在條件(PQ)2=(QP)2以及(PQ)2=0下,T=x1P+y1Q+x2PQ+y2QP+x3PQP+y3QPQ+x4(PQ)2的群逆和可逆的充要條件.2013年,文獻[6]在Hilbert空間上,得到了在條件(PQ)2=(PQ)2P下,T=x1P+y1Q+x2PQ+y2QP+…+x4(PQ)2+y4(QP)2可逆的一些充要條件,給出了群逆存在的條件,推廣了前人的結論.

復數域上冪等矩陣P,Q在條件(PQ)n=(PQ)nP下構成的這種矩陣多項式可以化簡為

T=x1P+y1Q+x2PQ+y2QP+…+x2n(PQ)n+y2n(QP)n+y2n+1(QP)nQ.

(1)

簡單計算可知冪等陣P,Q在滿足(PQ)n=(PQ)nP時包括以下的特殊情形:

(i)PQP=PQ(參見文獻[4]);

(ii)(PQ)2=(QP)2,或(PQ)2=0(參見文獻[5]);

(iii)(PQ)2=(PQ)2P(參見文獻[6]);

(iv)(PQ)n=(QP)n或(PQ)n=0.

本文研究了復數域上的冪等矩陣P,Q在條件(PQ)n=(PQ)nP下所構成的矩陣多項式(1)的秩與系數的關系,并且得到了(1)可逆的一些充要條件,也證明了其群逆存在.前人分別在條件(i)-(vi)下討論P,Q所構成的矩陣多項式的群逆及其逆的相關問題,由以上討論可知本文把前人的工作推廣到了一個統一的結果.

文章采用以下記號:Cp×p為全體p×p階復矩陣的集合,對任一A∈Cp×p,R(A)表示A的值域,N(A)表示A的核空間,rank(A)表示A的秩,dim(·)表示求維數,例如dim(N(A))表示N(A)的維數.若存在X∈Cp×p使得

XAX=X,AXA=A,AX=XA

成立,則稱X是A的群逆,記為A#.若其存在,則它是唯一的.注意,A#存在當且僅當rank(A)=rank(A2).群逆的相關性質可參考文獻[15].用P表示Cp×p上所有冪等矩陣的集合,即

P={P|P2=P}.

1主要結果

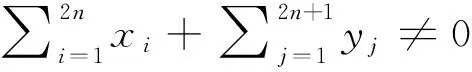
(a)rank(T)是一個常數與系數的選取無關;

(b)T的群逆存在;

(c)T可逆?P+Q可逆?N(P)∩N(Q)={0}.

證明(a)先證N(T)=N(P)∩N(Q).首先,顯然有N(P)∩N(Q)?N(T).其次,設?α∈N(T),由于冪等陣P和Q滿足(PQ)n=(PQ)nP,在等式兩邊分別乘以P,Q,可以推出

(PQ)k=(PQ)kP=(PQ)n=(PQ)nP,k≥n,

(2)

(QP)l=(QP)lQ=(QP)n+1=(QP)nQ,l≥n+1.

(3)

在式(1)兩邊左乘(PQ)n,利用(2)式得

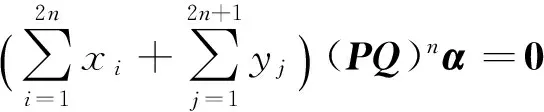
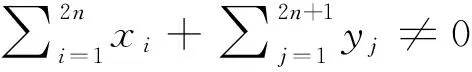
(PQ)nα=0.

(4)

在式(1)兩邊左乘(PQ)n-1P,結合式(2),式(4)可得x1(PQ)n-1Pα=0,由于系數x1≠0,因此

(PQ)n-1Pα=0.

(5)

以此類推,在式(1)兩邊分別依次左乘(PQ)n-1,(PQ)n-2P,(PQ)n-2,…,PQ,P,并利用式(2)和已得到的結果可推出

(PQ)nα=(PQ)n-1Pα=…=(PQ)2α=PQα=Pα=0.

(6)

在式(6)兩邊左乘Q,得

(QP)nQα=…=QPα=0,

(7)

再結合α∈N(T)以及式(6),(7)得Qα=0.

綜上可知,α∈N(P)∩N(Q),N(T)?N(P)∩N(Q).從而

N(T)=N(P)∩N(Q).

注意到

rank(T)=n-dim(N(T))=n-dim(N(P)∩N(Q))

是一常數,于是rank(T)與系數的選取無關.因此結論(a)成立.

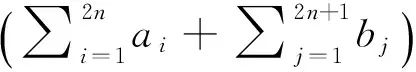
rank(T2)=rank(T).

從而T的群逆存在,(b)得證.

(c)特別地,取x1=1,y1=1,xi=0,yj=0(2≤i≤2n,2≤j≤2n+1)或者x1=1,y1=1,x2=-1,xi=0,yj=0(3≤i≤2n,2≤j≤2n+1)，則

rank(T)=rank(P+Q)=rank(P+Q-PQ).

并且利用結論(a)表明

T可逆?P+Q可逆?N(P)∩N(Q)={0}.

這樣就完成了定理1的證明.

文獻[4-6]中的主要結果可以利用定理1的結論簡單地推導得到,即如下推論：

推論1設P,Q∈Cp×p滿足PQP=PQ,系數x1y1≠0,x1,y1,x2,y2,x3∈C,x1+y1+x2+y2+x3≠0,則T=x1P+y1Q+x2PQ+y2QP+x3QPQ是群逆陣.

推論2設P,Q∈Cp×p滿足(PQ)2=P(QP)2,系數x1,y1,x2,y2,x3,y3,x4,y4∈C,x1y1≠0,x1+y1+x2+y2+x3+y3+x4+y4≠0,令

T=x1P+y1Q+x2PQ+y2QP+x3PQP+y3QPQ+x4(PQ)2+y4(QP)2,

則以下結論成立:

(i)T可逆?P+Q-PQ可逆;

(ii)T的群逆存在.

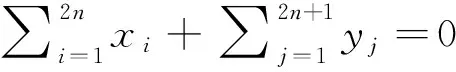
(a′)T可逆?P-Q可逆;

(b′)如果P+Q或P+Q-PQ可逆,則T的群逆存在.

證明(a′)先證N(P-Q)?N(T)?N((P-Q)2),首先,顯然有N(P-Q)?N(T).其次,設?α∈N(T),在式(1)兩邊左乘(PQ)n-1P,利用式(2)得

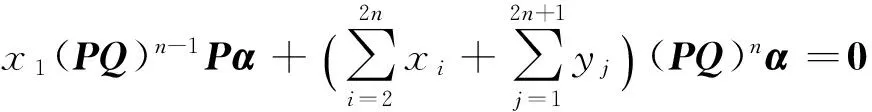
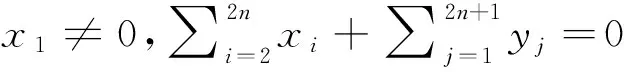
(PQ)n-1Pα=(PQ)nα.

(8)

在式(1)兩邊左乘(PQ)n-1,結合式(2)和式(8)可得

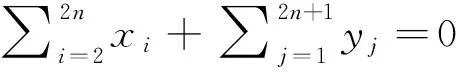
(PQ)nα=(PQ)n-1Pα=(PQ)n-1α.

(9)

以此類推，在式(1)兩邊分別依次左乘(PQ)n-2P,(PQ)n-2,…,PQ,P并利用式(2)和已得到的結果可推出

(PQ)nα=(PQ)n-1Pα=…=PQα=Pα.

(10)

在式(10)兩邊左乘Q可得

(QP)nQα=(QP)nα=…=QPQα=QPα.

(11)

(QP)nQα=(QP)nα=…=QPα=Qα.

(12)

另外由(P-Q)2α=Pα-PQα-QPα+Qα=0,所以N(T)?N((P-Q)2),從而

N(P-Q)?N(T)?N((P-Q)2).

因此

T可逆?P-Q可逆,

結論(a′)成立.

(b′)對?α∈N(T),利用式(10)和(12)可得

(P+Q)(P+Q)α=Pα-PQα+QPα-Qα=0,

(P+Q-PQ)(P-Q)α=Pα-PQα+QPα-Qα-PQPα+PQα=0.

如果P+Q或P+Q-PQ可逆,則N(P-Q)?N(T)?N(P-Q),所以

N(T)=N(P-Q)

又因為

rank(T)=n-dim(N(T))=n-dim(N(P-Q))

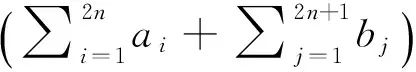
rank(T2)=rank(T).

從而T的群逆存在,(b′)得證.

文獻[4-7]中的主要結果可以利用定理2的結論簡單地推導得到,即如下推論.

推論3設P,Q∈Cp×p滿足(PQ)2=P(QP)2,系數x1,y1,x2,y2,x3,y3,x4,y4∈C,x1y1≠0,x1+y1+x2+y2+x3+y3+x4+y4=0,令

T=x1P+y1Q+x2PQ+y2QP+x3PQP+y3QPQ+x4(PQ)2+y4(QP)2,

則以下結論成立:

(i)T可逆?P-Q可逆;

(ii)如果P+Q或P+Q-PQ可逆,則T的群逆存在.

在上述結果的基礎上.我們自然想到,在(PQ)n=(PQ)nP的情況下,P,Q這類多項式T的群逆能否用P和Q及其乘積表示.根據文獻[15]表明,存在一個多項式q(x)使得T#=q(T),因為(PQ)n=(PQ)nP,這時T#仍是形如式(1)的矩陣多項式.文獻[7]給出了在(PQ)2=(PQ)2下T#的具體表達式,而此時的計算量已經非常大了,所以在探討(PQ)n=(PQ)nP的情況下,T#的表達式是一個有挑戰性的問題.

參考文獻:

[1] BAKSALARY J K, BAKSALARY O M. Nonsingularity of linear combinations of idempotent matrices[J]. Linear Algebra and Its Applications,2004,388(5):25-29.

[3] ZUO K Z. Nonsingularity of the difference and the sum of two idempotent matrices[J]. Linear Algebra and its Applications,2010,433(2):476-482.

[4] ZUO K Z, XIE T. The group inverse of the combinations of two idempotent matrices[J]. Journal of Mathematics,2014,34(3):497-501.

[5] DENG C Y. On the invertibility of Hilbert space idempotents[J]. Acta Mathematica Scientia March,2014,34(2):523-536.

[6] WANG S Q, DENG C Y. The group inverse of the combinations of two idempotent operators[J]. Abstract and Applied Analysis,2013,2013(4):1-6.

[7] LIU X J, WU L L, YU Y M. The group inverse of the combinations of two idempotent matrices[J]. Linear and Multilinear Algebra,2011,59(1):101-115.

[8] ZUO K Z, XIE T. Nonsingularity of the combinations of two orthogonal projectors[J]. Wuhan University Journal of Natural Sciences,2012,17(1):7-11.

[9] DENG C Y. The Drazin inverses of products and differences of orthogonal projections[J]. Journal of Mathematical Analysis and Applications,2007,335(1):64-71.

[10] BU C J, LI M, ZHANG K Z, et al. Group inverse for the block matrices with an invertible subblock[J]. Applied Mathematics and Computation,2009,215(1):132-139.

[11] DENG C Y. Characterizations and representations of the group inverse involving idempotents[J]. Linear Algebra and its Applications,2011,434(4):1067-1079.

[12] DU H K, YAO X Y, DENG C Y. Invertibility of linear combinations of two idempotents[J]. Proceedings of the American Mathematical Society,2006,134(5):1451-1457.

[13] BENITEZ J, SARDUVAN M, üLKER S, et al. On nonsingularity of combinations of three group invertible matrices and three tripotent matrices[J]. Linear and Multilinear Algebra,2013,61(4):463-481.

[14] CAO C G, ZHANG H Y, GE Y L. Further results on the group inverse of some anti-triangular block matrices[J]. Journal of Applied Mathematics and Computing,2014,46(1):169-179.

[15] CAMPBELL S L, MEYER C D. Generalized inverses of linear transformations[M]. New York: Dover Publication,1991.

收稿日期：2015-11-26

通信作者：杜乃林(1962—)，男，教授，博士，主要從事算子廣義逆與不適定問題研究.E-mail:dunailin@aliyun.com

doi:10.3969/j.issn.1674-232X.2016.04.014

中圖分類號:O151.21MSC2010:15A09

文獻標志碼:A

文章編號:1674-232X(2016)04-0415-05

The Group Inverse of the Binary Polynomical of Two Idempotent Matrices

YU Liting, DU Nailin

(School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China)

Abstract:The group inverse and the rank of the binary polynomical of two idempotent matrices P and Q over complex field under the condition of (PQ)n=(PQ)nP are discussed by the property of the null space of idempotent matrices, and some necessary and sufficient conditions for the invertibility are obtained.

Key words:group inverse; idempotent matrix; invertibility