立足思維訓練，提升思維品質

北京新東方揚州外國語學校　韋　璐

立足思維訓練，提升思維品質

北京新東方揚州外國語學校韋璐

在小學數學教學中，如何讓學生運用數學思維進行觀察和分析，解決日常生活中的問題，這是每一個教師都值得思考的課題。新課標也明確指出，教師要培養學生應用數學的意識，將數學思維引入生活。根據日常教學的經驗，筆者發現，很多學生在解決問題時由于缺乏思維能力，導致思路混亂，邏輯不清，遇到生活中的數學問題，常常不能學以致用。如何改變這一現狀呢？筆者認為，教師要立足思維訓練，帶領學生用數學方法觀察和思考，通過邏輯和非邏輯思維，展開推理、判斷、分析，把握數學的本質。現根據教學實踐，談談對思維訓練的體會和思考。

一、著眼細小之處，發展學生有序思維

對于小學生來說，面對問題的時候容易思路混亂，摸不到重點。為什么會這樣？主要在于學生缺乏有序思維。因此，在數學教學中，教師要培養學生解決問題的能力，就需要從小處著眼，教給學生良好的思維方式，帶領學生從最基本的小問題入手，層層分析，對大問題展開有序思考，從而找到有效的解決方法。

比如，教學《圓的認識》時，我讓學生在兩個不同的位置上畫出圓。一個位置在黑板上，另一個位置在紙上，然后讓學生觀察并思考：這兩個同樣都是圓，在畫法上有什么相同的地方？學生經過動手畫圓的操作，發現畫一個圓的關鍵點：先是要確定一個圓心，也就是中心，并且要圍繞這個中心點旋轉360度，也就是畫一圈。在從中心點到這個圓圈之間，需要隔開一段距離，這個距離也就是半徑。通過這個細節的引導，學生對圓的本質屬性有了初步認知。

又如，教學《倍數和因數》時，我讓學生先寫出2的倍數，結果學生寫出了一長串：2，4，6，8，10，12，14，16…122…，就這樣，學生從2開始寫到兩位數，3位數，追問下去，學生還會寫出4位數、5位數，甚至更多。這個時候我追問學生：你能寫完2的倍數嗎？學生通過觀察和分析發現，想要表示2的倍數，是根本寫不完的。針對這樣的情況，該如何用數學術語表達出來呢？學生認為，可以用無限個、無數個來表示。既然是無限個，那么2的倍數有最小的和最大的嗎？學生分析討論后認為，2的倍數數量上是無限的。最小的這個倍數是它本身，因為是無限個，所以最大的不存在。

以上教學，教師巧妙抓住問題的核心，從小處著眼，通過有效的思維訓練，幫助學生理清了數學概念，逐步建構了有序思維的模式，大大提升了課堂教學實效。

二、著眼分層引導，發展學生深刻思維

在小學數學教學中，學生扮演著舉足輕重的主體地位，教師要重視對學生的思維培養，不能面面俱到，強求“眉毛胡子一把抓”，而是要遵循循序漸進的原則，從條件入手，分層引導，層層深入，帶領學生從感性的表象，逐步過渡到抽象的深刻思維中來。

比如，教學《分數的認識》時，我先給學生出示了一個數學情境：如果有一個大胡蘿卜，平均分給兩只兔子。每只兔子分得多少？學生根據自己的生活常識，認為每只兔子可以分到一半。一半用什么來表示呢？學生根據自己對分數的初步認知，認為一半就是分數1/2。那么這個1/2怎么來理解呢？學生根據這個例子，認識到就是將一個胡蘿卜平均分成兩份，其中的一份就是1/2。這個時候，學生并不能真正地深入理解分數。為此我又深入設計了一個問題：將一個長方形的紙對折，怎樣才能夠折出其中的1/4呢？學生通過動手操作，認為可以將一張紙平均分成四份，其中的一份就是這張紙的1/4。如果要在這張紙上涂抹出3/4怎么辦？學生根據自己對分數的理解，認為可以將長方形等分成四份，取其中的3份就是3/4。

以上教學環節，教師著眼分層引導，借助3個層次的引領，帶領學生深入探究平均分的概念，并依據平均分，將注意的要點聚焦在其中的份數上面，從而建構了分數的意義，理解了數學概念的本質，思維獲得了提升和發展。

三、立足經驗引領，發展學生系統思維

在小學數學教學中，教材編排的知識內容具有系統性。雖然有些問題看起來相似，實際上卻深入了一層。這就需要教師在教學時關注知識的系統性，深入探究知識體系，深入淺出，辯證對待學生的負遷移，從學生的已有經驗入手，進行知識的總結和運用，發展學生的系統性思維。

比如，在教學《軸對稱圖形》這個內容的時候，筆者先讓學生動手操作，通過動手折，動手畫，學生畫出如下圖形：

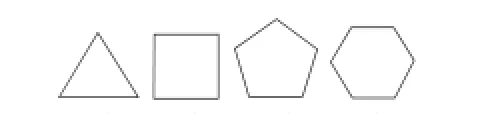
3條　4條　5條　6條

然后引導學生觀察，找出圖形當中的對稱軸，看看有幾條，發現了什么規律？學生認為，三角形有3條，正方形有4條，正五邊形有5條，正六邊形則有6條。從這個直觀的圖形當中，學生發現了一個規律：有幾條邊就有幾條對稱軸。為了驗證這一規律，我讓學生舉例。學生畫出了正八邊形，認為正八邊形就有8條對稱軸。學生還舉出了圓這個圖形，發現圓有無數條對稱軸。

以上環節，教師立足學生已有經驗，讓學生透過表象深入思考，針對表象規律進行驗證，從而有了深刻的認知。

總之，數學課堂教學的本質，是要培養學生解決問題的能力，提高學生的思維能力。因此，教師要加強思維訓練，立足培養學生的數學素養，推進高效課堂的進展。?