淺析化歸思想在高中數學教學中的應用

許世林（重慶市南坪中學校）

淺析化歸思想在高中數學教學中的應用

許世林
（重慶市南坪中學校）

化歸思想指的是將未知轉化為已知，將難化易，將各種難以理解的問題轉化為已知的、熟悉的問題，以更好、更快地解決問題。在高中數學教學中，化歸思想的應用更為廣泛。結合實際，淺析化歸思想在高中數學教學中的應用。

化歸思想；高中數學；基本原則

波利亞曾經說過：“解決問題需要不斷地變換，需要一再變化它，重新敘述它，直到最后成功地找到某些有用的東西為止……”這也提示我們在解決一些復雜問題時需要掌握和善于運用一種轉化思想，即化歸思想，也就是善于將復雜的問題往容易解決的、已知的、熟悉的問題方向轉化。因數學具有的獨特特點，將化歸思想貫穿在整個問題解決和教學過程中十分重要且必要，為了更好地發揮化歸思想在數學問題解決中的作用，促使學生更好地掌握和運用化歸思想，下面筆者對化歸思想在高中數學教學中的應用加以淺析。

一、在高中數學教學中應用化歸思想的基本原則

1.熟悉化原則：把未知不熟悉的數學問題轉化為已知熟悉的數學問題，借助已經掌握的數學知識和解決方法來解決未知不熟悉的數學問題。

2.簡單化原則：有一些數學問題常常含有不少復雜繁瑣的條件，使學生看到此類問題無從下手。此時，教師應當指導學生善于提取關鍵詞，用簡潔的方式表示該數學問題想要表示的含義，便于學生找到解決問題的突破口。

二、化歸思想指導下經常采用的幾種數學方法

1.直接轉化法：將所需要解決的數學難題直接轉化為涉及基本定義、定理、公式或基本圖形的數學問題，以便于利用已經掌握的數學知識和技巧加以解決。

2.換元法：指的是把形式較復雜或者不標準的方程、不等式、函數化歸為形式較簡單易于解決的基本問題。

3.坐標法：這種方法也比較常見，即在掌握平面圖形或者空間幾何圖形實際情況的基礎上，畫出平面的直角坐標系或空間的直角坐標系，采用坐標的形式表示平面圖形或者空間幾何圖形的各個點，借助已經掌握的坐標計算法將所需要的數量關系表示出來。在數學問題的解決中，最常見的就是借助直角坐標系把幾何問題轉化為向量問題或者代數問題。值得注意的是，這種方法需要學生具有較強的運算能力。

4.類比法：指的是借助類比推理把未知的不熟悉的問題類比為已知的、已經解決的簡單問題，化難為易。例如，等差數列類比、等比數列類比、三種圓錐曲線性質之間的類比等。

三、化歸思想在高中數學教學中應用的基本類型

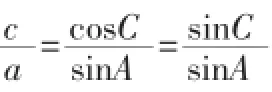
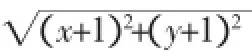
總之，在高中數學教學過程中，教師應當注重借助具體的數學問題使學生感受到化歸思想在某些數學問題解決中的重要作用，指導學生掌握將化歸思想應用于數學問題解決中的方法，以促使學生形成良好的數學思維、提高學生解決數學問題的能力。

靳世杰.高中數學化歸思想教學之我見［J］.數學學習與研究，2014（9）：58.

·編輯 薄躍華

許世林，就職于重慶市南坪中學校，本科，研究方向為數學教育教學。