基于EEMD-多尺度主元分析的回轉支承信號降噪方法研究

楊杰，陳捷，洪榮晶，王華，封楊

（南京工業大學 機械與動力工程學院，南京，210009）

（College of Mechanical and Power Engineering， Nanjing Tech University， Nanjing 210009， China）

基于EEMD-多尺度主元分析的回轉支承信號降噪方法研究

楊杰，陳捷，洪榮晶，王華，封楊

（南京工業大學 機械與動力工程學院，南京，210009）

為較好地提取故障信號，提出一種集成經驗模式分解（EEMD）和主元分析相結合的降噪方法，給出 EEMD自適應分解后本征模函數（IMF）的選擇方法，將提取出的IMF分量進行信號重構，從而達到降噪目的。將多尺度主元分析的EEMD降噪、基于峭度準則的EEMD降噪以及基于相關系數準則的EEMD降噪方法分別對仿真信號和回轉支承故障信號降噪性能進行對比。研究結果表明：基于多尺度主元分析的EEMD降噪方法具有更高的信噪比（SNR），提取出更能反映真實故障信息的特征，具有一定的實際工程應用價值。

回轉支承；主元分析；集成經驗模式分解；濾波；振動信號

（College of Mechanical and Power Engineering， Nanjing Tech University， Nanjing 210009， China）

回轉支承是連接兩大型相對回轉部件的關鍵部件，是一種承受著綜合載荷的大型滾動軸承，廣泛應用于風力發電、工程機械、海洋平臺、軍用裝備等領域。回轉支承具有不同于普通軸承的特性：其在工作中同時承受較大的軸向力、徑向力和傾覆力矩且轉速較低，通常在10 r/min以下。回轉支承在旋轉類機械中承擔著關鍵的角色，其性能影響著整個機械系統的工作狀態，因此，對回轉支承的監測和診斷具有十分重要的意義。由于回轉支承轉速低，工作環境極其惡劣，故障特征信息比較微弱，常被環境噪聲淹沒，不易識別。所以，在分析信號之前需要對信號進行有效地降噪處理，降噪的效果往往直接影響到后續的故障分析和診斷。因此，如何有效地對原始信號進行降噪，充分獲取故障信號特征，是該領域研究的熱點之一。為消除信號中的噪聲，已提出了很多方法，傳統的方法有最優濾波或最優估計方法及自適應濾波方法等，但在用這些方法時，往往需要一些先驗知識和特定假設，如噪聲類型和信號結構等。近年來，隨著小波理論的不斷發展，小波降噪技術已在信號降噪方面取得了一定的進展。LIN等［1］提出了一種基于Morlet小波基的連續小波變換降噪方法，并指出利用該方法可以從含有大量噪聲的齒輪箱振動信號中完整地識別出周期性沖擊信號。李富才等［2］將小波降噪技術引入到機械設備早期故障診斷中，取得了良好的效果。陳志新等［3］提出了一種復小波塊閾值降噪法，提取弱故障特征信息。曾慶虎等［4］提出了以一種小波相關濾波法的滾動軸承早期故障診斷方法，取得了一定的效果。孟宗等［5］提出了一種小波改進閾值去噪方法，通過仿真分析，改進后的方法比常規的小波硬閾值或軟閾值降噪效果好。但是，由于上述方法采用的都是離散小波變換，而且其降噪閾值的選取有時需要依據一定的先驗知識選取以及小波基選擇的多樣性，使得小波降噪效果受到了一定的影響。基于集成經驗模式分解（ensemble empirical mode decomposition，EEMD）的降噪方法，是一種比較有效的降噪方法。EEMD是一種完全基于數據驅動的自適應分解算法，在處理非平穩、非線性信號分解以及信號降噪處理方面要比EMD和小波等方法更有效。曹沖鋒等［6］利用EEMD分解得到的各固有模式函數（IMF）分量后，計算其與原始信號的互信息值，最后根據選擇的閾值與計算得到的互信息值來篩選IMF分量重構信號。LEI等［7］由滾動軸承振動信號經過EEMD分解后，通過計算各IMF分量的峭度偏差，根據正常和故障階段峭度偏差選擇IMF，最后通過選擇的IMF通過小波神經網絡進行軸承故障診斷。陳仁祥等［8］運用EEMD對原始信號進行分解得到一系列IMF分量后，計算各IMF分量與原始信號的相關系數，根據各 IMF的相關系數選擇較重要的IMF進行重構信號，從而達到降噪效果。胡愛軍等［9］運用EEMD對原始振動信號分解后，通過峭度準則來選取IMF分量，從而來達到降噪效果。根據文獻［6-9］研究，針對EEMD分解故障信號后不易發現含有故障信息的本征模函數（IMF）。因此，本文作者提出一種基于 EEMD和主元分析相結合的降噪方法，提供一種EEMD自適應分解后本征模函數（IMF）的選擇方法。

1　基本算法

在以上研究成果的基礎上，本文提出一種新的基于EEMD與主元故障檢測分析相結合的降噪方法。該方法結合了EEMD和主元分析（PCA）兩者的特點進行降噪，將原始信號通過EEMD自適應分解得到一系列IMF分量后，通過PCA構建主元模型來檢測各個IMF分量中是否含有故障特征信息，從而選擇含有故障信息的IMF分量進行重構原始信號。

1.1EEMD基本原理

EEMD是在經驗模式分解算法（EMD）的基礎上改進而成，其基本理論最初是由HUANG等［10］提出的一種非平穩信號分析方法。其本質是將信號從高頻到低頻分解為有限個具有物理意義的IMF及趨勢項之和。但是，在有些情況下，當利用EMD處理含有異常噪聲信號時會出現模式混疊現象，會對信號特征的識別產生不利影響，限制了其在信號降噪中的應用。為了解決模式混疊問題，WU等［11］提出了EEMD。EEMD本質是在原有信號中加入高斯白噪聲后進行多次EMD分解，在原有信號中加入白噪聲的目的是利用高斯白噪聲頻率均與分布的特性，消除原始信號中的間歇現象，從而有效地抑制模態混疊問題。對加入噪聲后的信號進行EMD后，分解得到的IMF中必然包含隨機噪聲信號，利用隨機白噪聲可以通過多次試驗相抵消的特性，通過多次EMD分解得到的IMF分量取平均就可以抑制或消除分解得到的IMF中含有噪聲的影響。EEMD算法基本步驟如下。

1） 給分析信號加入隨機高斯白噪聲序列：

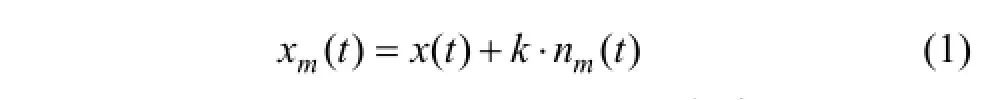
式中：x（t）為待分析原始信號；k為加入白噪聲的幅值系數；nm（t）為加入的白噪聲。

2） 將加入白噪聲的信號進行EMD分解得到1組IMF分量。

3） 重復步驟1）和2），且每次加入白噪聲的序列；

4） 計算分解到的 IMFs的總體均值，并將各個IMF的均值作為最終的結果：

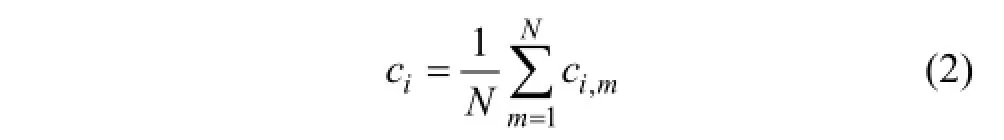
式中：ci，m為第m次EMD分解得到的第i個分量；N 為EMD分解的次數。

1.2EEMD參數設置分析

EEMD算法對信號進行分解時與EMD算法分解不同，EEMD 在分析信號時需要設置2個參數（即算法執行的總數N，以及信號中添加白噪聲序列的幅值系數K）。EEMD分解效果（即誤差e）與添加白噪聲序列的幅值系數K及執行的次數N有很大關系，其關系式定義如下：

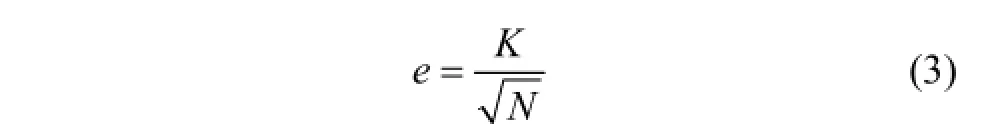
由式（3）可知：添加白噪聲的幅值系數K越小，對EEMD分解精度的提高越有利，但是當K小到一定程度時，可能不足以引起信號局部極值點的變化，從而不能改變信號的間跨度，導致信號分解的尺度變少，不能夠很好地從多個尺度了解信號。另一方面，分解次數N越大，其分解的效果也會變好，但是計算量會增加，導致 EEMD分解時間加大。因此，WU等［11］建議：添加白噪聲幅值系數K用輸入信號x（t）的標準偏差乘以1個分數來定義比較合適，這樣當分解次數N為幾百次時，殘留的噪聲引起的誤差一般處在一個較低的水平（可忽略不計）。目前，對于EEMD 分解時添加白噪聲幅值系數K以及分解次數N并沒有任何確定的公式可以運用，基本都是結合WU等［11］所提的建議來確定K和N這2個參數。因此，大多數學者建議在分解次數 N=100，添加的白噪聲幅值系數 K取0.01～0.50倍信號標準偏差時比較適宜。因為在添加的噪聲水平合適的條件下，增加分解次數對結果的改善并不顯著，只會增加運算時間，所以，在大多數情況下，分解次數N取100比較合適。

1.3主元分析基本理論

主元分析（PCA）是一種典型的數據統計分析理論，主要是將采集到的數據從高維空間投影到低維空間中，而且保留著原始數據主要的變化特征信息，最后從低維空間數據中提取相應的主元來簡化數據分析的復雜程度。假設數據樣本矩陣，每1行 Xi對應1個觀測樣本，每1列Xj對應1個變量。為了減小環境、測試系統以及數據量綱的不同對數據分析產生影響，為了使其具有客觀、統一的標準，在進行主元分析前，對數據矩陣進行標準化處理。標準化的數據矩陣X′進行奇異值分解后，數據矩陣X′分解為2部分，即

式中：X?表示X′的模型值；E表示建模誤差；T=X′P為得分矩陣；pk為主元的特征向量也稱載荷矩陣；k為主元個數。

主元個數的選取是主元分析的關鍵，主元個數選取的較多，則能更接近數據模型，得到的結果比較精確，但這樣會增大后續數據分析的復雜性。若主元個數選取得少，則不能夠充分反映原始數據信息中的主要內容。在實際應用中，主元個數的選取一般有如下3種選取方法：累積貢獻率法、能量百分比法、交叉檢驗法。采用累積貢獻率法進行選取主元個數。PCA模型建立后就可以通過測試新的數據樣本x進行過程檢測。一般用SPE圖和Hotelling T2圖進行過程檢測。觀察過程中的數據樣本是否處于平方預測誤差 SPE和Hotelling T2的控制限下，若超出控制限，則表示出現異常狀況。由于平方預測誤差 SPE統計量檢測對異常工況較T2檢測敏感，因此，采用SPE統計量進行檢測。具體算法步驟如下。

將新的數據樣本x標準化后投影到上述建立好的主元模型中后，進行如下分解：

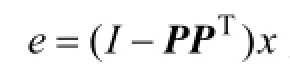
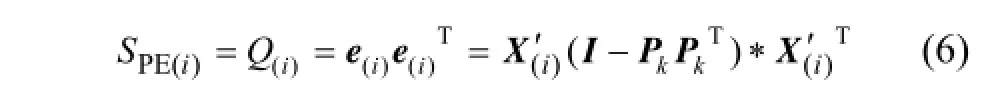
當統計指標SPE超過了正常工況時的控制限，則表明過程出現了異常。當檢驗水平為α時，其SPE的控制限可以根據式（7）計算得到：

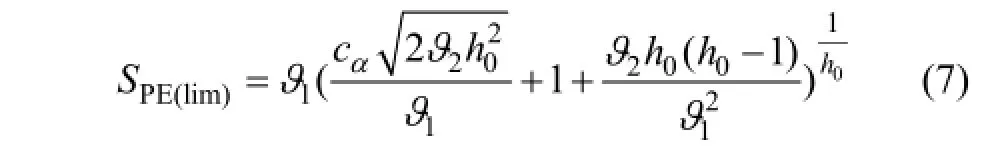
2　基于EEMD的多尺度主元降噪方法

基于 EEMD的多尺度主元分析降噪方法是將主元分析（PCA）故障檢測能力與EEMD自適應分解信號的能力相結合。該方法主要是依據MISRA等［12-14］小波多尺度分解算法改進而來，主要不同點是本文采用了 EEMD對原始信號進行自適應多尺度分解代替了小波分解。由于小波分解并非是一種自適應分解算法，在處理非線性信號時，完全依賴小波基性能。然而，EEMD是一種完全根據信號本身特性進行自適應分解的數據驅動方法。其降噪過程如圖1所示。

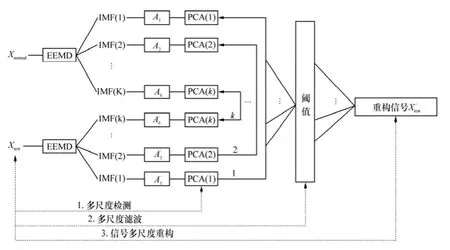
圖1　EEMD-多尺度降噪模型Fig. 1　EEMD multi-scale denoising mode

2.1正常樣本數據PCA模型建立

1） 當監測系統正常運行時，提取其相應的正常樣本數據Xnormal；

2） 將提取的數據樣本Xnormal，進行EEMD分解，得到k個不同時間尺度的IMF分量；

3） 將各個IMF分量建立相應的矩陣（A1，A2，…，Ak），對各個尺度矩陣進行主分量分析，建立正常的PCA模型，然后利用式（7）計算出其正常工況下的檢測閾值SPE（lim）。

2.2測試樣本

1） 采集監測對象的當前數據作為測試樣本Xtest。

2） 將采集得到的當前測試樣本數據 Xtest，進行EEMD分解，獲得K個不同時間尺度的IMF分量。

3） 將各個IMF分量同樣建立起相應的矩陣（A1′，A2′，…，Ak′），然后將各尺度建立起的矩陣投影到建立好的正常PCA模型，最后根據式（6）計算SPE統計量。

4） 根據計算的SPE統計值和正常樣本數據模型中計算的正常工況下的 SPE（lim）閾值進行比較。若在某個時間尺度上計算的SPE統計值超過了相應的閾值，則說明在這個尺度上存在著異常情況，極有可能是因為含有故障信息導致其超過正常工況下的閾值。

5） 將檢測出存在故障的尺度信號進行原始信號重構，從而達到降噪效果。

3　仿真信號分析

為了測試基于 EEMD的多尺度主元分析以及基于EEMD峭度準則和相關系數準則3種降噪方法對非平穩振動信號的降噪性能，進行如下仿真試驗。由于回轉支承出現故障時，故障信號非常復雜，因此，很難仿真出與真實工況下完全一致的故障信號。因此，本文以回轉支承內、外滾道出現局部故障時易產生一種周期性沖擊故障信號為特例，首先通過仿真沖擊故障信號來驗證本文提出的降噪方法的有效性和正確性。最后，通過回轉支承加速壽命試驗中，對回轉支承在真實工況下的故障信號進行降噪效果分析。根據劉永斌等［15-16］構建如下仿真信號模擬回轉支承內、外圈滾道出現局部故障時的周期性沖擊故障信號。

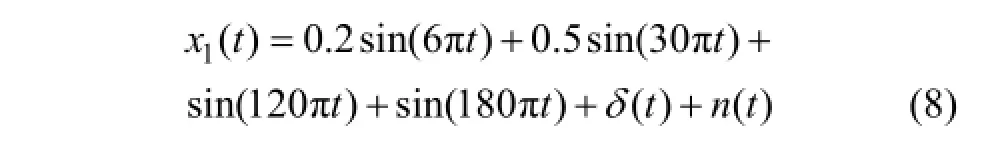
其中：n（t）為白噪聲信號；δ（t）為回轉支承滾道發生局部故障時產生的沖擊信號。

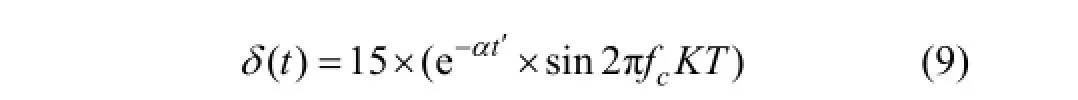
式中：

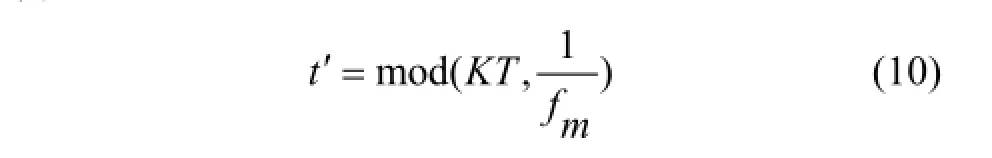
式（9）和式（10）中的指數頻率 α=800，調制頻率fm=100 Hz，載波頻率 fc=3 000 Hz，采樣間隔 T= 1/50 000。本文以式（9）為仿真故障沖擊信號，然后對其加入白噪聲信號n（t），如圖2所示。

根據本文提出的基于EEMD的多尺度檢測模型，首先將正常工況下信號（見圖 2（a））和故障信號（見圖2（b））通過EEMD分解，2次EEMD分解次數N都取100，添加的白噪聲幅值系數K為0.25，然后將分解后的信號進行多尺度主元檢測，其分析結果如圖 3～6所示。

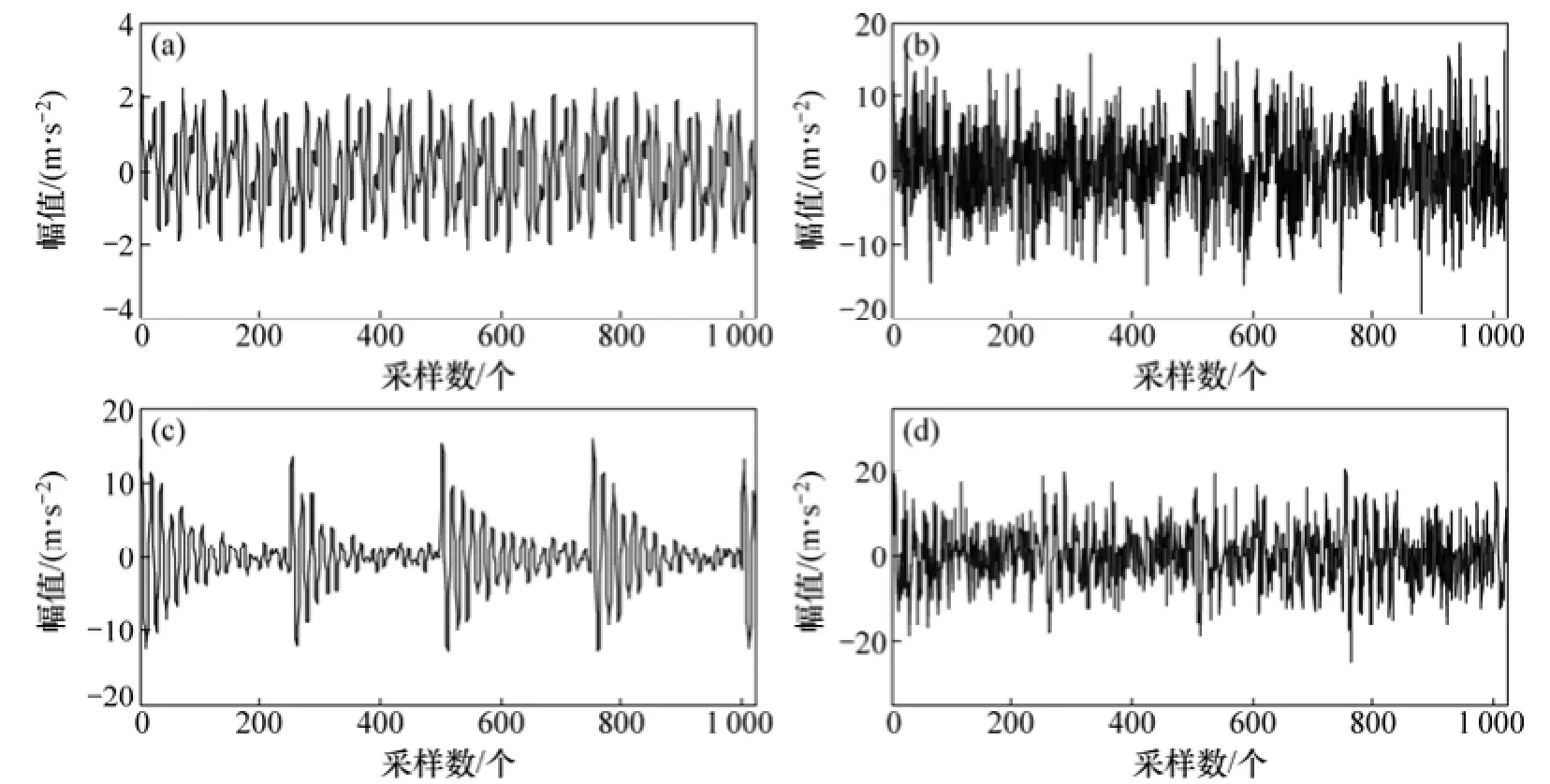
圖2　仿真振動信號波形Fig. 2　Waveforms of simulated vibration signals

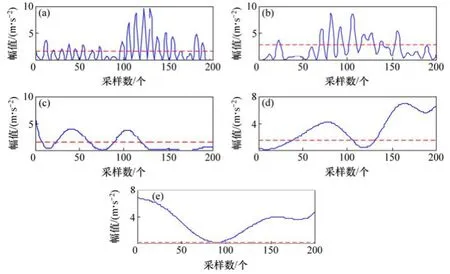
圖3　EEMD- MSPCA多尺度監測Fig. 3　EEMD-MSPCA multi-scale monitoring

含噪故障沖擊信號經過 EEMD分解得到 10個IMF分量，然后對每個IMF分量進行主元統計分析，EEMD-MSPCA多尺度監測結果如圖3所示，其中，虛線代表各 IMF分量的SPElim閾值。由圖3可知：IMF3，IMF4，IMF6，IMF7和IMF8經過PCA檢測分析后，大部分幅值超過了其正常工況下的 SPE（lim）閾值，可以判斷在以上5個IMF分量中含有故障信息。對這5個分量進行重構得到降噪后的故障信號如圖4所示。圖5所示為將降噪后信號與原始信號對比結果，可知原來淹沒在噪聲中的沖擊成分，經過EEMD-MSPCA降噪后濾除了大部分噪聲成分，使得故障沖擊特征得到體現。

3.1基于峭度準則EEMD降噪方法

峭度是描述波形尖峰度的1個量綱一參數，其數學描述為

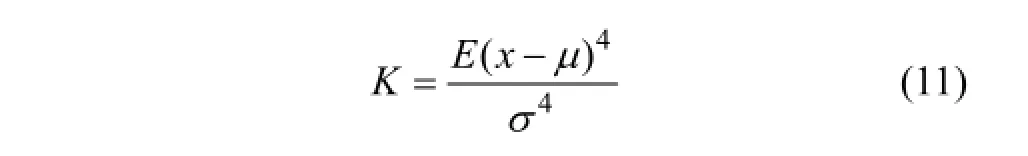
式中：μ為信號x的均值；σ為信號x的標準差。

當機械正常運行時，其振動信號近似服從正態分布，其峭度約為 3，而當機械出現故障時，信號中存在較多的沖擊成分，其峭度將明顯增大。由此可以推斷：當原始含噪故障信號經過EEMD分解且其中某些IMF分量峭度大于3時，說明這些IMF中含有較多的故障信息（即沖擊成分），具體降噪過程見文獻［9］。最后，對這些IMF進行重構，使其故障信息更加明顯，從而達到降噪效果，其降噪波形如圖6所示。

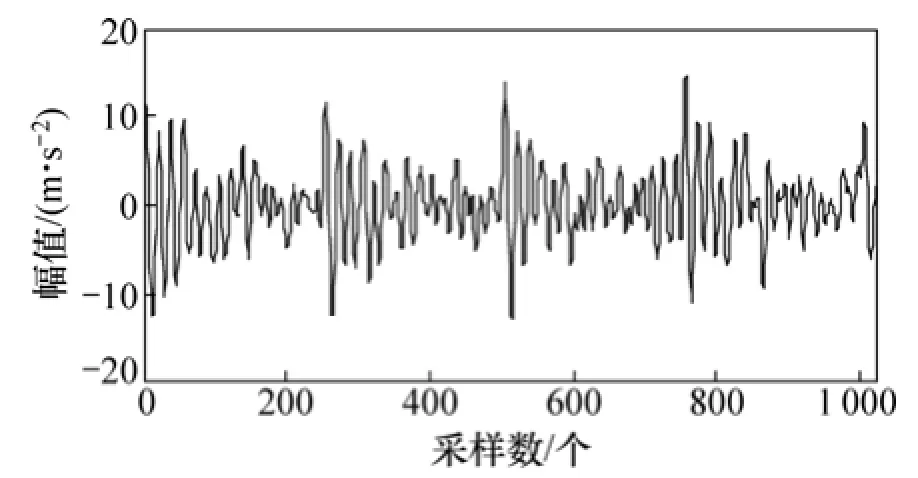
圖4　EEMD-MSPCA降噪波形Fig. 4　EEMD-MSPCA denoising waveform

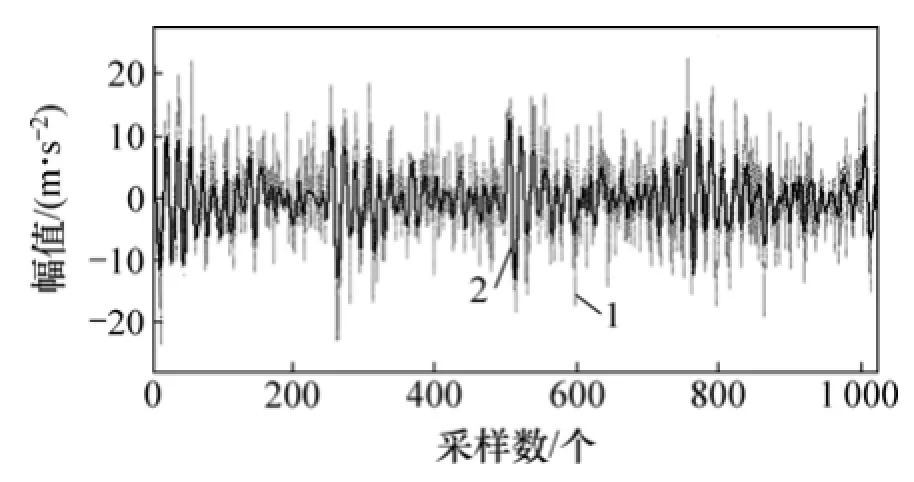
圖5　EEMD-MSPCA降噪效果Fig. 5　Effective of EEMD-MSPCA denoising

圖6　基于峭度準則信號降噪Fig. 6　Signal denoising based on kurtosis criterion

3.2基于相關系數的EEMD降噪方法

應用EEMD對信號進行降噪時，關鍵問題是IMF分量的選取方法，若IMF分量選取不當，則會導致降噪效果不佳或將有用的IMF分量去除造成有用信息丟失。基于EEMD的相關系數降噪原理主要是根據白噪聲的2個特性：1） 白噪聲與任何信號不相關，因此，白噪聲與原信號的互相關系數為0；2） 白噪聲的自相關在零點取極值，其余為0。由于 EEMD理論上是近似正交分解，而白噪聲經過近似正交分解也是趨于白噪聲。所以，可以根據EEMD分解后各尺度的IMF分量與原始信號的互相關系數和各IMF分量的自相關系數，判斷每1層IMF分量是信號還是噪聲，去除噪聲，保留信號，然后重構得到降噪后的信號。具體降噪方法見文獻［8］，其降噪效果如圖7所示。

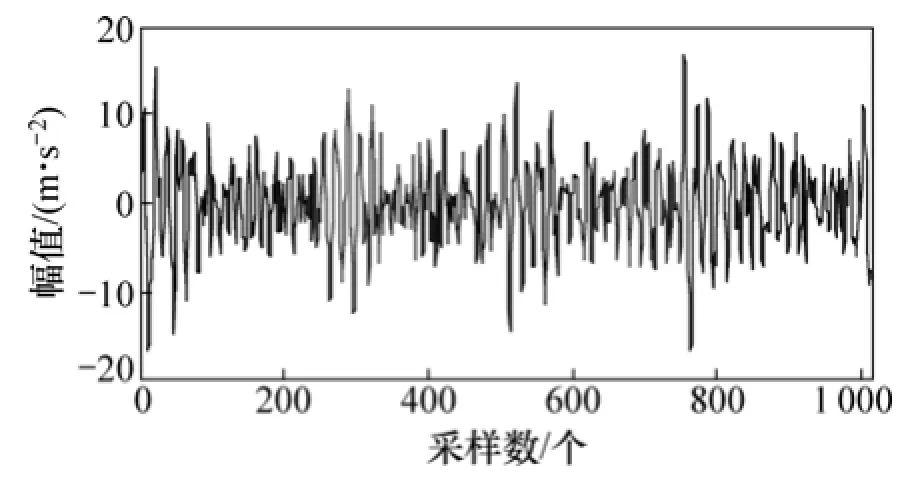
圖7　基于相關系數準則信號降噪Fig. 7　Signal denoising based on correlation coefficient criterion

對比分析圖 4、圖 6和圖 7可知：圖 4中基于EEMD-MSPCA降噪效果最好，降噪后時域波形沖擊成分較其他2種降噪方法明顯，而且圖4與圖6、圖7相比白噪聲得到了很大程度降低。對于降噪效果，除了從降噪后時域波形上進行初步分析外，最重要的是依據降噪信號的均方誤差（MSE）和信噪比（SNR）這 2個降噪指標衡量降噪效果，其定義如下：

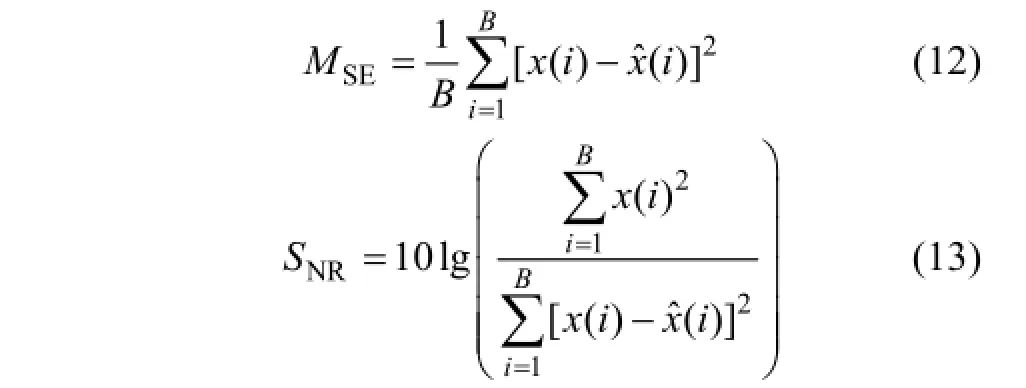
式中：MSE為均方誤差；SNR為信噪比；B為樣本數；x（i）為原始無噪沖擊信號；x?（ i）為降噪后信號。

表1所示為3種降噪方法處理后的MSE和SNR，結果表明本文提出的EEMD-MSPCA多尺度降噪方法較好地降低了均方誤差，同時提高了信噪比，從而有效地抑制噪聲，使去噪后信號更接近于原信號。

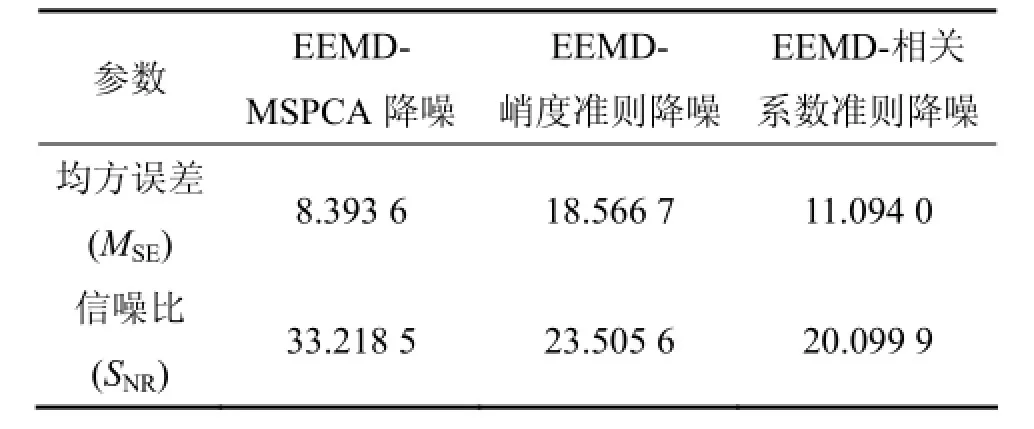
表1　降噪信號評價指標Table 1 Evaluating indicator of de-noising signals

4　工程應用

為了進一步檢驗本文提出的EEMD-MSPCA降噪方法對實際工況下回轉支承故障信號的降噪效果，將本文提出的降噪方法應用于回轉支承加速度壽命試驗中。試驗時加載的軸向力為96 kN，傾覆力矩為 246 kN·m，振動信號采樣頻率為2 048 Hz，轉速為4 r/min。為了實時地監測它的運行狀態，將4個加速度傳感器沿著90°分布安裝在回轉支承上內圈上，然后通過NI數據采集模塊對其進行數據采集。在試驗最后階段，當回轉支承外圈和滾珠都出現故障時，將此時采集的數據作為回轉支承故障樣本數據，最后對采集的數據進行離線分析。由于回轉支承轉速較低，故障信號較微弱，導致其添加的白噪聲幅值系數相對較小，其時域波形如圖 8所示。根據文獻［17］中對回轉支承故障信號進行 EEMD分解時參數選擇的經驗，本文運用EEMD算法對正常和故障樣本分解時取添加白噪聲幅值系數K=0.02，分解次數N=100，然后進行多尺度檢測，進行故障信號重構。

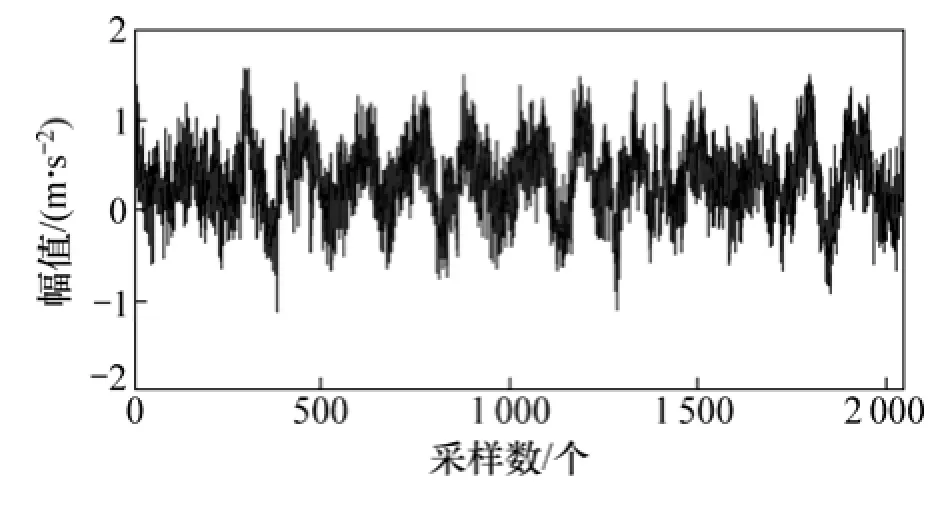
圖8　回轉支承故障原始信號波形Fig. 8　Waveform of original signals of slewing bearing

為了對比 3種降噪方法的效果，分別應用MSPCA-EEMD降噪、EEMD-峭度準則降噪及EEMD-相關系數準則降噪方法對回轉支承故障振動信號進行降噪處理，降噪結果如圖9～11所示。對比圖9～11可以看出：基于MSPCA-EEMD的時域降噪效果最好，降噪后時域波形成分基本與原始成分一致；基于EEMD-峭度準則降噪后波形出現了較小失真，不能真實地反映原始信號成分；基于EEMD-相關系數準則降噪效果沒有充分將噪聲成分濾掉，降噪效果沒有基于MSPCA-EEMD的時域降噪效果好。因此，通過仿真和回轉支承加速壽命試驗實際故障信號驗證了本文提出的基于EEMD-MSPCA多尺度降噪方法的可行性和有效性，有利于回轉支承故障特征的提取，給后續信號處理和分析帶來方便，降低噪聲對故障特征頻率的影響。

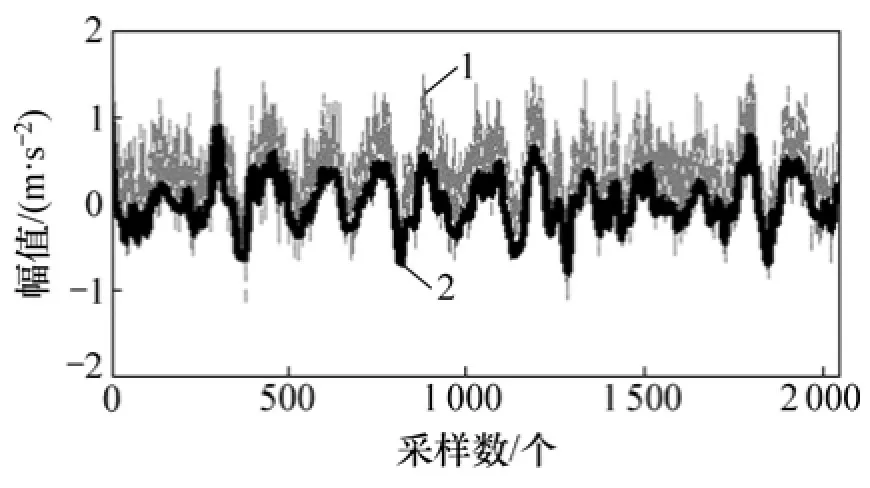
圖9　基于 EEMD-MSPCA信號降噪Fig. 9　Signal denoising based on EEMD-MSPCA

圖10　基于EEMD-峭度準則信號降噪Fig. 10 Signal denoising based on EEMD- kurtosis criterion

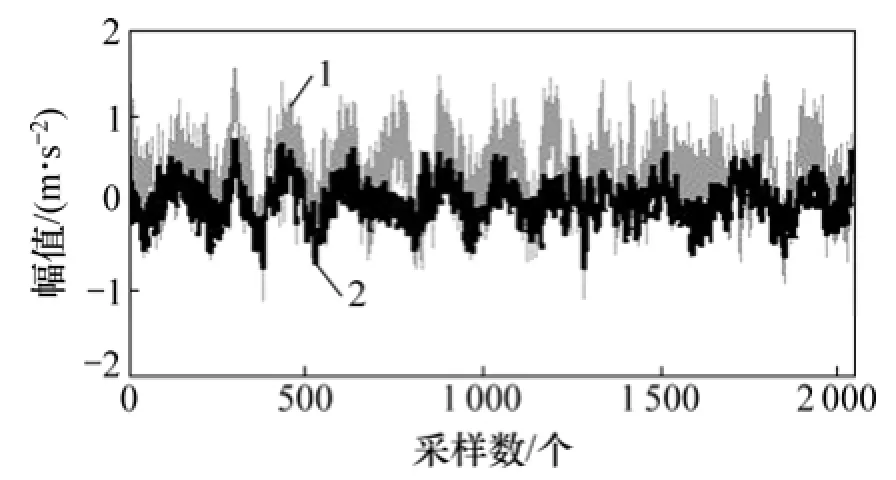
圖11　基于EEMD-相關系數準則信號降噪Fig. 11 Signal denoising based on EEMD- correlation coefficient criterion

5　結論

1） 針對機械振動信號非平穩、非線性的特性，提出一種基于EEMD的多尺度主元分析降噪方法，充分利用了 EEMD多尺度分解特性和主元分析模型可以檢測故障樣本的特點，可以獲得比基于峭度準則的EEMD降噪和基于相關系數的EEMD降噪方法更好的降噪效果。

2） 機械在運行過程中出現故障時，產生的振動信號通常較復雜，將本文提出的方法用于這些信號的降噪，不僅可以去除噪聲，而且可以充分保留故障信號中的有效成分。該方法也為機械早期故障診斷和強背景噪聲下的弱故障信息的提取提供了一種新的方法。

［1］ LIN Jing， QU Liangsheng. Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis［J］. Journal of Sound and Vibration， 2000， 234（1）： 135-148.

［2］ 李富才， 何正嘉， 陳進. 小波域相關濾波法及其早期故障預示應用［J］. 振動工程學報， 2005， 18（2）： 145-148. LI Fucai， HE Zhengjia， CHEN Jin. Wavelet transform domain correlation filter and its application in incipient fault prognosis［J］. Journal of Vibration Engineering， 2005， 18（2）： 145-148.

［3］ 陳志新， 徐金梧， 楊德斌. 基于復小波塊閾值的降噪方法及其在機械故障診斷中的應用［J］. 機械工程學報， 2007， 43（6）：200-204. CHEN Zhixin， XU Jinwu， YANG Debin. Denoising method of block thresholding based on DT-CWT and its application in mechanical fault diagnosis［J］. Chinese Journal of Mechanical Engineering， 2007， 43（6）： 200-204.

［4］ 曾慶虎， 邱靜， 劉冠軍， 等. 基于小波相關濾波法的滾動軸承早期故障診斷方法研究［J］. 機械科學與技術， 2008， 27（1）：114-118. ZENG Qinghu， QIU Jing， LIU Guanjun， et al. On incipient fault diagnosis of rolling bearings with wavelet correlation filter［J］. Mechanical Science and Technology for Aerospace Engineering，2008， 27（1）： 114-118.

［5］ 孟宗， 李姍姍. 基于小波改進閾值去噪和 HHT 的滾動軸承故障診斷［J］. 振動與沖擊， 2013， 32（14）： 204-208. MENG Zong， LI Shanshan. Rolling bearing fault diagnosis based on improved wavelet threshold de-noising method and HHT［J］. Journal of Vibration and Shock， 2013， 32（14）：204-208.

［6］ 曹沖鋒， 楊世錫， 楊將新. 大型旋轉機械非平穩振動信號的EEMD降噪方法［J］. 振動與沖擊， 2009， 28（9）： 33-38. CAO Chongfeng， YANG Shixi， Yang Jiangxin. De-noising method for non-stationary vibration signals of large rotating machineries based on ensemble empirical mode decomposition［J］. Journal of Vibration and Shock， 2009， 28（9）：33-38.

［7］ LEI Yaguo， HE Zhengjia， YAN Yangzi. EEMD method and WNN for fault diagnosis of locomotive roller bearings［J］. Expert System with Applications， 2011（38）： 7334-7341.

［8］ 陳仁祥， 湯寶平， 呂中亮. 基于相關系數的 EEMD轉子振動信號降噪方法［J］. 振動、測試與診斷， 2012， 32（4）： 542-546. CHEN Renxiang， TANG Baoping， Lü Zhongliang. Ensemble empirical mode decomposition de-noising method based on correlation coefficients for vibration signal of rotor system［J］. Journal of Vibration Measurement and Diagnosis， 2012， 32（4）：542-546.

［9］ 胡愛軍， 馬萬里， 唐貴基. 基于集成經驗模態分解和峭度準則的滾動軸承故障特征提取方法［J］. 中國電機工程學報，2012， 32（11）： 106-111. HU Aijun， MA Wanli， TANG Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion［J］. Proceedings of the Chinese Society for Electrical Engineering， 2012， 32（11）：106-111.

［10］ HUANG N E， SHEN Zheng， LONG S， et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］. Proceedings of the Royal Society of London， 1998， 454（19）： 903-995.

［11］ WU Zhaohua， HUANG N E. Ensemble empirical mode decomposition： a noise assisted data analysis method［J］. Advances in Adaptive Data Analysis， 2009， 1（1）： 1-4.

［12］ MISRA M， YUE H H， QIN S J， et al Multivariate process monitoring and fault diagnosis by multi-scale PCA［J］. Computers and Chemical Engineering， 2002， 26（9）： 1281-1293.

［13］ 鄭朝暉， 杜紅彬， 王世廣， 等. 基于Matlab的多尺度主元分析在過程監控中應用［J］. 大連理工大學學報， 2003， 43（4）：428-432. ZHEN Zhaohui， DU Hongbin， WANG Shiguang， et al. Multi-scale principal component analysis based on Matlab［J］. Journal of Dalian University of Technology， 2003， 43（4）：428-432.

［14］ 郭金玉， 曾靜. 基于多尺度主元分析方法的統計過程監視［J］.沈陽化工學院學報， 2006， 20（1）： 48-51. GUO Jinyu， ZENG Jing. Statistical process monitoring based on multi-scale principal component analysis［J］. Journal of Shenyang Institute of Chemical Technology， 2006， 20（1）： 48-51

［15］ 劉永斌. 基于非線性信號分析的滾動軸承狀態監測診斷研究［D］. 中國科學技術大學工程科學學院， 2011： 1-20. LIU Yongbin. Nonliner signal analysis for rolling bearing condition monitoring and fault diagnosis［D］. University of Science and Technology of China. School of Engineering Science， 2011： 1-20.

［16］ 蘇文盛， 王奉濤， 朱泓， 等. 雙樹復小波域隱 Markov樹模型降噪及在機械故障診斷中的應用［J］. 振動與沖擊， 2011， 30（6）：47-52. SU Wenshen， WANG Fengtao， ZHU Hong， et al. Denoising method on hidden Markov tree model in dual tree complex wavelet domain and its application in mechanical fault diagnosis［J］. Journal of Vibration and Shock， 2011， 30（6）：47-52.

［17］ WAHYU C， PRABUONO B K， ANH K T， et al. Condition monitoring of naturally damaged slow speed slewing bearing based on ensemble empirical mode decomposition［J］. Journal of Mechanical Science and Technology， 2013， 27（8）： 2253-2262.

（編輯 羅金花）

Research of slew bearing signal de-noising based on multi-scale principal component analysis and EEMD

YANG Jie， CHEN Jie， HONG Rongjing， WANG Hua， FENG Yang

In order to extract the fault signal better， a new denoising method based on multi-scale principal component analysis （MSPCA） and the ensemble empirical mode decomposition （EEMD） were proposed. Then a new intrinsic mode functions （IMFs） selection strategy was proposed， which combined the merits of ensemble empirical mode decomposition （EEMD） and principal component analysis （PCA）. Finally， vibration signal was reconstructed by the selected IMFs. In order to test the performance of the proposed denoising method， a comparison of the denoising method based on EEMD-kurtosis criterion and EEMD-correlation coefficient criterion was studied. The proposed method based on MSPCA and EEMD was validated by the simulated signals and practical fault signals of slewing bearing. The results show that the method for vibration signal filtering is more effective than other the two denoising methods. It can more effective to improve the signal to noise ratio （SNR） and extract fault characteristic information. Hence， it has powerful value for engineering application.

slewing bearing； principal component analysis； ensemble empirical mode decomposition； de-noising；vibration signal

TN911.7；TH165.3

A

1672-7207（2016）04-1173-08

10.11817/j.issn.1672-7207.2016.04.013

2015-04-13；

2015-06-20

國家自然科學基金資助項目（51375222）；國家青年科學基金資助項目（51105191）（Project （51375222） supported by the National Natural Science of China； Project （51105191） supported by the National Natural Science Foundation for Young Scientists of China）

陳捷，博士，教授，從事故障診斷與動態測試；E-mail：chenjie602604@njtech.edu.cn