非彈性結(jié)構(gòu)隨機(jī)地震反應(yīng)及概率位移需求分析實(shí)用方法

尹犟，周先雁，易偉建，陳伯望，段紹偉

（1. 中南林業(yè)科技大學(xué) 土木工程與力學(xué)學(xué)院，湖南 長(zhǎng)沙，410004；2. 湖南大學(xué) 土木工程學(xué)院，湖南 長(zhǎng)沙，410000）

非彈性結(jié)構(gòu)隨機(jī)地震反應(yīng)及概率位移需求分析實(shí)用方法

尹犟1，周先雁1，易偉建2，陳伯望1，段紹偉1

（1. 中南林業(yè)科技大學(xué) 土木工程與力學(xué)學(xué)院，湖南 長(zhǎng)沙，410004；2. 湖南大學(xué) 土木工程學(xué)院，湖南 長(zhǎng)沙，410000）

探討常規(guī)Pushover分析法的優(yōu)劣，介紹改進(jìn)后的模態(tài)Pushover分析法（即改進(jìn)MPA法）。基于概率統(tǒng)計(jì)理論和Pushover分析法的基本思想，分別推導(dǎo)2種分析多自由度結(jié)構(gòu)非彈性隨機(jī)地震反應(yīng)和概率位移需求的實(shí)用方法。方法Ⅰ采用常規(guī)POA方法將多自由度結(jié)構(gòu)等效為單自由度體系，而方法Ⅱ則主要基于改進(jìn)的 MPA法。研究結(jié)果表明：采用方法Ⅰ估計(jì)所得結(jié)構(gòu)頂點(diǎn)位移需求概率接近Monte Carlo數(shù)值模擬結(jié)果，采用方法Ⅱ估計(jì)所得結(jié)構(gòu)層間位移需求概率與概率IDA法的分析結(jié)果基本吻合。這2種方法具有準(zhǔn)確、高效且便于操作的優(yōu)點(diǎn)，與大量非線性時(shí)程分析為基礎(chǔ)的數(shù)值方法相比，其復(fù)雜程度低，運(yùn)算效率高。

非彈性結(jié)構(gòu)；隨機(jī)地震反應(yīng)；概率地震需求；位移需求

作為世界地震工程領(lǐng)域的權(quán)威研究機(jī)構(gòu)，美國太平洋地震工程研究中心（PEER）認(rèn)為［2］，基于性能的抗震工程（performance-based seismic engineering，PBSE）理論應(yīng)以概率可靠度為基礎(chǔ)，其最終分析結(jié)果應(yīng)表述為某個(gè)決策變量 DV超越某一期望值的概率。由于抗震工程領(lǐng)域存在眾多不確定因素，決策變量 DV顯然是1個(gè)隨機(jī)變量。目前估計(jì)結(jié)構(gòu)的隨機(jī)地震反應(yīng)可基于2類方法，即蒙特卡羅（Monte Carlo）數(shù)值模擬［3］和隨機(jī)振動(dòng)理論。Monte Carlo數(shù)值模擬適用性廣泛，但其分析效率很低。隨機(jī)振動(dòng)方法不需要重復(fù)進(jìn)行繁瑣的數(shù)值模擬，然而，目前這類方法大都用于分析線彈性結(jié)構(gòu)的隨機(jī)地震反應(yīng)［4-5］，僅在少數(shù)情況下適用于非線性結(jié)構(gòu)體系［6-7］，且其誤差通常很難估計(jì)。與傳統(tǒng)的抗震理念不同，PBSE理論更重視結(jié)構(gòu)在強(qiáng)震作用下的最大非線性位移反應(yīng)，即結(jié)構(gòu)的位移需求［9-11］。為此，本文作者將Pushover分析（Pushover analysis，POA）方法、隨機(jī)振動(dòng)理論、概率論以及數(shù)理統(tǒng)計(jì)方法有機(jī)地結(jié)合起來，在文獻(xiàn)［1］的研究基礎(chǔ)之上，建議幾種高效而實(shí)用的方法，用于估計(jì)多自由度體系（MDOFS，multi-degree-of-freedom systems）結(jié)構(gòu)在強(qiáng)震作用下的隨機(jī)位移反應(yīng)和概率位移需求。

1　改進(jìn)的Pushover分析方法

確定MDOFS結(jié)構(gòu)在強(qiáng)震下的非線性地震需求往往要借助于非線性動(dòng)力時(shí)程分析，該方法建模復(fù)雜，運(yùn)算成本高。近年來，出現(xiàn)一類確定結(jié)構(gòu)非彈性地震響應(yīng)的近似方法，即 POA方法［12-13］。這類方法計(jì)算簡(jiǎn)便且精度較高，在抗震領(lǐng)域得到廣泛應(yīng)用。

本文開發(fā)的實(shí)用概率方法借助 POA方法的一些基本假定，將復(fù)雜MDOFS結(jié)構(gòu)等效為1個(gè)單自由度體系SDOFS（single-degree-of-freedom system），因而其準(zhǔn)確性必然會(huì)受到POA方法自身精度的影響。研究表明［14］，常規(guī) POA方法根據(jù)結(jié)構(gòu)的一階彈性振型確定水平加載模式和形狀向量，主要適用于地震反應(yīng)以一階振型為主的結(jié)構(gòu)。為擴(kuò)大POA方法的應(yīng)用范圍，一些學(xué)者［15-16］對(duì)其進(jìn)行了改進(jìn)，其中比較有代表性的是模態(tài)Pushover分析（MPA，modal Pushover analysis）方法［17-18］和自適應(yīng) Pushover分析 （APA，adaptive pushover analysis）方法［19-20］。MPA方法可同時(shí)考慮結(jié)構(gòu)多階振型響應(yīng)，顯著提高了對(duì)結(jié)構(gòu)頂點(diǎn)位移需求的估計(jì)精度，但對(duì)結(jié)構(gòu)樓層或?qū)娱g位移需求估計(jì)結(jié)果仍然偏低。APA方法要求在每一加載步之后對(duì)結(jié)構(gòu)進(jìn)行1次振型分析，并根據(jù)振型分析結(jié)果實(shí)時(shí)調(diào)整結(jié)構(gòu)進(jìn)入非線性狀態(tài)之后的剛度矩陣和水平加載模式。該方法雖然精度很高，但其計(jì)算極繁瑣，在實(shí)際工程中應(yīng)用受到限制。毛建猛等［21］分析了MPA方法和APA方法各自的優(yōu)點(diǎn)和局限性，提出一種改進(jìn)的MPA方法。該方法明顯提高了對(duì)結(jié)構(gòu)層間及樓層位移的估計(jì)精度，且計(jì)算工作量遠(yuǎn)比APA方法的小，是一種準(zhǔn)確高效的POA方法。

綜合考慮計(jì)算效率和準(zhǔn)確性，開發(fā)實(shí)用概率方法主要基于常規(guī)POA和改進(jìn)MPA方法進(jìn)行SDOFS等效。與常規(guī)POA方法不同，改進(jìn)MPA方法［22］首先明確定義了結(jié)構(gòu)屈服點(diǎn)，并以結(jié)構(gòu)的屈服點(diǎn)為界，采用修正的振型（并非彈性振型）荷載模式分2個(gè)階段對(duì)其進(jìn)行Pushover分析。另外，改進(jìn)MPA方法基于修正后的形狀向量將多自由度結(jié)構(gòu)等效為單自由度體系，并據(jù)此換算結(jié)構(gòu)的樓層（或?qū)娱g）位移。具體操作步驟如下。

1） 建立結(jié)構(gòu)分析模型，確定結(jié)構(gòu)各構(gòu)件關(guān)鍵截面的彎矩-曲率恢復(fù)力模型。

2） 通過模態(tài)分析得到結(jié)構(gòu)各項(xiàng)彈性動(dòng)力特征參數(shù)（如基本周期T、質(zhì)量矩陣M、一階彈性振型向量Φ1等）。

3） 按一階彈性振型荷載模式Mψ1，對(duì)結(jié)構(gòu)逐級(jí)水平加載。每步加載完成后，判斷各構(gòu)件是否屈服，并據(jù)此修改各構(gòu)件及結(jié)構(gòu)的剛度矩陣。加載直至結(jié)構(gòu)倒塌（整體剛度矩陣 det|K|＜0）或到達(dá)某一極限狀態(tài)，繪出結(jié)構(gòu)的基底剪力-頂點(diǎn)位移關(guān)系曲線，并根據(jù)等能量原理將其理想化為雙折線，見圖1。定義圖1中的轉(zhuǎn)折點(diǎn)為結(jié)構(gòu)屈服點(diǎn)，該點(diǎn)分別對(duì)應(yīng)結(jié)構(gòu)基底剪力屈服值和頂點(diǎn)位移屈服值。

4） 提取結(jié)構(gòu)屈服點(diǎn)處的質(zhì)量、阻尼和剛度矩陣，再次對(duì)結(jié)構(gòu)進(jìn)行振型分析，獲取其前幾階屈服振型和振型參與系數(shù)。

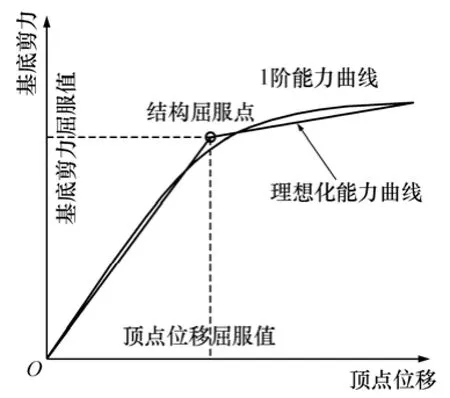
圖1　結(jié)構(gòu)屈服Fig. 1　Structural yield

5） 重新按修正的振型荷載模式 Mψi對(duì)結(jié)構(gòu)進(jìn)行Pushover分析。首先取Mi為結(jié)構(gòu)第i階彈性振型，一旦結(jié)構(gòu)達(dá)到屈服點(diǎn)，則將其修正為第i階屈服振型，并繼續(xù)加載直至結(jié)構(gòu)破壞。繪出按修正振型荷載模式加載所得結(jié)構(gòu)前幾階基底剪力-頂點(diǎn)位移關(guān)系曲線（Pushover能力曲線）。

6） 設(shè)置形狀向量初始值為結(jié)構(gòu)的前幾階彈性振型，根據(jù)式（1）將原結(jié)構(gòu)等效為幾個(gè)單自由度體系。

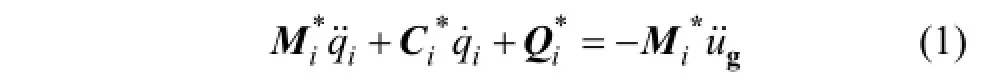
式中：參數(shù)üg為地面運(yùn)動(dòng)加速度時(shí)程和qi分別為第i階等效單自由度體系的質(zhì)量、阻尼、恢復(fù)力及位移，計(jì)算式為

ψi為結(jié)構(gòu)的第i階彈性或屈服振型向量，其取值取決于結(jié)構(gòu)是否進(jìn)入屈服狀態(tài)；I為單位向量；M，C 和Q分別為MDOFS結(jié)構(gòu)的樓層質(zhì)量矩陣、瑞利阻尼矩陣、樓層恢復(fù)力向量；uti為第i階結(jié)構(gòu)頂點(diǎn)位移；φ1i為第i階結(jié)構(gòu)頂點(diǎn)振型位移；Γi為第i階振型參與系數(shù)，）。

7） 根據(jù)非線性動(dòng)力時(shí)程分析方法，確定前幾階等效單自由度體系的地震位移需求Sdi= max|qi|，并基于式（3）將 Sdi轉(zhuǎn)換為多自由結(jié)構(gòu)的第 i階頂點(diǎn)位移需求Dti。根據(jù)事先設(shè)定的形狀向量，計(jì)算結(jié)構(gòu)第i階振型樓層位移需求和層間位移需求，并采用SRSS方法估計(jì)結(jié)構(gòu)頂點(diǎn)位移、樓層位移和層間位移需求。

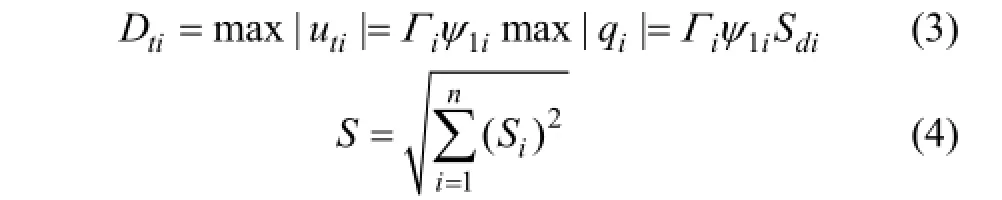
式中：Si和S分別為結(jié)構(gòu)的第i階地震效應(yīng)和前幾階地震效應(yīng)組合值。

8） 若估計(jì)所得結(jié)構(gòu)頂點(diǎn)位移需求小于其屈服值，則結(jié)構(gòu)仍處于彈性狀態(tài)，無需修正步驟6）和7）的分析結(jié)果。若不滿足上述條件，則需將形狀向量ψi設(shè)定為結(jié)構(gòu)的第i階屈服振型，并返回步驟6）開始重新迭代。

2　結(jié)構(gòu)隨機(jī)地震反應(yīng)分析實(shí)用方法

地震工程領(lǐng)域存在很多不確定因素（如地面運(yùn)動(dòng)的強(qiáng)度、持時(shí)及特征等），這些因素都會(huì)對(duì)結(jié)構(gòu)的隨機(jī)地震反應(yīng)產(chǎn)生影響，因此，結(jié)構(gòu)的最大非彈性位移反應(yīng)即結(jié)構(gòu)的非彈性位移需求必然是1個(gè)隨機(jī)變量。隨機(jī)分析的核心任務(wù)是確定隨機(jī)變量的前2階統(tǒng)計(jì)量，即均值和方差，而結(jié)構(gòu)的非彈性位移需求又是 PBSE理論關(guān)注的重點(diǎn)，因此，開發(fā)的實(shí)用方法主要用于估計(jì)MDOFS結(jié)構(gòu)非彈性位移需求的均值和方差。從理論上講，結(jié)構(gòu)地震反應(yīng)的隨機(jī)性不僅來源于地震動(dòng)，而且與結(jié)構(gòu)計(jì)算模型的不確定性有關(guān)，如結(jié)構(gòu)質(zhì)量、阻尼、剛度、強(qiáng)度等。由于這些因素的影響通常較小［23-24］，本文僅考慮地震動(dòng)隨機(jī)性對(duì)結(jié)構(gòu)位移需求的影響。

文獻(xiàn)［1］基于一種改進(jìn)的隨機(jī)地震動(dòng)模型確定了平穩(wěn)化地震隨機(jī)激勵(lì)作用下SODFS位移需求Sdp的條件概率分布函數(shù)，其先決條件為我國 GB 50011—2010“建筑抗震設(shè)計(jì)規(guī)范”規(guī)定的場(chǎng)地類別和地震分組。對(duì)上述概率分布函數(shù)求導(dǎo)即為 Sdp的條件概率密度函數(shù)：

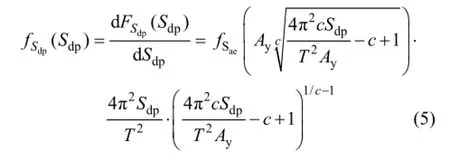
式中：fSdp（·）和fSae（·）分別為SDOFS非彈性位移需求和彈性加速度需求的條件概率密度函數(shù)，計(jì)算方法見文獻(xiàn)［1］；Sdp，Ay和T分別為SDOFS的非彈性位移需求（隨機(jī)變量）、屈服位移、特征周期；c為強(qiáng)度折減系數(shù)-延性系數(shù) （R-μ關(guān)系）回歸方程中的系數(shù)。確定了Sdp的條件概率密度函數(shù)后，運(yùn)用數(shù)理統(tǒng)計(jì)方法即可求得Sdp的均值和標(biāo)準(zhǔn)差，

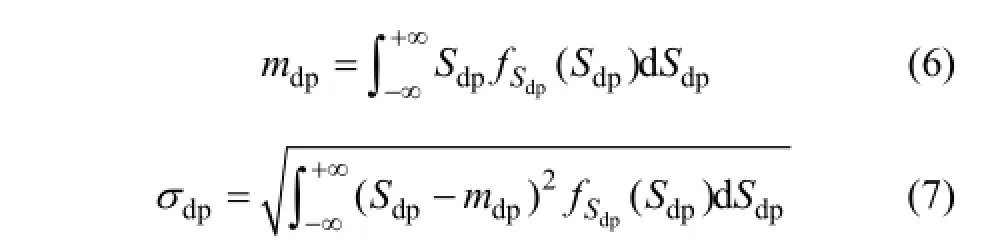
式中：mdp和σdp分別為SDOFS彈塑性位移需求Sdp的均值和標(biāo)準(zhǔn)差。實(shí)際計(jì)算時(shí)，可以將連續(xù)的隨機(jī)變量Sdp離散化，分成n個(gè)小區(qū)間，然后以求和代替積分進(jìn)行數(shù)值計(jì)算。

考慮到真實(shí)的結(jié)構(gòu)大都為多自由度體系（MDOFS），而MDOFS結(jié)構(gòu)的隨機(jī)地震反應(yīng)分析無論是理論分析還是計(jì)算均十分復(fù)雜。本文在文獻(xiàn)［1］的研究成果基礎(chǔ)上，結(jié)合常規(guī)POA方法和改進(jìn)MPA方法，建議 2種實(shí)用估計(jì)方法，用于準(zhǔn)確、高效地估計(jì)MDOFS結(jié)構(gòu)非彈性位移需求均值和標(biāo)準(zhǔn)差。

1） 建議方法Ⅰ：① 采用與結(jié)構(gòu)第一階彈性振型成比例的荷載模式，按常規(guī)POA方法對(duì)結(jié)構(gòu)進(jìn)行推覆分析；② 獲得結(jié)構(gòu)基底剪力-頂點(diǎn)位移關(guān)系曲線后，按彈性振型將原結(jié)構(gòu)等效為一單自由度體系；③ 根據(jù)式（6）和式（7）計(jì)算等效SDOFS位移需求的均值和標(biāo)準(zhǔn)差，并按式（3）將其轉(zhuǎn)換為MDOFS結(jié)構(gòu)頂點(diǎn)位移需求的均值和標(biāo)準(zhǔn)差；④ 根據(jù)所選形狀向量（一階彈性振型）將結(jié)構(gòu)頂點(diǎn)位移需求統(tǒng)計(jì)值折算為樓層或?qū)娱g位移需求的統(tǒng)計(jì)值。

2） 建議方法Ⅱ：① 按改進(jìn)MPA方法的操作步驟對(duì)結(jié)構(gòu)進(jìn)行推覆分析；② 獲得結(jié)構(gòu)基底剪力-頂點(diǎn)位移關(guān)系曲線后，按修正振型將原結(jié)構(gòu)等效為單自由度體系；③ 根據(jù)式（6）和（7）計(jì)算等效SDOFS位移需求的均值和標(biāo)準(zhǔn)差，并按式（3）將其轉(zhuǎn)換為MDOFS結(jié)構(gòu)頂點(diǎn)位移需求的均值和標(biāo)準(zhǔn)差；④ 根據(jù)修正的形狀向量（修正振型）將結(jié)構(gòu)頂點(diǎn)位移需求統(tǒng)計(jì)值折算為樓層或?qū)娱g位移需求的統(tǒng)計(jì)值。

3　結(jié)構(gòu)概率位移需求實(shí)用估計(jì)方法

概率地震需求分析的主要任務(wù)是評(píng)估結(jié)構(gòu)的地震需求參數(shù)PED在某一時(shí)間內(nèi)超過一定限值ped的概率，屬于PBSE理論框架中的核心組成部分。

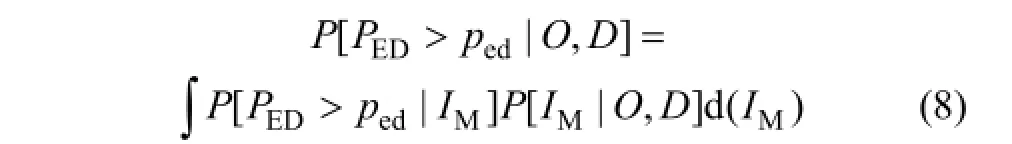
式中：O表示結(jié)構(gòu)選址的先決條件，包含場(chǎng)地的位置、地質(zhì)條件等因素；D表示結(jié)構(gòu)設(shè)計(jì)方面的先決條件；IM為地震動(dòng)強(qiáng)度指標(biāo)，受到地震動(dòng)強(qiáng)度、特征及結(jié)構(gòu)特性等因素的綜合影響。P［ IM|O， D ］為IM的條件概率；P［ PED＞ped|O， D］為在給定O和D的先決條件下，PED超過限值ped的條件概率；P［ PED＞ped|IM］為在給定IM的先決條件下，PED超過限值ped的條件概率。式（8）所示概率方程的形式也是美國太平洋地震工程研究中心（PEER）推薦的表達(dá)方式。PED可以是局部參數(shù)，如構(gòu)件的力和變形；也可以是全局參數(shù)，如結(jié)構(gòu)的頂點(diǎn)、樓層或?qū)娱g位移需求。

顯然，地震需求參數(shù)PED是1個(gè)隨機(jī)變量，其不確定性不僅來自于地震動(dòng)，而且受到結(jié)構(gòu)模型中眾多不確定性因素的影響。由于結(jié)構(gòu)模型的不確定性通常影響較小［23-25］，本文研究不予考慮。

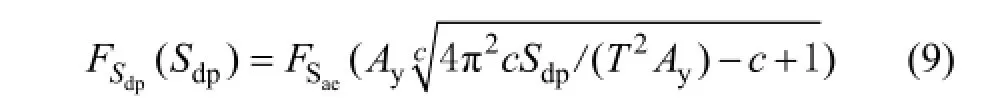
對(duì)于確定性的SDOFS，文獻(xiàn)［1］確定了其位移需求的條件概率分布模型，其先決條件為GB 50011—2010“建筑抗震設(shè)計(jì)規(guī)范”規(guī)定的場(chǎng)地類別和地震分組，為式中為 SDOFS非彈性位移需求的條件概率分布函數(shù)為SDOFS彈性加速度需求的條件概率分布函數(shù)。無論是在給定強(qiáng)度的地震動(dòng)作用下，還是在50 a設(shè)計(jì)基準(zhǔn)期內(nèi)，均可由式（9）計(jì)算SDOFS在某一超越概率下的位移需求。

考慮到真實(shí)的結(jié)構(gòu)大都為MDOFS，且MDOFS結(jié)構(gòu)概率地震需求分析的復(fù)雜程度遠(yuǎn)比單自由度體系的高。本文建議如下實(shí)用方法估計(jì)MDOFS結(jié)構(gòu)的概率位移需求，即建議方法III。研究表明［14］，雖然常規(guī)POA方法對(duì)結(jié)構(gòu)樓層或?qū)娱g位移需求的估計(jì)誤差偏大，但該方法對(duì)結(jié)構(gòu)頂點(diǎn)位移需求的估計(jì)精度尚可。由于本文算例僅涉及結(jié)構(gòu)的頂點(diǎn)位移需求，為了簡(jiǎn)化分析，建議方法III基于常規(guī)POA方法對(duì)MDOFS結(jié)構(gòu)進(jìn)行等效，具體操作步驟如下。

1） 基于常規(guī)POA方法將MDOFS結(jié)構(gòu)等效為1 個(gè)SDOFS。

2） 對(duì)于一定的超越概率F，根據(jù)式（9）分2類情況估計(jì)等效SDOFS的位移需求Sdp。

求得超越概率為F的SDOFS位移需求Sdp后，根據(jù)改進(jìn)MPA方法的操作步驟7），即可將其還原至超越概率為F的MDOFS結(jié)構(gòu)的頂點(diǎn)位移需求DF。另一方面，將Sdp除以SDOFS屈服位移xy便獲得超越概率F對(duì)應(yīng)的位移延性系數(shù)，即μ=Sdp/xy。

3） 根據(jù)一階彈性振型（即常規(guī) POA法的形狀向量），將DF折算為超越概率為F的MDOFS結(jié)構(gòu)樓層或?qū)娱g位移需求。

綜上所述，按上述步驟可以方便地確定任意超越概率F對(duì)應(yīng)的MDOFS結(jié)構(gòu)的頂點(diǎn)、樓層或?qū)娱g位移需求。另一方面，逆序執(zhí)行上述步驟亦可確定與一定位移或延性需求值相應(yīng)的超越概率F。

為了評(píng)估建議方法III的估計(jì)精度，下面算例同時(shí)列出概率增量動(dòng)力分析的結(jié)果以進(jìn)行比對(duì)。增量動(dòng)力分析（incremental dynamic analysis，IDA）方法在抗震工程領(lǐng)域得到了廣泛運(yùn)用［25-26］。對(duì)于結(jié)構(gòu)的概率地震需求分析，可采用如下方法建立概率IDA曲線：① 合理選擇結(jié)構(gòu)的關(guān)鍵地震需求參數(shù)PED即某種最大地震反應(yīng)量，如最大頂點(diǎn)位移；② 合理選擇某個(gè)參數(shù)作為地震動(dòng)的強(qiáng)度指標(biāo)IM，如地面運(yùn)動(dòng)峰值加速度APG；③ 按地震動(dòng)強(qiáng)度指標(biāo)逐步增大地面運(yùn)動(dòng)加速度記錄的強(qiáng)度，對(duì)結(jié)構(gòu)進(jìn)行動(dòng)力時(shí)程分析確定每個(gè)地震動(dòng)強(qiáng)度水平對(duì)應(yīng)的PED；④ 繪出IM和PED之間的關(guān)系曲線即為IDA曲線；⑤ 重復(fù)步驟①～④，并對(duì)所獲大量離散IDA曲線進(jìn)行統(tǒng)計(jì)分析，就能確定結(jié)構(gòu)在任意超越概率F下的IDA曲線即概率IDA曲線。概率IDA方法是一種較精確的方法，但因其計(jì)算工作量十分龐大，實(shí)際應(yīng)用受到限制。

4　算例分析

為評(píng)估本文建議實(shí)用方法的準(zhǔn)確性，選擇2個(gè)框架結(jié)構(gòu)算例進(jìn)行數(shù)值驗(yàn)證。

4.1結(jié)構(gòu)模型

結(jié)構(gòu)I：3跨7層框架結(jié)構(gòu)，8度抗震設(shè)防區(qū)（0.3g）、Ⅱ類場(chǎng)地（第2設(shè)計(jì)分組）。該框架單跨6 000 mm，底層層高4 200 mm，標(biāo)準(zhǔn)層層高3 600 mm。梁、柱混凝土為C30級(jí)，縱筋為HRB335級(jí)，箍筋為HPB300級(jí)，梁、柱截面及配筋參數(shù)見表 1，樓面及屋面荷載布置見圖2。

分別按常規(guī) POA 方法（彈性振型荷載模式）及改進(jìn) MPA方法（修正振型荷載模式）對(duì)算例結(jié)構(gòu)進(jìn)行Pushover分析。圖3所示為結(jié)構(gòu)的一階Pushover能力曲線。基于等能量原理［19］將其理想化為雙折線之后，可將原框架結(jié)構(gòu)分別等效為如下2個(gè)單自由度體系。

等效SDOFSⅠ：屈服強(qiáng)度為564 kN，屈服位移為52 mm，振型參與系數(shù)參與系數(shù)為1.29，等效質(zhì)量為430.800 t。

等效SDOFSⅡ：屈服強(qiáng)度為514 kN，屈服位移為47 mm，振型參與系數(shù)為1.38，等效質(zhì)量為385.900 t。

結(jié)構(gòu)Ⅱ：?jiǎn)螌訂慰缈蚣芙Y(jié)構(gòu)，8度抗震設(shè)防（0.2g），場(chǎng)地類別為Ⅱ類。將其成阻尼比為0.05的單自由度體系，等效質(zhì)量為200.000 t，彈性周期為1.0 s，屈服強(qiáng)度為 200 kN，采用雙線性恢復(fù)力模型（屈服后剛度系數(shù)取0.05）。

4.2本構(gòu)關(guān)系及計(jì)算方法

采用纖維梁、柱單元模擬梁柱端部截面的彎矩-曲率（轉(zhuǎn)角）非線性關(guān)系，指定鋼筋及混凝土纖維的材料本構(gòu)如下：1） 采用Kent-Park模型［27-28］模擬梁端混凝土的應(yīng)力-應(yīng)變關(guān)系骨架曲線；2） 采用改進(jìn)后的Kent-Park模型［28-29］（即Park模型）模擬柱端混凝土的應(yīng)力-應(yīng)變關(guān)系骨架曲線；3） 混凝土應(yīng)力-應(yīng)變滯回關(guān)系采用頂點(diǎn)導(dǎo)向型，見圖4（a）；4）鋼筋應(yīng)力-應(yīng)變骨架曲線采用彈性-強(qiáng)化型，滯回關(guān)系為雙線性，見圖4（b）。

結(jié)構(gòu)的振型分析、Pushover分析及動(dòng)力時(shí)程分析均采用美國南加州大學(xué)伯克利分校開發(fā)通用有限元分析程序OpenSees完成，動(dòng)力時(shí)程分析的積分步長(zhǎng)取為地面運(yùn)動(dòng)記錄時(shí)間步長(zhǎng)的1/4，采用Newmark方法進(jìn)行數(shù)值計(jì)算。

自行編寫Matlab程序完成等效SDOFS的非線性動(dòng)力時(shí)程分析，其恢復(fù)力模型為雙線性（屈服后剛度系數(shù)α=0.05），見圖4 （b）。

4.3分析結(jié)果及討論

4.3.1隨機(jī)地震反應(yīng)分析

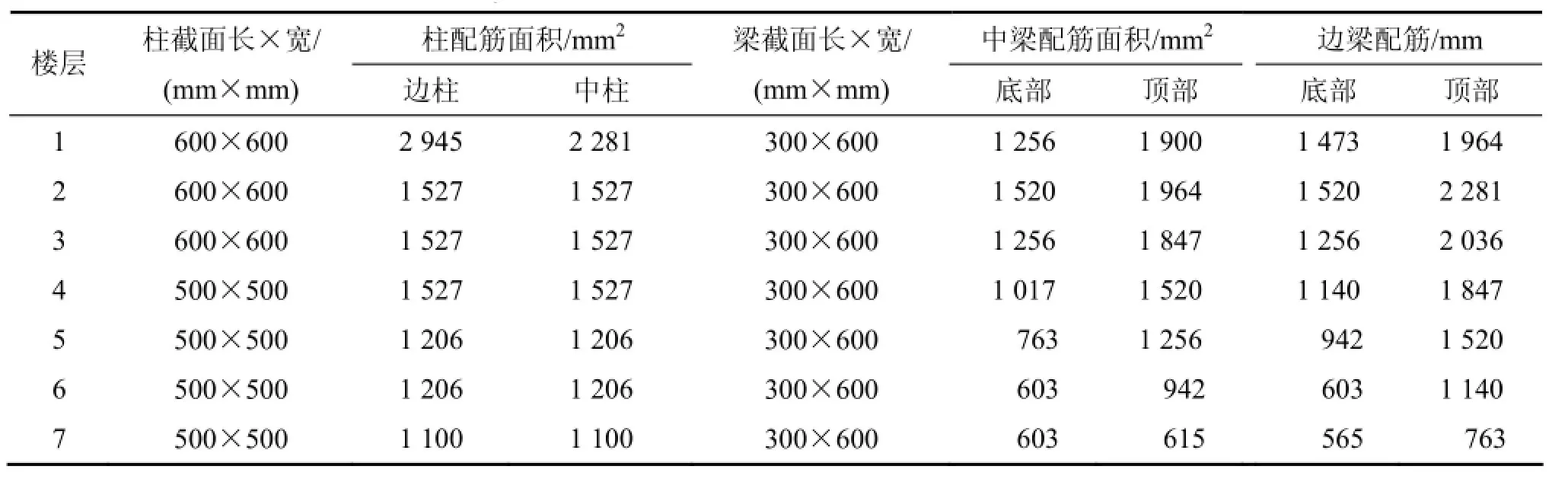
表1　7層框架梁柱尺寸及配筋面積Table 1 Geometrical properties and reinforcements schedule for beam and column of 7-storey frame

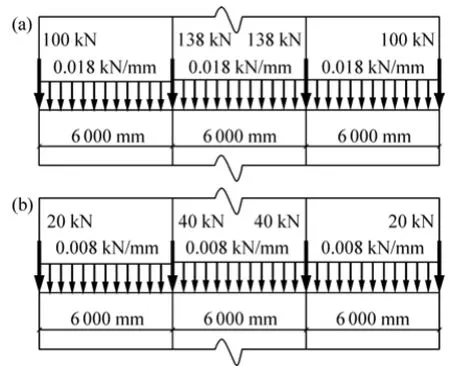
圖2　7層框架樓層受力簡(jiǎn)圖Fig. 2　Loading diagrams of 7-storey frame structure

分別采用建議方法I，Ⅱ和Monte Carlo數(shù)值方法，對(duì)7層框架結(jié)構(gòu)算例進(jìn)行隨機(jī)地震反應(yīng)分析。分析中考慮 2種情況： 工況 1（8度罕遇地震作用下，APG=5 100 mm/s2）和工況2 （50 a設(shè)計(jì)基準(zhǔn)期內(nèi)）。數(shù)值模擬采用如下步驟進(jìn)行。

圖3　7層框架1階能力曲線Fig. 3　1st order capacity curves of 7 storeys frame

工況 1：將所選Ⅱ類場(chǎng)地第2組共52條地面加速度記錄（文獻(xiàn)［1］中表2），統(tǒng)一縮放至APG=5 100 mm/s2，逐條輸入縮放后的加速度記錄進(jìn)行結(jié)構(gòu)動(dòng)力時(shí)程分析，統(tǒng)計(jì)分析全部時(shí)程分析結(jié)果即可得到算例結(jié)構(gòu)最大位移反應(yīng)（位移需求）的均值和標(biāo)準(zhǔn)差。

工況 2：由反函數(shù)法按極值Ⅱ型分布對(duì)APG進(jìn)行1 000次隨機(jī)抽樣，將所選Ⅱ類場(chǎng)地第2組共52條地面加速度記錄（文獻(xiàn)［1］中表 2），統(tǒng)一縮放至每個(gè) APG抽樣值；逐條輸入縮放后的加速度記錄進(jìn)行結(jié)構(gòu)動(dòng)力時(shí)程分析，統(tǒng)計(jì)分析全部時(shí)程分析結(jié)果即可得到算例結(jié)構(gòu)位移需求的均值和標(biāo)準(zhǔn)差。表2所示為數(shù)值方法和建議方法的計(jì)算結(jié)果。

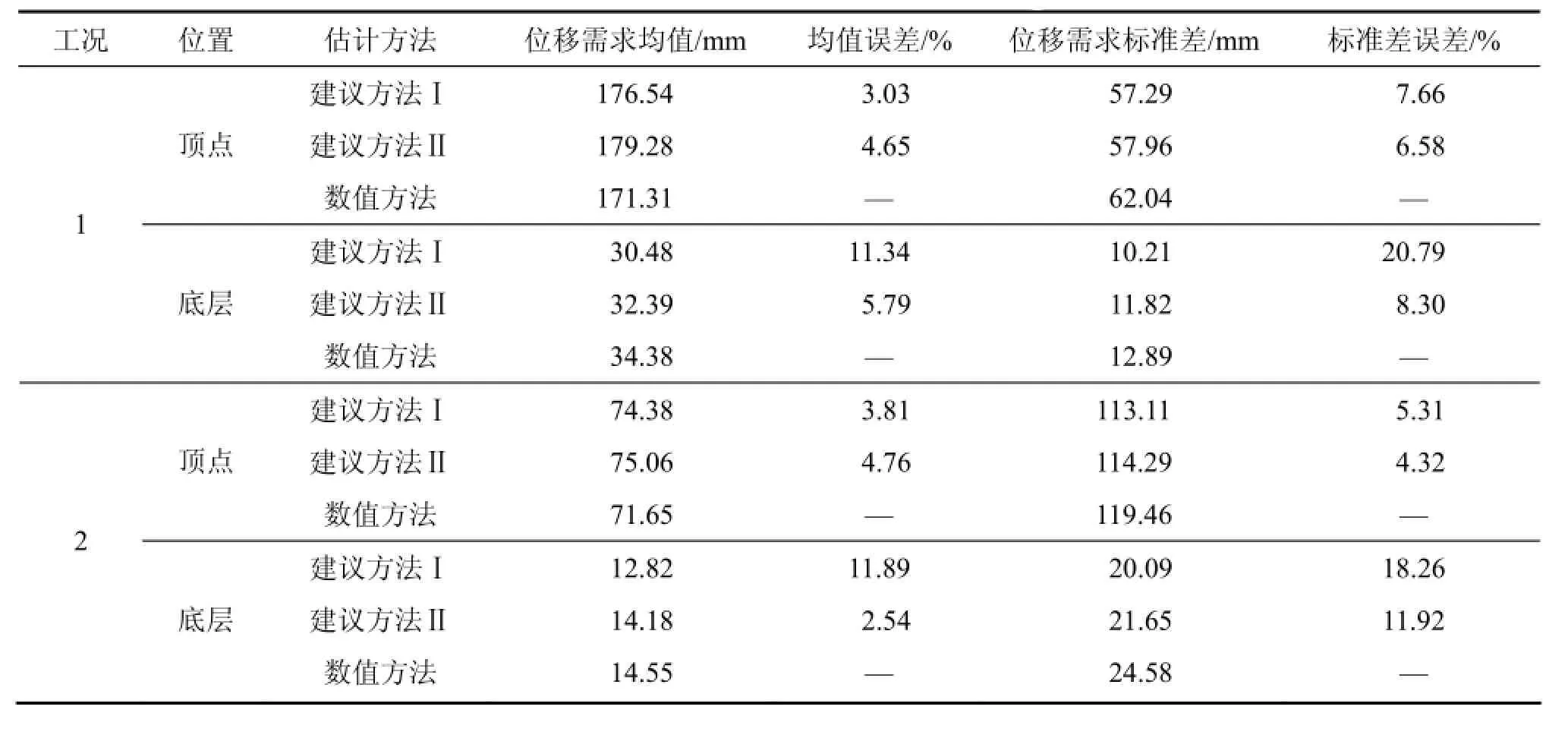
表2　7層框架頂點(diǎn)位移需求和層間位移需求的統(tǒng)計(jì)參數(shù)Table 2 Statistical parameters of roof displacement demands and inter-story drift demands for 7-story frame

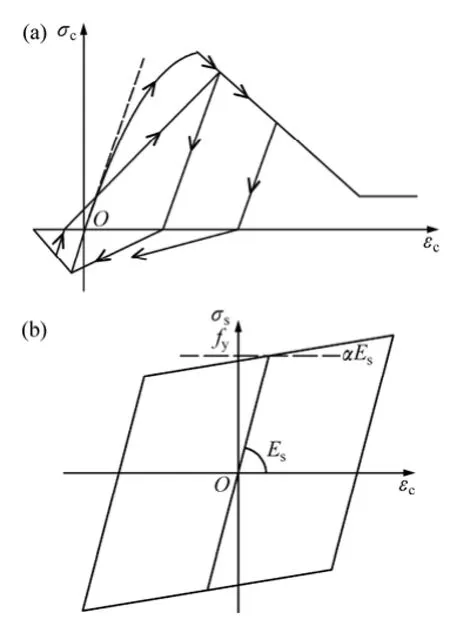
圖4　混凝土和鋼筋的材料本構(gòu)Fig. 4　Constitutive relationship of concrete and bare

由表2可知：建議方法Ⅰ對(duì)頂點(diǎn)位移需求的估計(jì)誤差較小，未超過 8%；但對(duì)層間位移需求標(biāo)準(zhǔn)差的估計(jì)誤差卻達(dá)20%左右，顯得有些偏大。究其原因在于建議方法Ⅰ采用常規(guī)POA方法對(duì)MDOFS結(jié)構(gòu)進(jìn)行等效，而常規(guī)POA方法假定結(jié)構(gòu)地震反應(yīng)始終與一階彈性振型相關(guān)，這種近似假定對(duì)于準(zhǔn)確估計(jì)結(jié)構(gòu)的頂點(diǎn)位移需求影響有限，但就估計(jì)結(jié)構(gòu)的樓層或?qū)娱g位移需求而言，其影響程度不容忽視。

與建議方法Ⅰ不同，建議方法Ⅱ基于改進(jìn) MPA方法將MDOFS結(jié)構(gòu)等效為SDOFS，在一定程度上考慮了結(jié)構(gòu)屈服后動(dòng)力特性的改變，顯著提高了對(duì)于結(jié)構(gòu)最大層間位移的估計(jì)精度（均值和標(biāo)準(zhǔn)差估計(jì)誤差均能控制在10%左右），完全可滿足工程應(yīng)用的需要。

4.3.2概率位移需求分析

在每個(gè)地震動(dòng)強(qiáng)度（APG）水平處，按建議方法 III計(jì)算2個(gè)框架結(jié)構(gòu)算例（結(jié)構(gòu)Ⅰ和結(jié)構(gòu)II ）超越概率分別為2%，50%和98%的頂點(diǎn)位移需求，計(jì)算結(jié)果見圖5中實(shí)線。與此同時(shí)，采用52條地面加速度記錄（詳見文獻(xiàn)［1］中表2）分別對(duì)2個(gè)框架結(jié)構(gòu)算例進(jìn)行IDA分析，分析結(jié)果見圖5中點(diǎn)劃線。對(duì)全部點(diǎn)劃線進(jìn)行統(tǒng)計(jì)分析即為結(jié)構(gòu)頂點(diǎn)位移需求的概率IDA曲線，見圖5中虛線。圖5所示計(jì)算結(jié)果表明：建議方法誤差較小，其分析曲線與概率IDA曲線較吻合。

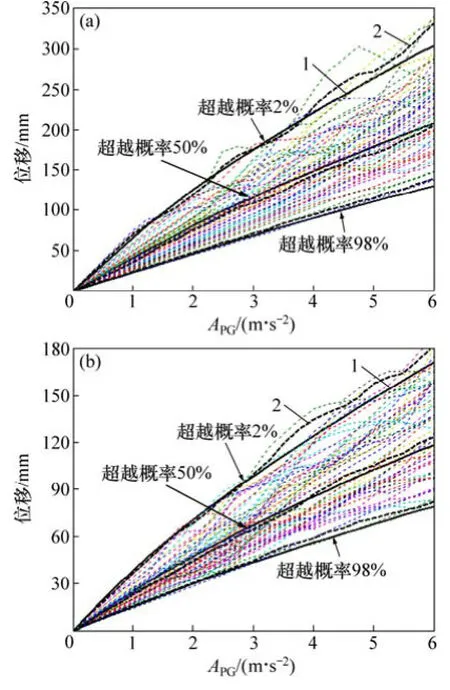
圖5　結(jié)構(gòu)頂點(diǎn)位移需求的概率IDA曲線Fig. 5　Probabilistic IDA curves of roof displacement demands for structures

采用建議方法III計(jì)算50 a設(shè)計(jì)基準(zhǔn)期內(nèi)，2個(gè)框架結(jié)構(gòu)算例頂點(diǎn)位移需求的概率分布函數(shù)。為驗(yàn)證本文方法的準(zhǔn)確性，采用Monte Carlo數(shù)值方法對(duì)建議方法III的計(jì)算結(jié)果進(jìn)行驗(yàn)證。具體實(shí)施步驟如下：1）首先根據(jù)50 a設(shè)計(jì)基準(zhǔn)期內(nèi)APG的概率分布函數(shù)（極值II型），由反函數(shù)法生成一組APG抽樣數(shù)據(jù)（1 000個(gè)）；2） 將文獻(xiàn)［1］表2中Ⅱ類場(chǎng)地第2組52條地面運(yùn)動(dòng)記錄縮放至每個(gè)APG抽樣值；3） 采用縮放后的每條地面運(yùn)動(dòng)記錄對(duì)結(jié)構(gòu)Ⅰ和結(jié)構(gòu)Ⅱ進(jìn)行動(dòng)力時(shí)程分析，并對(duì)時(shí)程分析所得結(jié)構(gòu)頂點(diǎn)位移需求進(jìn)行統(tǒng)計(jì)分析獲得其經(jīng)驗(yàn)概率分布函數(shù)。研究結(jié)果表明：本文建議方法與Monte Carlo數(shù)值方法的分析結(jié)果較吻合，但計(jì)算工作量遠(yuǎn)比Monte Carlo數(shù)值模擬的工作量小。

5　結(jié)論

1） 常規(guī)POA方法對(duì)結(jié)構(gòu)樓層和層間位移的估計(jì)誤差偏大，但對(duì)于規(guī)則框架結(jié)構(gòu)頂點(diǎn)位移的估計(jì)精度仍在工程許可的范圍內(nèi)。改進(jìn) MPA方法以結(jié)構(gòu)屈服作為分界，考慮結(jié)構(gòu)屈服后動(dòng)力特性的改變，分2階段對(duì)結(jié)構(gòu)進(jìn)行推覆分析，對(duì)結(jié)構(gòu)樓層及層間位移需求的估計(jì)精度大大提高，且計(jì)算工作量遠(yuǎn)比ASPA方法的小，是一種準(zhǔn)確、高效的POA方法。

2） 基于SDOFS地震需求的概率分布函數(shù)和概率位移譜，結(jié)合POA方法和隨機(jī)振動(dòng)理論，建議2種用于估計(jì)MODFS結(jié)構(gòu)隨機(jī)地震反應(yīng)的實(shí)用方法，該方法效率較高，精度滿足工程運(yùn)用的要求。

3） 建議一種估計(jì)非彈性MODFS結(jié)構(gòu)概率位移需求的實(shí)用方法。該方法無需進(jìn)行復(fù)雜的MODFS結(jié)構(gòu)動(dòng)力時(shí)程分析，完全采用解析方法基于理論模型估計(jì)非彈性MODFS結(jié)構(gòu)的概率位移需求，估計(jì)結(jié)果和概率IDA法的分析結(jié)果較吻合，但復(fù)雜程度以及運(yùn)算成本遠(yuǎn)比概率IDA方法的小。

［1］ 尹犟， 周先雁， 易偉建， 等. 基于改進(jìn)隨機(jī)地震動(dòng)模型的概率反應(yīng)譜［J］. 中南大學(xué)學(xué)報(bào)（自然科學(xué)版）， 2015， 46（5）：1876-1885. YIN Jiang， ZHOU Xianyan， YI Weijian， et al. The probability spectrum for seismic demand based on a improved stochastic model for earthquake ground motion［J］. Journal of Central South University （Science and Technology）， 2015， 46（5）： 1876-1885.

［2］ UMA S R， PAMPANIN S， CHRISTOPOULOS C. Development of probabilistic framework for performance-based seismic assessment of structures considering residual deformations［J］. Journal of Earthquake Engineering， 2010， 14（7）： 1092-1111.

［3］ CHEUNG S H， BECK J L. Bayesian model updating using hybrid Monte Carlo simulation with application to structuraldynamic models with many uncertain parameters［J］. Journal of Engineering Mechanics， 2009， 135（4）： 243-255.

［4］ GANJI A， JOWKARSHORIJEH L. Advance first order second moment （AFOSM） method for single reservoir operation reliability analysis： a case study［J］. Stochastic Environmental Research and Risk Assessment， 2012， 26（1）： 33-42.

［5］ 王鳳陽， 趙巖， 林家浩. 參數(shù)不確定結(jié)構(gòu)平穩(wěn)隨機(jī)響應(yīng)虛擬激勵(lì)攝動(dòng)方法［J］. 大連理工大學(xué)學(xué)報(bào)， 2011， 51（3）： 320-326. WANG Fengyang， ZHAO Yan， LIN Jiahao. Pseudo-excitation perturbation method for stationary random response of structure with uncertain parameters［J］. Journal of Dalian University of Technology， 2011， 51（3）： 320-326.

［6］ SPIGLER R， ZERBETTO R. Random perturbations effects on the stability of tension leg platforms in offshore engineering and of other large structures［J］. Applied Mathematical Modelling，2013， 37（5）： 2881-2899.

［7］ XU Jun， CHEN Jianbing， LI Jie. Probability density evolution analysis of engineering structures via cubature points［J］. Computational Mechanics， 2012， 50（1）： 135-156.

［8］ ANH N D， HIEU N N， LINH N N. A dual criterion of equivalent linearization method for nonlinear systems subjected to random excitation［J］. Acta Mechanica， 2012， 223（3）： 645-654.

［9］ PAOLUCCI R， FIGINI R， PETRINI L. Introducing dynamic nonlinear soil-foundation-structure Interaction effects in displacement-based seismic design［J］. Earthquake Spectra， 2013，29（2）： 475-496.

［10］ CALVI G M， PRIESTLEY M J N， KOWALSKY M J. Displacement-based seismic design of bridges［J］. Structural Engineering International， 2013， 23（2）： 112-121.

［11］ PANG W C， ROSOWSKY D V. Direct displacement procedure for performance-based seismic design of mid-rise wood-framed structures［J］. Earthquake Spectra， 2009， 25（3）： 583-605.

［12］ REYES J C， CHOPRA A K. Three-dimensional modal pushover analysis of buildings subjected to two components of ground motion， including its evaluation for tall buildings［J］. Earthquake Engineering & Structural Dynamics， 2011， 40（7）： 789-806.

［13］ PARASKEVA T S， KAPPOS A J. Further development of a multimodal pushover analysis procedure for seismic assessment of bridges［J］. Earthquake Engineering & Structural Dynamics，2010， 39（2）： 211-222.

［14］ KRAWINKLER H. Pros and cons of a pushover analysis of seismic performance evaluation［J］. Engineering Structures， 1998，20（6）： 452-464.

［15］ MORTEZAEI A， RONAGH H R. Effectiveness of modified pushover analysis procedure for the estimation of seismic demands of buildings subjected to near-fault ground motions having fling step［J］. Natural Hazards and Earth System Science，2013， 13（6）： 1579-1593.

［16］ JIANG Y， LI G， YANG D. A modified approach of energy balance concept based multimode pushover analysis to estimate seismic demands for buildings［J］. Engineering Structures， 2010，32（5）： 1272-1283.

［17］ REYES J C， CHOPRA A K. Three-dimensional modal pushover analysis of buildings subjected to two components of ground motion， including its evaluation for tall buildings［J］. Earthquake Engineering & Structural Dynamics， 2011， 40（7）：789-806.

［18］ KALKAN E， CHOPRA A K. Modal-pushover-based ground-motion scaling procedure［J］. Journal of Structural Engineering， 2010， 137（3）： 298-310.

［19］ PAPANIKOLAOU V K， ELNASHAI A S. Evaluation of conventional and adaptive pushover analysis I： methodology［J］. Journal of Earthquake Engineering， 2005， 9（6）： 923-941.

［20］ SHAKERI K， TARBALI K， MOHEBBI M. An adaptive modal pushover procedure for asymmetric-plan buildings［J］. Engineering Structures， 2012， 36（3）： 160-172.

［21］ 毛建猛， 謝禮立， 翟長(zhǎng)海. 模態(tài) Pushover分析方法的研究和改進(jìn)［J］. 地震工程與工程振動(dòng)， 2006， 26（6）： 49-55. MAO Jianmeng， XIE Lili， ZHAI Changhai. Studies on and improvements in modal pushover analysis［J］. Earthquake Engineering and Engineering Vibration， 2006， 26（6）： 49-55.

［22］ 尹犟. 混凝土結(jié)構(gòu)地震需求估計(jì)方法研究［D］. 長(zhǎng)沙： 湖南大學(xué)土木工程學(xué)院， 2011： 21-32. YIN Jiang. The Study of Seismic demand estimation method of reinforced concrete structures［D］. Changsha： Hunan University. Collge of Civil Engineering， 2011： 21-32.

［23］ LEE T H， MOSALAM K M. Seismic demand sensitivity of reinforced concrete shear-wall building using FOSM method［J］. Earthquake Engineering & Structural Dynamics， 2005， 34（14）：1719-1736.

［24］ PADGETT J E， DESROCHES R. Sensitivity of seismic response and fragility to parameter uncertainty［J］. Journal of Structural Engineering， 2007， 133（12）： 1710-1718.

［25］ VAMVATSIKOS D， FRAGIADAKIS M. Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty［J］. Earthquake Engineering & Structural Dynamics，2010， 39（2）： 141-163.

［26］ DOLSEK M. Incremental dynamic analysis with consideration of modeling uncertainties［J］. Earthquake Engineering & Structural Dynamics， 2009， 38（6）： 805-825.

［27］ YU Ping， ZHANG Qin， YANG Li， et al. Analysis and comparison of different confined concrete models［J］. Applied Mechanics and Materials， 2013， 438（10）： 187-193.

［28］ YOUSSEF M A， MOFTAH M. General stress-strain relationship for concrete at elevated temperatures［J］. Engineering Structures，2007， 29（10）： 2618-2634.

［29］ 周文峰， 黃宗明， 白紹良. 約束混凝土幾種有代表性應(yīng)力-應(yīng)變模型及其比較［J］. 重慶建筑大學(xué)學(xué)報(bào)， 2003， 25（4）： 121-128. ZHOU Wenfeng， HUANG Zongming， BAI Shaoliang. Introduction and comparison of several representative confinement models for concrete［J］. Journal of Chongqing Jianzhu University， 2003， 25（4）： 121-128.

（編輯 陳燦華）

Practical method for random seismic response and probabilistic displacement demand analysis of inelastic structures

YIN Jiang1， ZHOU Xianyan1， YI Weijian2， CHEN Bowang1， DUAN Shaowei1

（1. College of Civil Engineering and Mechanics，Central South University of Forestry and Technology， Changsha 410004， China；2. College of Civil Engineering， Hunan University， Changsha 410000， China）

The benefits and limitations of conventional Pushover analysis（POA） method was studied， and the basic procedure of an improved modal pushover analysis （MPA） method was proposed. Based on probability statistical theory and the baisic principle of Pushover analysis method， two kinds of practical methods were proposed for analyzing random seismic response and probabilistic displacement demand of multi-degree-of-freedom inelastic systems. For the proposed methodⅠ， the multi-degree-freedom structure is equivalent to a single-degree-freedom system by using the conventional POA method. For the proposed method Ⅱ， the improved MPA method was used. The results show that the probabilistic demands of roof displacement obtained from proposed method Ⅰare very close to that from Monte Carlo method， and the probabilistic demands of inter-story drift derived from the proposed method II are basically close to those from the probabilistic IDA （incremental dynamic analysis） method. The recommended practical methods are accurate， efficient and easy to operate， and its complexity and calculation work are far less than those of numerical methods based on a large number of non-linear time-history analysis.

inelastic structures； random seismic response； probabilistic seismic demand； displacement demand

TU311.3；TU375.4

A

1672-7207（2016）04-1338-08

10.11817/j.issn.1672-7207.2016.04.033

2015-04-10；

2015-06-12

國家林業(yè)公益性行業(yè)科研專項(xiàng)基金資助項(xiàng)目（201304504）；國家自然科學(xué)基金資助項(xiàng)目（51178175，51204215）；湖南省自然科學(xué)基金資助項(xiàng)目（13JJ5027）；教育部高等學(xué)校博士學(xué)科專項(xiàng)科研基金資助項(xiàng)目（20124321120006）（Project （201304504） supported by the National Forestry Science Research； Projects （51178175， 51204215） supported by the National Natural Science Foundation of China； Project （13JJ5027） supported by the Natural Science Foundation of Hunan Province； Project （20124321120006） supported by Research Fund for the Doctoral Program of Higher Education of China）

周先雁，教授，從事工程抗震研究；E-mail：yinjiang2013@outlook.com