磁流體對雙噴嘴擋板伺服閥工作性能的影響

胡均平，李科軍(中南大學 機電工程學院，湖南 長沙，410083)

磁流體對雙噴嘴擋板伺服閥工作性能的影響

胡均平，李科軍
(中南大學 機電工程學院，湖南 長沙，410083)

通過分析伺服閥的工作原理及力矩馬達工作間隙中磁流體的作用機理，運用鍵合圖理論以規范的方式統一描述系統中的機液能量耦合、流體磁化以及電磁轉換等多種能量作用；考慮磁流體作用力等非線性因素，采用集中參數建立電液伺服閥的通用仿真數學模型，模擬添加磁流體前后及力矩馬達工作氣隙參數變化對伺服閥工作性能的影響規律，通過試驗證明該模型的有效性。研究結果表明：添加磁流體可增加伺服閥力矩馬達的阻尼比，提高系統的穩定性和抗干擾能力；增大工作氣隙高度或減小導磁體有效工作面積均有利于提高系統的穩定性，但降低了系統的流量增益。

磁流體；雙噴嘴擋板伺服閥；鍵合圖；仿真

雙噴嘴擋板伺服閥具有結構緊湊、線性度好和動態響應速度快等優點，廣泛應用于工程機械、自動生產流水線和航空航天等工業設備中[1]。作為液壓系統的核心元件，雙噴嘴擋板伺服閥直接影響著系統工作特性參數，因而人們對其進行了較多研究，如：集中于電液伺服系統控制穩定性和快速性的研究[2-4]，針對力矩馬達電磁回路[5]、力矩馬達諧響應及力反饋彈簧組件強度[6]等伺服閥的結構特性分析，伺服閥新結構、新材料的應用[7-8]。此外，對伺服閥的故障診斷[9-10]、測試方法[11]及測試誤差[12]等也進行了研究。

1　雙噴嘴擋板伺服閥結構原理

圖1所示為雙噴嘴擋板伺服閥的結構原理圖。主要由電氣-機械轉換裝置、液壓放大器平衡2部分組成。電氣-機械轉換裝置可以將輸入的電信號轉化成力矩馬達的轉角輸出。液壓放大器將輸入主滑滑閥11的位移轉化成負載壓力和負載流量。反饋平衡機構主要由阻尼孔、噴嘴和擋板8、反饋桿9組成，是聯系電氣-機械轉換裝置和液壓放大器的樞紐，將銜鐵的轉角轉化為滑閥的位移輸出。當電磁線圈有電流i輸入時，通過電樞的永久磁鐵產生1個力，這個力連接到彈簧管7上產生1個順時針方向的力矩。與彈簧管連接的擋板8離開中間位置改變了噴嘴左右間隙形成1個壓力差，作用在主閥閥芯11上，推動其向右運動，由此A口接壓力油，B口接回油。同時，主閥閥芯11通過反饋桿9連接到噴嘴擋板和力矩馬達上，隨著閥芯位置改變，反饋桿和彈簧管的反饋扭矩和力矩馬達的電磁扭矩達到平衡，閥芯的行程和先導控制閥的流量實現閉環控制，與輸入電流信號成正比。當輸入電流反向時，力矩馬達逆時針偏轉，主閥芯向左運動直至平衡，由此B口接壓力油，A口接回油，具體運動過程與電流正向時的類似。

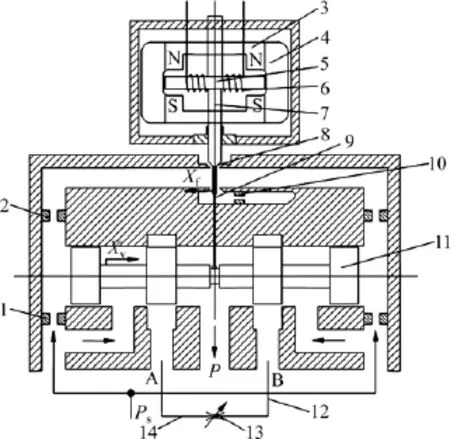
圖1　雙噴嘴擋板伺服閥結構Fig.1　Schematic diagram of twin flapper-nozzle servo-valve

2　雙噴嘴擋板伺服閥建模

通過分析雙噴嘴擋板電液伺服閥的結構特點與工作原理，將雙噴嘴擋板電液伺服閥分為電磁先導子系統(第1級子系統)和液壓放大子系統(第2級子系統)。電磁先導子系統包括彈簧管、銜鐵、擋板和電磁線圈等；液壓放大子系統包括壓力源、主閥閥芯和反饋桿等。在對伺服閥建模前需進行以下簡化：1)伺服閥阻尼孔的液阻、工作容腔的液容和主閥閥芯質量等采用集中參數法處理；2)液壓源油液的壓力、溫度恒定，回油口壓力為零；3)在主閥閥芯開啟的運動過程中忽略瞬態液動力，只考慮穩態液動力；4)磁流體始終保持在力矩馬達的工作間隙中。

2.1第1級子系統建模

2.1.1銜鐵和擋板組件運動的數學模型

銜鐵和擋板組件運動關系如圖2所示。

當電磁線圈輸入電流i時，銜鐵在電磁力矩作用下順時針偏轉，銜鐵、擋板組件具有2個自由度：一個是銜鐵的轉動速度a.，另一個是組件重心沿x軸方向的運動速度 gx.。當參數a.和 gx.已知時，可以根據組件工作點的幾何尺寸關系，計算各點的對應速度：

圖2　銜鐵和擋板組件運動關系Fig.2　Motion relation diagram of armature and baffle component

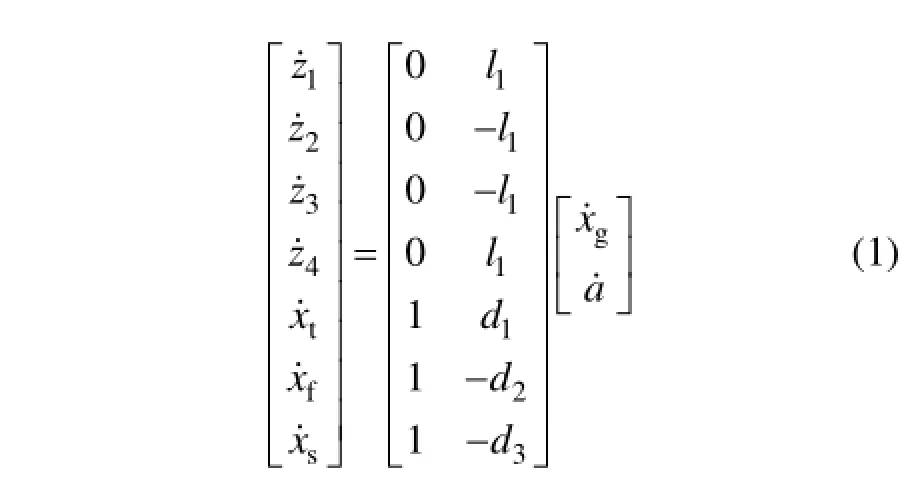
2.1.2添加磁流體的力矩馬達的數學模型

添加磁流體的力矩馬達結構如圖3所示。磁流體對力矩馬達銜鐵的作用力可分為彈性阻力Ft和黏性阻力Fn，可分別表示如下：

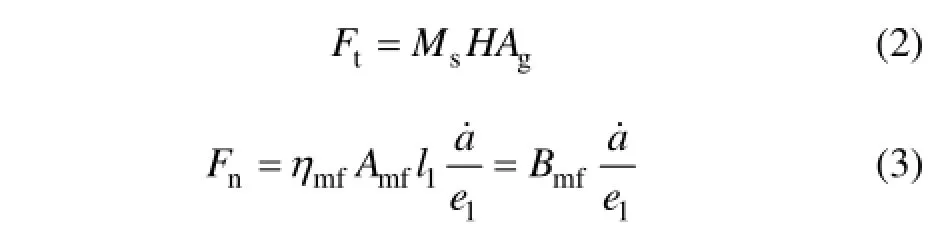
圖3　添加磁流體的力矩馬達Fig.3　Scheme for torque motor adding magnetic fluid

式中：Ft為銜鐵表面的彈性阻力；Ms為磁流體的飽和磁化強度；H為工作間隙中的磁場強度；Ag為垂直銜鐵運動方向磁流體與銜鐵的有效接觸面積；mfη為磁流體黏度，與磁場強度有關，為簡化計算，近似取常數；Amf為沿銜鐵運動方向磁流體與銜鐵的有效接觸面積；e1為磁流體厚度，近似為工作氣隙高度。

力矩馬達工作磁路的等效原理如圖4所示，可以看出：處于對角臂的磁通是相等的。以分別包含2對角橋臂的2個電磁回路為分析對象，當銜鐵位置變化時，磁阻R1和R2分別為：

式中：e2和R0分別為銜鐵在中間工作位置時的氣隙長度和電磁磁阻；S為導磁體通過氣隙的工作面積；μ0為導磁率；z1和z2處于對角橋臂位置，因此有z2=-z1。

通過磁阻R1和R2的磁通分別為：

式中：E0為電磁鐵的磁動勢；N為每個線圈的匝數。銜鐵產生的的轉動力矩為

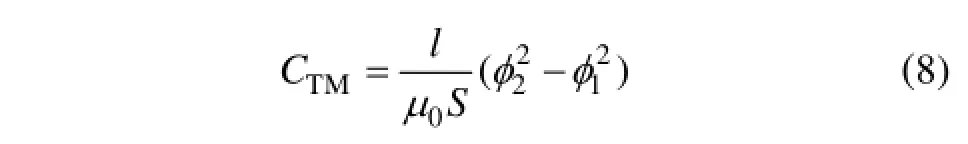
將式(6)和(7)代入式(8)得

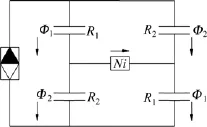
圖4　力矩馬達的磁路原理圖Fig.4　Principle diagram of magnetic circuit of torque motor

式(9)經線性化處理得[1]

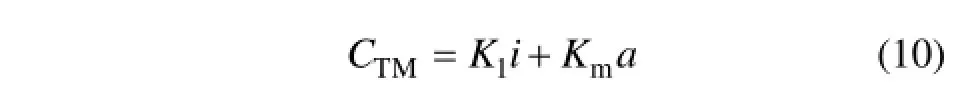
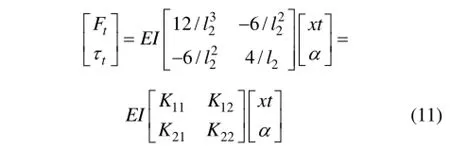
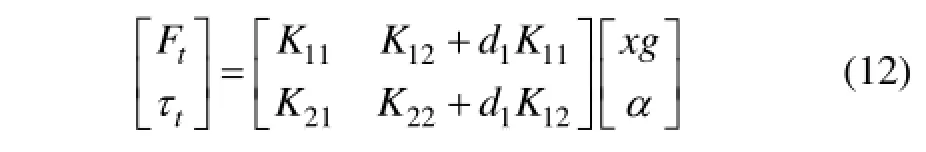
可用二通口C場鍵元表示彈簧管施加的力矩和力。聯合式(4)~(7)，工作氣隙的磁場強度H1和H2可表示為：

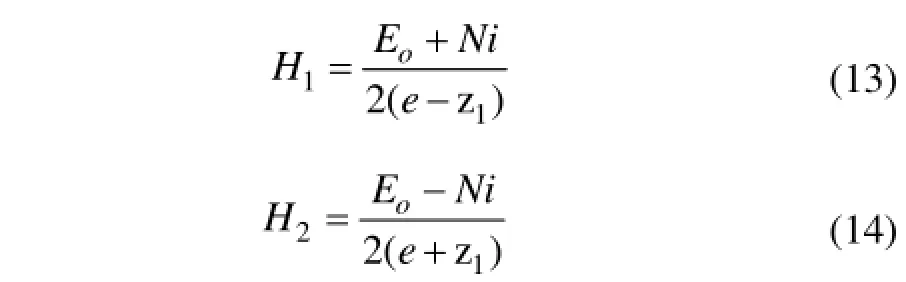
聯合式(2)，(3)，(13)和(14)可得磁流體產生的負載力矩為

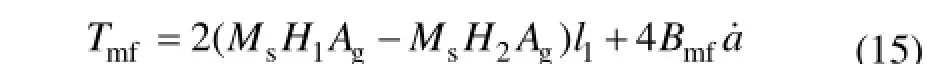
2.1.3第1級子系統鍵合圖模型

應用鍵合圖建模規則，結合式(1)，(10)，(12)和(15)，建立第1級子系統的鍵合圖模型，如圖5所示。圖5中：輸入電流i通過表示電磁線圈匝數的回轉器GY結轉化為磁動勢，再結合電磁鐵磁動勢E0和對角橋臂磁阻R1和R2，經銜鐵輸出電磁轉矩CTM，同時有磁流體對銜鐵的轉矩作用Tmf，再經彈簧管和反饋桿傳遞到主閥閥芯。1結上的變量和分別表示銜鐵、擋板組件水平方向和轉動方向的速度；Ma，Ja，Rt和Ra分別為銜鐵與擋板組件的質量、等效轉動慣量、運動阻尼系數和轉動阻尼系數；1結上的變量和分別表示反饋桿作用主閥閥芯處圓球和噴嘴處擋板的運動速度；Kw為反饋桿的等效剛度系數；為主閥閥芯沿x軸方向的速度。

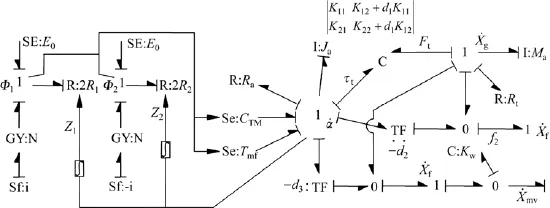
圖5　第1級子系統鍵合圖模型Fig.5　Bond graph model of the first level subsystem

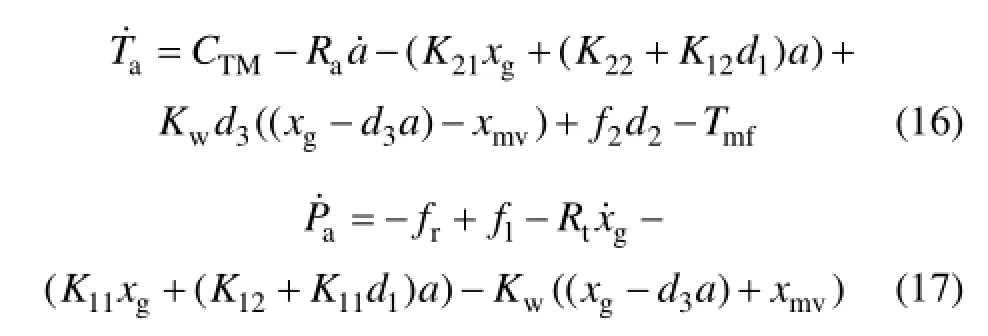
2.2第2級子系統建模

圖6所示為伺服閥液壓放大子系統的工作過程。根據系統的功率流向和鍵合圖建模方法，建立圖7所示的鍵合圖模型。圖7中：Amv，Rmv和Fmv分別為主閥閥芯的有效作用面積、穩態液動力和運動阻尼系數；Ps為液壓源壓力；Rlmv1，Rlmv2，Rrmv1和Rrmv2為閥套與主閥閥芯之間的泄漏液阻，流過的流量分別為，和；miR和moR為伺服閥進出口的液阻，流過的流量分別為和；Rlfr1，Rlfr2，Rrfr1，Rrfr2和Rod為液壓源流經固定阻尼孔到噴嘴控制口的等效液阻，流過的流量分別為和；Afl為噴嘴處擋板兩端油液作用面積；Rlfn和Rrfn分別為噴嘴處左右兩邊的等效液阻，由噴嘴處擋板位移 xf控制，流過的流量分別為和；Kl1，Kl2，Kr1，Kr2，Kd，Kp1和Kp2分別為圖6中對應各工作容腔的等效液壓剛度；Rld為伺服閥外接節流閥的液阻，流過的流量為ldV.。

各個容腔的流量變化為：

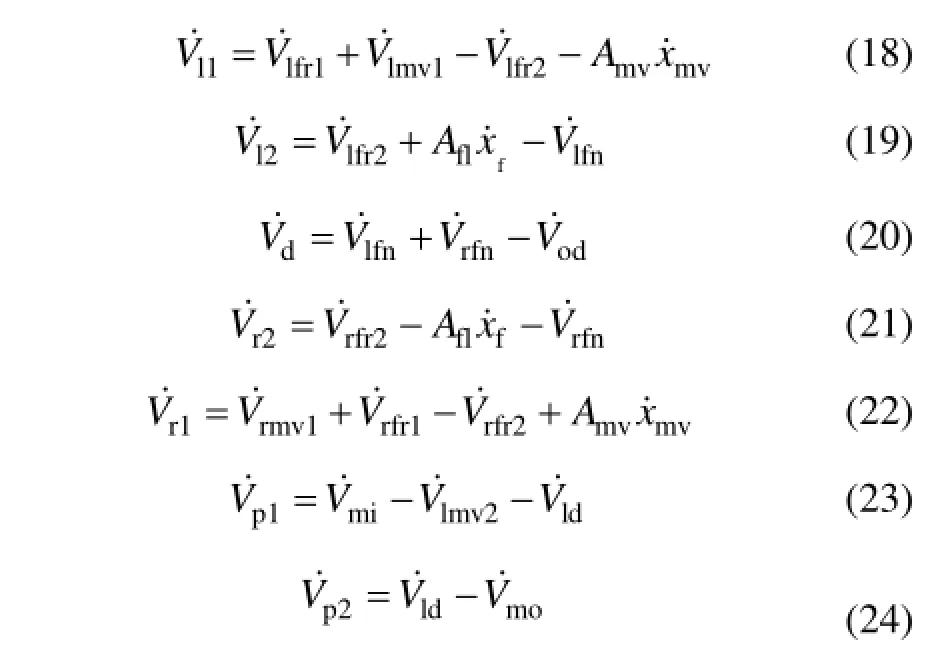
主閥閥芯的動力學平衡方程為

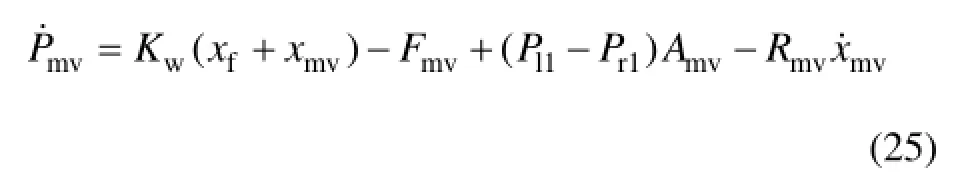
噴嘴處擋板的動力學平衡方程為

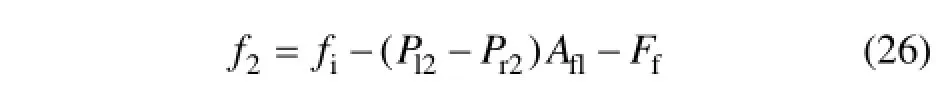
式中：Ff為油液作用在擋板上的液動力；fi為擋板在噴嘴處產生的彈性接觸力；只有當時才會出現，其余時間該計算項為0 N。液動力Ff和接觸力fi[1]可分別用下式表示：

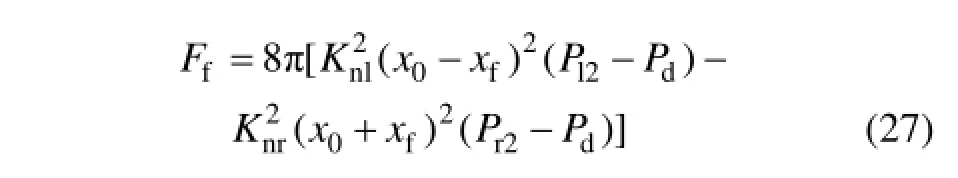
當|xf|-x0＞0時，

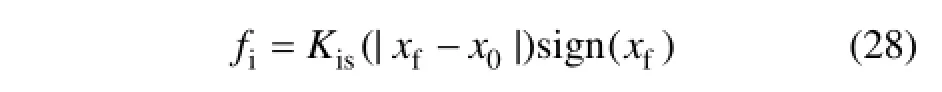
圖6　第2級子系統結構簡圖Fig.6　Structure diagram of the second subsystem

式中：Kis為沖擊剛度系數；xf為噴嘴處擋板移動的距離；x0為擋板處于中心位置時擋板噴嘴的距離。各個容腔的壓力可分別表示為：；；；；；；。式中各參數含義見圖6和圖7。

圖7　第2級子系統鍵合圖模型Fig.7　Bond graph model of the second subsystem

2.3雙噴嘴擋板伺服閥鍵合圖模型

根據伺服閥工作的功率流向及主閥閥芯和反饋桿的位移協調關系，將以上2個子系統進行集成拼裝，建立雙噴嘴擋板伺服閥的鍵合圖模型，如圖8所示。其中，噴嘴擋板、節流孔、閥口等處的液阻都是導納型因果關系，而且噴嘴擋板、閥口處的液阻與開口面積有關。

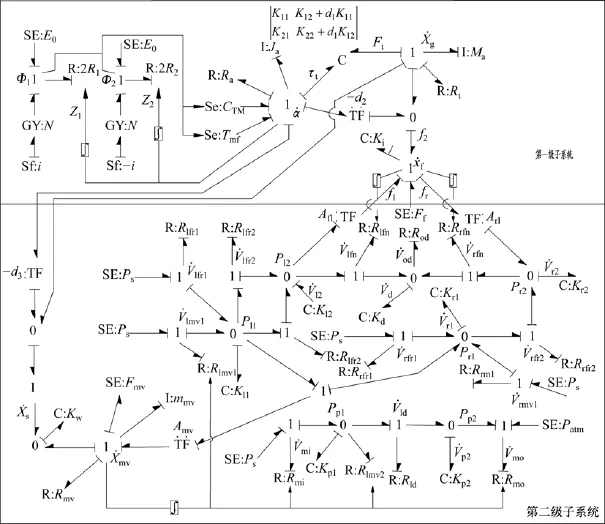
圖8　雙噴嘴擋板伺服閥鍵合圖模型Fig.8　Bond graph model of twin flapper-nozzle servo valve

3　仿真分析

基于以上建立的數學模型，采用Matlab對伺服閥工作過程進行數值模擬，運用四階龍格-庫塔法運算程序進行計算。主要仿真參數見表1，仿真時間設為80 ms。

3.1磁流體對伺服閥工作性能影響

對雙噴嘴擋板伺服閥添加磁流體與不添加磁流體2種情況的動態特性進行分析，得到主閥閥芯位移、系統輸出流量和銜鐵轉角在階躍輸入電流下的響應特性，如圖9所示。分析圖9可知：

1)添加磁流體后，系統響應延遲，系統峰值時間增加約1.5 ms，但振蕩次數減少，振蕩幅值減小。如銜鐵轉角響應曲線在第2次振蕩時，其幅值減小24%左右，最終系統的調節時間提前約6 ms。這說明磁流體的特殊性質增加了銜鐵運動的彈性阻力和黏性阻力，導致力矩馬達的響應時間增加，但又因磁流體的阻尼作用，增強了系統的抗干擾能力，提高了系統的穩定性。

2)當系統穩定時，添加磁流體與未添加磁流體時的各狀態變量穩態值基本相等。這是因為磁流體對銜鐵的作用等效于機械彈簧，其作用力與力矩馬達工作間隙、銜鐵轉角、輸入電流相關，但當作用在擋板上的諸作用力矩達到平衡、銜鐵回復到中位時，磁流體的阻尼作用基本消失，而主閥閥芯位置主要由力矩馬達輸出扭矩決定，因此，主閥閥芯位移及系統輸出流量等基本相同。

3.2工作氣隙高度對伺服閥工作性能影響

添加磁流體后，其他值不變，改變力矩馬達的工作氣隙高度，分別取值為0.295,0.310和0.325 mm。不同工作氣隙高度下的主閥閥芯位移、系統輸出流量和銜鐵轉角的階躍響應變化如圖10所示。從圖10可以看出：

1)隨著工作氣隙高度的增加，系統振蕩的峰值減小，振蕩次數減少，最終穩定過程比較平緩，即系統趨于穩定的時間較短；當工作氣隙的高度由0.295 mm增至0.325 mm時，系統調節時間由75 ms減至40 ms。這是因為受迫振動的振幅和激振力成正比，當減小激振力(力矩馬達的輸出力矩隨工作氣隙高度增大而減小)時，系統的振蕩幅度隨之減小，加之磁流體的阻尼作用，提高了系統的穩定性。

表1　伺服閥仿真參數Table 1　Simulation parameters for servo-valve

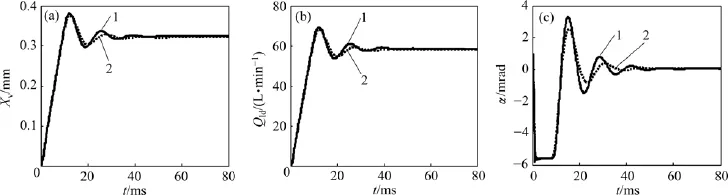
圖9　磁流體對伺服工作性能的影響Fig.9　Effect of magnetic fluids on working performance of servo value

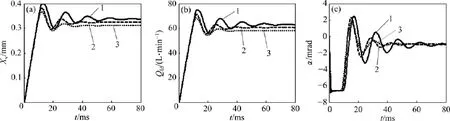
圖10　工作氣隙高度對伺服閥工作性能的影響Fig.10　Effect of working air gap height on working performance of servo value

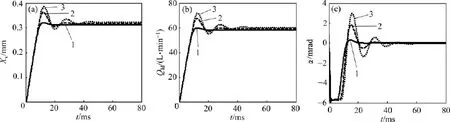
圖11　導磁體工作面積對伺服閥工作性能的影響Fig.11　Effect of magnetizer working area on working performance of servo value

2)當工作氣隙高度由0.295 mm增至0.325 mm時，主閥閥芯位移的穩態值由 0.340 mm減小至0.312 mm，系統輸出流量的穩態值由63 L/min減小至58 L/min。這是因為力矩馬達的輸出力矩隨著工作氣隙高度增大而減小，使得銜鐵回復中位時，主閥閥芯位移及系統輸出流量減小。

3.3導磁體工作面積對伺服閥工作性能影響

添加磁流體后，其他值不變。圖11所示為工作氣隙處導磁體的工作面積分別為14.9，15.1和15.3 mm2時，經仿真分析得到主閥閥芯位移、系統輸出流量和銜鐵轉角的階躍響應變化，通過分析可得：

1)隨著導磁體工作面積的增大，系統的動態響應加快，振蕩幅值增大，振蕩次數增加，趨于穩定的持續時間增加；當工作面積由14.9 mm2增至15.3 mm2時，系統的調節時間由10 ms增至40 ms，可見系統的穩定性明顯變差。

2)當工作面積由14.9 mm2增至15.3 mm2時，主閥閥芯位移的穩態值由0.33 mm增至0.35 mm，系統輸出流量的穩態值由58 L/min增至63 L/min。這是因為力矩馬達的輸出扭矩與導磁體的工作面積成正比，當工作面增大時，主閥閥芯位移與系統輸出流量隨之增大。銜鐵最終回復中位，銜鐵轉角為0°。

4　試驗分析

為驗證模型的合理性和準確性，對雙噴嘴擋板伺服閥進行負載流量階躍響應實驗，實驗結果如圖12所示。從圖12可以看出，與試驗結果相比，試驗曲線的峰值時間為14 ms，增加2 ms左右。經過一定時間振蕩后，兩者達到穩定狀態的調節時間基本一致，都是32 ms左右，但試驗穩態流量值減小1.5 L/min。導致此差異的原因是多方面的，如試驗過程中傳感器測量誤差、計算過程中壓力源壓力保持恒定和元件參數取值誤差等，這些都對計算結果造成了實際影響。但通過對比分析整條曲線的仿真結果具有一定精度，證明了所建伺服閥鍵合圖模型的準確性。

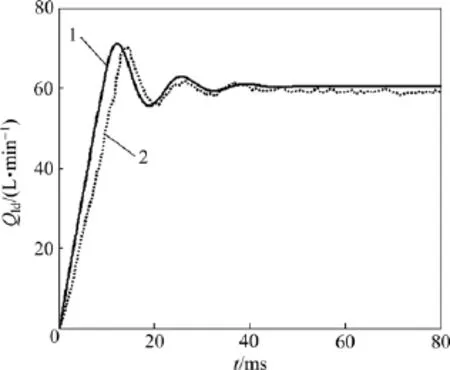
圖12　階躍輸入電流信號的流量響應Fig.12　Flow responses of input step current signal

5　結論

1)添加磁流體后，系統的振蕩峰值和幅度均減小，振蕩次數減少，調節時間提前，可見磁流體的阻尼作用提高了系統的穩定性，但增加了系統的響應時間。系統平衡時，各狀態變量穩態值基本不變。

2)減小工作氣隙的高度即減小了力矩馬達的輸出扭矩，可以提高系統的穩定性，但系統輸出流量也隨之減小；而增大工作氣隙的高度，容易造成系統產生高頻振蕩，系統沖擊較大，穩定性差。設計時應權衡考慮。

3)增大導磁體有效工作面積，提高了系統的輸出流量，但系統穩定性變差。可通過選用具有更高黏性阻尼和彈性系數的磁流體來保證系統良好的動態穩定性，但同時應兼顧系統的響應時間。

[1]李壯云.液壓元件與系統[M].北京:機械工業出版社,2011: 255-275. LI Zhuangyun.Hydraulic components and system[M].Beijing: China Machine Press,2011:255-275.

[2]王勇勤,張云飛,嚴興春,等.伺服閥非線性特性建模的液壓彎輥系統動態特性[J].重慶大學學報(自然科學版),2005,28 (11):5-7. WANG Yongqin,ZHANG Yunfei,YAN Xingchun,et al. Nonlinear characteristic modeling of servo valve on hydraulic bending roll system’s dynamic characteristic[J].Journal of Chongqing University(Natural Science Edition),2005,28(11): 5-7.

[3]孫萌,李長春,延皓,等.閥控非對稱缸位置系統的非線性建模[J].北京交通大學學報,2012,36(4):164-168. SUN Meng,LI Changchun,YAN Hao,et al.Nonlinear modeling for valve controlled asymmetric cylinder position system[J]. Journal of Beijing Jiaotong University,2012,36(4):164-168.

[4]江桂云，王勇勤，嚴興春.液壓伺服閥控缸動態特性數學建模及仿真分析[J].四川大學學報(工程科學版),2008,40(5): 690-693. JIANG Guiyun,WANG Yongqing,YAN Xinchun.Mathematics modeling and simulation analysis of dynamic characteristics for hydraulic cylinder controlled by servo valve[J].Journal of Sichuan University(Engineering Science Edition),2008,40(5): 690-693.

[5]URATA E.Study of magnetic circuits for servo-valve torque motors[C]//Bath Workshop on Power Transmission and Control (PTMC).Bath,UK,2000:269-282.

[6]彭敬輝,李松晶,JACOB M M.電磁力與射流流場中壓力脈動作用下伺服閥力矩馬達諧響應分析[J].工程力學,2012, 30(2):348-353. PENG Jinghui,LI Songjing,JACOB M M.Harmonic response analysis of a hydraulic servo-valve torque motor under the action of electromagnetic force and pressure fluctuation in jet flow field[J].Engineering Mechanics,2012,30(2):348-353.

[7]曲興田,鄂世舉,吳博達,等.雙壓電晶片驅動噴嘴擋板式伺服閥[J].吉林大學學報(工學版),2005,35(2):153-156. QU Xingtian,E Shiju,WU Boda,et al.Nozzle flapper servo valve driven by piezoelectric bimorph[J].Journal of Jilin University(Engineering Science),2005,35(2):153-156.

[8]周淼磊,楊志剛,高巍,等.高速精密壓電型電液伺服閥及其控制方法[J].哈爾濱工業大學學報,2009,41(9):160-163. ZHOU Miaolei,YANG Zhigang,GAO Wei,et al.High-speed and precise piezoelectric electro-hydraulic servo valve and its control method[J].Journal of Harbin Institute of Technology, 2009,41(9):160-163.

[9]馮偉,凌英,張文,等.發電機組電液伺服閥失效分析[J].潤滑與密封,2014,39(3):120-124. FENG Wei,LING Ying,ZHANG Wen,et al.Failure analysis of electro-hydraulic servo valve for generator unit[J].Lubrication Engineering,2014,39(3):120-124.

[10]赫圣橋,許黎明,沈偉,等.電液伺服閥狀態在線特征提取和異常檢測方法[J].上海交通大學學報,2010,44(12): 1747-1752. HAO Shengqiao,XU Liming,SHEN Wei,et al.On-line fault feature extraction and abnormality detection of electro-hydraulic servovalve’scondition[J].JournalofShanghaiJiaotong University,2010,44(12):1747-1752.

[11] 汪首坤,王軍政,李金倉.基于位移測量的電液伺服閥動態測試方法[J].北京理工大學學報,2011,31(6):666-669. WANG Shoukun,WANG Junzheng,LI Jincang.A new testing method for dynamic performance of servo valves based on displacement measurement[J].Transactions of Beijing Institute of Technology,2011,31(6):666-669.

[12]李健鋒,吳張永.電液伺服閥測試誤差分析[J].液壓氣動與密封,2013(5):51-56. LI Jianfeng,WU Zhangyong.Test error analysis of electro hydraulic servo valve[J].Hydraulics Pneumatics&Seals, 2013(5):51-56.

[13]李松晶,鮑文.磁流體對伺服閥力矩馬達動態特性的影響[J].機械工程學報,2008,44(12):137-142. LI Songjing,BAO Wen.Influence on dynamic characteristics of a hydraulic servo-valve torque motor due to magnetic fluids[J]. Chinese Journal of Mechanical Engineering,2008,44(12): 137-142.

[14]KRAKOV M S.Influence of rheological properties of magnetic fluid on damping ability of magnetic fluid shock-absorber[J]. Journal of Magnetism and Magnetic Materials,1999,201(7): 368-371.

[15]KARNOPP D C,MARGOLIS D L,ROSENBERG R C.System dynamics:modeling,simulation,and control of mechatronic systems[M].New York:John Wiley&Sons,2012:13-36.

[16]BORUTZKY W.Bond graph methodology:development and analysisofmultidisciplinarydynamicsystemmodels[M]. London:Springer Verlag,2009:89-128.

(編輯陳燦華)

Influence of magnetic fluids on working performance of twin flapper-nozzle servo valve

HU Junping,LI Kejun
(School of Mechanical and Electrical Engineering,Central South University,Changsha 410083,China)

By analyzing the working principle of servo valve and the mechanism of the magnetic fluids filled into the working gaps of a torque motor,the bond graph method was introduced to describe the energy input,transfer,translation and dissipation of the system,and the lump parameters model of the system was developed in a unified way,in which the magnetic resistance and other nonlinear factors were taken into consideration.The system state equations were derived from the model.The effects of magnetic fluids and the working air gap parameters on the dynamic characteristics of servo-valve were studied by numerical simulation,and the model was verified experimentally.The results show that the magnetic fluid can be used to increase the torque motor damping ratio to improve the system stability.Increasing the height of air gap and reducing the working area of magnetizer can improve the system’s stability,but reduce the flow gain of the system.

magnetic fluids;twin flapper-nozzle servo valve;bond graph;simulation

李科軍，博士研究生，從事工程機械液壓系統設計與仿真研究；E-mail:likejuncsu@126.com隨著液壓伺服系統向高速高精高效方向的發展，要求雙噴嘴擋板伺服閥工作性能更加穩定。為克服噴嘴與擋板之間的流場產生的氣穴和剪切層振蕩，提高伺服閥的抗干擾能力，李松晶等[13]利用磁流體在外加磁場作用下具有較高飽和磁化強度和較大黏度的工作特性[14]，將其添加到伺服閥力矩馬達的工作氣隙中，改善了伺服閥力矩馬達的穩定性。但在建模過程中忽略了力矩馬達和液壓部分的相互作用，影響了結果的精度，而且無法深入考察伺服閥內部狀態的變化過程。因此，有必要建立伺服閥的全局耦合動力學模型。雙噴嘴擋板伺服閥工作時是一個多能域耦合的復雜非線性系統，單獨對電磁系統[5]、反饋機構或液壓系統[3-4]的分析無法實現系統整體性能最優；而且對于多能域耦合的復雜非線性系統，傳統的建模方法相當繁瑣，且往往難以實現，甚至無效。鍵合圖法(為該問題的解決提供了頗具特色的途徑)[15-16]可以直接基于物理描述對多域系統使用相同的符號進行可視化建模，并借助計算機實現系統的自動鍵合圖建模和動態特性分析。為此，本文作者從雙噴嘴擋板伺服閥具體工作機理出發，根據伺服閥的結構特點和功率流分布形式，采用功率鍵合圖法，準確地構建添加磁流體后雙噴嘴擋板伺服閥的仿真模型。

TH137.52；TB34

A

1672-7207(2016)07-2287-09

10.11817/j.issn.1672-7207.2016.07.016

2015-08-10；

2015-10-22

國家自然科學基金資助項目(51175518)(Project(51175518)supported by the National Natural Science Foundation of China)