卷積定理與傅里葉變換性質及其應用的關系探討

黃金平,張正炳

(長江大學電子信息學院，湖北 荊州 434023)

?

卷積定理與傅里葉變換性質及其應用的關系探討

黃金平,張正炳

(長江大學電子信息學院，湖北 荊州 434023)

為解決學生學習傅里葉變換這部分內容感覺困難的問題，深入研究了傅里葉變換性質之間的內在聯系。傅里葉變換的時移性質、時域微分性質、時域積分性質、頻移性質、頻域微分性質等許多性質只是時域卷積定理和頻域卷積定理的特例，而傅里葉變換的獨立性質只有線性性質、尺度性質、對偶性質和卷積定理。這一發現對傅里葉變換一章的教學具有重要參考價值，結合傅里葉變換性質內在聯系的新教學方案將使得學生學習傅里葉變換的內容不僅易于理解，而且條理清晰，便于記憶，從而解決“傅里葉變換難”的問題。

卷積定理；傅里葉變換；性質；應用

在教學與教研活動中，筆者發現傅里葉變換的性質并非如現存各版本的《信號與系統》[1,2]教材上所編寫的看似彼此孤立，而是有著嚴密數學聯系的統一、有機整體。在傅里葉變換的眾多性質中，卷積定理有著特別的作用：透過卷積定理不僅能揭示這些性質之間的相互關系，而且可以推導出傅里葉變換在電子技術中的諸多重要應用。為此，筆者試著從卷積定理出發，探討卷積定理與傅里葉變換性質以及傅里葉變換的幾個典型應用之間的關系。

1　卷積定理

卷積定理包括時域卷積定理和頻域卷積定理。

定理1(時域卷積定理)若f1(t)?F1(jω)，f2(t)?F1(jω)，則f1(t)與f2(t)的卷積f1(t)*f2(t)的傅里葉變換為F1(jω)F2(jω)。

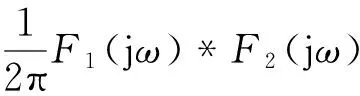
關于這2個定理，可以利用卷積的定義和傅里葉變換的定義[3]很容易得到證明。

2　時域卷積定理與傅里葉變換性質及應用的關系

2.1時域卷積定理與時移性質

在時域中，設f1(t)=f(t)，f2(t)=δ(t-t0)，由于f1(t)*f2(t)=f(t)*δ(t-t0)=f(t-t0)，即時移。

在頻域中，設f1(t)=f(t)?F(jω)，由于f2(t)=δ(t-t0) ?ejωt0，據時域卷積定理得：

f(t-t0)?F1(jω)F2(jω)=F(jω)ejωt0

(1)

式(1)就是傅里葉變換的時移性質。

2.2時域卷積定理與微分性質

在時域中，設f1(t)=f(t)，f2(t)=δ′(t)，由于f1(t)*f2(t)=f(t)*δ′(t)=f′(t)，即時域微分。

在頻域中，設f1(t)=f(t)?F(jω)，由于f2(t)=δ′(t)?(jω)，據時域卷積定理得：

f′(t)?F1(jω)F2(jω)=jωF(jω)

(2)

式(2)就是傅里葉變換的時域微分性質。

2.3時域卷積定理與積分性質

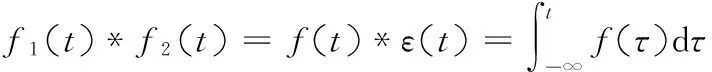
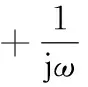
(3)

式(3)就是傅里葉變換的時域積分性質。

2.4時域卷積定理與系統函數

在時域中，設f1(t)=δ(t)，f2(t)=h(t)，由于f1(t)*f2(t)=δ(t)*h(t)=h(t)，即系統沖激響應。

在頻域中，由于f1(t)=δ(t)?1，由于f2(t)=h(t)?H(jω)，據時域卷積定理得：

h(t)?F1(jω)F2(jω)=H(jω)

(4)

式(4)就是系統函數[4]。

2.5時域卷積定理與系統的零狀態響應

在時域中，設f1(t)=f(t)，f2(t)=h(t)，由于f1(t)*f2(t)=f(t)*h(t)=yzs(t)，即系統零狀態響應。

在頻域中，設f1(t)=f(t)?F(jω)，f2(t)=h(t)?H(jω)，據時域卷積定理得：

yzs(t)=h(t)*f(t)?F1(jω)F2(jω)=H(jω)F(jω)

(5)

式(5)就是零狀態響應的頻域分析法[5]。

2.6時域卷積定理與系統的無失真傳輸條件

在時域中，設f1(t)=f(t)，f2(t)=Kδ(t-t0)，由于f1(t)*f2(t)=f(t)*Kδ(t-t0)=Kf(t-t0)，即系統無失真傳輸。

在頻域中，設f1(t)=f(t)?f(jω)，f2(t)=Kδ(t-t0)?Kejωt0，據時域卷積定理得：

Kf(t-t0)=Kδ(t-t0)*f(t)?F1(jω)F2(jω)=KF(jω)ejωt0

(6)

式(6)就是系統的無失真傳輸條件。

2.7時域卷積定理與正弦穩態響應

在時域中，設f1(t)=ejω0t，f2(t)=h(t)，由于f1(t)*f2(t)=ejω0t*h(t)=H(jω)ejω0t，即系統正弦穩態響應。

在頻域中，設f1(t)=ejω0t?2πδ(ω-ω0)，f2(t)=h(t)?H(jω)，據時域卷積定理得：

yss(t)=h(t)*f(t)=H(jω)ejω0t?F1(jω)F2(jω)=2πδ(ω-ω0)H(jω)

=2πH(jω0)δ(ω-ω0)

(7)

式(7)就是系統正弦穩態響應的頻域分析法[5]。

由以上分析可見，根據傅里葉變換的時域卷積定理可推導出如式(1)～(7)所示的傅里葉變換的時移性質、微分性質、積分性質，并能得出系統函數與系統沖激響應的關系、系統零狀態響應的求法、解釋系統無失真傳輸條件、系統正弦穩態響應的求法等。這些性質實際上只是時域卷積定理的特例，總結歸納于表1中。

3　頻域卷積定理與傅里葉變換性質及應用的關系

3.1頻域卷積定理與頻移性質

在時域中，設f1(t)=f(t)，f2(t)=e±jω0t，則f1(t)f2(t)=f(t)e±jω0t。

在頻域中，設f1(t)=f(t)?F(jω)，由于f2(t)=e±jω0t?2πδ(ω?ω0) ，據頻域卷積定理得：

(8)

式(8)就是傅里葉變換的頻移性質。

表1　時域卷積定理與傅里葉變換其他性質關系和幾個典型應用

3.2頻域卷積定理與頻域微分性質

在時域中，設f1(t)=f(t)，f2(t)=-jt，則f1(t)f2(t)=-jtf(t)。

在頻域中，設f1(t)=f(t)?F(jω)，由于f2(t)=-jt?2πδ′(ω)，據頻域卷積定理得：

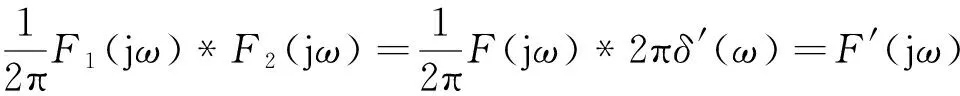
(9)

式(9)就是傅里葉變換的頻域微分性質。

3.3頻域卷積定理與調制

在時域中，設f1(t)=f(t)，f2(t)=cosω0t，則f1(t)f2(t)=f(t)cosω0t，即振幅調制。

在頻域中，設f1(t)=f(t)?F(jω)，由于f2(t)=cosω0t?π[δ(ω-ω0)+δ(ω+ω0)]，據頻域卷積定理得：

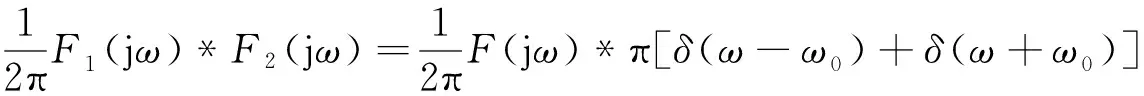
(10)

式(10)就是振幅調制定理[3]。

由以上分析可見，據傅里葉變換的頻域卷積定理可推導出如式(8)～(10)所示的傅里葉變換的頻移性質、頻域微分性質，并能得出指導通信實踐的振幅調制定理。這些性質歸納于表2。

4　結語

在多年的教學實踐和長江大學省級精品資源共享課程《信號與系統分析》的建設實踐中，為解決學生對傅里葉變換這一章內容學習困難的問題，筆者所在教學團隊積極開展研究和探索，結合傅里葉變換性質之間的內在聯系，摸索出了一套的新的講授方案，具體講授次序依次為：先提出傅里葉變換的定義，

[1]奧本海姆 (美).信號與系統[M].第3版.劉樹棠譯.北京：電子工業出版社，2013.

[2] 鄭君里.信號與系統[M].第3版.北京：高等教育出版社，2014.

[3] 金波,張正炳.信號與系統分析[M].北京：高等教育出版社，2011.

[4] 管致中,夏恭恪,孟橋.信號與線性系統[M].第5版.北京：高等教育出版社，2014.

[5] 張小虹.信號與系統[M].第2版.陜西：西安電子電子科技大學出版社，2012.

[6] 沈元隆,周井泉.信號與系統[M].北京：人民郵電出版社，2007.

[編輯]洪云飛

2016-04-23

湖北高校省級精品資源共享課程。

黃金平(1965-),男,副教授,現主要從事電子與信息方面的教學與研究工作；E-mail:1103934907@qq.com。

O441

A

1673-1409(2016)19-0029-03

[引著格式]黃金平,張正炳.卷積定理與傅里葉變換性質及其應用的關系探討[J].長江大學學報(自科版)，2016,13(19)：29～31，41.