“對數函數”教學中必須厘清的幾個問題

廣東省東莞市教研室　(523000)

易文輝

?

“對數函數”教學中必須厘清的幾個問題

廣東省東莞市教研室(523000)

易文輝

“對數函數”是高中數學函數內容的重點之一，是高中數學以“函數”與“運算”為主線的直接體現，是解決實際問題的一個重要函數模型，有非常廣泛的實際應用背景；對數運算及對數函數的相關問題也是聯系初等數學和高等數學的一個重要紐帶，在歷年的高考試題中，以對數函數為命題背景，結合高數知識、初等數學的最新研究成果的探究性試題在全國各地高考試卷中累見不鮮.

“對數函數”的內容在人教A版教材必修1第二章第2節，是高一學生學習的難點之一，對于對數的概念、運算及其圖像性質即使到了高三，許多同學依然難于理解，其根源在高一學習時就遺留了許多問題，“對數函數”的學習是培養高一學生學習數學興趣及其思維能力的一個重要載體，其教學的質量也是教師專業素養的直接體現，筆者認為要提高“對數函數”的教學效果，必須要厘清幾個問題.

1　厘清“對數”的來源

1.1讓概念的引入更加合理和自然

數學課堂應該對本原性問題多一些思考，圍繞它來確立數學探究活動[1]，這里的本原性問題是指符合學生認知特點、科學的、能夠體現知識的來源即本質的問題，主要有實際問題和數學內部的問題.而在教材中對數和對數函數的概念引入中，背景問題與知識概念產生沒有“必要”聯系，有些牽強(許多人稱之為偽問題)，概念的給出也是比較“唐突”的，這里有許多內容需要老師進行二次開發.

1.2讓數學名稱的來歷有根有據

孫維剛說:"科學上的任何規定都有為什么，數學尤其如此，世界上沒有沒有為什么的事."[2].然而實際教學中，很多學生問到數學名稱怎么來的時候，老師就用“這是規定，沒有為什么”來敷衍學生；其實，了解數學名稱的來歷，不僅有助于學生理解數學本質，也有利于提高學生學習的興趣.在“對數”的學習過程中，有必要讓學生了解相關名稱的來歷，以幫助學生理解知識的本質，比如為什么叫“真數”、“對數”？據考究，“對數”和“真數”的名詞跟納皮爾沒有什么關系，對數于康熙年間傳入中國，那時候對數的作用主要是將乘除運算化為加減運算，在整個運用對數進行計算的過程中，只有真數部分才是我們“真正計算的數”所以叫真數，而對數值只是起到一個橋梁的作用，所以對數最初叫“假數”，后來有了“真數和假數對列成表，故稱對數表”，往后“對數”這個詞越加深入人心，后來干脆稱假數為對數[3].有些問題，也可以準備一些數學史相關的資料留給學生課后閱讀，增加對知識來源的了解，以便更加準確地把握內容.

2　厘清研究問題的共性思維

很多時候，學生“會不會學”與老師“會不會教”是直接相關的，數學學習不是機械的模仿和訓練，重要的是要能夠基于理解的視角進行學習，也就是我們常說的“悟”——悟法、悟道，這種“悟”也不是什么“玄學”，而是體現在學習過程中的每一個環節，就看教師有沒有“法眼”，能夠揭示研究數學問題的共性思維，教給學生不僅僅是知識，而是思維、方法，研究數學問題的一般思路，也就是一種悟道的方法.

2.1讓學生體驗數學中研究新對象的一般思路

數學是思維的學科，只有在教學中揭示研究數學對象的基本方法，并提供機會讓學生進行反思總結，才能真正培養學生理性思維能力.對數是學生進入高中以來所遇到的第二個新對象(第一個是集合)，是一次讓學生體驗研究數學對象基本思路的良好時機，因此有必要經歷“背景(現實、數學內部)——定義——表示——分類——性質——運算——聯系和應用”的研究思路進行教學設計，并讓學生進行總結、反思，也只有站在“研究問題”的角度，才能更加好理解教材、使用教材，明晰教材內容編排的整體結構，有助于學生形成良好的學習習慣和思維能力.

2.2讓學生體驗數學中研究函數性質的一般思路

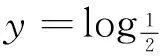
3　加強數學思想方法的滲透

又如，對數運算性質教學中，由MN=am+n得到loga(M·N)=m+n，即loga(M·N)=logaM+logaN既可以看作是對數定義的應用，也體現了“對數運算”的本質，將“乘法”化為“加法”，學習了函數之后，再從對數函數的性質的角度加以認識，就是f(MN)=f(M)+f(N)，這樣揭示運算的思想和函數思想去理解對數的運算性質，對學生理解知識本質是非常有幫助的.

4　對教材編寫的建議

在目前人教A版的教材中對知識、例題的處理，基本上都是“問題+解答”的模式，缺乏對問題的分析、總結反思、提煉，或者是部分具有代表性的問題，缺少了解決問題關鍵步驟的分析，對解決問題的示范效果打折扣.

4.1增加問題的分析與反思

教材例題本來就具基礎性、典型性和示范性的特征，這種典型，除了問題的代表性之外，解決問題的方法應該也具有典型示范的功能才是，所以對于部分例題，如果能夠增加一些分析性文字，解題后對解決問題的共性思維有總結提煉的話，對指導學生學習，養成良好的思維習慣會有很好的幫助.例如，在教材(人教A版必修1第72頁)“對數函數及其性質”中例8：“比較下列各組數中兩個值的大小：(1)log23.4,log28.5……”，建議教材增加“分析：比較兩個數的大小除了將兩個值計算出來再比較以外，往往可以轉化為兩個函數值的大小比較或者兩個函數圖像的位置關系，解決這類問題首先要將問題轉化為函數的語言進行描述，然后利用函數的圖像性質去解決.”進而解題過程可以這樣處理：log23.4,log28.5兩個對數值的底數相同，因此它們是函數f(x)=log2x自變量分別取x1=3.4,x2=8.5的兩個函數值，因為函數f(x)=log2x在(0,+∞)上是增函數，故f(3.4)

4.2呈現解決問題的步驟

根據例題的示范性功能，例題既是如何運用知識解題的典范也是思維訓練的典范，既是常規數學思維方法的典范又是如何解題思維的典范，即示范性主要體現在知識運用、數學方法和數學思維示范三個層面，因此建議教材要重視通過例題來揭示數學思維，呈現解題步驟來示范效果，對數在實際問題中的應用，教材P66例5和例6處理中，就可以增加“用數學模型解決實際問題”的基本步驟：

這樣左邊以流程圖的方式說明解決問題的思路，右邊是具體問題的解決過程操作步驟，這樣既直

觀明了，揭示分析問題、解決問題的基本思路和方法，揭示本質，又具有可操作性和思維示范作用.

[1]花奎.圍繞數學課堂教學中的本原性問題開展探究活動[J].中學數學研究(廣州)，2015,11.

[2]孫維剛.孫維剛談立志成才[M].北京：北京大學出版社，2006,8.

[3]郭龍先，劉秀.開辟大數計算新紀元——對數函數思想方法解析[J].昭通學院學報，2014,10.

[4]羅增儒.數學解題學引論[M].西安：陜西師范大學出版社，1997.

[5]陳永明工作室.數學習題教學研究[M].上海：上海教育出版社，2010,5.