再談一道填空題的另解及妙解*

江蘇省南京市第二十九中學　(210036)

郭建華

江蘇省南京市金陵中學　　　(210005)

于　健

?

再談一道填空題的另解及妙解*

江蘇省南京市第二十九中學(210036)

郭建華

江蘇省南京市金陵中學(210005)

于健

題目在ΔABC中，點D在邊BC上，且DC=2BD，AB∶AD∶AC=3∶k∶1，則實數k的取值范圍為_________.

文[1]從通觀全局，宏觀把握解題思路的角度探求該題的三種解法，強調對概念和通性通法的教學，很值得學習和研究.對此，在文[1]研究的基礎上筆者對該題又做了一些解法的探究和思考，供大家參考.

受文[1]解法2的啟發，將ΔABC放在坐標系中研究，根據題設條件，挖掘了問題的“隱性”軌跡，則使解題思路豁然開朗，于是得到下面的解法.

1　另解

解析：如圖1，以點A為原點，AB為軸建立平面

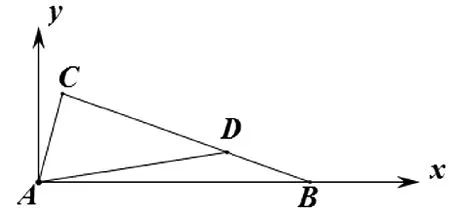
圖1

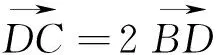
根據對題意的深刻理解和對圖形的觀察，通過添加輔助線的方法讓解題變得由難到易，由繁到簡，妙不可言，其解法如下.

2　妙解

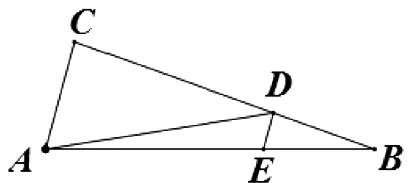
圖2

圓”，借助圓的定義及圓豐富的幾何性質，溝通條件和結論的關系，大大簡化計算過程，提高解題速度，事半功倍．在教師的引導下更多地為學生創造探究的元素，讓學生體會轉化思想在解題中的應用；“妙解”中通過數形結合，巧妙地添加輔助線，純粹運用平面幾何的相關知識求解，不僅提升解題的速度和準確度，而且使得解題過程更為簡捷明了.因此在解題中要不斷引導學生從不同角度分析問題，加強解題方法的對比，通過對題設條件的挖掘和再創造，尋求更好的求解方案.這樣不僅有利于培養他們的鉆研精神和創造能力，而且有利于思維靈活性的培養和陶冶他們的情操，體會數學給他們帶來的快樂.

[1]劉增娣.宏觀把握 追本溯源 讓解題思路自然而生[J].中學數學研究(江西)，2015(2)：34-36.

[2]郭建華.“設而不求”5例[J].數理天地，2016(3)：12-13.

[3]郭建華.重視借題“發揮 ”拓展數學思維[J].中學教研2015(12)：6-8.

江蘇省教育科學“十二五”規劃立項課題 ：信息技術環境下高中數學“問題—探究—解決”教學模式的應用研究 (D/2013/02/445)的研究成果之一.