智能算法用于汽油餾程蒸發溫度的計算

張柳鶯, 任瑩瑩

(中國石油化工股份有限公司廣東石油分公司，廣東　廣州　510000)

?

智能算法用于汽油餾程蒸發溫度的計算

張柳鶯, 任瑩瑩

(中國石油化工股份有限公司廣東石油分公司，廣東廣州510000)

探討了人工神經網絡法和徑向基神經網絡法，用于GB/T6536《石油產品蒸餾測定法》測定汽油餾程試驗時，從餾出溫度計算蒸發溫度的可能性。試驗表明，線性神經網絡法的泛化預測能力，優于徑向基神經網絡法。用所選的訓練集數據建立數學模型后，測試集數據的仿真結果表明，仿真值與原測定值的絕對偏差，沒有超過2 ℃，說明線性神經網絡法用于汽油蒸發溫度的計算是可行的，該方法是一種快速、準確、簡便值得借鑒的方法。

汽油餾程；蒸發溫度換算；線性神經網絡法；MATLAB

車用汽油規格指標中，要求用蒸發溫度表述其蒸發性能的優劣。通常汽油的蒸發溫度是采用GB/T6536-2010《石油產品蒸餾測定法》測定的。實驗中，使用測得的餾出溫度，通過換算，得到所需的各點蒸發溫度，過程較為繁瑣，給使用者帶來不便[1]。目前使用計算機的智能算法在眾多學科研究和工程應用中已得到廣泛應用，取得不少可喜的成果[2-4]。筆者嘗試在汽油餾程測定中，使用線性神經網絡(Linear Neural Networks，LNN)法完成各點餾出溫度到蒸發溫度的計算。試驗表明，LNN法用于汽油餾程蒸發溫度計算是可行的，該方法具有快速、簡便、準確的特點，是一種值得借鑒的方法。

1　實　驗

1.1儀器設備與試樣

德國海爾潮 PAC OPTIDIST型自動餾程測定儀；大氣壓力計。

油品93#、97#車用汽油。

1.2實驗過程

按照GB/T6536《石油產品蒸餾測定法》來測定其餾程，記錄初餾點(initial boling point, ibp)、5%、10%、20%、30%、40%、50%、80%、90%、95%和終餾點(final boling point, fbp)的餾出溫度，記錄測試現場的大氣壓，并按照規程的要求，求出蒸發損失量等數據，最后按照規程指定的方法，計算出要求的各點蒸發溫度[1]。

用LNN法計算各點的蒸發溫度時，是將訓練集的ibp、10%、50%、90%、fbp的餾出溫度、蒸發損失量和測定時的大氣壓數據，作為輸入向量，將上述各點對應的蒸發溫度作為目標向量，輸入到預先安裝了MATLAB軟件的計算機中，用其中的神經網絡工具箱中的LNN網絡函數，建立數學模型，然后用測試集數據考察模型的“泛化”預測能力，模型泛化能力滿意時，就可以在實際測定時，用來仿真預測上述各點的蒸發溫度。

2　結果與討論

2.1智能算法的優越性及方法的選擇

智能算法是一種高效的信息處理技術，解決了眾多學科研究和工程應用中許多重要問題。它是從已知的數據出發，運用當今新技術、新理論，如支持向量機、神經網絡、決策樹、粗糙集理論、模糊集理論和智能仿生計算等，提取其中的特征量，然后再進行特征抽取以確定合適的特征量，張成模式空間或特征空間，最后通過智能算法進行訓練和判別，來揭示已知數據信息中隱含的性質和規律，為人們提供有用的決策依據和過程優化的重要信息[2-3]。

正是智能算法在解決信息處理方面的優越性，筆者確定在汽油餾程測定中，嘗試使用人工神經網絡中的LNN網絡；徑向基神經網絡的廣義回歸(newgrnn)網絡來建立數模和仿真。實驗表明，LNN法建立的模型，泛化預測能力強，是一種快速、準確、簡便預測汽油餾程蒸發溫度可借鑒的方法[5]。

2.2人工神經網絡

2.2.1人工神經網絡簡介

人工神經網絡是一類模擬人腦功能的全新數據和知識等信息處理加工系統，是由人工建立的以有向圖為拓撲結構的動態系統，通過對連續或斷續的輸入作狀態響應而進行信息處理。神經網絡的數學模型是人工神經網絡的理論基礎。1943年以來，經過了漫長、曲折的發展過程，如今已成為解決復雜信息處理問題，如模式識別、預測、圖像處理、函數擬合、優化等的有力工具。

人工神經網絡的結構由接收信號的輸入層、輸出信號的輸出層及處于輸入層和輸出層之間的隱含層組成。人工神經網絡的運行可分為兩個階段：①訓練或學習階段；②預測(推廣)階段。在訓練或學習階段，反復向神經網絡提供一系列輸入—輸出模式，并不斷調整節點之間的相互連接權重，直至特定的輸入產生期望的輸出。通過學習或訓練后，神經網絡便具備(學會)了正確的輸入輸出響應行為，從而對未知樣本進行預報。

2.2.2MATLAB神經網絡工具箱概述

MATLAB神經網絡工具箱是用MATLAB語言構造出的典型神經網絡激活函數,使得人們對所選定網絡輸出的計算，變成了對激活函數的調用，并按照各種典型的修正網絡權重的規則，結合網絡的訓練過程，用MATLAB編寫出各種網絡設計與訓練的子程序，從而可根據自己的需要，調用所需函數解決實際問題。主要包括的網絡模型有：①感知器；②線性網絡；③BP網絡；④徑向基函數；⑤自組織網絡；⑥回歸網絡。對于各種網絡模型，工具箱集成了多種學習算法，還給出了大量的示例程序，為用戶提供了極大方便。

2.2.3MATLAB神經網絡工具箱的應用

實踐中常發現，用各種智能方法建立的數學模型對已知數據(即所謂訓練集)常能擬合較好，而預報未知樣本時，偏差會較大，這就是所謂的“過擬合”(overfiing)現象。反之，由于樣本數目過少，建立的模型精度不夠，則稱之為“欠擬合”(underfiing)。如何提高算法和數學模型的推廣能力，以確保預

報結果的可靠性，顯然是智能算法中的重要課題。實踐表明，用智能算法的神經網絡法求解，一是應根據問題的特點選擇合適的網絡模型；二是建立網絡模型時通過仿真，分析判斷網絡是否適合實際問題的特點，是否達到所需的準確度和精度，這兩點至關重要[2-5]。

筆者用神經網絡法由汽油餾出溫度計算其蒸發溫度時，曾選擇了LNN網絡；徑向基神經網絡中的廣義回歸(newgrnn)網絡，實驗證明，用LNN網絡建立的模型，泛化預測能力優于后者。

2.2.4LNN法計算汽油餾程的蒸發溫度

2.2.4.1LNN網絡簡介

LNN網絡結構如圖1所示，它是一種最簡單的神經元網絡，由一個或多個線性神經元組成，每個神經元的傳遞函數為線性函數，可采用Widrow-Hoff學習規則或者LMS(Least Mean Square)算法來調整網絡的權重和閾值。

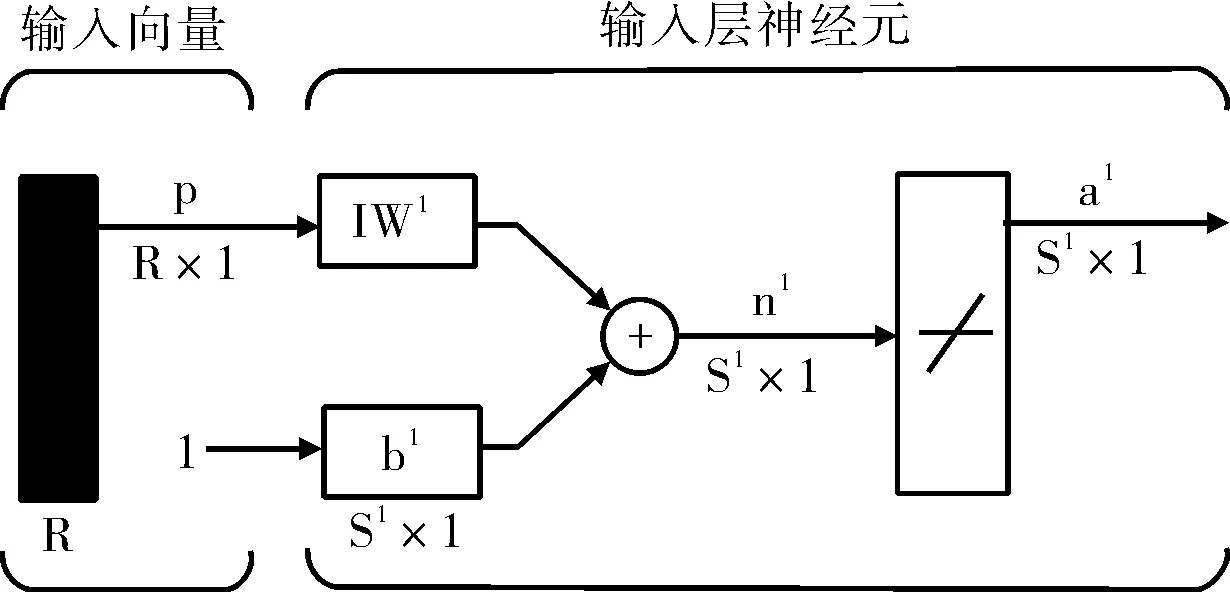
圖1　線性神經網絡層模型結構圖

LNN網絡的神經元的傳輸函數是線性函數，LNN網絡層的輸出為：

a=purelin(WP+b)=WP+b

LNN網絡層的輸出可以取任意值，而且線性神經元網絡可以是多層的。LNN網絡只能求解線性問題，而不能用于非線性計算，這一點與BP網絡和徑向基網絡不同[6-7]。

本文采用newlind函數設計LNN網絡。調用格式為：

net=newlind(P,T)

其中：P為訓練集網絡的輸入向量，T為訓練集網絡的目標向量。

2.2.4.2用LNN法計算汽油餾程的蒸發溫度

(1)訓練集、測試集試樣的確定

取車用汽油餾程測定數據64組，選1～45組作為訓練集樣本，用來訓練建立數學模型，選46～64組共19組作為測試集樣本，考察模型的泛化預測能力，見表1、表2。表中餾出溫度、蒸發損失量和大氣壓，為試驗測定獲得，蒸發溫度是按照GB/T6536方法規定得來。

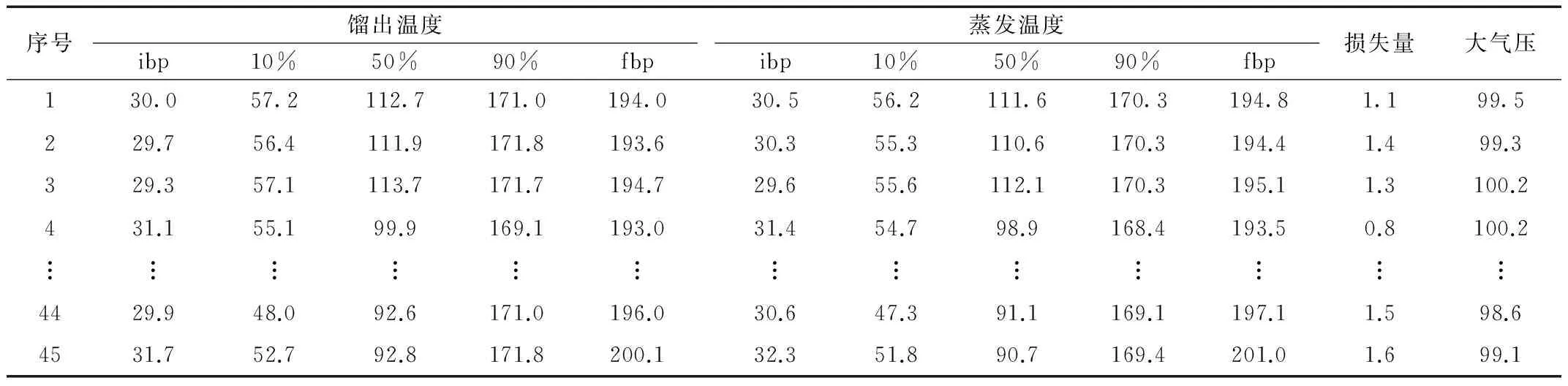
表1　汽油餾程訓練集樣本數據

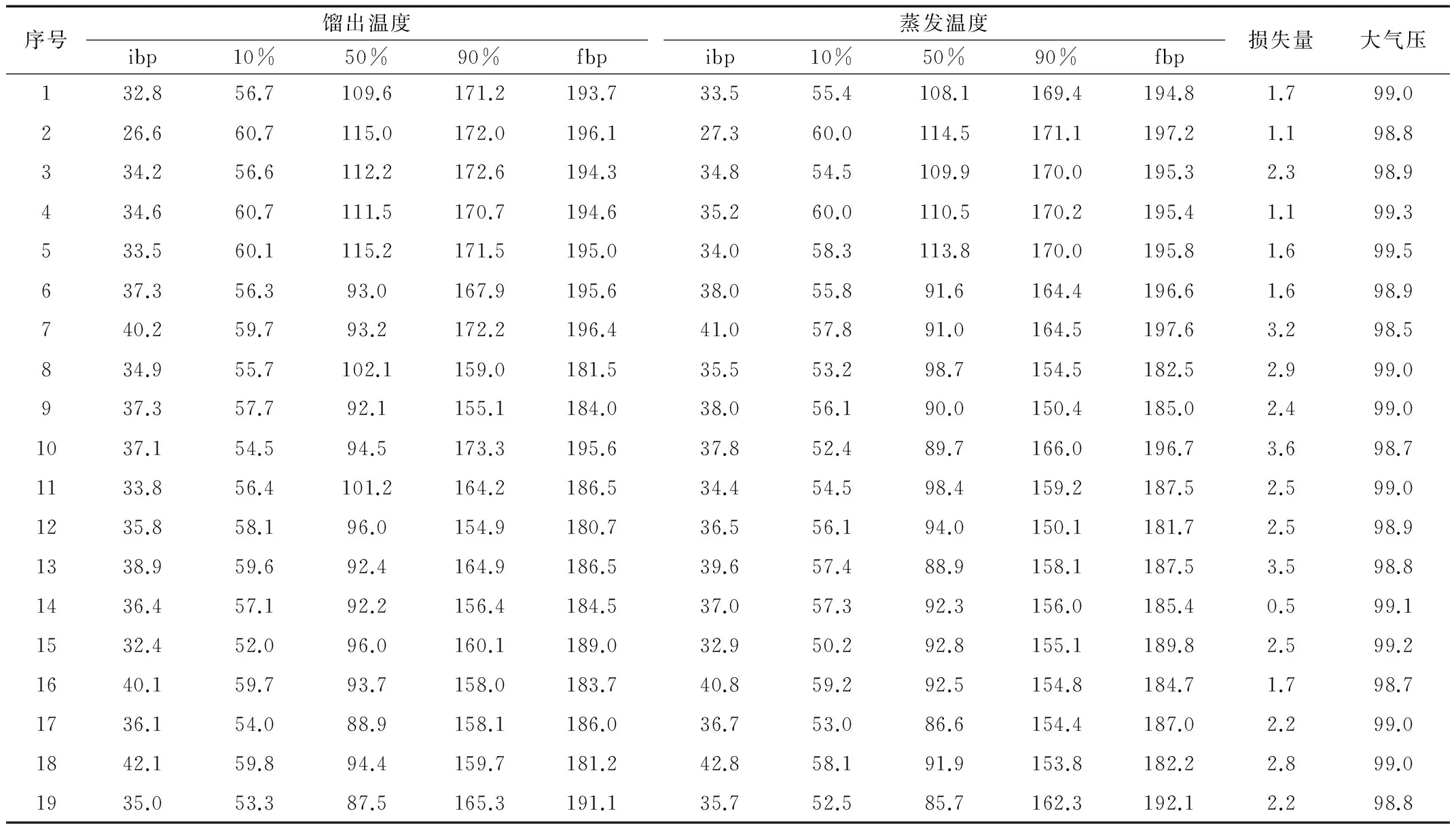
表2　汽油餾程測試集樣本數據

(2)LNN算法

用GB/T6536方法從餾出溫度計算蒸發溫度時，考慮了蒸發損失量和測定時大氣壓的影響[1]，因此在設計LNN網絡結構建立數模時，也考慮了餾出溫度、蒸發損失量和測定時大氣壓的影響。程序設計時，依次把訓練集的ibp、10%、50%、90%和fbp點的餾出溫度和損失量及大氣壓作為輸入向量，把上述各點的蒸發溫度作為目標向量，選擇newlind函數設計網絡結構，用sim函數仿真，通過訓練網絡和仿真即可預測蒸發溫度。例如將訓練集的10%點餾出溫度、蒸發損失量和大氣壓作為輸入向量，將對應的10%點蒸發溫度作為目標向量，輸入電腦，選擇newlind函數建立網絡，用sim函數仿真，再用測試集的10%點對應的數據考察數模的泛化預測能力，如果對建立的數模滿意，就可以在以后測定時，用來預測10%點的蒸發溫度。

(3)測試集樣本仿真結果與GB/T6536方法測定結果對比

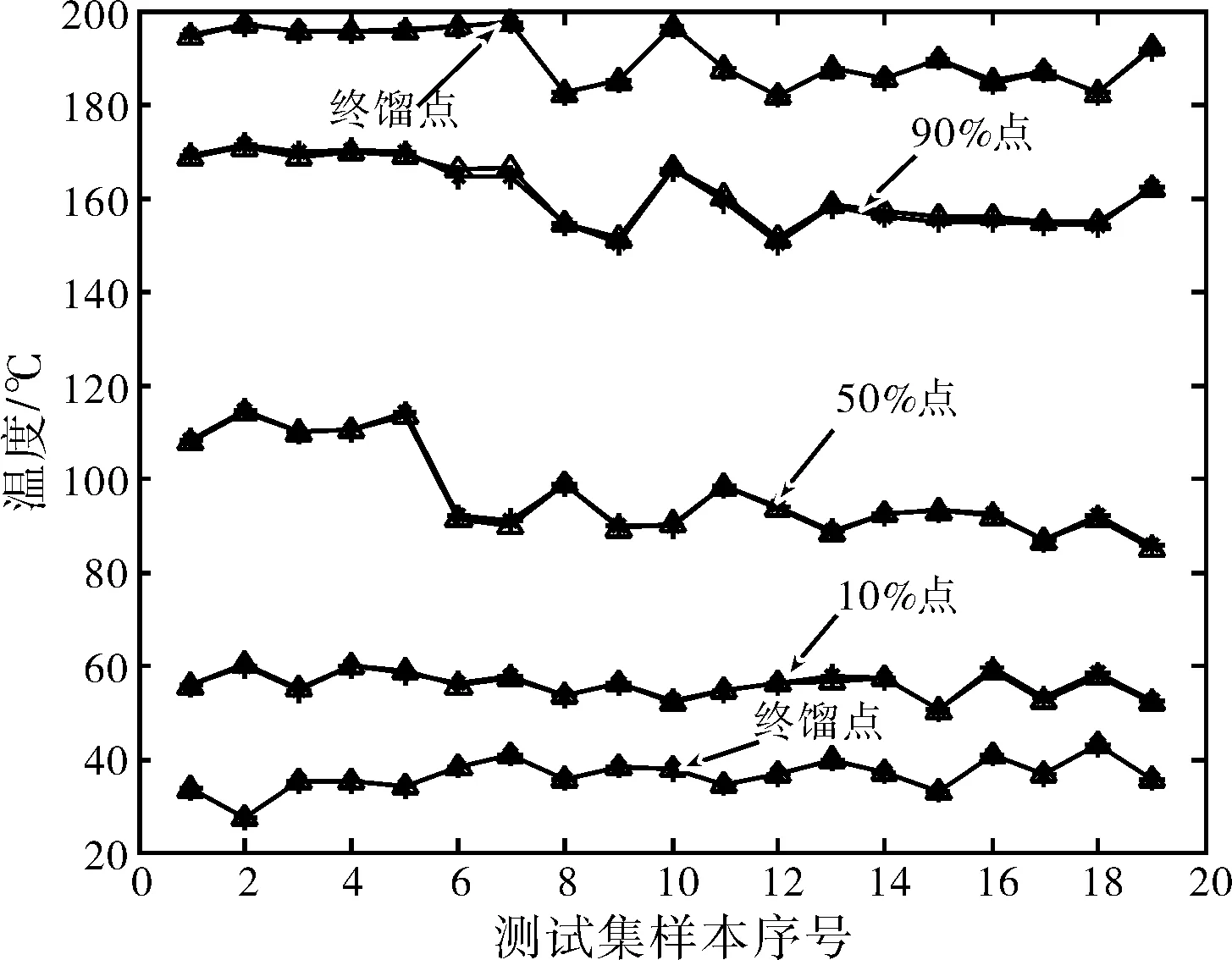
圖2　測試集樣本各點蒸發溫度實測值與仿真值對比圖

對比結果見圖2。由圖2可見，除過90%點的實測值與仿真值偏差稍大以外，ibp、10%、50%、fbp實測值與仿真值偏差均很小。表3列出了測試集樣本各點蒸發溫度實測值與仿真值的最大絕對偏差，由表3可見，90%點實測值與仿真值偏差稍大，但也未超過2 ℃。

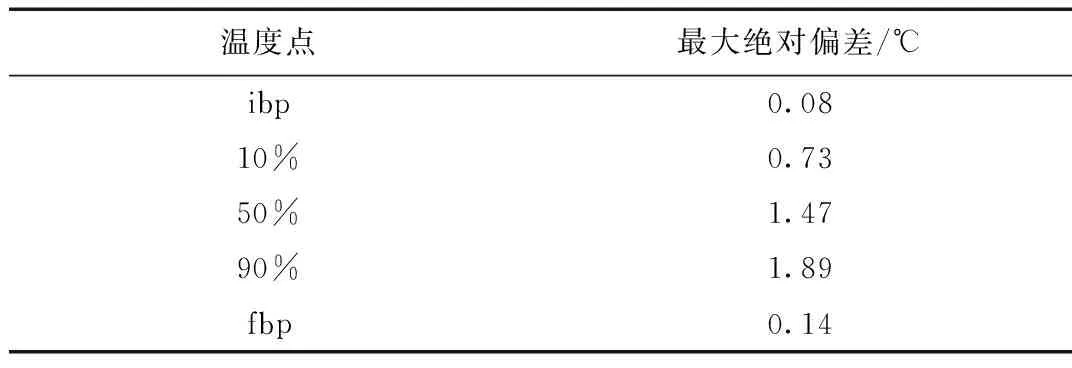
表3　測試集各點蒸發溫度實測值與仿真值的最大絕對偏差

(4)LNN法測定結果與徑向基廣義回歸網絡法結果的比較

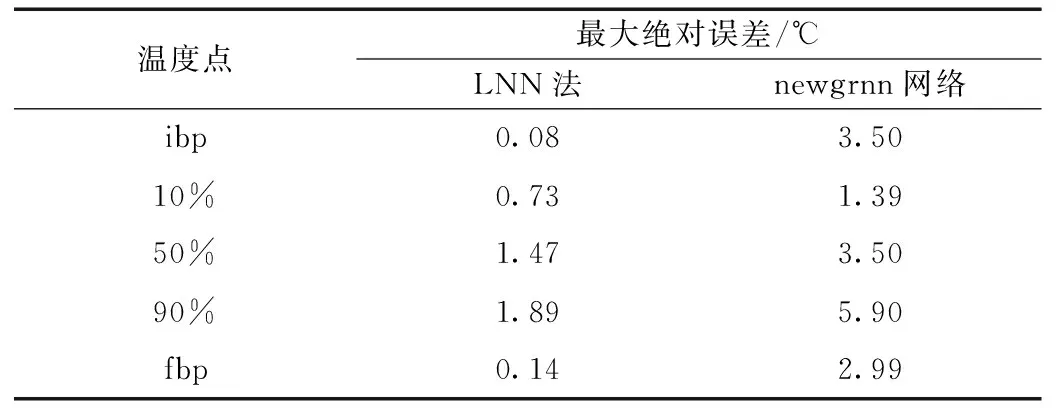
表4　LNN法仿真結果與徑向基廣義回歸網絡法仿真結果比較

表4為LNN法測定結果與徑向基廣義回歸網絡法結果的比較表。由表可見，LNN法的仿真值與徑向基廣義回歸網絡法仿真值比較，前者要優于后者。

(5)LNN法測試的精密度考察

表5為精密度考察表。根據理論分析，汽油餾程蒸發溫度測定精密度主要取決于測定過程，而計算機仿真環節，不會帶來多大誤差，所以測定的精密度和手工測定的精密度相當。

表5　汽油餾程蒸發溫度測定精密度考察表(n=5)

注：n=5表示實驗時進行了5次平行實驗。

3　結　論

(1)實驗表明，在使用GB/T6536測定汽油餾程，由餾出溫度換算成蒸發溫度時，可以使用LNN法。使用時只需要向計算機輸入ibp、10%、50%、90%和fbp的餾出溫度，蒸發損失量以及測試時的大氣壓，然后用建立好的線性網絡仿真，就可以快速、簡便、準確預測出所需的餾程蒸發溫度，因此這是一種計算蒸發溫度的值得借鑒的方法。

(2)使用人工神經網絡法建立數學模型時，一是要注意選擇合適的網絡模型，二是要調整好網絡參數，這樣才可以建立泛化預測能力強的數學模型，取得滿意的仿真預測結果。

(3)使用LNN法計算餾程蒸發溫度，由于觀察的溫度點減少，操作者工作強度減小，很適合手工操作。

(4)當建立的數學模型使用一段時間后，例如一周或半個月，需要跟使用GB/T6536方法計算的蒸發溫度進行對照，對數學模型進行校準、修正，以保證仿真預測結果的可靠性。

[1]國家技術監督局.GB/T6536-2010 石油產品蒸餾測定法[S]．

[2]許國根.模式識別與智能計算的MATLAB實現[M].北京:北京航空航天大學出版社, 2012:5-8.

[3]楊淑瑩.群體智能與仿生計算—MATLAB技術實現[M].北京:電子工業出版社, 2012:15-18.

[4]楊淑瑩. 模式識別與智能計算—MATLAB實現[M].北京:電子工業出版社, 2008:17-20.

[5]許國根.化學化工中的數學方法及MATLAB實現[M].北京:化學工業出版社, 2008:2-6.

[6]周開利.神經網絡模型及其MATLAB仿真程序設計[M].北京:清華大學出版社, 2005:10-11.

[7]李水祥,謝文武. MATLAB語言的神經網絡工具箱及應用[J]. 高等函授學報(自然科學版), 2007,20(1):43-46.

Calculation of the Evaporation Temperature of Gasoline Distillation by Intelligent Algorithm

ZHANGLiu-yimg,RENYing-ying

(Guangdong Petroleum Company, China Petroleum Chemical Co., Ltd., Guangdong Guangzhou 510000, China)

The method of artificial neural network and radial basis function neural network method was discussed, used for the determination of gasoline distillation test GB/T6536 "Petroleum Products-Determination of distillation", calculating the possibility of evaporation temperature from the distillation temperature. Experiments showed that the generalization of linear neural network prediction ability was better than the RBF neural network. Data was set to establish the mathematical model with the selected training set, test data and simulation results showed that the simulation values of absolute deviation and the original values, was no more than 2 ℃, and it showed that the linear neural network method for calculating the evaporation temperature was feasible, the method was a rapid, accurate, simple and valuable method.

gasoline distillation; evaporation temperature conversion; linear neural network; MATLAB

張柳鶯(1981-),女，大學本科，從事油品質檢技術工作。

A

1001-9677(2016)010-0134-04