一類空間直線方程問題的多種求解方法

劉春輝

（赤峰學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)學(xué)院，內(nèi)蒙古赤峰024000）

一類空間直線方程問題的多種求解方法

劉春輝

（赤峰學(xué)院數(shù)學(xué)與統(tǒng)計學(xué)學(xué)院，內(nèi)蒙古赤峰024000）

綜合運(yùn)用空間解析幾何、微積分、線性代數(shù)和向量代數(shù)的思想及運(yùn)算技巧，討論一類空間直線方程的求解問題，從不同角度給出了解決該類問題的多種方法.

空間解析幾何；直線方程；向量

1　引言

空間直線作為空間曲線的一種最特殊和最簡單的類型，是高等數(shù)學(xué)[1]課程體系中關(guān)于空間解析幾何與向量代數(shù)內(nèi)容的重要組成部分.在這部分內(nèi)容中，空間直線方程的求取毋庸置疑的是問題的核心和基礎(chǔ).同時，縱觀種類繁多的關(guān)于高等數(shù)學(xué)和空間解析幾何[2]的教材和教學(xué)參考書，其中不乏對空間直線方程求解問題的分析和討論.就同一類問題而言，如果從多角度多側(cè)面去進(jìn)行分析，不但可以得到多種不同的解決問題的方法，而且也有助于培養(yǎng)學(xué)生綜合運(yùn)用知識的思維能力和創(chuàng)新能力.

鑒于此，本文針對如下一類空間直線方程的求解問題，從多個角度進(jìn)行分析和思考，獲得了該類問題的多種解決方法.

問題設(shè)空間直線l經(jīng)過空間一點P(x0,y0,z0)且與兩平面的交線平行，求直線l的方程.

2　問題的多種解決方法

分析已知條件，不難看出問題的關(guān)鍵在于確定直線的方向向量s=(m,n,p)，從而得到l的點法式方程：方法一利用向量積的特征求直線方程因為平面π1和π2的法向量分別為：

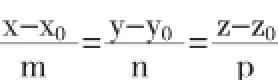
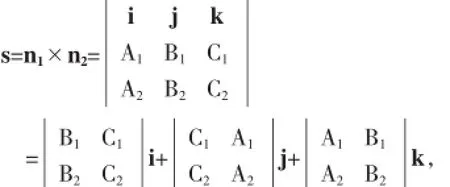
且l與平面π1和π2的交線平行，所以l的方向向量s必同時與π1和π2的法向量垂直，即

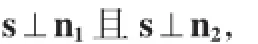
故根據(jù)兩個向量向量積的特征，可取

于是可得l的方向向量

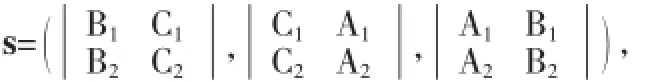
因此，空間直線l的方程為

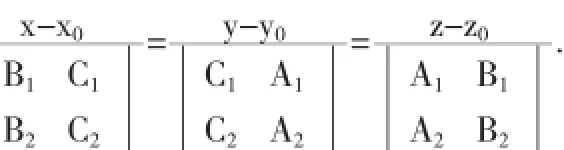
方法二利用解線性方程組的Gramer法則求直線方程

引理1[1,2]設(shè)向量a=(a1,a2,…,an)，b=(b1,b2,…,bn)則a⊥b當(dāng)且僅當(dāng)a·b=0當(dāng)且僅當(dāng)a1b1+a2b2+…+anbn=0.

引理2[3](Gramer法則)設(shè)一個含有n個未知量n個方程的線性方程組為

它的系數(shù)行列式為

其中Dj是把行列式D的第j列的元素?fù)Q以方程組的常數(shù)項b1,b2,…,bn而得的n階行列式.

下面利用Garmer法則給出所討論問題的另一種解決方法：

因為平面π1和π2的法向量分別為：

且l與平面π1和π2的交線平行，所以l的方向向量s必同時與π1和π2的法向量垂直，即

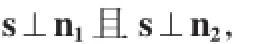
故由引理1，可得以m,n,p為未知量的方程組

當(dāng)D≠0時，該方程組有且僅有一個解

又因為π1∩π2≠?，n1⊥π1且n2⊥π2，所以n1與n2不平行，從而它們的對應(yīng)分量不成比例，不妨假設(shè)

于是將方程組（1）中未知量p看成任意常數(shù)，變形得以m,n為未知量的方程組

其系數(shù)行列式

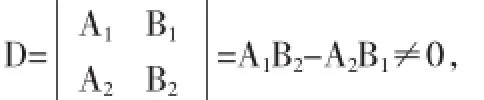
故由Garmer法則知，方程組（2）有唯一解

注意到常數(shù)p的任意性，令

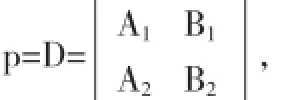
便得l的方向向量

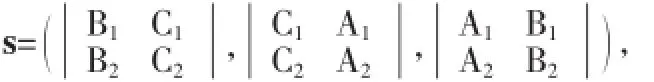
因此，空間直線l的方程為

點M(x0,y0,z0)∈Γ，又設(shè)三元函數(shù)F和G對各個自變量x,y,x都具有連續(xù)的偏導(dǎo)數(shù)且雅可比行列式

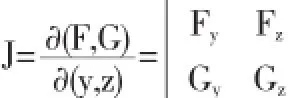
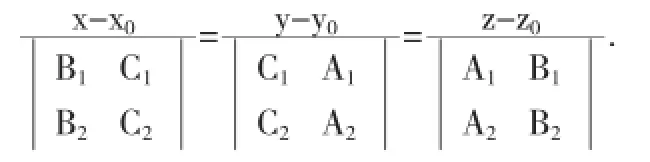
方法三利用隱函數(shù)組的存在性求直線方程引理3[1]設(shè)空間曲線Γ的一般方程為

滿足J|M≠0，則在點M的某個鄰域U(M)內(nèi)，由(3)式可唯一的確定一組一元函數(shù)

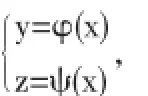
且Γ上任意一點P(x,y,z)處的切向量為

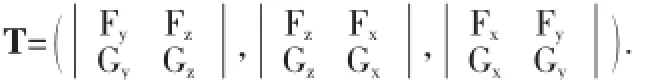
下面利用引理3給出所討論問題的另一種解決方法：

首先令

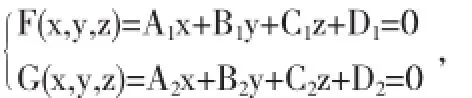
因為π1∩π2≠?，n1⊥π1且n2⊥π2，所以n1與n2不平行，從而它們的對應(yīng)分量不成比例，不妨假設(shè)

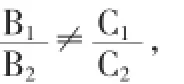
則雅可比行列式滿足

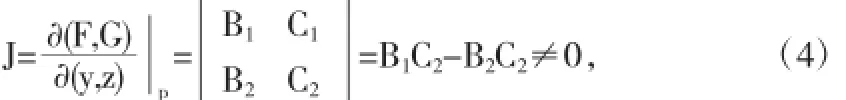
故由引理3得l的方向向量

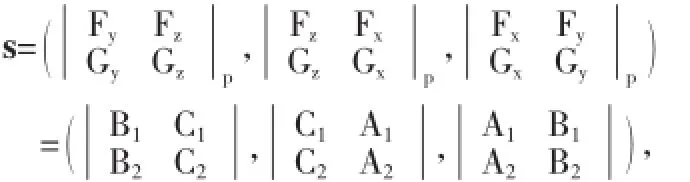
因此，空間直線l的方程為

注在上述過程中，如果（4）式滿足J=0，而由π1∩π2≠?，n1⊥π1且n2⊥π2知

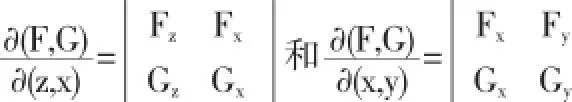
在P點處的值至少有一個不為0，因此利用引理3同樣類似可得上述結(jié)論.

至此，我們分別利用向量積的特征、Garmer法則和隱函數(shù)組的存在性獲得了解決所論問題的三種方法，最終都得到了直線的點法式方程的求解公式.如果考慮到兩個平面平行的特征，還可獲得所論問題的一種更簡單的解決方法.

方法四利用空間平面平行的特征求直線方程

引理4[1,2]設(shè)空間兩個平面為

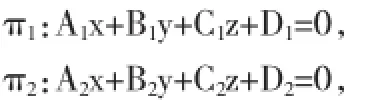
則π1與π2平行的充要條件是

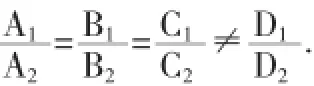
利用引理4給出所討論問題的一種更簡單的解決方法：

因為過點P(x0,y0,z0)且平行于平面π1：A1x+B1y+C1z+D1=0的平面為

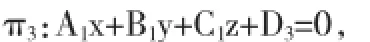
其中D3=-(A1x0+B1y0+C1z0)且D3≠D1.

過點P(x0,y0,z0)且平行于平π2：A2x+B2y+C2z+D2=0的平面為

其中D4=-(A2x0+B2y0+C2z0)且D4≠D2.又因為π1∩π2≠?，所以π3∩π4≠?.

因此，注意到P(x0,y0,z0)∈π3∩π4便得平面π3與π4的交線即為所求直線l，即空間直線l的方程為

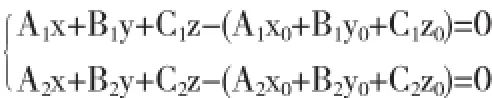
3　結(jié)束語

通過上述討論，不難看出，雖然四種方法考慮問題的角度與出發(fā)點各不相同，但是殊途同歸，最終獲得的結(jié)論是一致的，這正是數(shù)學(xué)問題一題多解的精髓所在.問題的思考與解決的過程，不僅可以讓我們不斷開拓思維，使思考問題的思路更加靈活，而且有助于我們進(jìn)一步理清前后知識的脈絡(luò)，達(dá)到融會貫通的效果.

〔1〕同濟(jì)大學(xué)數(shù)學(xué)系.高等數(shù)學(xué)：下冊[M].第七版.北京:高等教育出版社,2014.

〔2〕李養(yǎng)成.空間解析幾何[M].新版.北京:科學(xué)出版社,2007.

〔3〕王萼芳,石生明.高等代數(shù)[M].北京:高等教育出版社, 2003.

O182.2

A

1673-260X（2016）03-0003-02

2015-12-09