基于塊剪枝多路徑匹配追蹤的多信號聯合重構

司菁菁, 候肖蘭, 程銀波

(燕山大學信息科學與工程學院, 河北 秦皇島 066004)

?

基于塊剪枝多路徑匹配追蹤的多信號聯合重構

司菁菁, 候肖蘭, 程銀波

(燕山大學信息科學與工程學院, 河北 秦皇島 066004)

針對多路徑匹配追蹤(multipath matching pursuit,MMP)無法利用稀疏信號的結構信息、迭代層數較高時計算復雜度較大等問題,提出了一種適用于重構塊稀疏信號的塊剪枝多路徑匹配追蹤算法。該算法以原子塊作為路徑擴張的節點,在一定迭代層數后引入剪枝操作,極大地降低了數據運算量。進而,針對多觀測向量(multiple measurement vector,MMV)問題,提出了MMV塊剪枝MMP算法,用以實現無線傳感網小范圍內多傳感器信號的聯合重構。實驗表明,塊剪枝MMP的重構性能優于MMP,MMV塊剪枝MMP的聯合重構性能優于MMV塊A*正交匹配追蹤、MMV子空間匹配追蹤和MMV正交匹配追蹤。

分布式壓縮感知; 多觀測向量; 塊稀疏; 多路徑匹配追蹤

0　引　言

物聯網是當今信息科學領域一個迅速發展的新方向。無線傳感器網絡(wireless sensor networks,WSN)作為物聯網的重要支撐,近年來受到了業界研究者的廣泛關注。WSN通過布置在一定區域內的多個傳感器節點組成網絡,靈活方便地監測區域內的環境變化,在軍事、民用、環境監測等領域具有重要的實際應用價值。然而,節點資源(能量、存儲空間、計算能力等)有限是限制WSN應用的一個主要因素。如何降低WSN中數據采集與傳輸的資源消耗是一個值得深入研究的問題。

分布式壓縮感知(distributed compressed sensing,DCS)[1]將適用于單個信號壓縮與重構的壓縮感知(compressed sensing,CS)理論擴展到多個信號,實現了多信號的分布式壓縮與聯合重構。DCS技術的應用能夠有效減少WSN中的數據采集量,從而節約存儲空間,提高傳輸效率,降低數據采集與傳輸過程中的能量消耗[2]。

多觀測向量(multiple measurement vector,MMV)問題[3-4]是DCS理論的一個重要研究方向,解決的是具有相同支撐集的多個稀疏信號的聯合重構問題。在WSN小范圍內,多個傳感器檢測到的溫度、濕度等信號通常具有很強的相關性,在利用稀疏基(例如小波基)表示時,它們的顯著系數通常出現在大致相同的位置處。可見,WSN小范圍內多傳感器采集信號的聯合重構問題可以看作是一個MMV問題。另一方面,傳感器采集信號在稀疏基上通常是塊稀疏的,即非零系數是成簇出現的[5]。因此,針對MMV問題的塊稀疏信號聯合重構算法的研究在WSN中具有重要的實際應用價值。

貪婪迭代算法因其具有重建速度快等優點,成為實用研究中最受關注的一類CS重建算法。在標準CS理論下,針對塊稀疏信號的貪婪迭代類重構算法有塊稀疏匹配追蹤(block matching pursuit,BMP)算法、塊稀疏正交匹配追蹤(block orthogonal matching pursuit,BOMP)算法[6]、基于約束等距的塊稀疏匹配追蹤算法[7]、非均勻塊稀疏信號盲重構算法[8]、塊A*正交匹配追蹤(block A*orthogonal matching pursuit,BA*OMP)算法[9]、子空間匹配追蹤(subspace matching pursuit,SMP)算法[10]等。然而,目前針對MMV問題的貪婪迭代類塊稀疏信號聯合重構算法僅僅有較少文獻提及。文獻[9]將BA*OMP算法應用于MMV問題,提出了MMV塊A*正交匹配追蹤(BA*OMP for MMV,BA*OMPMMV)算法。文獻[11]針對塊稀疏信號,將SMP算法分別應用到MMV模型和廣義多觀測向量(generalized multiple measurement vector,GMMV)模型中,提出了SMP-MMV算法和SMP-GMMV算法。

本文首先針對塊稀疏信號的重構問題,在多路徑匹配追蹤(multipath matching pursuit,MMP)算法[12]的基礎上,提出了塊剪枝多路徑匹配追蹤(block pruning multipath matching pursuit,BPMMP)算法。該算法利用了塊稀疏信號的結構信息,在獲得良好重建效果的同時,極大地降低了數據處理量,既適用于信號塊稀疏度已知的情況,也適用于塊稀疏度未知的情況。進而,針對MMV問題提出了MMV塊剪枝多路徑匹配追蹤(block pruning multipath matching pursuit for MMV,BPMMPMMV)算法,用以實現WSN小范圍內多傳感器信號的聯合重構。利用合成信號和Intel Berkeley Research Lab[13]的WSN實測溫度信號進行的仿真實驗表明,BPMMP算法的重構性能優于MMP算法,BPMMPMMV算法的聯合重構性能優于BA*OMPMMV、SMP-MMV和MMV正交匹配追蹤 (orthogonal matching pursuit for MMV, OMPMMV)算法[14],且其運行時間顯著低于BA*OMPMMV、SMP-MMV和SMP-GMMV。

1　MMV問題和塊稀疏信號

1.1MMV問題

MMV問題解決的是具有相同支撐集的多個稀疏信號的聯合重構問題[15]。設n個共享支撐集的稀疏信號構成信號集X=[x1,x2，…,xn]∈RN×n,觀測矩陣A∈RM×N。多觀測向量Y=[y1,y2,…,yn]∈RM×n可表示[3]為

Y=AX

(1)

式中,xi和yi分別表示X和Y的第i(i=1,2,…,n)列;N和M分別表示每個信號xi的維數和每個觀測向量yi的維數。

任何MMV問題都可以通過奇異值分解和降維操作轉換為標準形式的MMV問題[15]。

(2)

式中,‖X‖0=|suppX|,多觀測向量Y是滿秩的,即rank(Y)=n≤‖X‖0。

當考慮噪聲時,MMV模型可表示[15]為

(3)

式中,E∈RM×n表示觀測噪聲。

1.2塊稀疏信號

在信號處理領域的許多實際應用問題中,稀疏信號中的非零值、零值是成塊出現的,稱這類信號為塊稀疏信號[16-18]。為定義塊稀疏,將信號x表示[9]為

(4)

式中,d表示塊的長度;P表示塊的數量;x[p]表示第p(p=1,2,…,P)塊;N=Pd。若x中非零塊的個數為K,則稱信號x是塊K稀疏的[16]。當d=1時,塊稀疏信號等同于普通的稀疏信號。

當對形如式(4)所示的塊稀疏信號進行壓縮感知觀測時,對觀測矩陣A進行相應劃分[9]。

(5)

式中,ai表示A的第i(i=1,2,…,N)列;A[p]表示A的第p(p=1,2,…,P)列塊(原子塊)。

2　BPMMPMMV算法

MMP算法用節點代表一個原子,用路徑代表用以重構原始信號的候選原子子集(以原子索引集合的形式表示),將最優路徑的搜索問題建模成組合學中的樹形搜索問題,并基于貪婪迭代算法實現最優路徑的快速搜索。MMP算法的重構性能優于正交匹配追蹤 (orthogonalmatchingpursuit,OMP)、分段式正交匹配追蹤 (stagewiseorthogonalmatchingpursuit,StOMP)、子空間追蹤 (subspacepursuit,SP)等經典CS重構算法[12]。然而,MMP算法需要事先確知信號的稀疏度,且當信號稀疏度較大時,迭代層數較多、候選路徑較多、計算復雜度較高。另一方面,MMP算法無法利用信號的結構稀疏信息,不適用于塊稀疏信號的重構。此外,在實驗中發現,MMP算法在一定迭代層數之后,一些候選路徑雖然已經明顯呈現出重建殘差較大的問題,但是迭代過程依然會義無返顧地為這些路徑搜索下一原子,實現路徑擴展,而這些路徑在最后一層對應的候選路徑一般也具有較高的重建殘差,不會成為最優解。可見,在迭代搜索過程進行到一定程度之后,那些已經表現出重建性能不佳的路徑,若繼續參加迭代,不但對最終的重建結果沒有太大幫助,反而浪費了大量的運算時間與數據存儲空間。針對以上問題,本文在MMP算法的基礎上引入樹枝修剪操作,提出了適用于塊稀疏信號重構的BPMMP算法。

2.1BPMMP算法

BPMMP算法將觀測矩陣劃分成長度相等、重疊長度相等的原子塊,以原子塊為單位進行路徑擴張。用路徑代表重構原始信號的候選原子塊集合(以原子塊索引集合的形式描述)。結合基于樹形結構的路徑擴張與貪婪迭代算法,實現重建原始信號的最優原子塊集合的快速搜索。在迭代層數達到Γ值之后,對搜索樹進行剪枝操作,根據重建殘差對當前層搜索到的候選路徑進行篩選,去掉1/α比例沒有希望成為最優解的候選路徑,使它們不參加后續層的路徑擴展,有效減少運算時間與存儲空間的浪費。

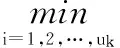
MMP算法和BPMMP算法的計算量均主要集中于觀測矩陣與重建殘差的乘積。此矩陣與向量乘積的計算次數取決于迭代層數和每層候選路徑的數量,而迭代層數與信號的稀疏度有關。設塊稀疏信號x的稀疏度為K*、塊稀疏度為K,K*>K。利用MMP算法與BPMMP算法重建x的平均迭代層數分別為O(K*)和O(K)。在第k層迭代中(k≥Γ),MMP和BPMMP算法的最大候選路徑數分別為Lk和Lk(1-1/α)k-Γ。每條候選路徑在進行擴張時最多需要M×N次乘法運算。可見,MMP的復雜度為O(MNK*LK*),而BPMMP的復雜度為O(MNKLK(1-1/α)K-Γ),明顯低于MMP。

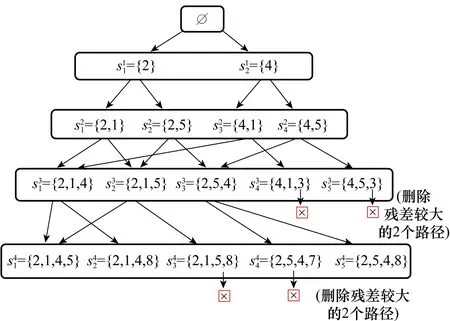
圖1　BPMMP算法樹形搜索結構與剪枝操作舉例Fig.1　An example of tree-structured path searching and pruning in BPMMP

2.2BPMMPMMV算法的實現

為了求解塊稀疏信號的MMV問題,本文在BPMMP算法的基礎上,進一步提出了BPMMPMMV算法。該算法利用了BPMMP算法的路徑擴張與剪枝機制,但針對MMV問題的求解,對原子塊選擇、信號集重構以及殘差更新等操作進行了修改。

(6)

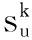
(7)

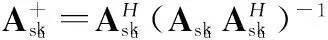
此外,在求取最小殘差路徑、剪枝篩選路徑、判斷迭代停止條件等操作中,BPMMPMMV算法均針對MMV模型,利用Frobenius范數代替了BPMMP算法中的歐幾里得范數。

BPMMPMMV算法的偽代碼如表1所示。

表1　BPMMPMMV算法的偽代碼

3　實驗結果及分析

編寫Matlab仿真程序,分別利用隨機合成信號和WSN中多傳感器的實測溫度信號測試本文提出的BPMMP算法和BPMMPMMV算法的重構性能,并分別與MMP、SMP、BA*OMP算法和OMPMMV、BA*OMPMMV、SMP-MMV、SMP-GMMV算法進行比較。仿真計算機的硬件配置為CPUAMDathlon(tm)×255,主頻3.11GHz,內存1.75GB。軟件環境為32位Windows7操作系統下的MatlabR2010a。以歸一化均方誤差(normalizedmeansquarederror,NMSE)和準確重構率(accuratereconstructionrate,ARR)作為衡量算法重構性能的指標。

NMSE與ARR的定義式[9]分別為

(8)

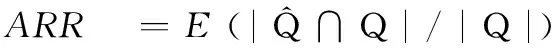
(9)

3.1利用BPMMP算法和BPMMPMMV算法重構合成信號的實驗

本節以隨機塊稀疏信號作為實驗對象。參數設置如下:原始信號中的非零值服從[0,1]上的均勻分布,信號長度N=500,MMV模型的信號個數n=10,信號觀測值的維數M根據采樣率設置,觀測矩陣A中的元素符合高斯分布N(0,1/N),且A的每一行均經過歸一化處理。合成信號的稀疏度為30,支撐隨機分布在5個集中的位置,每個位置支撐的個數是隨機的。原子塊的大小d=4,重疊原子數為2。實驗在不同采樣率下進行,每個采樣率下重復進行500次。這里以采樣率[0.1,0.2]區間為例展示實驗結果。

(1)BPMMP算法與MMP、SMP、BA*OMP算法的比較

圖2顯示了在不考慮噪聲影響的情況下,BPMMP算法與MMP、SMP和BA*OMP算法的NMSE值和ARR值的對比情況。

圖2　無噪聲時BPMMP算法與MMP、SMP和BA*OMP算法重構性能的比較　Fig.2　Reconstruction performance comparison of BPMMP with MMP, SMP and BA*OMP in the absence of noise

由圖2可見,在無噪聲影響的情況下,與MMP算法相比,BPMMP算法的NMSE值更低、ARR值更高。這說明,與MMP算法相比,BPMMP算法具有更高的重構性能,更適用于塊稀疏信號的重建。圖2還表明,BPMMP算法的重構性能優于同樣適用于重構塊稀疏信號的SMP算法,且當采樣率大于0.11之后,BPMMP算法的重構性能不低于BA*OMP算法。

以原子塊為單位進行路徑擴充以及剪枝操作的引入必然使得BPMMP算法的運行時間顯著低于MMP算法。表2顯示了在不考慮噪聲影響的情況下,在不同采樣率下,BPMMP算法的運行時間分別與BA*OMP算法和SMP算法運行時間的比值。由表2可見,在采樣率大于0.12之后,BPMMP算法的運算時間低于BA*OMP算法與SMP算法。

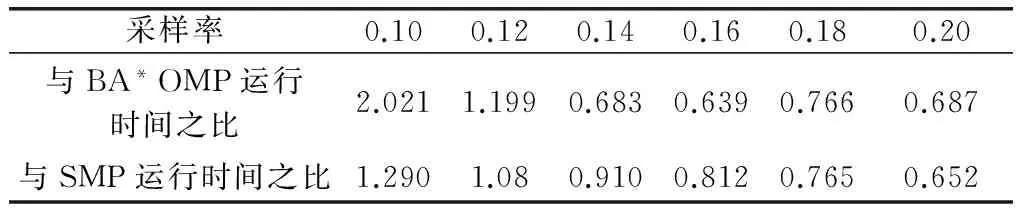
表2　無噪聲時BPMMP算法運行時間分別與BA*OMP算法和SMP算法運行時間的比值

(2) BPMMPMMV算法與BA*OMPMMV、SMP-MMV、SMP-GMMV和OMPMMV的比較

圖3、圖4分別顯示了在不考慮噪聲影響和當SNR=10 dB時在采樣率[0.1,0.2]范圍內BPMMPMMV、BA*OMPMMV、SMP-MMV、SMP-GMMV和OMPMMV 5種算法的NMSE值和ARR值的變化情況。由圖3、圖4可見,在無噪聲影響或當SNR=10 dB時,對于隨機合成的MMV模型塊稀疏信號,BPMMPMMV算法的聯合重構性能明顯優于OMPMMV算法與SMP-MMV算法;在采樣率超過0.12之后,BPMMPMMV算法的聯合重構性能高于SMP-GMMV算法;在采樣率超過0.11之后,BPMMPMMV算法的聯合重構性能不低于BA*OMPMMV算法。

圖3　無噪聲時5種算法重構性能的比較Fig.3　Performance comparison of five reconstruction algorithms in the absence of noise

在上述5種聯合重建算法中,BPMMPMMV算法和BA*OMPMMV算法的重建性能較高。下面在不考慮噪聲影響的情況下比較BPMMPMMV算法和BA*OMPMMV算法的資源消耗。實驗中發現,當NMSE值達到10-2時,BPMMPMMV和BA*OMPMMV需要的觀測值數量M分別為60和64;當NMSE值達到10-3時,BPMMPMMV和BA*OMPMMV需要的觀測值數量分別為64和70;當NMSE值達到10-30時,BPMMPMMV和BA*OMPMMV需要的觀測值數量分別為66和76。可見,當BPMMPMMV算法和BA*OMPMMV算法達到相同NMSE值時,前者比后者需要更少的觀測值。因此,與BA*OMPMMV算法相比,BPMMPMMV算法能夠降低數據采集與傳輸過程中的能量消耗,減少存儲空間占用,節約資源。

圖4　SNR=10 dB時5種算法重構性能的比較Fig.4　Performance comparison of five reconstruction algorithms when SNR=10 dB

表3、表4分別給出了在無噪聲影響和當SNR=10 dB時,BPMMPMMV算法運行時間分別與BA*OMPMMV、SMP-MMV、SMP-GMMV算法運行時間的比值。由表3、表4可見,在不考慮噪聲影響和當SNR=10 dB時,對于重構隨機合成的MMV模型塊稀疏信號,BPMMPMMV算法的運行時間明顯低于BA*OMPMMV、SMP-MMV和SMP-GMMV算法。

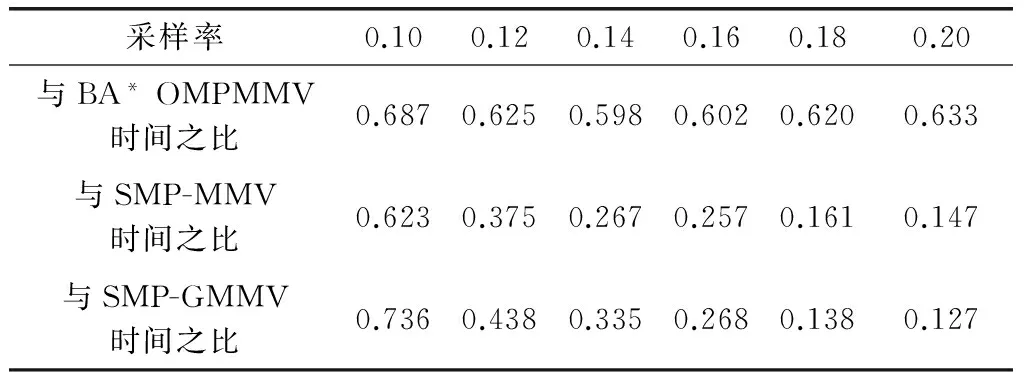
表3　無噪聲時BPMMPMMV分別與BA* OMPMMV、SMP-MMV、SMP-GMMV運行時間的比值

表4　SNR=10 dB時BPMMPMMV與BA*OMPMMV、SMP-MMV、SMP-GMMV運行時間的比值

3.2利用BPMMPMMV算法重構多傳感器實測溫度信號

本節采用Intel Berkeley Research Lab真實傳感器網絡的實測溫度值進行實驗。選取小空間范圍內的傳感器1、2、3、4、6、7、8、9、10和11這10個傳感器。將2004年3月1日到2004年3月7日內傳感器測得的溫度值每隔3.5 min采樣一個點,得到長度為2 048的溫度信號。選取sym8小波基。將觀測矩陣構造為元素符合高斯分布且每一行均經過歸一化處理的隨機矩陣。

分別在不考慮噪聲影響和在信噪比SNR=10 dB、15dB、20 dB的情況下,比較BPMMPMMV、BA*OMPMMV、SMP-MMV、SMP-GMMV和OMPMMV這5種算法的聯合重建性能。表5給出了當SNR=10 dB時,5種算法NMSE值的對比情況。表6給出了當SNR=10 dB時,BPMMPMMV算法運行時間分別與BA*OMPMMV、SMP-MMV和SMP-GMMV算法運行時間的比值。

表5　SNR=10 dB時5種算法NMSE值的對比

由表5可見,當SNR=10 dB時,對于重構實際WSN測得的溫度信號,適用于重構塊稀疏信號的BPMMPMMV、BA*OMPMMV、SMP-MMV和SMP-GMMV算法的聯合重構性能明顯優于OMPMMV算法。比較BPMMPMMV、BA*OMPMMV、SMP-MMV和SMP-GMMV 4種算法可見,BPMMPMMV算法的聯合重構性能優于BA*OMPMMV和SMP-MMV算法,而與SMP-GMMV算法基本相當。然而,SMP-GMMV算法采用的是GMMV模型,即對不同信號采用不同的觀測矩陣,因此會增加觀測矩陣存儲與傳輸的成本。

由表6可見,當SNR=10 dB時,對于重構實際WSN測得的溫度信號,BPMMPMMV算法的運行時間遠遠低于BA*OMPMMV、SMP-MMV和SMP-GMMV算法。在無噪聲影響、SNR=15dB、20 dB等情況下進行的實驗也得到了相同的結論。

表6　SNR=10 dB時BPMMPMMV分別與BA*OMPMMV、SMP-MMV和SMP-GMMV運行時間的比值

由上述實驗結果可見,從聯合重構性能與運行時間兩方面綜合考慮,與BA*OMPMMV、SMP-MMV、SMP-GMMV和OMPMMV算法相比,BPMMPMMV算法更適用于實現WSN小范圍內多傳感器采集信號的聯合重構。

4　結　論

本文針對MMP算法不能利用信號的塊稀疏結構且迭代次數較多時產生極大數據量的問題,提出了BPMMP算法,在獲得良好重建效果的基礎上,極大地降低了運行時間。進而,針對MMV問題進一步改進,提出了適用于在MMV模型下重構塊稀疏信號的BPMMPMMV算法。利用合成信號與Intel Berkeley Research Lab實際WSN測得的溫度信號進行的仿真實驗表明,BPMMPMMV算法具有優于BA*OMPMMV、SMP-MMV和OMPMMV算法的聯合重構性能,并且其運行時間顯著低于BA*OMPMMV、SMP-MMV和SMP-GMMV算法,更適用于WSN小范圍內多傳感器采集數據的聯合重構。

本文設計的BPMMP算法在固定的迭代層數之后,從每層搜索出的候選路徑集中去除固定比例的路徑。如何在迭代過程中適時地對搜索樹進行適度修剪是一個需要進一步研究的問題。

[1] Baron D, Duarte M F, Sarvotham S, et al. An information-theoretic approach to distributed compressed sensing[C]∥Proc.ofthe43rdAllertonConferenceonCommunication,Control,andComputing, 2005: 814-825.

[2] Youness N, Hassan K. Energy preservation in large-scale wireless sensor network utilizing distributed compressive sensing[C]∥Proc.ofthe10thIEEEInternationalConferenceonWirelessandMobileComputing,NetworkingandCommunications, 2014: 251-256.

[3] Chen J, Huo X. Theoretical results on sparse representations of multiple measurement vectors[J].IEEETrans.onSignalProcessing, 2006, 54(12): 4634-4643.

[4] Davies M E, Eldar Y C. Rank awareness in joint sparse recovery[J].IEEETrans.onInformationTheory, 2012, 58(2): 1135-1146.

[5] Eldar Y C, Mishali M. Block-sparsity and sampling over a union of subspaces[C]∥Proc.ofthe16thInternationalConferenceonDigitalSignalProcessing, 2009: 1-8.

[6] Eldar Y C, Kuppinger P, Bolcskei H. Block-sparse signals: uncertainty relations and efficient recovery[J].IEEETrans.onSignalProcessing, 2010, 58(6): 3042-3054.

[7] Chen P, Wang C, Meng C. Block compressive sampling matching pursuit based on restricted isometry property[J].SystemsEngineeringandElectronics, 2015, 37(2): 239-245. (陳鵬, 王成, 孟晨. 基于約束等距的塊稀疏壓縮采樣匹配追蹤算法[J].系統工程與電子技術, 2015, 37(2): 239-245.)

[8] Tian P W, Kang R Z, Yu H Y. Compressive sampling of non-uniform block sparse signals and the blind recovery algorithm[J].JournalofElectronics&InformationTechnology, 2013, 35(2): 445-450. (田鵬武, 康榮宗, 于宏毅. 非均勻塊稀疏信號的壓縮采樣與盲重構算法[J].電子與信息學報, 2013, 35(2): 445-450.)

[9] Lian Q S, Liu F, Chen S Z. A joint reconstruction algorithm for multiple sensor data based on block A*orthogonal matching pursuit[J].JournalofElectronics&InformationTechnology, 2013, 35(3): 721-727. (練秋生, 劉芳, 陳書貞. 基于塊 A*正交匹配追蹤的多傳感器數據聯合重構算法[J].電子與信息學報, 2013, 35(3): 721-727.)

[10] Ganesh A, Zhou Z. Separation of subspace-sparse signal: algorithms and conditions[C]∥Proc.oftheIEEEInternationalConferenceonAcoustics,Speech,andSignalProcessing, 2009: 3141-3144.

[11] Joshi A, Kannu P A. On recovery of block sparse signals from multiple measurements[C]∥Proc.oftheIEEEInternationalConferenceonAcoustics,Speech,andSignalProcessing, 2014: 7163-7167.

[12] Kwon S, Wang J, Shim B. Multipath matching pursuit[J].IEEETrans.onInformationTheory, 2014, 60(5): 2896-3001.

[13] Bodik P, Hong W, Guestrinc, et al. Intel Berkeley Lab WSN[EB/OL].[2015-6-28]. http:∥db.csail.mit.edu/labdata/labdata.html.

[14] Ding J, Chen L, Gu Y. Performance of orthogonal matching pursuit for multiple measurement vectors[C]∥Proc.oftheIEEEChinaSummitandInternationalConferenceonSignalandInformationProcessing, 2013: 67-71.

[15] Kim J M, Lee O K, Ye J C. Compressive MUSIC: revisiting the link between compressive sensing and array signal processing[J].IEEETrans.onInformationTheory, 2012, 58(1): 278-301.

[16] Gishkori S, Leus G. Compressed sensing for block-sparse smooth signals[C]∥Proc.oftheIEEEInternationalConferenceonAcoustic,SpeechandSignalProcessing, 2014: 4166-4170.

[17] Wimalajeewa T, Eldar Y C, Varshney P K. Subspace recovery from structured union of subspaces[J].IEEETrans.onInformationTheory, 2015, 61(4): 2101-2114.

[18] Wang Y G, Liu Z, Jiang W L, et al. Block sparse signal recovery with synthesized multitask compressive sensing[C]∥Proc.oftheIEEEInternationalConferenceonAcoustic,SpeechandSignalProcessing, 2014: 1030-1034.

Joint multi-signal reconstruction based on block pruning multipath matching pursuit

SI Jing-jing, HOU Xiao-lan, CHENG Yin-bo

(SchoolofInformationScienceandTechnology,YanshanUniversity,Qinhuangdao066004,China)

Considering the disadvantages of ignoring signal’s structured sparsity and the high complexity in high iterative layers in multipath matching pursuit (MMP), the block pruning multipath matching pursuit (BPMMP) is proposed to reconstruct the block-sparse signal. In this algorithm, an atomic block serves as a node in the path expansion, and branch pruning operation is introduced after a certain number of iterations. Thus, BPMMP reduces the data processing cost greatly. Moreover, for multiple measurement vector (MMV) problem, BPMMP for MMV (BPMMPMMV) is proposed. It can achieve joint signal reconstruction for multiple sensors within a small range in the wireless sensor network. Experimental results show that BPMMP outperforms MMP on the reconstruction performance, and BPMMPMMV achieves higher joint reconstruction performance than block A*orthogonal matching pursuit for MMV, subspace matching pursuit for MMV and orthogonal matching pursuit for MMV.

distributed compressed sensing (DCS); multiple measurement vector (MMV); block sparsity; multipath matching pursuit (MMP)

2015-09-23；

2016-02-21；網絡優先出版日期：2016-07-05。

國家自然科學基金(61471313，61303128)；河北省自然科學基金(F2014203183)；河北省高等學校科學技術研究項目(Q2012087);燕山大學青年教師自主研究計劃(13LGB015)資助課題

TN 919.8

A

10.3969/j.issn.1001-506X.2016.09.05

司菁菁(1980-),女,副教授,博士,主要研究方向為壓縮感知、網絡編碼。

E-mail:sjj@ysu.edu.edn

候肖蘭(1988-),女,碩士研究生,主要研究方向為分布式壓縮感知。

E-mail:houxiaolanqian@163.com

程銀波(1978-),男,講師,博士,主要研究方向為分布式計算。

E-mail:cyb@ysu.edu.cn

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160705.1722.004.html