立方體衛星制動帆裝置離軌時間分析

梁振華　曾玉堂　張　翔　莫乾坤　于永軍　廖文和（南京理工大學機械工程學院，南京 210094）

立方體衛星制動帆裝置離軌時間分析

梁振華曾玉堂張翔莫乾坤于永軍廖文和
（南京理工大學機械工程學院，南京 210094）

為了避免立方體衛星（CubeSat）失效后成為空間碎片，在立方體衛星壽命末期應采用低成本制動帆裝置使其快速脫離軌道，從而減少對低地球軌道（LEO）航天器碰撞和損壞的威脅。文章建立了立方體衛星離軌的數學模型，得到立方體衛星離軌時間的影響因素分別為立方體衛星面質比、軌道高度和發射日期。應用實例仿真分析上述3種影響因素對離軌時間的影響，結果表明：隨著立方體衛星面質比的增加，離軌時間不斷減少；軌道高度越高，離軌時間越長；發射日期不同，離軌時間也存在較大的差異，在太陽活動峰年時離軌時間短，在太陽活動低年時離軌時間長。根據分析結果，對于3U立方體衛星而言，制動帆面積可設計為4 m2。

立方體衛星；制動帆裝置；離軌時間；面質比；軌道高度；發射日期

1　引言

從20世紀60年代以來，空間碎片的數量迅速增長，并且主要集中在距離地面1000km以下的低地球軌道（LEO）。隨著空間碎片數量的不斷積累，碰撞的風險也不斷增加，碰撞產生的碎片又會繼續與其他空間物體碰撞產生新的碎片，如果不及時采取措施，這種潛在的多米諾效應將導致空間環境持續惡化［1］。目前，一些在軌航天器已經受到空間碎片的威脅，最明顯的例子是2009年廢棄的蘇聯宇宙-2251（Kosmos-2251）衛星與美國銥-33（Iridium-33）衛星發生碰撞［2］。2007年，機構間空間碎片協調委員會（IADC）出版了《空間碎片緩解指南》，建議航天器在完成任務后25年內或者入軌后30年內應脫離軌道［3］。因此，研究航天器離軌技術具有非常重要的意義。

立方體衛星（CubeSat）是一種體積和形狀標準化的微納衛星，由于其易于實現標準化、模塊化，研制周期短，經濟成本低，越來越受到國內外的重視［4］。立方體衛星發射數量的增多，對空間環境的影響也越來越顯著，如果沒有一個可靠的離軌技術，未來立方體衛星的發射將會受到一定的影響。近年來，國外許多高校及研究所都積極投身于立方體衛星離軌技術的研究，典型的離軌方式包括充氣球、電動力系繩和制動帆。充氣球利用太陽光壓及氣動阻力，實現10000km高度以下的中地球軌道（MEO）立方體衛星離軌，應用范圍廣，但是須要攜帶氣體增壓裝置，給衛星發射和長時間在軌飛行帶來了一定的安全隱患，并且高壓氣體不可避免地引起氣體泄漏也會縮短使用壽命［5-8］。電動力系繩離軌速度快，但是其展開后可達到數十米甚至數千米，會增加LEO立方體衛星任務的風險。此外，電動力系繩是利用高速運動的導電繩索切割地磁場磁力線，從而產生垂直于系繩和當地磁場方向的作用力，對于一些極軌道衛星而言，該裝置存在一定的局限性［9-10］。制動帆主要通過提高衛星在軌飛行過程中所受到的大氣阻力，從而加速衛星離軌。在制動帆裝置工作過程中不需要衛星進行主動控制，可以依靠裝置自身所儲存的機械能來展開。由于制動帆裝置質量小，機構簡單，成本低，適用于快速響應、任務周期短的LEO微納衛星，因而受到了國內的廣泛關注。

薩瑞大學研制的“立方帆”（Cubesail），其展開面積可達25m2，安裝在一顆3U（質量約3kg）立方體衛星上。在衛星任務初期，控制衛星的姿態使帆面對準太陽，帆面受到太陽光子的連續撞擊后能獲得一定的推力，可實現衛星軌道傾角的微小變化。在衛星任務末期，通過控制衛星的姿態，使帆面垂直于速度方向，增加衛星所受到的大氣阻力，從而實現衛星快速脫離軌道［11］。多倫多大學的加拿大先進航天實驗-7（Can X-7）立方體衛星，主要驗證了該校所研制的制動帆裝置，該裝置主要由4個相同的展開帆單元組成，每個單元可展開成一個約1 m2的梯形帆，可以實現3種質量大小不同的LEO衛星在25年內脫離軌道［12］。此外，格拉斯哥大學所研制的“空氣動力學壽命末期離軌系統”（AEOLDOS）制動帆裝置，其展開面積僅為1m2，但可實現650 km軌道高度以下的立方體衛星在25年內脫離軌道［13］。NASA的納型帆-D（NanoSail-D）制動帆，帆面積為10m2，將其安裝在一顆3U立方體衛星上，實現了離軌演示驗證，這是迄今為止唯一報道過已得到演示驗證的制動帆裝置，該裝置占據了星內2U的空間［14］。目前，制動帆裝置主要基于特定任務的立方體衛星設計，應用范圍較小，并且缺乏較為系統的立方體衛星離軌時間理論分析。本文主要針對制動帆裝置設計過程中的關鍵技術，開展了立方體衛星離軌時間的理論研究，分析了立方體衛星離軌時間的影響因素，可為制動帆的設計及制造提供一定的參考。

2　立方體衛星離軌的數學模型

在數學模型分析過程中，忽略大氣隨地球的旋轉，并且認為大氣只產生相對于衛星速度方向相反的阻力，而沒有升力。

立方體衛星在軌完成相關任務后至其脫離軌道的這段時間，即為離軌時間，計算公式為［15］

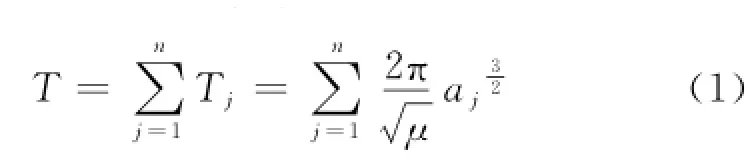
式中:μ為地球引力常數；n為立方體衛星離軌過程中繞地球的圈數；Tj為衛星第j圈的軌道周期；aj為立方體衛星第j圈的軌道半長軸平均值。

從式（1）可知，立方體衛星離軌時間主要取決于軌道半長軸a和繞地球的圈數n。

立方體衛星在軌時主要受到大氣阻力攝動影響，從而導致軌道高度逐漸降低，其運動方程為

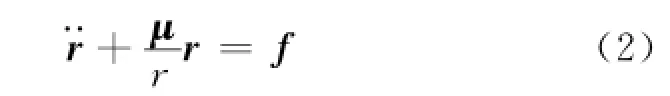
式中:r為衛星地心距；f為大氣阻力攝動加速度。

立方體衛星的軌道坐標系定義為:坐標原點為衛星質心o，oz軸在軌道平面內，由衛星質心指向地心O，ox軸在軌道平面內垂直于oz軸，指向衛星速度方向，oy軸滿足右手坐標系。將f在立方體衛星軌道坐標系oxyz中分解，如圖1所示，其中fx，fy，fz分別為立方體衛星在橫向、法向以及徑向上所受到的大氣阻力。

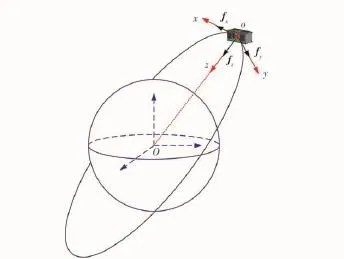
圖1　立方體衛星所受到的大氣阻力Fig.1　Atmospheric drag of CubeSat

大氣阻力對立方體衛星僅產生徑向和橫向攝動加速度，在垂直于軌道平面的法向加速度為0，因此進一步簡化式（2），得到立方體衛星受大氣阻力影響時軌道要素的變化［15］。

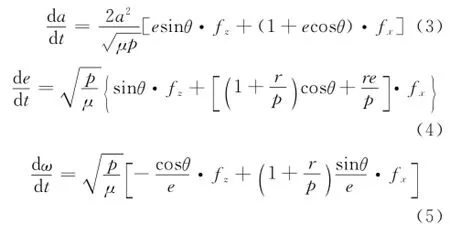
式中:e為軌道偏心率；θ為真近角；ω為近地點幅角；半正通徑P=a（1—e2）。

通過求解差分方程式（3）～（5），可以得到軌道根數a，e，ω的變化率，并進一步計算出衛星的軌道周期，從而得出立方體衛星的離軌時間。

半長軸的變化率主要受大氣阻力攝動影響，通過在立方體衛星上安裝制動帆裝置，增加衛星在運行速度方向的阻力，從而加快立方體衛星脫離軌道。立方體衛星在軌受到大氣阻力攝動加速度表達式為［16］

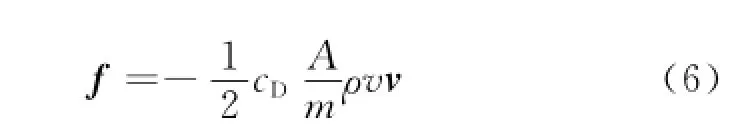
式中:cD為阻力系數，一般取2.2；A為衛星阻力面積，一般等于迎風面積；m為衛星質量；ρ為大氣密度；v為立方體衛星相對大氣的運動速度。

由式（6）可以看出，立方體衛星受到的大氣阻力攝動加速度主要與衛星面質比（阻力面積與質量的比值）、衛星相對大氣的運動速度、大氣密度有關。在質量一定的情況下，衛星面質比主要由衛星阻力面積決定，安裝制動帆裝置后，帆面積越大，所受的阻力也越大。立方體衛星運動速度則由軌道高度決定，軌道高度越低，立方體衛星相對大氣的運動速度越快。大氣密度除了隨軌道高度的上升呈指數下降外，還與太陽活動有關。太陽活動通常用10.7cm射電流量F10.7來表征，F10.7存在27天左右的短周期變化和11年左右的長周期變化，而后者振幅的變化可達3～4倍，引起大氣密度的變化將達40倍。此外，太陽在活動周期內所產生的太陽輻射、太陽風以及磁場的波動都會對立方體衛星的離軌時間產生影響［16］，因此立方體衛星發射日期的不同對離軌時間也會產生一定的影響。

下面本文將通過實例分析立方體衛星的離軌時間與衛星面質比、軌道高度、發射日期的關系。

3　仿真分析

仿真過程中，主要參數設置見表1，選擇高精度軌道外推模型（HPOP）［17］，其他參數均為軟件默認設置。本文設置立方體衛星在軌道高度降至120 km時即為已經脫離軌道，因為在此軌道高度下，任何物體都會在較短時間內衰減至地球大氣層燒毀，除非獲得一定的推力使其重返軌道［17］。當軌道高度高于1000km時，大氣密度較低，制動帆裝置的應用范圍受限［18］，因此在分析過程中，軌道高度最高設定為1000km。

表1　主要參數Table1　Main parameters

3.1立方體衛星面質比和軌道高度的影響

常規狀態下，設置制動帆裝置后，通過調整衛星的姿態，使制動帆垂直于衛星速度方向，從而提高立方體衛星的面質比。隨著立方體衛星的不斷發展，星內功能密度也越來越高，立方體衛星的質量也不斷增加，部分3U立方體衛星的質量甚至達到了4.5kg［19］。此外，國外已經著手研制6U的立方體衛星［20］，使立方體衛星的應用不斷得到拓展，因此需要的制動帆面積也不斷提高。本節選擇0.5m2/kg，1.0m2/kg，1.5m2/kg，2.0m2/kg，2.5m2/kg的面質比，400～1000 km的太陽同步軌道，分析立方體衛星在不同面質比時的離軌時間，如圖2所示。

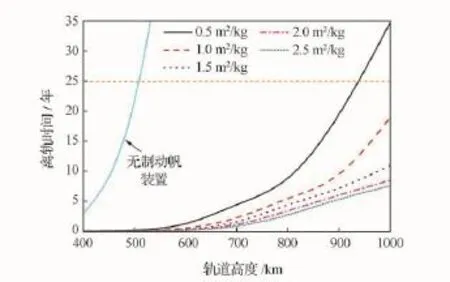
圖2　立方體衛星面質比與離軌時間的關系Fig.2　Relationship between area-mass ratio and de-orbiting time

由圖2可知:①在軌道高度低于500km時，由于大氣阻力較大，在不設置制動帆裝置時，立方體衛星也能夠在25年內脫離軌道；安裝制動帆裝置后，可以顯著降低離軌時間，并且幾種面質比下的立方體衛星離軌時間相差較小。②隨著軌道高度不斷提高，當不設置制動帆裝置時，立方體衛星的離軌時間迅速增加，遠遠高于IADC規定的離軌時間；安裝制動帆裝置后，面質比越大，立方體衛星離軌時間越短。在立方體衛星面質比一定時，離軌時間隨軌道高度的提高而增加，當達到一定的軌道高度時，一定面質比下的制動帆便不能滿足IADC規定的離軌要求，因此要適當增大制動帆的面積來增加面質比。③在軌道高度低于900km時，5種面質比下的立方體衛星均滿足離軌要求；繼續提高軌道高度，0.5m2/kg的立方體衛星便不能在25年內脫離軌道；此外，2.0m2/kg和2.5m2/kg面質比的立方體衛星離軌時間最短，并且二者相差較小。因此，對于立方體衛星而言，當衛星質量一定時，通過增加制動帆的面積提高面質比，可以有效縮短離軌時間，然而，過度地增大制動帆面積會占據星內較大的空間，質量一定的情況下，應充分考慮立方體衛星所處的軌道高度，設計出合理的制動帆面積。

從圖2不難看出，1000km軌道高度下的立方體衛星，設置面質比為1.0m2/kg，即可在25年內脫離軌道。對于常規3U立方體衛星而言，其質量約為3kg，此時所需要的制動帆面積應不低于3m2。

3.2發射日期的影響

本節主要仿真在未來30年內不同發射日期對立方體衛星離軌時間的影響，分析結果如圖3所示，立方體衛星的質量為3kg（3U）。圖3（a）為立方體衛星的帆面積為4m2時，5種不同軌道高度下離軌時間與發射日期的關系；圖3（b）為立方體衛星的軌道高度為800km時，4種不同帆面積的離軌時間與發射日期的關系。

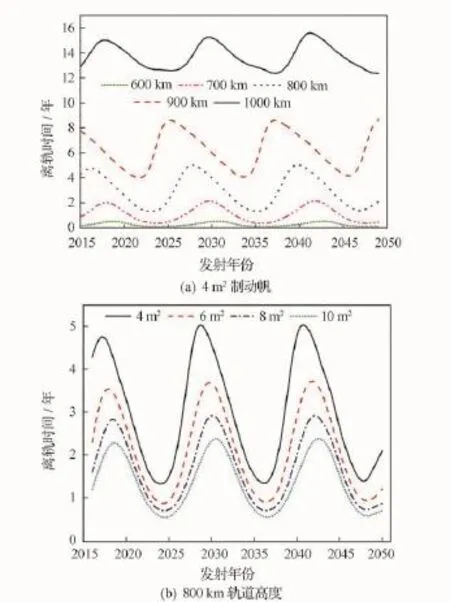
圖3　離軌時間與發射日期的關系Fig.3　Relationship between de-orbiting time and launch date

由圖3可知:①在軌道高度和制動帆面積一定的情況下，立方體衛星的離軌時間遵循太陽活動周期呈波浪形曲線變化。在太陽活動峰年時，離軌時間短；在太陽活動低年時，離軌時間長。②當制動帆面積一定時，軌道高度越高，立方體衛星的離軌時間越長，離軌時間受發射日期的影響波動也越明顯。在軌道高度為900km時，最大值與最小值相差可達4.9年，而當軌道高度降至600km時，二者相差僅約為0.4年（160天）。③低于1000km的4種軌道高度上，立方體衛星的離軌時間峰值與谷值所處的年份基本一致；而當軌道高度提高至1000km時，不僅立方體衛星的離軌時間遠遠高于其他4種軌道高度，其離軌時間的峰值與谷值所處的年份與其他4種軌道高度也存在較大的差異。④在軌道高度一定時，制動帆面積越大，離軌時間越短，受發射日期影響的波動也越小。在制動帆面積為4m2時，最大值與最小值相差約3.8年（1387天），而當制動帆面積為10m2時，二者相差約為1.5年（548天）。考慮到發射日期對立方體衛星離軌所產生的影響，當立方體衛星質量較大并且軌道高度較高時，由于離軌時間長，受發射日期的影響較大，在不影響星內其他有效載荷的情況下，應選擇面積較大的制動帆裝置；當立方體衛星質量較小、軌道高度較低時，由于離軌時間短，因此可以忽略發射日期對立方體衛星離軌時間的影響。從圖3還可看出，在軌道高度低于1000km時，4m2制動帆基本可以滿足3U立方體衛星的離軌要求，即使在軌道高度達到1000km時，雖然離軌時間較長，變化幅度較大，但是均能在IADC規定的時間范圍內脫離軌道。

4　結論

常規立方體衛星的設計壽命一般較短，其失效后逗留在太空會對其他正常運行的航天器產生很大的威脅。為了使立方體衛星能以低成本快速地脫離軌道，本文主要分析了立方體衛星面質比、軌道高度、發射日期對立方體衛星離軌時間的影響。根據上文的仿真分析結果，得到結論如下。

（1）衛星面質比越大，立方體衛星離軌時間越短。

（2）軌道高度越高，立方體衛星離軌時間越長；通過增大制動帆面積來提高衛星面質比，可以有效縮短立方體衛星的離軌時間。

（3）隨著立方體衛星發射日期的不同，離軌時間存在較大的差異。在太陽活動峰年時離軌時間短，在太陽活動低年時離軌時間長，并且立方體衛星離軌時間越長，受發射日期的影響也越明顯。因此，在立方體衛星離軌時間較長時，為了減少發射日期所產生的影響，應選擇面積較大的制動帆裝置；當立方體衛星離軌時間較短時，則可以忽略發射日期對立方體衛星離軌時間的影響。

（4）當軌道高度低于1000km時，對于3U立方體衛星而言，4m2制動帆基本可以滿足其離軌要求。

由于制動帆面積越大，裝置在星內所占據的空間也越大，因而在設計制動帆時，應充分結合立方體衛星的質量、所在的軌道高度以及發射日期，選擇合理的制動帆大小，從而使立方體衛星能夠在較短的時間內脫離軌道，以有效避免立方體衛星廢棄后與其他在軌航天器發生碰撞。

（References）

［1］Bonnal C，Ruault J M，Desjean M C.Active debris removal:recent progress and current trends［J］.Acta Astronautica，2013（85）:51-60

［2］Ting Wang.Analysis of debris from the collision of the Cosmos 2251 and the Iridium 33 satellites［J］.Science& Global Security，2010，18:87-11

［3］Reintsema D，Thaeter J，Rathke A，et al.DEOS—the German robotics approach to secure and de-orbit malfunctioned satellites from low earth orbits［C］//Proceedings of International Symposium on Artificial Intelligence，Robotics and Automation in Space（i-SAIRAS）. Cologne:German Aerospace Center，2010:244-251

［4］Bouwmeester J，Guo J.Survey of worldwide pico-and nanosatellite missions，distributions and subsystem technology［J］.Acta Astronautica，2010（67）:854-862

［5］Nock K，Gates K，Aaron K，et al.Gossamer Orbit Lowering Device（GOLD）for safe and efficient de-orbit ［C］//Proceedings of AIAA/AAS Astrodynamics Specialist Conference.Washington D.C.:AIAA，2010: 1-11

［6］Lcking C，Colombo C，Mcinnes C.A passive de-orbiting strategy for high altitude CubeSat missions using a deployable reflective balloon［C］//Proceedings of the 8th IAA Symposium on Small Satellites.Stockholm: IAA，2011:1-8

［7］Hawkins Jr R A.Analysis of an inflatable gossamer device to efficiently de-orbit CubeSats［D］.San Luis Obispo:California Polytechnic State University，2013

［8］Charlotte L，Camilla C，Colin R，et al.A passive satellite deorbiting strategy for medium earth orbit using solar radiation pressure and the J2 effect［J］.Acta Astronautica，2012（77）:197-206

［9］劉文佳.電動力纜繩離軌特性研究［D］.哈爾濱:哈爾濱工業大學，2006 Liu Wenjia.Deorbiting characteristic research on electrodynamic tether［D］.Harbin:Harbin Institute of Technology，2006（in Chinese）

［10］Kentaro Iki，Satomi Kawamoto，Yoshiki Morino.Experiments and numerical simulations of an electrodynamic tether deployment from a spool-type reel using thrusters［J］.Acta Astronautica，2014（94）:318-327

［11］Lappas V，Adeli N，Visagie L，et al.CubeSail:a low cost CubeSat based solar sail demonstration mission ［J］.Advances in Space Research，2011，48（11）:890-901

［12］Jesse Hiemstra.Mechanical design and development of a modular drag sail for the Can X-7 nanosatellite mission［D］.Toronto:University of Toronto，2014

［13］Harkness P，Mcrobb M，Ltzkendorf P，et al.Develop-ment status of AEOLDOS—a deorbit module for small satellites［J］.Advances in Space Research，2014（54）: 82-91

［14］Malcolm Macdonald.Advances in solar sailing［M］. Berlin:Springer，2014

［15］趙鈞.航天器軌道動力學［M］.哈爾濱:哈爾濱工業大學出版社，2011 Zhao Jun.Orbital dynamics of spacecraft［M］.Harbin:Harbin Institute of Technology Press，2011（in Chinese）

［16］Thomas Mc Grath.Sail，deployment，and imaging technology for a nanosatellite deorbit system demonstration on CanX-7［D］.Toronto:University of Toronto，2014

［17］溫生林，閆野，易騰.超低軌道衛星攝動特性分析及軌道維持方法［J］.國防科技大學學報，2015，37（2）:128-134 Wen Shenglin，Yan Ye，Yi Teng.Analyzing perturpation characteristics and orbital maintenance strategy for super low altitude satellite［J］.Journal of National University of Defence Technology，2015，37（2）:128-134（in Chinese）

［18］Grant B，Jesse H，Thomas S，et al.The Can X-7 drag sail demonstration mission:enabling environmental stewardship for nano-and microsatellites［C］//Proceedings of the 27th Annual AIAA/USU Conference on Small Satellites.Washington D.C.:AIAA，2013: 1-10

［19］Kirk W，Pascale E，Antonio J，et al.Cubesats:costeffective science and technology platforms for emerging and developing nations［J］.Advances in Space Research，2011（47）:663-684

［20］Sharmila P，Shannon B，Pekka K，et al.A 6U CubeSat constellation for atmospheric temperature and humidity sounding［C］//Proceedings of the 27th Annual AIAA/USU Conference on Small Satellites.Washington D.C.:AIAA，2013:1-5

（編輯：夏光）

De-orbiting Time Analysis on Drag Sail Device of CubeSat

LIANG Zhenhua ZENG Yutang ZHANG Xiang MO Qiankun YU Yongjun LIAO Wenhe
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China）

To avoid a non-functional CubeSat becoming space debris，it is necessary to use a lowcost drag sail device as an end-of-life disposal which makes the CubeSat deorbit quickly and decreases the threat of collisions and damages to other spacecraft.A CubeSat de-orbiting mathematical model is established，and the factors influencing de-orbiting time are obtained such as areamass radio，orbit altitude and launch date.Some examples are used to analyze these factors，and the simulation results show that the area-mass ratio of CubeSat has high influence on the de-orbiting time.The greater area-mass ratio is，the shorter de-orbiting time is.Also，the de-orbiting time increases as the orbit altitude is increasing.What's more，the de-orbiting time of a CubeSat can vary depending on launch date that high solar activity gives lower de-orbiting time and low solar activity gives longer de-orbiting time.According to the results of the analysis，a drag sail device with a deployed areas of 4m2is designed for a 3U CubeSat.

CubeSat；drag sail device；de-orbiting time；area-mass radio；orbit altitude；launch date

V412.4

A

10.3969/j.issn.1673-8748.2016.03.004

2015-11-09；

2016-04-11

江蘇省普通高校研究生科研創新計劃項目（KYLX15_0343）

梁振華，男，博士研究生，研究方向為微小衛星軌道機動及離軌技術。Email：liangzh2014@126.com。