各向異性介質GPR非結構化網格有限元正演

石明，馮德山王洪華，戴前偉

（1. 中南大學 地球科學與信息物理學院，湖南 長沙，410083；2. 貴州省有色金屬和核工業地質勘查局物化探總隊，貴州 都勻，558004；3. 桂林理工大學 地球科學學院，廣西 桂林，541004）

各向異性介質GPR非結構化網格有限元正演

石明1，2，馮德山1，王洪華3，戴前偉1

（1. 中南大學 地球科學與信息物理學院，湖南 長沙，410083；2. 貴州省有色金屬和核工業地質勘查局物化探總隊，貴州 都勻，558004；3. 桂林理工大學 地球科學學院，廣西 桂林，541004）

為了更準確地認識電磁波在各向異性介質中的傳播特征，從麥克斯韋方程組出發，推導電磁場在單斜各向異性介質中的波動方程。采用 Delaunay 非結構化網格有限元法進行空間域離散，采用中心差分公式進行時間域離散，導出單斜各向異性介質中GPR時空域有限元方程。在此基礎上，建立各向異性介質GPR非結構化網格有限元正演算法。利用以上算法編制的程序對均勻各向異性介質模型進行正演計算，并與解析解對比，驗證該算法的正確性和有效性；對均勻各向異性介質模型和圓形異常體模型進行計算，并與背景介質為各向同性介質的計算結果進行對比。研究結果表明：與FDTD計算結果對比，非結構化網格有限元法的擬合誤差更小，精度更高；電磁波傳播受介質各向異性的影響，波前面呈橢圓狀向外擴散傳播，其能量衰減較慢；與各向同性介質中圓形異常體反射波相比，各向異性介質的圓形異常體反射波的曲率、能量和雙程走時，受不同方向上電磁波速度影響會發生顯著變化。

各向異性介質；非結構化網格有限單元法；探地雷達；正演模擬

探地雷達（ground penetrating radar，GPR）作為一種重要的淺部地球物理勘探手段被廣泛應用于工程勘察［1-2］、無損檢測［3］等眾多領域，具有廣闊的應用前景［4］。目前，GPR實測數據的解釋主要依賴各向同性介質的電磁波傳播理論，然而，隨著GPR應用領域的擴大，各向異性介質如冰川［5］、結晶體［6］、含水巖石、構造裂隙等已成為探測對象，與電磁波在各向同性介質中的傳播規律相比，電磁波在各向異性介質中傳播會發生畸變和衰減，因此，研究電磁波在各向異性介質中的傳播和異常體回波特征對提高 GPR實測數據的解釋精度有重要意義。GPR正演模擬是研究電磁波在各向異性介質中傳播規律的有效手段。在眾多的GPR正演算法中，時域有限差分法（finite difference time domain， FDTD）因其發展成熟和理論簡單而被廣泛應用。劉四新等［7-10］對FDTD算法在GPR正演中的應用進行了深入研究。但FDTD要求地電模型被剖分成如正方形、立方體等規則的單元，這嚴重制約著其在復雜介質模型的應用［11］。與FDTD相比，有限元法（finite element method，FEM）可以利用非結構化網格更精確的離散復雜介質模型［12］，在電磁波場梯度大的區域采用較密的網格，而在電磁波場變化平穩的區域采用較疏的網格。因此，采用較少的網格就可以構建復雜地質結構，具有更高的計算效率和模擬精度［13］。在目前的GPR正演模擬研究中，地下介質大都被假定為各向同性，人們對各向異性介質的GPR正演模擬研究較少，且大都采用FDTD算法［14-16］。為了更好地模擬電磁波在各向異性介質中的傳播規律，本文作者應用非結構化網格有限元法對各向異性介質中的電磁波傳播規律進行研究。通過對均勻各向同性介質模型、均勻各向異性模型、圓形異常體各向異性介質模型進行計算，并與各向同性介質的正演模擬結果進行對比，總結電磁波和異常體回波在各向異性介質中的傳播特征。

1 TM模式和TE模式的電磁波理論

根據電磁波理論，頻率域各向異性介質中的麥克斯韋方程可表示為

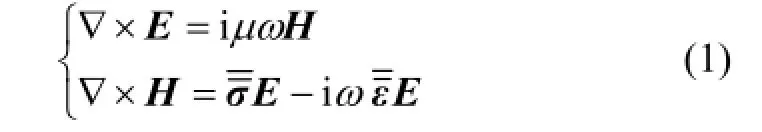
式中： εjj和σjj（j=xx，yy和zz）分別為j方向上的介電常數和電導率 。考慮二維情況，各向異性介質的主軸方向為z方向，將式（2）代入式（1），按照TE模式和TM模式分解為2組獨立的方程組。

1） TM模式：

2） TE模式：

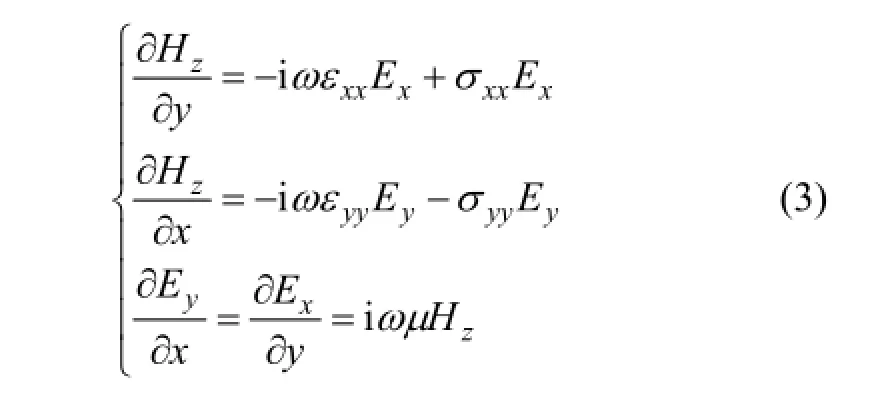
從式（3）可以看出：各向異性介質中TM模式滿足的方程與介電常數為 εzz和電導率為σzz的各向同性滿足的方程完全相同，而各向異性介質的 TE模式方程組與各向同性介質有較大的差別。將 TE模式方程中的前2式的Ex和Ey表達式代入第3式，經整理可得

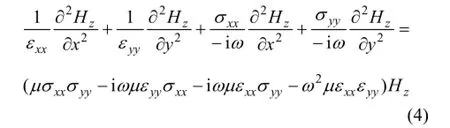
將式（4）兩邊同除以εμεyyxx，代入磁激勵源 Sh，并轉化到時間域可得

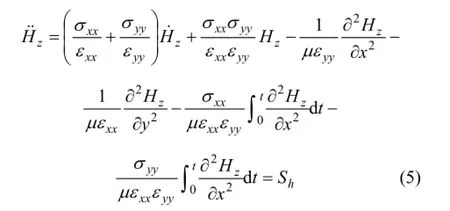
其中：Hz和Hz分別為Hz對時間的一次和二次導數。式（5）即為 TE模式下各向異性介質中的磁場波動方程。

2 各向異性介質的 GPR有限元正演模擬算法

求解 GPR波動方程的實質是應用伽略金有限單元法，結合初始、邊界條件，推導相應的有限元方程［17］。這里采用非結構化 Delaunay 網格［18］對計算區域進行剖分，如圖1所示。非結構化網格可在激勵源點附近與接收點附近采用密網格，而在大部分均勻介質區域采用疏網格剖分，因此，較少的網格數便可精確剖分復雜介質模型。根據有限單元法理論，三角單元內的磁場可用該單元上3個節點上的磁場表示為

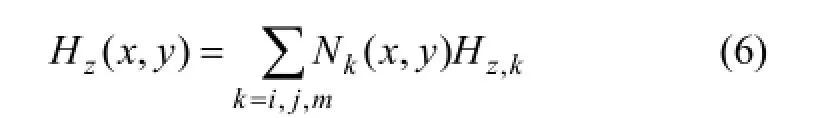
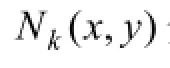
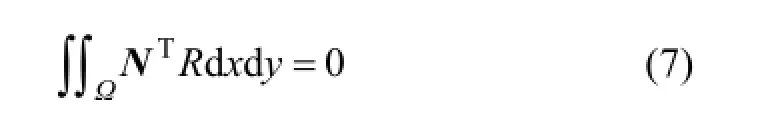
式中：R為方程（7）的殘差；?為計算區域面積；N為形函數向量。將式（5）和（6）代入式（7），可得

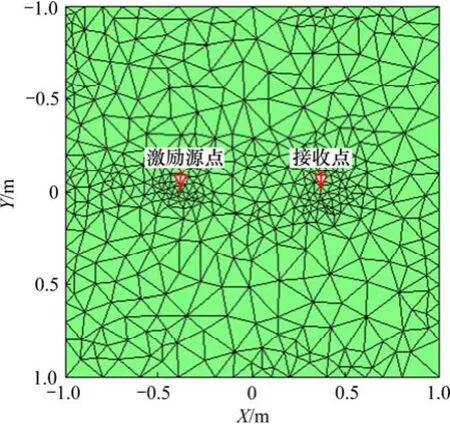
圖1 網格剖分及節點編號示意圖Fig.1 Sketch map of mesh division and point number

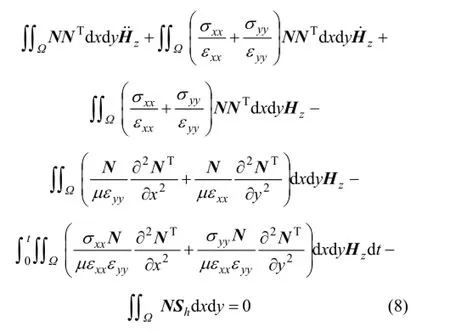
式（8）左邊第1項：

式（8）左邊第2項：

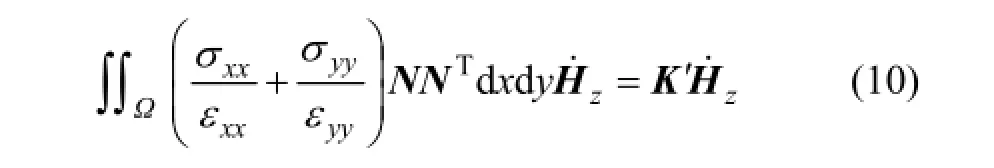
式（8）左邊第3項：

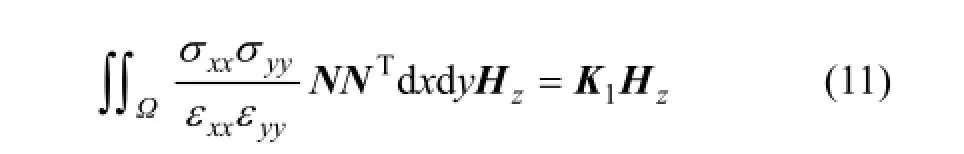
根據高斯定理，式（8）左邊第4項可寫為

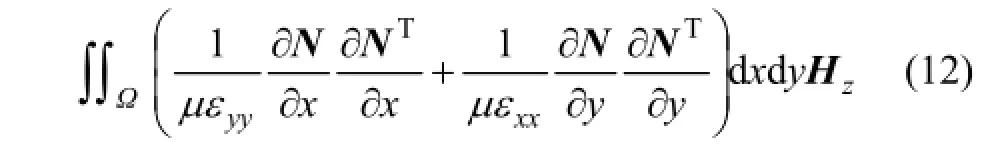
由電磁場理論可知，GPR波在模型邊界上向外傳播應該滿足

其中：k為電磁波在介質中傳播的波數；r為天線位置到邊界上任一點的距離。對式（14）兩邊對 r求導，可得

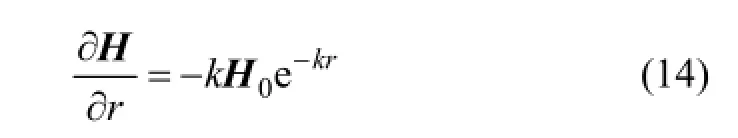
將式（13）兩邊分別乘以k并與式（14）相加，可得

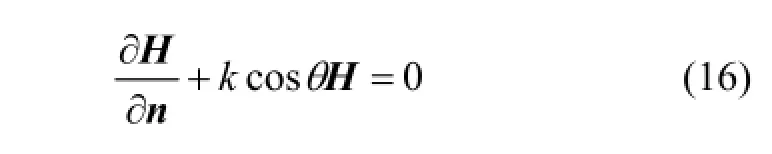
其中：n為模型邊界的外法線方向。將式（16）代入式（12）右邊第1式可得

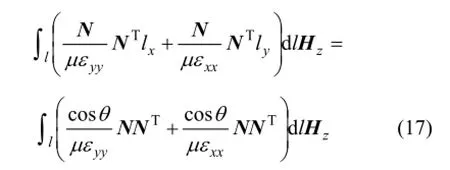
則式（12）可寫為

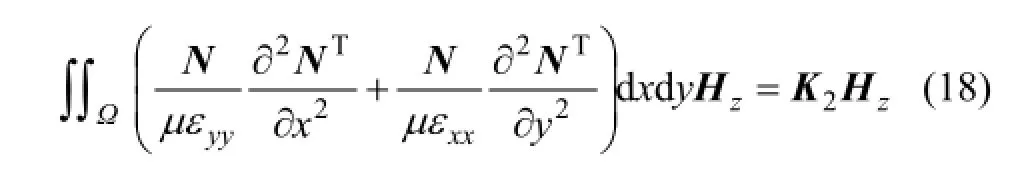
式中：

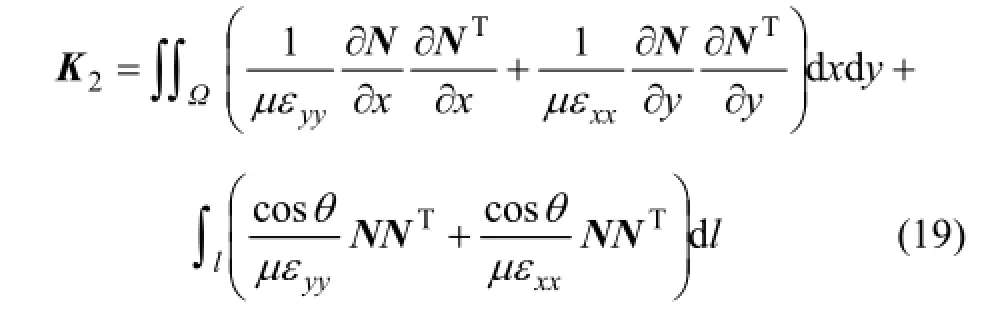
根據式（8）第 4項的推導方式，同理可推導式（8）中左邊第5項為

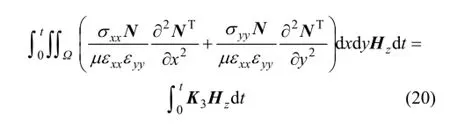
其中：剛度矩陣K3的表達式為

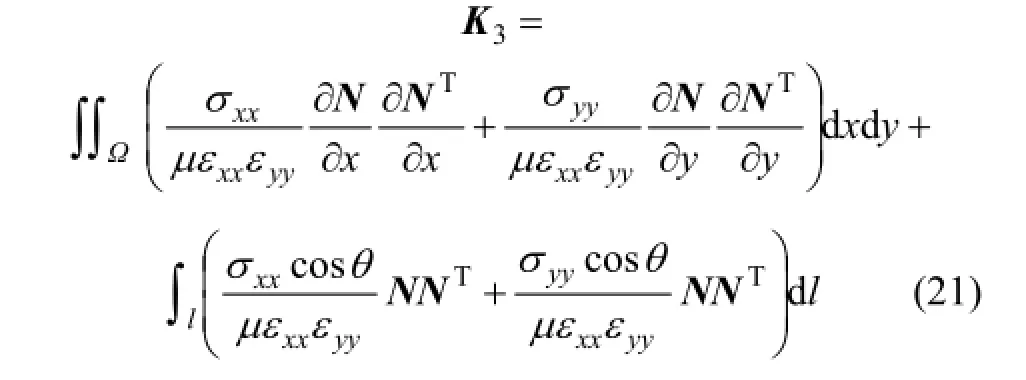
式（8）左邊第6項為

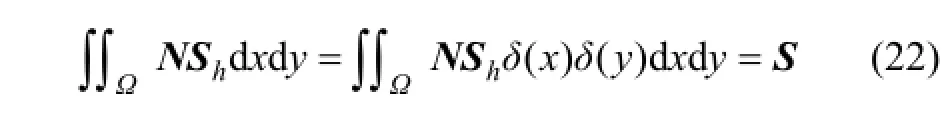
將式（9），（10），（11），（18），（20）和（22）代入式（8）可得

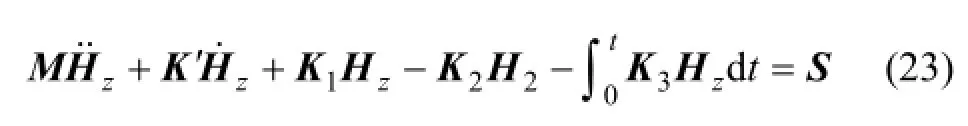
對時間域有限元方程式（23），采用中心差分法即可進行求解。將時間域［0 T］分為n等份，則采樣間隔為nTt/=Δ，在t時刻，

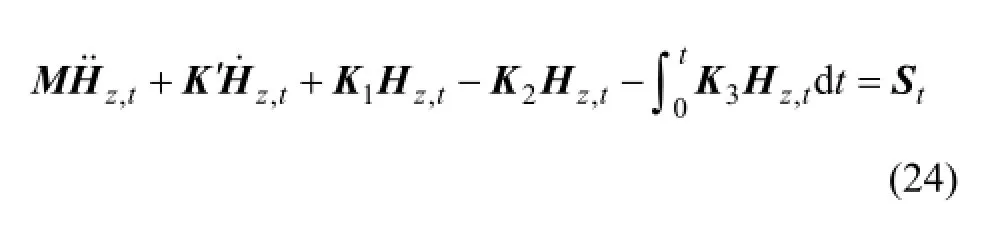
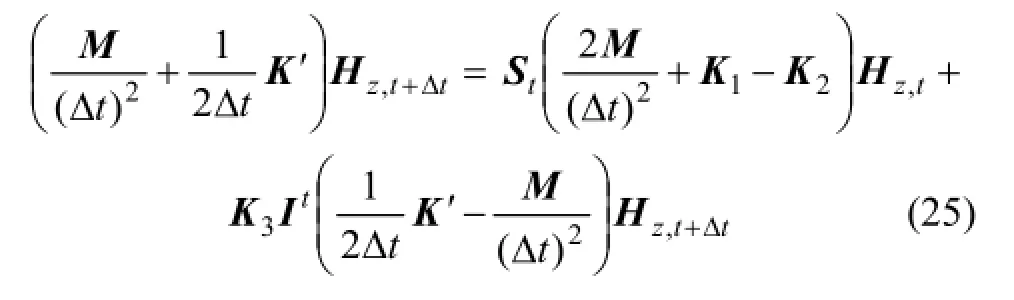
其中：tI的時間迭代格式為

式（25）和式（26）即為GPR有限元正演模擬時間遞推公式。由于零時刻的Hz，0，Hz，0和Hz，0以及tΔ-時刻的Hz，-Δt，Hz，-Δt和Hz，-Δt均為0，故根據式（25）和（26）可計算tΔ時刻的Hz，Δt，然后依次遞推可得到各個時刻的電場強度Hz。在求解式（25）時，選用不完全LU分解預處理的雙共軛梯度法BICGSTAB（biconjugate gradient stabilized）線性方程組求解算法［19］。該算法是一種高效迭代法，特別適用于求解方程組條件數很大的病態線性方程組。

3 數值算例

3.1 非結構化網格有限元正演算法的正確性驗證

依上述方法原理，編制了各向異性介質的GPR非結構化網格有限元正演源程序。利用該程序分別對均勻各向異性和均勻各向同性介質模型進行計算，并與均勻各向同性介質的時域有限差分法的結果與解析解進行對比，以驗證程序的正確性。

圖2所示為均勻各向異性介質解析解、FDTD 和FEM正演單道波形對比結果。從圖2可見： FEM 和FDTD的正演結果與解析解都非常吻合，但在波峰和波谷處，還存在一定差異，FEM的結果更靠近解析解，而FETD的結果在波峰和波谷處擬合較差。經過計算，在6.0～10.0 ns之間，FDTD的相對誤差為1.2%，而FEM 的相對誤差為 0.63%，由此可見基于非結構Delaunay網格的有限元法與FDTD算法相比具有更高的精度。這主要是由于非結構化Delaunay 相比FDTD中正方形網格剖分計算區域具有更小的離散誤差，局部加密技術能精確逼近電磁場的劇烈變化。

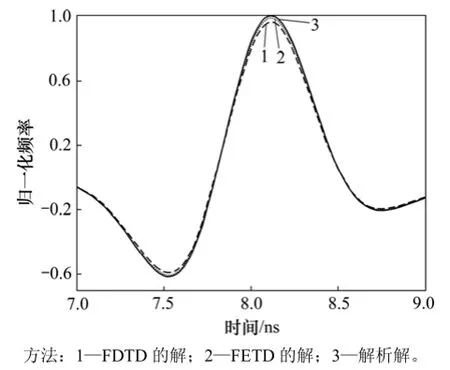
圖2 均勻各向異性介質解析解、FDTD和FEM正演單道波形對比Fig.2 Waveforms comparison among FETD results， FDTD results and analytical results for homogenous anisotropic media

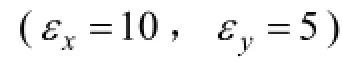
3.2 各向異性介質圓形異常體模型

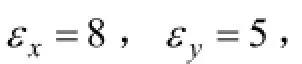
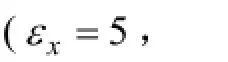
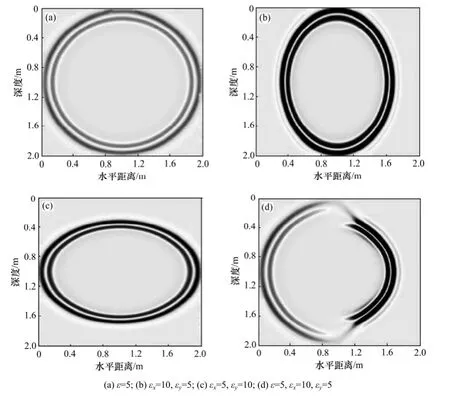
圖3 4種不同相對介電常數分布條件下各向異性介質模型在9 ns時刻的波場快照圖Fig.3 Snapshots of anisotropic models at 9 ns with four different permittivity distributions

圖4 各向異性介質Ⅰ圓形異常體非結構化網格剖分示意圖Fig.4 Schematic diagram of cylinder model discretized by unstructured meshes of Delaunay

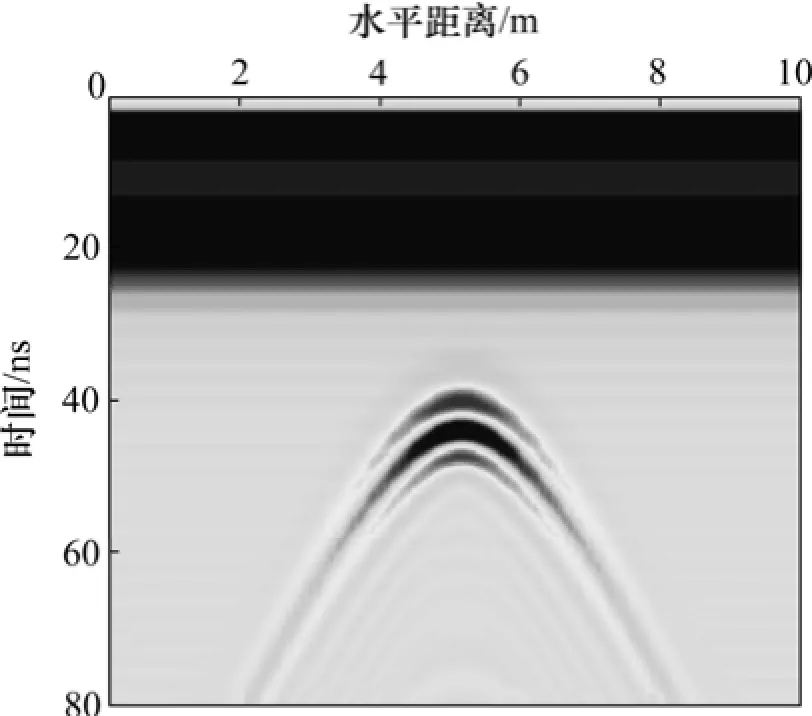
圖5 各向異性介質Ⅰ圓形異常體有限元正演剖面圖Fig.5 Simulated profile of cylinder model with isotropic background media

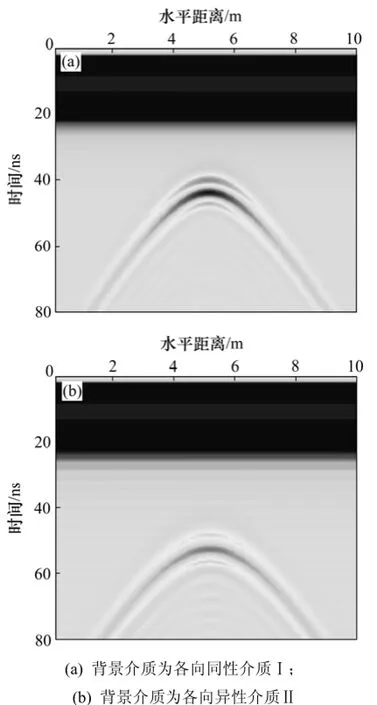
圖6 背景介質分別為各向同性介質Ⅰ和各向異性介質Ⅱ的GPR正演剖面圖Fig.6 GPR simulated profiles of circle model with anisotropic background mediaⅠand isotropic background mediaⅡ

4 結論

1） 從Maxwell方程組出發，在介質滿足單斜各向異性條件下，推導了時間域GPR波在各向異性介質中滿足的波動方程；并闡述了非結構化Delaunay網格有限單元法和中心差分法求解該波動方程的詳細解法。

2） 在同等條件下，非結構化網格有限元正演精度較傳統有限元精度有顯著提高。

3） 電磁波在各向異性介質中呈橢圓狀向外擴散傳播，其能量衰減較慢，與各向同性介質中圓形異常體反射波相比，各向異性介質中的反射波的曲率、能量和雙程走時受不同方向電磁波速度的影響會發生顯著變化。

［1］ 曾昭發， 劉四新. 探地雷達原理與應用［M］. 北京： 電子工業出版社， 2011： 168-169. ZENG Zhaofa， LIU Sixin. Ground penetrating radar theory and applications［M］. Beijing： Electronics Industry Press， 2010：168-169.

［2］ BATTISTA B M， ADDISON A D， KNAPP C C. Empirical model decomposition operator for Dewowing GPR data［J］. Journal of Environmental and Engineering Geophysics， 2009，14（4）： 163-169.

［3］ GOODMAN D. Ground-penetrating radar simulation in engineering and archaeology［J］. Geophysics， 1994， 59（2）：224-232.

［4］ SLOB E， SATO M， OLHOEFT G. Surface and borehole groundpenetrating-radar developments［J］. Geophysics， 2010， 75（5）：75A103-75A120.

［5］ GIFFORD C M， FINYOM G， JEFFERSON M， et al. Automated polar ice thickness estimation from radar imagery［J］. IEEE Transactions on Geoscience and Remote Sensing， 2010， 19（9）：2456-2469.

［6］ 魏兵. 各向異性介質電磁散射及參數反演研究［D］. 西安： 西安電子科技大學理學院， 2003： 1-2. WEI Bing. Study of electromagnetic scattering and reconstruction for anisotropic media［D］. Xi’an： Xiandian University. College of Science， 2003： 1-2.

［7］ 劉四新， 曾昭發， 徐波. 三維頻散介質中地質雷達信號的FDTD數值模擬［J］. 吉林大學學報（地球科學版）， 2006， 36（1）：123-127. LIU Sixin， ZENG Zhaofa， XU Bo. FDTD simulation for ground penetrating radar signal in 3-Dimensional dispersive medium［J］. Journal of Jilin University （Earth Science Edition）， 2006， 36（1）：123-127.

［8］ 劉四新， 曾昭發. 頻散介質中地質雷達波傳播的數值模擬［J］.地球物理學報， 2007， 50（1）： 320-326. LIU Sixin， ZENG Zhaofa. Numerical simulation for ground penetrating radar wave propagation in the dispersive medium［J］. Chinese Journal of Geophysics， 2007， 50（1）： 320-326.

［9］ GIANNOPOULOS A. Modeling ground penetrating radar by GprMax［J］. Construction and Building Materials， 2005， 19（10）：755-762.

［10］ JAMES I， ROSEMARY K. Numerical modeling of ground-penetrating radar in 2-D using MATLAB［J］. Computers & Geosciences， 2006， 32（9）： 1247-1258.

［11］ DI Qingyun， WANG Miaoyue. Migration of ground-penetrating radar data with a finite-element method that considers attenuation and dispersion［J］. Geophysics， 2004， 69（2）：472-477.

［12］ 戴前偉， 王洪華， 馮德山， 等. 基于三角形剖分的復雜 GPR模型有限元法正演模擬［J］. 中南大學學報（自然科學版）， 2012，43（7）： 2668-2673. DAI Qianwei， WANG Honghua， FENG Deshan， et al. Finite element method forward simulation for complex geoelectricity GPR model based on triangle mesh dissection［J］. Journal of Central South University （Science and Technology）， 2012， 43（7）：2668-2673.

［13］ 王洪華， 戴前偉. 基于UPML吸收邊界條件的GPR有限元數值模擬［J］. 中國有色金屬學報， 2013， 23（7）： 2003-2011. WANG Honghua， DAI Qianwei. Finite element numerical simulation for GPR based on UPML boundary condition［J］. The Chinese Journal of Nonferrous Metals， 2013， 23（7）： 2003-2011.

［14］ SCHNEIDER J， HUDSON S. The finite-difference time-domain method applied to anisotropic material［J］. IEEE Transactions on Antennas and Propagation， 1993， 41（7）： 994-999.

［15］ CARCIONE J M， SCHOENBERG M A. 3D ground-penetrating radar simulation and plane-wave theory in anisotropic media［J］. Geophysics， 2000， 65（5）： 1527-1541.

［16］ 王幫兵， 田鋼， 孫波， 等. 南極冰蓋內部結構特性研究： 基于三維各向異性電磁波時域有限差分方法［J］. 地球物理學報，2009， 52（4）： 966-975. WANG Bangbing， TIAN Gang， SUN Bo， et al. The study of the COF feature in the Antarctic ice sheet based on 3-D anisotropy FDTD method［J］. Chinese Journal of Geophysics， 2009， 52（4）：966-975.

［17］ 徐世浙. 地球物理中的有限單元法［M］. 北京： 科學出版社，1994： 266-275. XU Shize. Finite element method for geophysics［M］. Beijing：Science Press， 1994： 266-275.

［18］ KEY K， WEISS C. Adaptive finite element modeling using unstructured grids： the 2D magnetotelluric example［J］. Geophysics，2006， 71（6）： 291-299.

［19］ 柳建新， 蔣鵬飛， 童孝忠， 等. 不完全 LU分解預處理的BICGSTAB算法在大地電磁二維正演模擬中的應用［J］.中南大學學報（自然科學版）， 2009， 40（2）： 484-491. LIU Jianxin， JIANG Pengfei， TONG Xiaozhong， et al. Application of BICGSTAB algorithm with incomplete LU decomposition preconditioning to two-dimensional magnetotelluric forward modeling［J］. Journal of Central South University （Science and Technology）， 2009， 40（2）： 484-491.

（編輯 陳燦華）

GPR numerical simulation for anisotropic medium by using finite element method based on unstructured meshes

SHI Ming1，2， FENG Deshan1， WANG Honghua3， DAI Qianwei1

（1. School of Geosciences and Info-Physics， Central South University， Changsha 410083， China；2. Geophysical and Geochemical Prospecting Team，Non-ferrous Metals and Nuclear Industry Geological Exploration Bureau of Guizhou， Duyun 558004， China；3. College of Earth Sciences， Guilin University of Technology， Guilin 541004， China）

In order to more accurately understand the propagation law of GPR （ground penetrating radar） wave in anisotropic medium， the wave equations in monoclinic anisotropic medium were deduced based on the Maxwell equation，and the finite element method of unstructured meshes and the central difference method were applied to discretize in space domain and time domain respectively. Then， the GPR finite element numerical simulation algorithm of monoclinicanisotropic medium was built and programmed， and its feasibility and effectiveness were tested by comparing the results of simulation and analytical solution of homogenous anisotropic model. The finite element method based on unstructured meshes was applied to simulate the circle anisotropic model and homogeneous anisotropic model and compared with calculated results of its isotropic medium model. The results show that the simulated results by finite element method based on unstructured meshes have lower fitting error and higher precision compared with the simulated results by FDTD，the electromagnetic wave propagates outward with elliptical circle and its energy attenuates slower duo to the different velocities of wave in different directions. And curvature， energy and two way travel time of reflected wave change significantly compared with those of isotropic medium due to different wave velocitis in different directions.

anisotropic media； finite element method based on unstructured meshes； GPR （ground penetrating radar）；numerical simulation

P631

A

1672-7207（2016）05-1660-08

10.11817/j.issn.1672-7207.2016.05.027

2015-10-10；

2015-12-22

國家自然科學基金資助項目（41574116，41004053）；中南大學創新驅動項目（2015CX008）；中南大學教師研究基金資助項目（2014JSJJ001）；教育部新世紀優秀人才支持計劃項目（NCET-12-0551）；中南大學升華育英人才計劃項目（2012）；湖湘青年創新創業平臺培養對象項目（2013） （Projects（41574116， 41004053） supported by the National Natural Science Foundation of China； Project（2015CX008）supported by the Innovation Driven Program of Central South University； Project（2014JSJJ001） supported by the Teacher Research Fund of Central South University； Project（NCET-12-0551） supported by the New Century Excellent Talent Support Program of the Ministry of Education；Project（2012） supported by the Sublimation Yuying Talent Program of Central South University； Project（2013） supported by the Hunan Youth Innovation and Entrepreneurship Training Platform）

馮德山，教授，博士生導師，從事地球物理正反演與數據處理；E-mail： fengdeshan@126.com