堆石體在真三軸應力狀態下的非共軸性與剪脹特性

馬剛，劉嘉英，常曉林，周偉

（1. 武漢大學 水資源與水電工程科學國家重點實驗室，湖北 武漢，430072；2. 武漢大學 水工巖石力學教育部重點實驗室，湖北 武漢，430072）

堆石體在真三軸應力狀態下的非共軸性與剪脹特性

馬剛1，2，劉嘉英1，2，常曉林1，2，周偉1，2

（1. 武漢大學 水資源與水電工程科學國家重點實驗室，湖北 武漢，430072；2. 武漢大學 水工巖石力學教育部重點實驗室，湖北 武漢，430072）

基于連續-離散耦合分析方法，發展隨機顆粒不連續變形分析方法。采用不規則多面體模擬實際堆石顆粒，制備初始各向同性的堆石料數值試樣，進行等平均靜水壓力p、等中主應力系數b應力路徑的真三軸數值試驗。分析堆石料在真三軸應力狀態下的剪脹特性，以及應變增量與應力增量的非共軸性。研究結果表明：剛開始加載時，應變增量與應力增量共軸，隨著加載的進行，應變增量的方向發生偏轉，偏轉量與中主應力系數b有關，在三軸壓縮應力路徑（b=0）和三軸拉伸應力路徑（b=1）時，幾乎不發生偏轉；對比 Rowe，Roscoe，改進的 Roscoe以及Lagioia剪脹模型，改進的Roscoe剪脹模型預測的剪脹曲線與數值試驗結果較吻合，在改進的Roscoe剪脹模型上引入1個角隅函數，以反映中主應力對剪脹特性的影響。

堆石料；真三軸應力狀態；連續-離散耦合分析；非共軸性；剪脹特性

隨著我國社會經濟的快速發展以及西部水電開發進程的加快，西南地區正在或即將建設一批調節性能好的高堆石壩，壩高大多在200 m以上，有些甚至超過300 m，屬超高堆石壩工程。超高堆石壩的建設對堆石料力學特性的研究提出了更高的要求。目前，常規三軸試驗仍是研究堆石料力學特性的主要手段，現有的本構模型也大多基于堆石料的常規三軸試驗結果建立。常規三軸試驗只能模擬軸對稱應力狀態，無法考慮中主應力的影響，而實際工程中壩體的各個部位都處于三向不等的應力狀態，因此，有必要進行堆石料的真三軸試驗，研究堆石料在真三軸應力狀態下的變形和強度特性。國內外很多學者對砂土進行了真三軸試驗［1］，但是堆石料粒徑比砂土的粒徑要大得多，顆粒力學性質也與砂土存在較大差異，因此不能簡單地將砂土的真三軸試驗結果外推到堆石料中。由于缺乏大尺寸的真三軸試驗設備，目前堆石料的真三軸試驗成果很少。施維成［2］采用中型真三軸儀TSW-40對粗粒土進行了一系列的真三軸試驗，研究了中主應力對粗粒土強度和變形特性的影響， 并在此基礎上提出了一個粗粒土的三維破壞準則及雙屈服面三維彈塑性模型。施維成等［3］采用小型真三軸儀ZSY-1對礫石料進行了等 σ3、等b試驗，研究了中主應力對礫石料變形和強度的影響。XIAO等［4］整理了施維成［2］的粗粒土真三軸試驗結果，研究了圍壓、中主應力系數、試樣密度對粗粒土剪脹特性的影響，采用最小二乘法擬合試驗數據，提出了一個新的剪脹模型。除了試驗研究外，一些學者采用離散單元法進行了顆粒集合體在真三軸加載情況下的細觀數值模擬［5-9］，研究了顆粒集合體的細觀組構和接觸力在加載過程中的演化特性，從顆粒層面解釋了復雜力學特性的細觀機理。基于連續-離散耦合分析方法（combined finite-discrete element method，FDEM）［10］，周偉等［11］發展了隨機顆粒不連續變形分析方法（stochastic granular discontinuous deformation method，SGDD）。考慮實際堆石料一般由棱角狀和亞棱角狀的顆粒組成，提出了不規則多面體顆粒的隨機生成算法。馬剛等［12］采用SGDD方法進行了堆石料常規三軸剪切試驗的細觀數值模擬，再現了堆石料的非線性、壓硬性、剪脹和剪縮等主要力學特性。通過選擇合適的細觀參數，基于SGDD的細觀數值試驗具有較好的預測能力，為再現堆石料的宏觀力學特性、揭示其細觀力學機理提供了一條新的途徑。周偉等［13］采用SGDD進行了等σ3、等b應力路徑的真三軸數值試驗，從宏細觀2個層面研究了中主應力對堆石體變形和強度特性的影響。本文作者采用SGDD方法進行了堆石料在等p、等b應力路徑的真三軸數值試驗，采用伺服控制加載保持試樣的應力狀態按照預定的應力路徑變化。為了避免試樣初始各向異性的影響，各向等速壓縮松散顆粒集合體制備各向同性的數值試樣，顆粒形狀為不規則的凸多面體以接近真實的堆石顆粒形狀。著重分析了堆石料在真三軸應力狀態下的剪脹特性，以及應變增量與應力增量的非共軸性。

1 連續-離散耦合分析方法

連續-離散耦合分析方法結合了有限單元法和離散單元法，將基于有限單元法的連續介質力學分析與基于離散單元法的接觸檢索、接觸力計算和顯式動力學求解融合在一起。連續-離散耦合分析方法的提出是為了解決由大量可變形顆粒組成的顆粒集合體的瞬時動力學問題，顆粒間的接觸滿足互不侵入條件并傳遞法向和切向接觸力，在大多數情況下顆粒會發生斷裂、破碎和磨損，導致顆粒形狀的變化和顆粒數量的增多。

在連續-離散耦合分析中，通過變分形式簡化顆粒間接觸的理論假定，認為法向接觸力是法向侵入量的函數，而切向接觸力是法向接觸力和接觸狀態的函數。將接觸的邊界問題轉化為在接觸邊界域Γ構造泛函Π及其變分形式，在接觸邊界域Γ，接觸顆粒的位移場滿足：

接觸問題的變分形式需要在接觸邊界域Γ上構造一個泛函，通過尋找泛函的駐值來滿足不可貫入條件。為了接觸邊界域Γ上滿足接觸約束條件，定義泛函Π為

式中：p為罰參數。

由于：

若泛函Π在接觸邊界域Γ上為最小值，則罰參數p必須為正值。通過求解式（2）中修正泛函）（uΠ的極小值，近似滿足接觸約束條件。罰參數p越大，接觸約束條件的滿足程度越好，當罰參數無窮大時，接觸約束條件能夠精確滿足。在靜態或隱式動力學問題中，通過迭代求解的方法來精確滿足不可貫入條件。而在瞬時動力學問題中，放棄完全不可貫入條件，而采用足夠大的罰函數，使接觸的侵入量相對于顆粒尺寸來說可以忽略不計。

采用Munjiza-NBS算法檢索顆粒間的接觸，基于顆粒的有限元網格離散并結合接觸勢的概念進行接觸力分析。由于每個顆粒都被離散為單獨的有限元網格，因此在接觸力分析中，可以方便地使用有限元節點的幾何坐標來描述接觸顆粒的幾何形狀，并且接觸面上接觸力的分布更加真實。更重要的是，大大改善了接觸邊界附近的局部應變場的數值畸變性，當考慮顆粒材料的脆性斷裂和破碎時，這一點尤為重要。

采用二階四面體單元離散顆粒，如圖1所示。單元的中任意1點的位置矢量x和位移矢量u用形函數表示為：

式中：xi，yi和zi為第i個節點在全局坐標系下的坐標；ui，vi和 wi為第 i個節點在全局坐標系下的位移；Ni為第i個節點的形函數。

定義單元中任意1點在全局坐標系中的初始位置矢量xi為

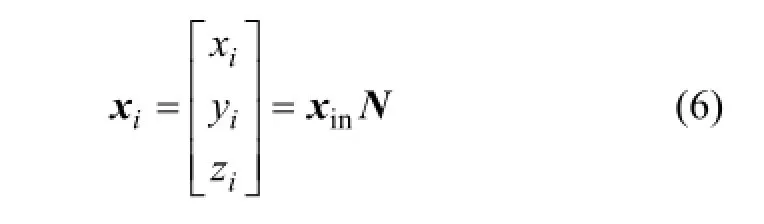
式中：xin為單元節點的初始位置矩陣；N為形函數矩陣。

單元中任意1點在全局坐標系中的當前位置矢量xc為

式中：xcn為單元節點的當前位置矩陣。

此時變形梯度張量F可表示為

定義變形梯度張量 F的行列式為 Jacobian行列式：

由變形梯度張量F定義右置的Cauchy-Creen張量為

采用 Neo-Hookean模型來計算單元的應力，Neo-Hookean模型是各向同性線彈性模型的擴展，適用于可壓縮的Neo-Hookean材料在大變形情況下的應力計算。此時，Cauchy應力矢量T可表示為

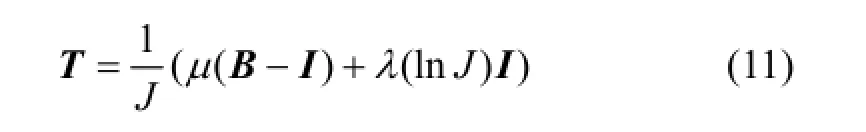
式中：μ和λ為拉梅常數。

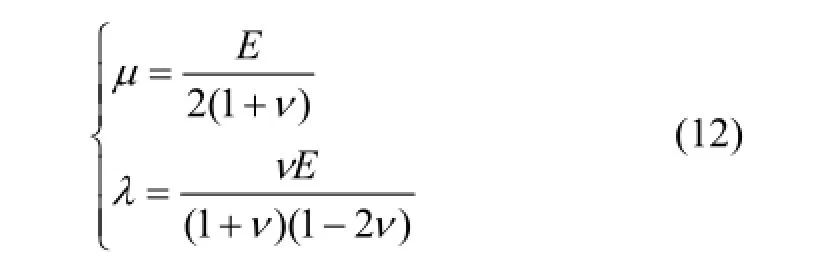
式中：E為彈性模量；v為泊松比。

圖1 二階四面體單元Fig.1 Quadratic tetrahedron element

2 真三軸數值試驗

2.1 數值試樣

制備數值試樣時，首先采用隨機顆粒生成程序RPG在1個較大的立方體空間內生成不接觸的松散顆粒集合體。將顆粒集合體信息導入堆石料細觀數值模擬軟件SGDD中，為了避免由制樣產生的初始各向異性，在試樣的各個方向采用位移控制等速地壓縮試樣直至目標大小，如圖3所示。在此過程中顆粒間的滑動摩擦角和重力加速度都設為 0，且顆粒不發生損傷和破碎。最終生成的數值試樣如圖4（a）所示，試樣形狀為立方體，其長×寬×高為300 mm×300 mm× 300 mm，共包含8 927個不規則凸多面體顆粒，試樣中顆粒的等效粒徑分布如圖4（b）所示，采用二階四面體單元離散為142 277個單元，401 590個節點。

由于采用各向等速地壓縮制備試樣，其組構和接觸力的空間分布沒有表現出明顯的各向異性。采用傅里葉函數來擬合顆粒間接觸法向、粒間法向接觸力和切向接觸力與角度的關系，其數學表達式為：

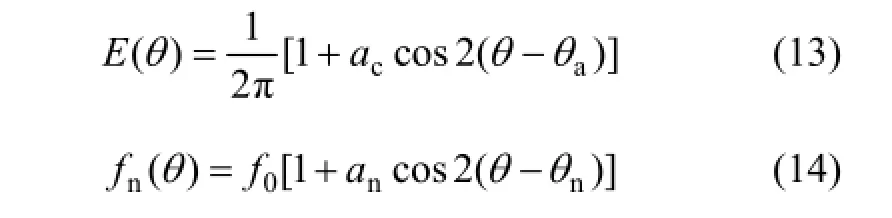
式中：θ為細觀組構量與剪切方向的夾角；f0為所有顆粒法向接觸力的平均值； θa和 θn分別為接觸法向和法向接觸力各向異性的主方向；ac和an為傅里葉系數，其數值分別反映接觸法向和法向接觸力的各向異性程度。

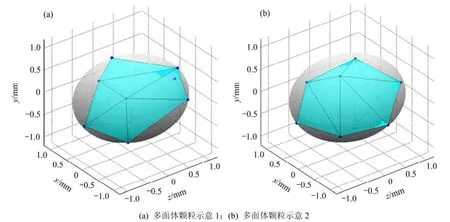
圖2 不規則多面體顆粒示意圖Fig.2 Sketch map of irregular polyhedral particle

圖3 各向等壓制備試樣Fig.3 Sample preparation by isokinetic triaxial compressing loose particle assembly

圖4 數值試樣及試樣中顆粒的等效粒徑分布Fig.4 Numerical sample and equivalent particle size distribution

接觸法向分布在3個平面上的各向異性系數ac分別為0.022，0.044和0.018，法向接觸力分布在3個平面上的各向異性系數an分別為0.012，0.011和0.008，因此可以認為數值試樣是初始各向同性的。

2.2 細觀參數

數值試驗所需要的細觀參數較多，其中部分參數可以通過常規物理力學試驗直接確定，比如顆粒密度、顆粒彈性模量和泊松比等，還有部分參數可參照一般巖石的取值范圍來確定，比如顆粒母巖的內摩擦角、單軸抗壓與抗拉強度之比。

除此之外還有顆粒間摩擦角φu、法向接觸剛度Kn、切向接觸剛度Ks、顆粒單軸抗壓強度fc和損傷閥值Rn等。本文的真三軸數值試驗不針對具體工程的堆石料，只是在一般堆石料的參數取值范圍內選取了一套參數進行數值模擬，所用參數見表1。

表1 堆石料真三軸數值試驗所用的細觀參數Table 1 Micro-parameters of rockfill in true triaxial numerical test

2.3 應力應變不變量

描述堆石料真三軸應力狀態的應力不變量有廣義剪應力q、平均靜水壓力p和應力羅德角 θσ：

2.4 加載路徑

首先給試樣施加三向等壓應力直至達到預定的圍壓值，然后再進行等p、等b應力路徑的剪切試驗。剪切時，在試樣軸向進行位移控制加載，在試樣的2個側面施加應力控制邊界條件，在此過程中保持靜水壓力p和中主應力系數b不變，直至試驗結束。在加載過程中，試樣的軸向為大主應力方向，大主應力σ1為

聯立以下2式：

可得施加在試樣 2個側面的中主應力σ2和小主應力3σ分別為：

在加載過程中，通過伺服控制機制動態調整作用在2個側面上的集中力荷載F2和F3：

分別進行了平均靜水壓力p為2.4 MPa，中主應力系數b為0，0.25，0.50，0.75和1.00的等p、等b應力路徑的真三軸數值試驗，三維應力空間下的應力路徑見圖5。其中，b=0對應三軸壓縮試驗（TC），b= 0.50對應簡單剪切試驗（SS），b=1.00對應三軸拉伸試驗（TE）。

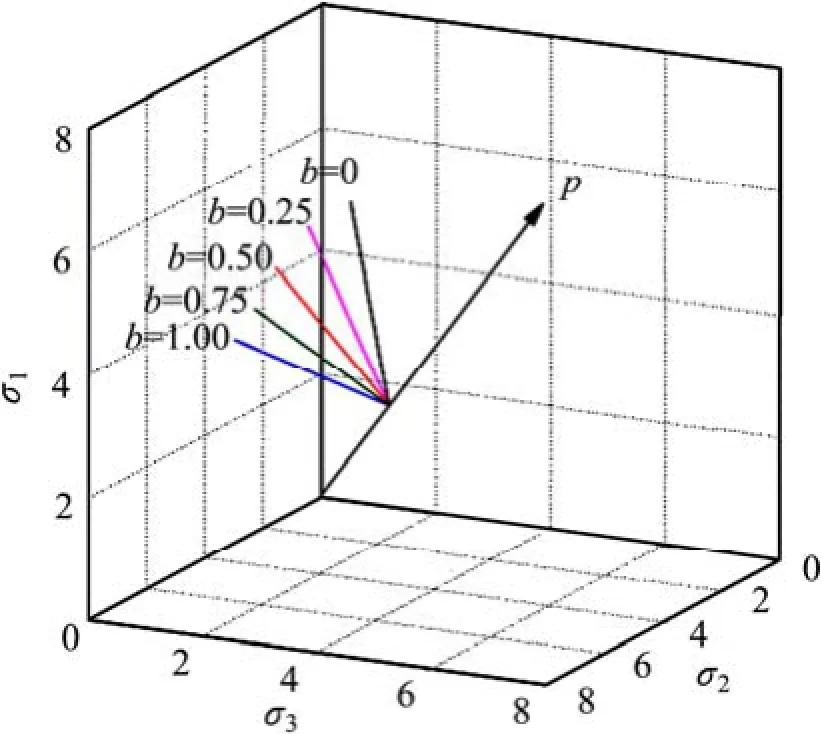
圖5 真三軸數值試驗應力路徑Fig.5 Stress paths of true triaxial tests

3 宏觀應力應變關系

隨著中主應力系數b的增大，顆粒集合體的剪應力與大主應變曲線的初始段斜率越來越大，峰值剪應力及其對應的大主應變卻逐漸減小。最大的峰值剪應力出現在b=0時，此時為三軸壓縮應力路徑，而b=1.00時，顆粒集合體的峰值剪應力最小，此時為三軸拉伸應力路徑，這個規律與已有的室內試驗和離散元模擬結果相似。不同中主應力系數b時，試樣的體積響應不同，在經過短暫而微小的壓縮變形后，試樣進入剪脹狀態，進入剪脹時對應的大主應變和剪脹變形都與中主應力系數b有關。具體來說，隨著中主應力系數b的增大，顆粒集合體更快的進入剪脹狀態，且剪脹體變更大。偏應力隨大主應變的演化曲線與剪應力比較相似，區別在于b=0和b=0.25時偏應力差別不大，而不像剪應力應變曲線那樣呈現出明顯的單調變化趨勢，比如在BARRETO等［8］的離散元模擬中，b=0.25時的偏應力就大于b=0時的偏應力。

圖6 b不同時數值試驗結果與大主應變的關系曲線Fig.6 Simulated behaviors plotted as functions of major principal strain for different b values

本文的真三軸數值試驗以及THORNTON等［5，7-8］進行的離散元數值模擬試驗，顆粒集合體的剪應力均表現出微小的峰后軟化。產生這種現象的原因有2個：一是上述研究中所用數值試樣的寬高比均為 1.0，LADE［1］研究了試樣的寬高比對應變局部化或剪切帶的影響，他發現當試樣的高寬比為1.0時，剪切帶會與試樣頂部的加載板和底部的基座相交，相交會約束剪切帶的發展并使試樣的應變更加均勻；另一個可能是，本文數值試驗采用的是不規則的多面體顆粒，顆粒之間咬合作用較強，為顆粒集合體提供了一個更加穩定的細觀結構。

圖7 b不同時主應變之間的關系曲線Fig.7 Relationship between principal strains for different b values

圖7所示為主應變之間的關系曲線，中主應變、小主應變與大主應變之間均為非線性關系。不同中主應力系數b時，小主應變始終為負值，表明在加載過程中試樣在小主應力方向始終發生膨脹，膨脹變形量隨中主應力系數b的增大而增大。試樣在中主應力方向的變形方向與中主應力系數b有關，在平面應變條件下，試樣在中主應力方向既不膨脹也不收縮，此時對應的中主應力系數為bps。當b＜bps時，中主應變對應膨脹變形；當b＞bps時，中主應變對應收縮變形。

圖8所示為偏主應變之間的關系曲線。與主應變之間的非線性關系不同，偏主應變之間近似為線性關系。偏主應變之間的關系曲線可以用下式擬合：

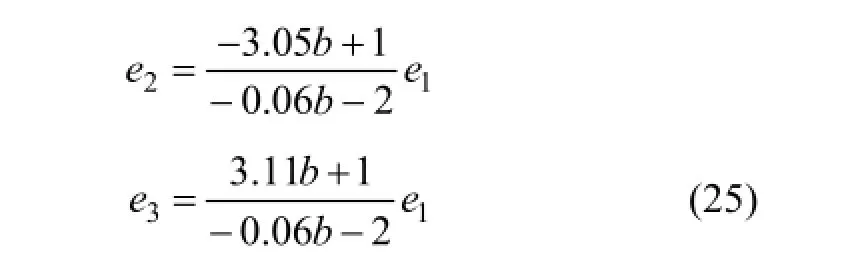
式（25）預測的結果與數值模擬結果擬合得非常好。

圖8 b不同時偏主應變之間的關系曲線Fig.8 Relationship between principal deviatoric strains for different b values

4 非共軸性

大量的工程實測結果和計算分析均表明：堆石壩內堆石料在填筑期的應力路徑近似為等應力比的路徑［14］。蓄水期上游堆石料內的小主應力方向接近于大壩上游面法向方向，水庫蓄水過程中，由于水荷載的作用方向與竣工期壩體內小主應力方向大體一致，隨著水荷載的增加，使壩軸線上游側小主應力增大，而偏應力減小，大小主應力比發生明顯的變化，主應力方向也將發生明顯的旋轉，這將導致主應力方向和主應變率方向的不一致，即非共軸性。目前對堆石料所開展的試驗研究幾乎都是常規三軸剪切試驗，屬于等比例加載條件，故不能反映堆石料的非共軸性。

定義加載過程中試樣的應力羅德角 θσ和應變羅德角 θε為（如圖9所示）：

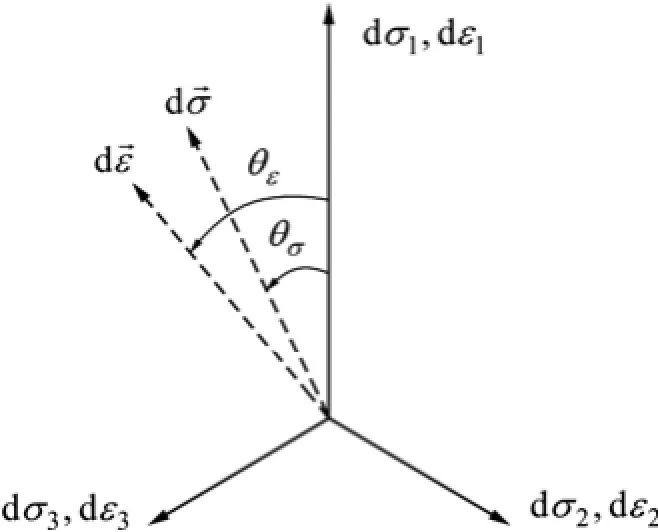
圖9 應力羅德角 θσ和應變羅德角 θε的定義Fig.9 Definitions of stress lode angle and strain lode angle

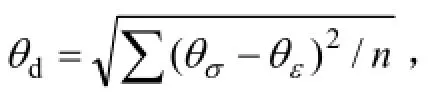
圖10 應力羅德角和應變羅德角隨大主應變的變化Fig.10 Evolutions of stress lode angle and strain lode angle with major principal strain

5 剪脹特性

ROWE［16］分析了顆粒材料的剪脹特性，將剪脹因子d表示為

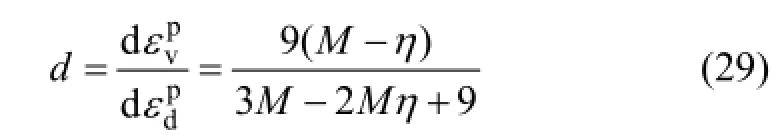
在Roscoe剪脹模型中，剪脹因子d隨應力比η線性變化，導致預測的剪脹特性與試驗結果差別較大。為了改進Roscoe剪脹模型，JEFFERIES等［17-20］在式（28）中引入了1個常數λ：

此外，LAGIOIA等［21］提出了1個適應性更好的剪脹模型：式中：α和λ為模型參數，當η趨近0，d趨向于無窮，表明在各向同性加載情況下出現單純的體積變形。

圖11所示為以上4個剪脹模型預測的剪脹曲線與數值試驗結果的對比。Roscoe剪脹模型和Rowe剪脹模型的預測能力較差，與數值試驗結果相差較遠。而Roscoe剪脹模型的2個改進形式，式（30）和式（31）的預測曲線與數值試驗結果較吻合。考慮到式（30）的簡潔性以及較好的預測能力，在接下來的研究中將采用這個剪脹模型來描述堆石料的剪脹特性。

圖11 不同剪脹模型預測剪脹特性與數值試驗結果對比Fig.11 Comparison of simulated dilatancy behavior with predications by different dilatancy models

圖12 不同中主應力系數的應力剪脹曲線Fig.12 Stress-dilatancy relations along different stress paths

圖12所示為靜水壓力為2.4 MPa時，不同中主應力系數b的應力比q/p與增量應變比dεv/dεd的關系曲線。不同中主應力系數b時，應力比與增量應變比之間近似為線性關系。采用式（30）擬合各子圖中的數值試驗結果，擬合曲線的斜率為λ，與η軸的交點為特征應力比M。可見：不同中主應力系數b時，擬合剪脹曲線的特征應力比和斜率不同，表現出了中主應力相關性。為了反映中主應力的影響，將特征應力比M和斜率λ表示為中主應力系數 b或者應力羅德角σθ 的函數：

圖13 剪脹模型的預測值與數值試驗結果對比Fig.13 Comparisons of dilatancy parameters between predictions and simulated results

采用一個統一的角隅函數來描述特征應力比和曲線斜率與中主應力系數的關系：

式中：a為擬合參數；k為三軸拉伸情況下的特征應力比與三軸壓縮情況下的比值。由圖13可以看出：本文采用的角隅函數擬合效果較好。

6 結論

1） 隨著中主應力系數b的增大，顆粒集合體的剪應力與大主應變關系曲線的初始段斜率越來越大，峰值剪應力及其對應的大主應變卻逐漸減小。最大的峰值剪應力出現在b=0時，此時為三軸壓縮應力路徑，而b=1.00時，顆粒集合體的峰值剪應力最小，此時為三軸拉伸應力路徑。

2） 在經過短暫而微小的壓縮變形后，試樣進入剪脹狀態，進入剪脹時對應的大主應變和剪脹變形的大小都與中主應力系數b有關。具體來說，隨著中主應力系數b的增大，顆粒集合體更快地進入剪脹狀態，且剪脹體變更大。

3） 應變羅德角 θε剛開始時與應力羅德角 θσ重合，隨著加載的進行，應變羅德角 θε開始偏移應力羅德角 θσ，開始出現非共軸性。偏轉量與中主應力系數b有關，在三軸壓縮應力路徑（b=0）和三軸拉伸應力路徑（b=1.00）時，幾乎不發生偏轉。

4） 對比了 Rowe，Roscoe，改進的 Roscoe以及Lagioia剪脹模型，改進的Roscoe剪脹模型預測的剪脹曲線與數值試驗結果較吻合，在改進的Roscoe剪脹模型上引入1個角隅函數，以反映真三軸應力狀態下的剪脹特性。

［1］ LADE P V. Assessment of test data for selection of 3-D failure criterion for sand［J］. International Journal for Numerical and Analytical Methods in Geomechanics， 2006， 30（4）： 307-333.

［2］ 施維成. 粗粒土真三軸試驗與本構模型研究［D］. 南京： 河海大學巖土工程科學研究所， 2008： 1-2. SHI Weicheng. True triaxial tests on coarse-grained soils and study on constitutive model［D］. Nanjing： Hohai University. Geotechnical Research Institute， 2008： 1-2.

［3］ 施維成， 朱俊高， 劉漢龍. 中主應力對礫石料變形和強度的影響［J］. 巖土工程學報， 2008， 30（10）： 1449-1453. SHI Weicheng， ZHU Jungao， LIU Hanlong. Influence of intermediate principal stress on deformation and strength of gravel［J］. Chinese Journal of Geotechnical Engineering， 2008，30（10）： 1449-1453.

［4］ XIAO Y， LIU H L， ZHU J G， et al. Dilatancy equation of rockfill material under the true triaxial stress condition［J］. Science China Technological Sciences， 2011， 54（Suppl1）：175-184

［5］ THORNTON C. Numerical simulations of deviatoric shear deformation of granular media［J］. Geotechnique， 2000， 50（1）：43-53

［6］ NG T T. Macro-and micro-behaviors of granular materials under different sample preparation methods and stress paths［J］. International Journal of Solids and Structures， 2004， 41（21）：5871-5884

［7］ MAHMUD SAZZAD M， SUZUKI K， MODARESSIFARAHMAND-RAZAVI A. Macro-micro responses of granular materials under different b values using DEM［J］. International Journal of Geomechanics， 2012， 12（3）： 220-228

［8］ BARRETO D， O’SULLIVAN C. The influence of inter-particle friction and the intermediate stress ratio on soil response under generalised stress conditions［J］. Granular Matter， 2012， 14（4）：505-521.

［9］ 周偉， 謝婷蜓， 馬剛， 等. 基于顆粒流程序的真三軸應力狀態下堆石體的變形和強度特性研究［J］. 巖土力學， 2012， 33（10）：3006-3012. ZHOU Wei， XIE Tingting， MA Gang， et al. Stress and deformation analysis of rockfill in true triaxial stress conditions based on PFC［J］. Rock and Soil Mechanics， 2012， 33（10）：3006-3012.

［10］ MUNJIZA A. The combined finite-discrete element method［M］. New York： John Wiley & Sons Ltd， 2004： 1-2.

［11］ 周偉， 常曉林， 周創兵， 等. 堆石體應力變形細觀模擬的隨機散粒體不連續變形模型及其應用［J］. 巖石力學與工程學報，2009， 28（3）： 491-499. ZHOU Wei， CHANG Xiaolin， ZHOU Chuangbing， et al. Stochastic granule discontinuous deformation model of rockfill and its application［J］. Chinese Journal of Rock Mechanics and Engineering 2009， 28（3）： 491-4995.

［12］ 馬剛， 周偉， 常曉林， 等. 堆石體三軸剪切試驗的三維細觀數值模擬［J］. 巖土工程學報， 2011， 33（5）： 746-753. MA Gang， ZHOU Wei， CHANG Xiaolin， et al. 3D mesoscopic numerical simulation of triaxial shear tests for rockfill［J］. Chinese Journal of Geotechnical Engineering， 2011， 33（5）：746-753.

［13］ 周偉， 劉東， 馬剛， 等. 基于隨機散粒體模型的堆石體真三軸數值試驗研究［J］. 巖土工程學報， 2012， 34（4）： 748-755. ZHOU Wei， LIU Dong， MA Gang， et al. Numerical simulation of true triaxial tests on mechanical behaviors of rockfill based on stochastic granule model［J］. Chinese Journal of Geotechnical Engineering， 2012， 34（4）： 748-755.

［14］ 柏樹田， 周曉光， 晁華怡. 應力路徑對堆石變形特性的影響［J］. 水力發電學報， 1999（4）： 76-80. BAI Shutian， ZHOU Xiaoguang， CHAO Huayi. Effects of stress path on the deformation of rockfill materials［J］. Journal of Hydroelectric Engineering， 1999（4）： 76-80.

［15］ ROSCOE K H， SCHOFIELD A N， THURAIRAJAH A. Yielding of clays in states wetter than critical［J］. Geotechnique， 1963，13（3）： 211-240

［16］ ROWE P W. The stress-dilatancy relation for static equilibrium of an assembly of particles in contact［C］// Proceedings of the Royal Society of London A： Mathematical， Physical and Engineering Sciences. London： The Royal Society， 1962：500-527.

［17］ JEFFERIES M G. Nor-Sand： a simple critical state model for sand［J］. Geotechnique， 1993， 43（1）： 91-103

［18］ GAJO A， WOOD M. Severn-trent sand： a kinematic-hardening constitutive model： the q-p formulation［J］. Geotechnique， 1999，49（5）： 595-614

［19］ LI X S， DAFALIAS Y F， WANG Z L. State-dependant dilatancy in critical-state constitutive modelling of sand［J］. Canadian Geotechnical Journal， 1999， 36（4）： 599-611

［20］ YANG Y， MURALEETHARAN K K. The middle surface concept and its application to the elasto-plastic behaviour of saturated sands［J］. Geotechnique， 2003， 53（4）： 421-431

［21］ LAGIOIA R， PUZRIN A M， POTTS D M. A new versatile expression for yield and plastic potential surfaces［J］. Computers and Geotechnics， 1996， 19（3）： 171-191.

（編輯 楊幼平）

Non-coaxiality and dilatancy of rockfill materials under true triaxial stress condition

MA Gang1，2， LIU Jiaying1，2， CHANG Xiaolin1，2， ZHOU Wei1，2

（1. State Key Laboratory of Water Resources and Hydropower Engineering Science， Wuhan University，
Wuhan 430072， China；2. Key Laboratory of Rock Mechanics in Hydraulic Structural Engineering of Ministry of Education，Wuhan University， Wuhan 430072， China）

Based on the combined finite-discrete element method， the stochastic granular discontinuous deformation method was developed. Numerical samples composed of irregular polyhedras were compressed to the isotropical state and then subjected to true triaxial loading with the constant mean stress and the constant intermediate principal stress ratio. The dilatancy of rockfill materials was analyzed， as well as the non-coaxiality of the stress increment and the strain increment. The results show that the strain increment and stress increment are coaxial at first， and then the direction of the strain increment has some deflection which is related to the intermediate principal stress ratio. No deflection is shown in the triaxial compression and extension path. The comparison of the Rowe’s， Roscoe’s， modified Roscoe’s and Lagioia’s models indicates that the dilatancy curve predicted by modified Roscoe’s model fits well with the simulated results. A ridge function is introduced to describe the influence of the intermediate principal stress ratio on the dilatancy.

rockfill materials； true triaxial stress condition； combined FEM/DEM； non-coaxiality； dilatancy

TV641

A

1672-7207（2016）05-1697-11

10.11817/j.issn.1672-7207.2016.05.032

2015-06-26；

2015-08-25

（Foundation item）：國家自然科學基金資助項目（51379161，51509190）；中央高校基本科研業務費專項資金資助項目（2042015kf0022）；博士后科學基金面上資助項目（2015M572195） （Projects（51379161， 51509190） supported by the National Natural Science Foundation of China；Project（2042015kf0022） supported by the Fundamental Research Funds for the Central Universities； Project（2015M572195） supported by China Postdoctoral Science Foundation）

馬剛，博士（后），講師，從事顆粒材料宏細觀多尺度力學特性研究；E-mail： magang630@whu.edu.cn