煤炭供應鏈牛鞭效應量化研究*

云小紅，張金鎖，金　浩

(1.西安科技大學 管理學院，陜西 西安 710054；2.西安科技大學 能源經濟與管理研究中心，陜西 西安 710054；3.延安大學 經濟管理學院，陜西 延安 716000；4.西安科技大學 理學院，陜西 西安 710054)

?

煤炭供應鏈牛鞭效應量化研究*

云小紅1，2，張金鎖3，金浩2，4

(1.西安科技大學 管理學院，陜西 西安 710054；2.西安科技大學 能源經濟與管理研究中心，陜西 西安 710054；3.延安大學 經濟管理學院，陜西 延安 716000；4.西安科技大學 理學院，陜西 西安 710054)

考慮一個煤炭勘探開采企業和一個煤炭銷售運輸企業組成的兩級煤炭供應鏈，建立了煤炭市場需求服從SARMA時間序列過程，煤炭銷售運輸企業采用MA技術預測市場需求和Order-up-to庫存策略的煤炭供應鏈牛鞭效應量化模型，并對該模型的影響因素進行理論分析和算例驗證。研究表明：0<ρ<1,0<θ<1時，煤炭供應鏈必會產生牛鞭效應；L≤k≤S時，牛鞭效應值較小；季節性自回歸系數、季節性移動平均系數、季節性循環周期、訂貨提前期和歷史數據個數5個參數對煤炭供應鏈牛鞭效應有直接影響。具體而言，季節性循環周期的增大有助于減少煤炭供應鏈牛鞭效應，季節性自回歸系數的增大并不總是能減少煤炭供應鏈牛鞭效應，而季節性移動平均系數和訂貨提前期的減少有助于減少煤炭供應鏈牛鞭效應。

牛鞭效應；煤炭供應鏈；季節性

0　引　言

牛鞭效應(Bullwhip Effect，BE)一直是國內官、產、學、研競相研究的焦點，供應鏈上需求信息的逐級放大引發了 “牛鞭效應”，沖擊著供應鏈上的供需平衡，導致供應過剩、產品積壓，無形中增加額外成本、增大產品損耗、打亂生產計劃，直接影響供應鏈的運作效率和經濟效益[1-3]。對于牛鞭效應的量化研究，Chen[4]等指出已有文獻量化牛鞭效應常運用不同的需求過程、庫存策略或預測技術。對于需求過程，學者們廣泛應用自回歸移動平均模型(ARMA)[5-7]，特別是它的特殊形式—簡單一階自回歸AR(1)模型[4，8]，李文立[9]研究AR(1)模式下分銷商利用歷史訂單數據如何減少牛鞭效應，劉紅等(2007)[10]的顧客需求采用AR(1)模型，并比較不同預測方法(移動平均(MA)、指數平滑(ES)、最小均方差(MMSE))下的牛鞭效應；馬云高(2012)[11-12]建立了需求依賴價格的AR(1)需求模型下，采用不同預測方法(MA,ES,MMSE)時的牛鞭效應，確定了零售商預測技術的選擇條件。對于預測技術，Chen,Zhang,馬云高[4，13，11]等分別應用移動平均(MA)、指數平滑(ES)和最小均方差(MMSE)預測技術預測提前期需求，并進一步證實移動平均預測下的牛鞭效應不如指數平滑預測下的結果顯著。馬云高在文獻[14]中指出移動平均技術是企業最為熟悉和常用的預測技術之一，相較于指數平滑技術，移動平均預測技術的應用前景更為廣闊。對于庫存策略，Wadhwa[15]研究了固定訂貨Q，Order-Up-To，(s，Q)，(s，S)4種庫存策略下的牛鞭效應，Chen，Zhang[4，13]應用經典的補充訂貨至目標庫存(Order-Up-To)策略對牛鞭效應進行分析。

綜上所述，傳統供應鏈中牛鞭效應的量化研究已經非常深入與成熟，許多研究考慮了需求是平穩的、非季節性的AR或ARMA模型，預測技術多采用MA，ES或MMSE，庫存多采用Order-Up-To策略。同樣，在煤炭供應鏈中已取得豐碩成果，尤磊學者證實煤炭市場AR(1)需求模式下同樣存在著煤炭需求信息沿煤炭供應鏈扭曲的現象[16]。然而，筆者在文獻[17]中證實：煤炭供應鏈使用AR或ARMA模型不如采用季節性自回歸移動平均(SARMA)模型模擬煤炭需求過程更接近煤炭實際市場需求，基于以上分析，文中構建煤炭市場需求服從SARMA需求模式，煤炭銷售運輸企業采用慣用的MA預測技術和經典的Order-Up-To庫存策略的煤炭供應鏈牛鞭效應的量化模型，希望借此抑制煤炭供應鏈牛鞭效應，緩解牛鞭效應對煤炭供應鏈的沖擊，提升煤炭供應鏈效率和效益，實現煤炭供應鏈健康、穩定發展。

1　煤炭供應鏈模型

1.1參數與假設

模型中涉及的參數、變量符號與定義見表1.

表1　各參數變量符號及其含義

Leeetal.[3]通過實證研究表明：多數產品的需求自回歸系數大于零。鑒于此，文中假設相鄰時期煤炭市場需求正相關，相鄰循環周期煤炭市場需求誤差正依存，考慮由一個煤炭勘探開采企業和一個煤炭銷售運輸企業組成的兩級供應鏈，如圖1所示。煤炭銷售運輸企業在t-1期末觀測到用戶(主要包括電力企業、冶金企業、建材企業和化工企業)需求Dt，并計算第t期目標庫存St，從而在t期初向煤炭勘探開采企業發出訂單訂貨qt，假設煤炭勘探開采企業能及時補充訂貨至目標庫存，煤炭銷售運輸企業經過提前期L后在t+L期初收到煤炭勘探開采企業的供貨。

圖1　煤炭兩級供應鏈Fig.1　Two-stage coal supply chain

1.2建立模型

1.2.1煤炭需求過程

煤炭主力消耗行業為電力、冶金、建材、化工等4大行業，這其中電力比例高達50%～60%，表明電力行業占據全國煤炭消費中的絕對優勢地位，其波動趨勢將代表4大用煤行業甚至全國煤炭消費量的波動趨勢。而電力消費受季節性因素影響較大，夏、冬兩季明顯高于春、秋兩季，致使電力生產量和電力生產所需的煤炭需求量存在季節性波動，因此，整個煤炭需求量帶有明顯的季節性波動趨勢，也就是說煤炭需求市場服從SARMA(1，0)X(0，1)s時間序列過程，那么煤炭市場需求模型為

Dt=μ+ρDt-1+εt-θεt-s.

(1)

式中μ為非負常數；0<ρ<1,0<θ<1為平穩可逆條件;εt為獨立同分布的隨機變量，且εt～N(0,σ2).

由式(1)可知煤炭市場需求均值和方差為

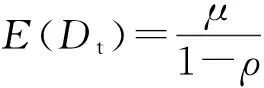
(2)

(3)

1.2.2煤炭庫存策略

煤炭庫存不足或者庫存過量都會影響煤炭用戶的穩步運行，增加煤炭用戶的運營壓力，進而影響其正常供應，因此，煤炭庫存多采用定期補充庫存策略中目標庫存水平的確定方法。

根據提前期需求預測值計算目標庫存St

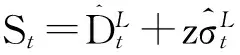
(4)

煤炭銷售運輸企業周期檢查庫存，為使t期末庫存水平保持在St，t期初煤炭銷售運輸企業向煤炭勘探開采企業發出的訂貨量qt為

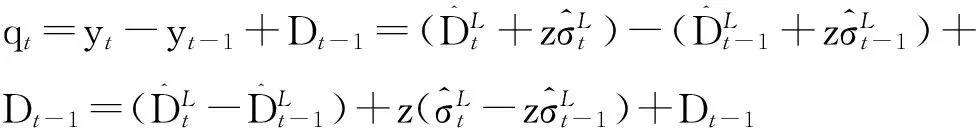
(5)

其中，訂貨量qt可以為負值，表示多余庫存可以無成本返回給煤炭勘探開采企業。

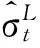
(6)

2　煤炭供應鏈牛鞭效應量化

Chen，Duc，Luong[4，18]等學者對牛鞭效應的量化是采用供應鏈系統中的訂貨波動方差與市場需求方差之比來描述的，文中采用此方法量化煤炭供應鏈牛鞭效應。其步驟如下：第一，計算提前期內需求預測值；第二，根據公式(6)計算訂貨量及其方差；第三，根據訂單方差與市場需求方差之比計算牛鞭效應的數值。

2.1MA預測技術

MA是一種操作簡單的平滑預測技術，該方法預測效果好，并將季節性因素考慮進去，煤炭銷售運輸企業可采用MA預測技術預測提前期內的煤炭市場需求。它的基本思想是：逐項推移，計算最近數期實際值的平均值作為未來一期的預測值。

第t期煤炭市場需求預測值為

(7)

非洲豬瘟病毒在原料中30天后的存活能力仍然未知，并且當前還沒有足夠的數據來準確估計。由于無法計算有效的隔離期，高風險的原科應該從無非洲豬瘟病毒和經典豬瘟病毒的國家引進。

(8)

2.2牛鞭效應量化

定理1煤炭銷售運輸企業運用移動平均技術(MA)預測提前期需求，則牛鞭效應BE表達式為

(9)

證明：將式(8)代入式(6)，整理后得煤炭銷售運輸企業訂貨量為

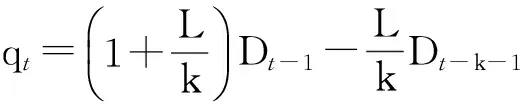
(10)

由式(10)求煤炭銷售運輸企業訂貨量方差為

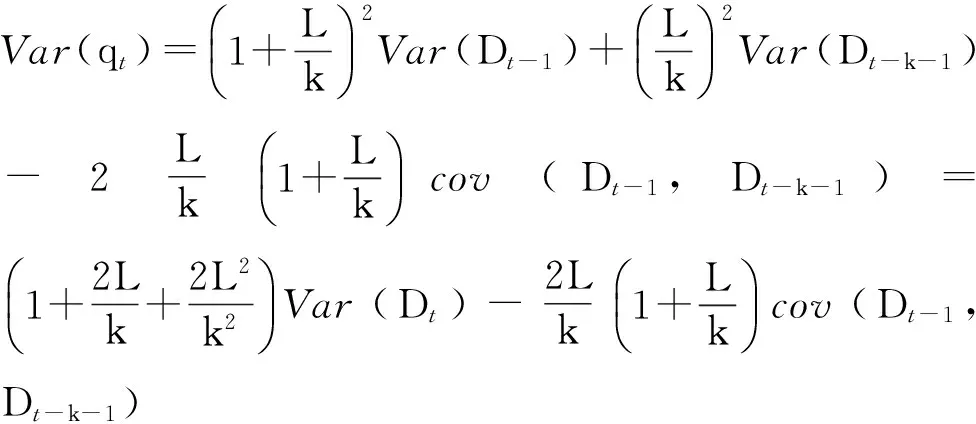
(11)

由式(1)可以推理出

Dt+i=μ+ρDt+i-1+εt+i-θεt-ε+i,

(12)

(13)

利用類似過程進行遞推，可以得出

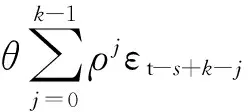
(14)

于是cov(Dt-1,Dt-k-1)=cov(Dt,Dt+k)=

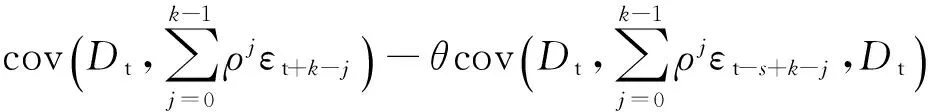
(15)

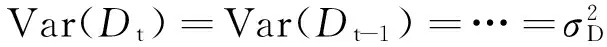
Var(εt-s)=Var(εt-s-1)=…=σ2,

cov(Dt,εt-s)=cov(Dt-2,εt-s-1)=…=ρs-1σ2,

cov(εt-s,εt-s-1)=0,cov(Dt-2,εt-1)=0,則

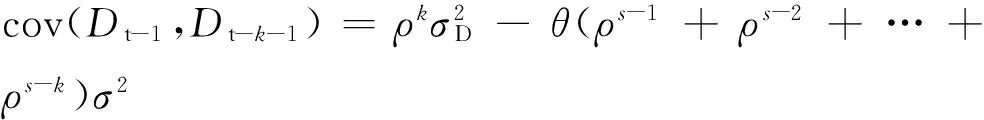
(16)

將式(3)代入式(16)并化簡可得煤炭銷售運輸企業訂貨量方差為

Var(qt)=

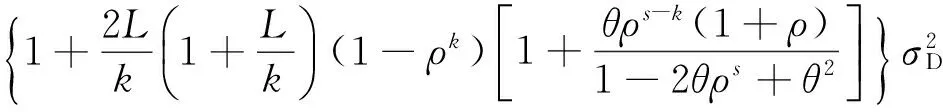
(17)

3　煤炭供應鏈牛鞭效應分析

由牛鞭效應表達式可知：MA預測技術下，煤炭供應鏈牛鞭效應值BE依賴以下5個參數：季節性自回歸系數ρ,季節性移動平均系數θ,季節性循環周期s,訂貨提前期L和歷史數據個數k.

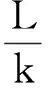
定理20<ρ<1,0<θ<1時，煤炭市場需求服從SARMA時間序列過程，MA預測技術下煤炭供應鏈必會產生牛鞭效應。

證明：由于0<ρ<1,k≥1，那么，1-ρk>0,ρs-k>0,

1-2θρs+θ2=(θ-ρs)2+1-2ρ2s>0,

(18)

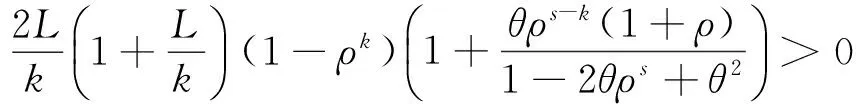
因此，可證定理。

定理30<ρ<1,0<θ<1時，煤炭市場需求服從SARMA時間序列過程，MA預測技術下，牛鞭效應值并不總是與季節性自回歸系數ρ反方向變化。

證明：

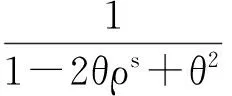
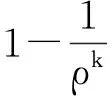
因此，定理可證。

定理40<ρ<1,0<θ<1時，煤炭市場需求服從SARMA時間序列過程，MA預測技術下煤炭供應鏈牛鞭效應值與季節性移動平均系數θ同方向變化。

證明：

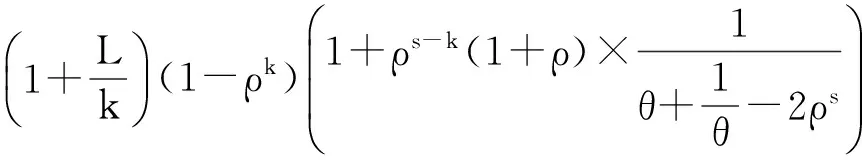
(19)

因此，可證定理。

定理50<ρ<1,0<θ<1時，煤炭市場需求服從SARMA時間序列過程，MA預測技術下煤炭供應鏈牛鞭效應值與訂貨提前期L同方向變化。

證明：由牛鞭效應的表達式可以直觀看出BE是關于L的遞增函數，即BE隨L增大而增大，BE隨L減小而減小，因此，可證定理。

定理60<ρ<1,0<θ<1時，煤炭市場需求服從SARMA時間序列過程，MA預測技術下煤炭供應鏈牛鞭效應值與季節性循環周期S反方向變化。

證明：

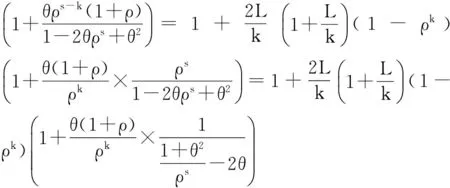
(20)

顯然，0<ρ<1時，S增大，ρs減少，BE減少；S減少，ρs增大，BE增大。

因此，可證定理。

4　算例驗證

1)當0<ρ<1,0<θ<1，煤炭市場需求遵循SARMA時間序列模型，在煤炭兩級供應鏈中采用MA預測技術和Order-Up-To庫存策略時煤炭供應鏈牛鞭效應的存在性；

2)煤炭供應鏈牛鞭效應值與季節性自回歸系數、季節性移動平均系數、訂貨提前期和季節性循環周期的變化方向。下面通過數值分析的方法驗證結論的正確性。

假定參數的不同取值，表2描述了在不同的季節性自回歸系數、季節性移動平均系數、訂貨提前期和季節性循環周期下，煤炭供應鏈牛鞭效應的存在性，這與尤磊等學者所得到的結論吻合[16]。從表2中可以看出，當L?k?S時，煤炭供應鏈牛鞭效應發生驟變。因此，減少牛鞭效應最有效的方法是調節L,k,S三者之間的相對關系，使得L≤k≤S.

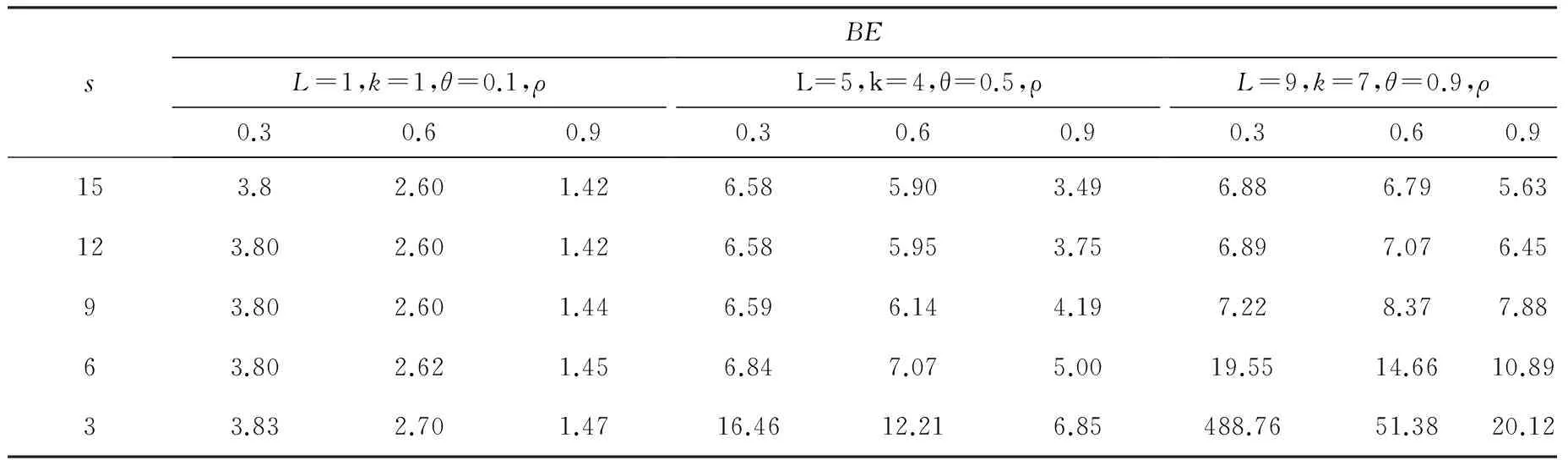
表2　MA預測下的牛鞭效應仿真值

令L=1,k=1,s=1,θ=0.1；L=6,k=12,s=15,θ=0.4和L=8,k=10,s=12,θ=0.5，表3描述了煤炭供應鏈牛鞭效應與季節性自回歸系數的關系，可以看出，牛鞭效應時而隨著季節性自回歸系數的增大而減少，時而隨著季節性自回歸系數的增大而增大，這與劉紅得出的結論類似[10]。這說明相鄰時期煤炭市場需求的相關性對煤炭供應鏈牛鞭效應的影響不確定。

令L=1,k=1,s=1,ρ=0.1；L=6,k=12,s=15,ρ=0.4和L=8,k=10,s=12,ρ=0.5，表4描述了煤炭供應鏈牛鞭效應與季節性移動平均系數的關系，可以看出，牛鞭效應隨著季節性移動平均系數的增大而增大，隨著季節性移動平均系數的減少而減少。因為季節性移動平均系數越大，相鄰循環周期的市場需求誤差越大，從而導致訂貨量波動越大，最終使得牛鞭效應越大，反之亦然。因此，減小相鄰循環周期的市場需求誤差的依存度可以減弱煤炭供應鏈牛鞭效應。

表4　季節性移動平均系數對牛鞭效應的影響

假設參數的不同取值，表5描述了一定的季節性自回歸系數、季節性移動平均系數、歷史數據個數和季節性循環周期下煤炭供應鏈牛鞭效應值同訂貨提前期的變化規律，觀察發現，牛鞭效應隨著訂貨提前期的增大而增大，這與Chen等學者的研究結論一致[4]。因為訂貨提前期越長，L備貨期內的需求總預測值越大，相應地，L備貨期內的訂貨量波動越大，從而導致牛鞭效應增大。因此，加強供應鏈成員之間的協調與合作可以有效緩解牛鞭效應帶來的危害。

表5　訂貨提前期對牛鞭效應的影響

令L=1,k=1,ρ=0.7,θ=0.9；L=2,k=4,ρ=0.8,θ=0.1和L=3，k=5,ρ=0.5,θ=0.5，表6描述了煤炭供應鏈牛鞭效應與季節性循環周期的關系，可以看出，牛鞭效應隨著季節性循環周期的減少而增大，牛鞭效應隨著季節性循環周期的增大而減少，這與Dong所得到的結論吻合[19]。因為季節性循環周期越長，備貨期內煤炭市場需求估計值及訂貨量越精準，進而訂貨量波動越小，最終導致牛鞭效應越小，反之亦然。

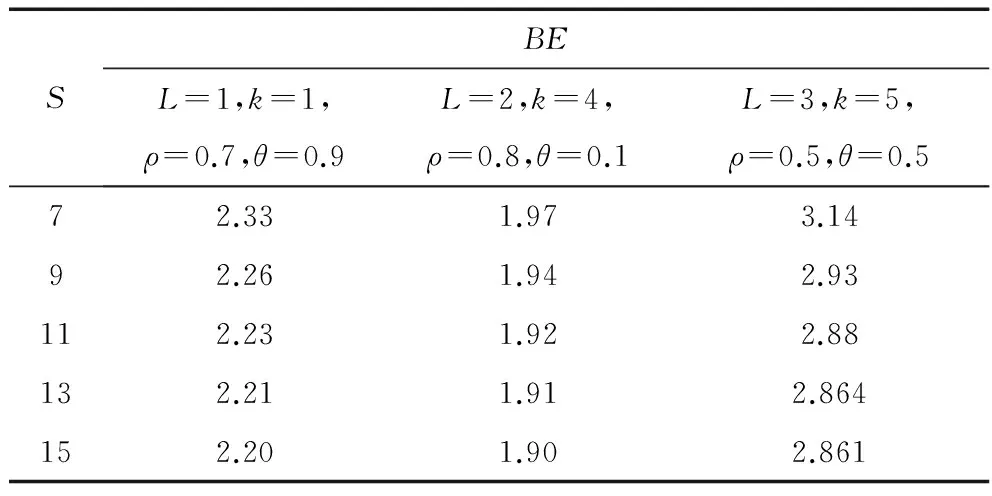
表6　季節性循環周期對牛鞭效應的影響

5　結　論

1)0<ρ<1,0<θ<1時，MA預測技術下煤炭供應鏈總會產生牛鞭效應，因此，煤炭供應鏈各成員應提前采取措施應對牛鞭效應產生的危害；

2)L，k,S三者之間的相對關系對BE值大小有顯著影響。當L≤k≤S時，煤炭供應鏈牛鞭效應值較小；當L

3)0<ρ<1,0<θ<1時，MA預測技術下，煤炭供應鏈牛鞭效應大小取決于季節性自回歸系數、季節性移動平均系數、季節性循環周期、訂貨提前期和歷史數據個數5個參數，具體來說，煤炭供應鏈牛鞭效應值與季節性循環周期反方向變化，煤炭供應鏈牛鞭效應值與季節性自回歸系數方向變化不確定；煤炭供應鏈牛鞭效應值與季節性移動平均系數和訂貨提前期同方向變化。因此，相鄰循環周期的煤炭市場需求誤差依存度越低、備貨期越短、季節性循環周期越長對抑制煤炭供應鏈牛鞭效應越有效。

References

[1]Forrester J W.Industrial dynamic：a major breakthrough for decision makers[J].Harvard Business Review，1958，36(4)：37-66.

[2]Sterman J D.Modeling managerial behavior：misperceptions of feedback in a dynamic decision making experiment[J].Management Science，1989，35(3)：321-339.

[3]Lee H L，Padmanabhan V，Whang S.Information distortion in a supply chain：the bullwhip effect[J].Management Science，1997，43(4)：546-558.

[4]Chen F，Drezner Z，Ryan J K．et al.Quantifying the bullwhip effect in a simple supply chain：the impact of forecasting，lead times，and information[J].Management Science，2000，46(3)：436-443．

[5]Disney S M，Farasyn I，Lambrecht M．Taming the bullwhip effect whilst watching customer service in a single supply chain echelon[J].European Journal of Operational Research，2006，173(1)：151-172．

[6]Gilbert K．An ARIMA supply chain model[J].Management Science，2005，51(2)：305-310．

[7]劉紅，王平．基于ARMA(1，1)需求的多級供應鏈牛鞭效應真[J].系統仿真學報，2008，20(12)：3 253-3 256．

LIU Hong，WANG Ping．Bullwhip effect molding and simulation analysis in multi-level supply chain for ARMA(1，1)demand model[J].Journal of System Simulation，2008，20(12)：3 253-3 256．

[8]Lee H L，So K C，Tang C S g S．The value of information sharing in a two-level supply chain[J].Management Science，2000，46(5)：626-643．

[9]李文立，王樂超．歷史訂單信息對牛鞭效應的影響分析[J].運籌與管理，2012，21(1)：195-200．

LI Wen-li，WANG Le-chao.Analysis of the affect of the history order information on the bullwhip effect[J].Operations Research and Management Science，2012，21(1)：195-200．

[10]劉紅，王平．基于不同預測技術的供應鏈牛鞭效應分析[J].系統工程理論與實踐，2007(7)：26-33.

LIU Hong，WANG Ping．Bullwhip effect analysis in supply chain for demand forecasting technology[J].System Engineering Theory and Practice，2007(7)：26-33.

[11]馬云高，王能民，徐金鵬.供應鏈零售商預測技術研究——基于牛鞭效應的視角[J].運籌與管理，2013，22(3)：53-60.

MA Yun-gao,WANG Neng-min,XU Jin-peng．Analysis of retailers’forecasting technique in supply chain-based on the bullwhip effect[J].Operations Research and Management Science，2013，22(3)：53-60.

[12]馬云高.考慮消費者價格預測影響的牛鞭效應研究[J].運籌與管理，2012，21(6)：132-137.

MA Yun-gao．Analysis of bullwhip effect under customers’ price forecasting behavior[J].Operations Research and Management Science，2012，21(6)：132-137.

[13]Zhang X L.The impact of forecasting methods on the bullwhip effect[J].International Journal of Production Economics，2004，88(1)：15-27.

[14]馬云高．基于零售商與消費者預測行為的牛鞭效應[J].系統工程，2011，29(8)：14-19.

MA Yun-gao．Bullwhip effect based on retailers and customers’forecasting behaviors[J].Systems Engineering，2011，29(8)：14-19.

[15]Wadhwa S，Bibhushan，Prakash A.Service performance of some supply chain inventory policies under demand impulses[J].Studies in Informatics and Control，2008，17(1)：43-54.

[16]尤磊，王建軍．煤炭企業供應鏈牛鞭效應模型及影響分析[J].煤炭經濟研究，2009(2)：36-39.

YOU Lei，Wang Jian-jun．Analysis of bullwhip effect model and influence in coal enterprise[J].Coal Economic Research，2009(2)：36-39.

[17]云小紅，張金鎖．基于需求模式的牛鞭效應分析[J].數學的實踐與認識，2014，45(21)：99-105.

YUN Xiao-hong，ZHANG Jin-suo．Analysis of bullwhip effect for SARMA demand model in two-level supply chain[J].Mathematics in Practices and Theory，2014，45(21)：99-105.

[18]Duc T T H，Luong H T，Kim Y.measure of bullwhip effect in a supply chain with a mixed autoregressive-moving average demand process[J].European Journal of Operational Research，2008，17(1)：43-54.

[19]Dong Won Cho，Young Hae Lee.Bullwhip effect measure in a seasonal supply chain[J].Intelligent manufacturing，2012，23：2 295-2 305.

Quantitative research on bullwhip effect in the coal supply chain

YUN Xiao-hong1，2，ZHANG Jin-suo3，JIN Hao2，4

(1.CollegeofManagement,Xi’anUniversityofScienceandTechnology,Xi’an710054,China；2.ResearchCenterforEnergyEconomicandManagement，Xi’anUniversityofScience&Technology，Xi’an710054,China；3.SchoolofEconomicsandManagement，Yan’anUniversity，Yan’an716000,China；4.CollegeofSciences,Xi’anUniversityofScienceandTechnology,Xi’an710054,China)

In the case of considering a two stage coal supply chain which is composed of a coal exploration and mining enterprise and a coal sales and transport enterprise，the coal market demand follows SARMA time series process，where the coal sales and transport enterprise uses MA technique to predict the market demand and order-up-to inventory policy to determine the coal quantity.The paper not only establishes a quantitative bullwhip effect model in two stage supply chain，but also theoretically analyzes and validates the size of the bullwhip effect including its influential factors.The research shows that：Firstly，when 0<ρ<1,0<θ<1，the bullwhip effect in the coal supply chain must happen.Then，whenL≤k≤S，the bullwhip effect is smaller.Last，the five parameters have direct effects on the bullwhip effect in the coal supply chain，such as the seasonal autoregressive coefficient，seasonal moving average coefficient，seasonal cycle，order lead time and historical data number.Specifically，the enlargement of the seasonal cycle will help to reduce the bullwhip effect，while the seasonal autoregressive coefficients is not always can reduce the bullwhip effect,the reduction of the seasonal moving average coefficients and order lead time will help to reduce the bullwhip effect.

bullwhip effect；coal supply chain；seasonality

10.13800/j.cnki.xakjdxxb.2016.0417

1672-9315(2016)04-0560-07

2015-12-27責任編輯：高佳

國家自然科學基金(71273206,71473194,71103143) ；陜西省科技廳自然科學基金(2013KJXX-40)；西安科技大學哲學社會科學繁榮發展計劃(2016SY04)

云小紅(1979-)，女，湖北隨州人，博士，講師，E-mail:yun_xiaohong@163.com

F 272

A