含三體相互作用海森堡鏈的幾何量子失諧

謝玉霞, 劉　晶

(西安郵電大學 理學院, 陜西 西安 710121)

?

含三體相互作用海森堡鏈的幾何量子失諧

謝玉霞, 劉晶

(西安郵電大學 理學院, 陜西 西安 710121)

研究含三體相互作用和外加勻強磁場時海森堡XX自旋鏈的幾何量子失諧特性，結(jié)果發(fā)現(xiàn):對有限溫度下的熱平衡態(tài)，ZZZ型三體相互作用可用來有效增強系統(tǒng)邊界量子比特之間的Bures距離量子失諧和Hellinger距離量子失諧，卻不能用來增強對應(yīng)的跡距離量子失諧;不同度量方式的幾何量子失諧會給出不同的量子態(tài)態(tài)序。

幾何量子失諧；海森堡鏈；三體相互作用

量子關(guān)聯(lián)的存在是量子系統(tǒng)區(qū)別于經(jīng)典物理系統(tǒng)的一個最顯著特征。量子糾纏一直被作為量子關(guān)聯(lián)的度量方式，是倍受關(guān)注的一個研究熱點[1]。糾纏并沒有完全刻畫出量子關(guān)聯(lián)與經(jīng)典關(guān)聯(lián)的本質(zhì)區(qū)別，如在確定性的單比特量子計算中，糾纏為零，但量子失諧卻不為零[2]。量子糾纏態(tài)都是非零量子失諧態(tài)[3]，反之則不一定成立，故量子失諧是一種比量子糾纏更廣泛的量子關(guān)聯(lián)度量方式。

當經(jīng)典互信息的兩種等價表述形式被推廣至量子系統(tǒng)時，它們不再等價，其差值可用來刻畫量子關(guān)聯(lián)的大小，由此可以得出量子失諧的度量方案[3]。從其他角度也可得出一系列不同的量子失諧度量方案，例如基于相對熵的量子失諧度量[4]和基于各種距離的幾何量子失諧度量[5-8]。

在量子信息處理任務(wù)，如遠程態(tài)制備[9]和相干操作下的信息提取[10]之中，量子失諧發(fā)揮著重要作用。相關(guān)研究涉及眾多量子力學基本問題，諸如對量子失諧的計算[11]和闡釋[12]、開放系統(tǒng)中的量子失諧魯棒性[13-17]和量子失諧保持[18]、局域操作下量子失諧的產(chǎn)生[19]和量子失諧與不確定關(guān)系[20-21]等。作為實現(xiàn)量子計算的一種潛在物理系統(tǒng)，各種自旋鏈模型的量子失諧特性[22-23]，以及量子失諧在量子相變研究中的應(yīng)用[24]也吸引著人們的關(guān)注。

本文將討論含ZZZ型三體相互作用海森堡自旋鏈邊界量子比特間的幾何量子失諧特性，并給出對應(yīng)的量子失諧調(diào)控理論方案。

1　幾何量子失諧度量

采用跡距離、Bures距離和Hellinger距離度量量子失諧，它們都是很好的幾何量子失諧度量函數(shù)[6-8]。

考慮量子態(tài)ρAB，跡距離量子失諧被定義為它和經(jīng)典-量子態(tài)集合Ω0的最小跡范數(shù)[6]，即

其中‖·‖1表示跡范數(shù)，其形式為

對于一般的量子態(tài)，DT(ρAB)的計算非常困難。但對于雙量子比特X態(tài)，其解析解為

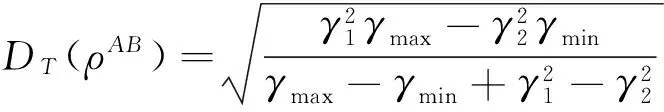
式中各參數(shù)與密度矩陣元的關(guān)系為

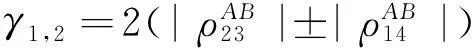
以Bures距離量子失諧[7]的定義為

其中,Ω0為經(jīng)典-量子態(tài)集合,而

為Uhlmann保真度。

對雙量子比特態(tài)ρAB，有

其中，λk為算符

按遞減順序排列的本征值，而

采用Hellinger距離的量子失諧度量，由基于密度算子的平方根所定義[8]，即

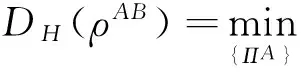
式中,{ΠA}表示作用在子系統(tǒng)A上的投影算子集合，‖·‖2表示希爾伯特-施密特范數(shù)。

對雙量子比特態(tài)ρAB，DH(ρAB)可簡化為[25]

DH(ρAB)=1-λmax(W)。

其中,λmax(W)表示矩陣W的最大特征值。矩陣W的各元素為

2　理論模型

考慮含ZZZ型三體相互作用的開邊界海森堡XX自旋鏈，對應(yīng)的系統(tǒng)哈密頓量為[26]

式中,J表示相鄰自旋格點之間的交換耦合作用強度，B表示沿z軸方向所加的勻強外磁場，α表示三體相互作用的強度。

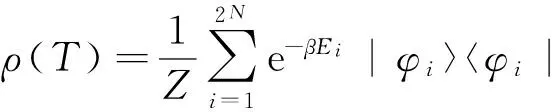
其中,Z為配分函數(shù)，且

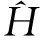
在很多量子信息處理任務(wù)中，邊界量子比特之間的量子關(guān)聯(lián)起著決定性作用，故以下僅考察系統(tǒng)邊界量子比特間的幾何量子失諧特性，并把兩端的自旋格點分別稱為量子比特A和B，對應(yīng)的密度算子記為

ρAB=tr2,…,N-1ρ(T)。

3　結(jié)果和討論

不同量子關(guān)聯(lián)度量函數(shù)具有不同系統(tǒng)參數(shù)依賴特性。在此主要考察海森堡自旋鏈中的跡距離、Bures距離和Hellinger距離量子失諧特性，以期找出最佳參數(shù)區(qū)間，實現(xiàn)系統(tǒng)熱平衡態(tài)量子關(guān)聯(lián)的有效調(diào)控。

考察ZZZ型三體相互作用對系統(tǒng)邊界量子比特間跡距離量子失諧的影響。DT(ρAB)對α的依賴關(guān)系如圖1所示。其中,重標溫度kBT=0.5，磁場強度分別為B=0和B=2,從上到下各條曲線依次對應(yīng)量子比特數(shù)N=3,4,…,9。可見，當沒有外加磁場時，對于三量子比特熱平衡態(tài)的特殊情形，DT(ρAB)始終保持常數(shù)值0.493，而對于其他數(shù)目量子比特的情形，DT(ρAB)則隨著α的增大而單調(diào)減小。當給系統(tǒng)加上沿z軸方向的勻強外磁場時，DT(ρAB)均隨著α的增大而減小，并且減小的速度要快于沒有外加磁場時的情形。這意味著,ZZZ型三體相互作用不能用來增強海森堡XX自旋鏈邊界量子比特之間的跡距離量子失諧。

圖1　DT(ρAB)對α的依賴關(guān)系

考察Bures距離量子失諧對ZZZ型三體相互作用強度的依賴關(guān)系。相關(guān)數(shù)值模擬結(jié)果如圖2所示。其中kBT=0.5，B=0或B=2,從上到下各條曲線依次對應(yīng)量子比特數(shù)N=3,4,…,9。可見，和跡距離量子失諧不同的是，當沒有外磁場時，三量子比特態(tài)的DB(ρAB)隨著α的增大而單調(diào)的趨近于其穩(wěn)態(tài)平衡值0.5;對其他情形,DB(ρAB)則在三體相互作用相對較弱的區(qū)間內(nèi)得到了某種程度的增大。不同總數(shù)目量子比特熱平衡態(tài)所對應(yīng)DB(ρAB)的增幅并不相同:對圖2(a)所選擇的系統(tǒng)參數(shù)，增幅介于5.6% ～24.8%;給系統(tǒng)加上沿z軸方向的外磁場后，如圖2(b)所示，DB(ρAB)轉(zhuǎn)而隨著α的增大而單調(diào)衰減。這說明，對所考慮的自旋鏈模型，外加磁場也不利于Bures距離量子失諧的提升。

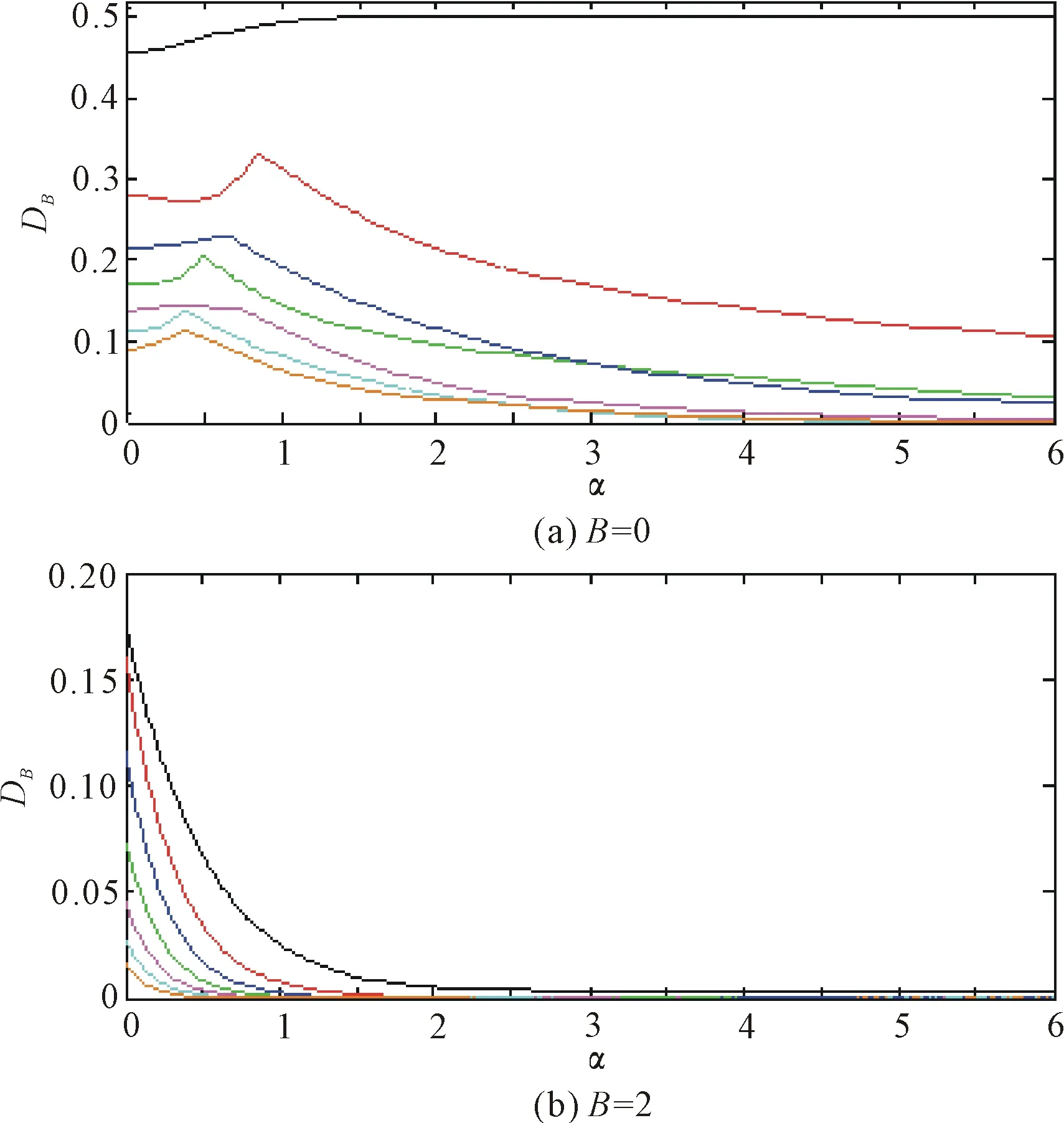
圖2　DB(ρAB)對α的依賴關(guān)系

考察ZZZ型三體相互作用對系統(tǒng)邊界量子比特間Hellinger距離量子失諧的影響。取kBT=0.5，B=0或B=2，所得數(shù)值模擬結(jié)果如圖3所示，從上到下各條曲線依次對應(yīng)的總量子比特數(shù)為N=3,4,…,9。由此可見，DH(ρAB)在定性上表現(xiàn)出和DB(ρAB)類似的對α依賴關(guān)系，即不加外磁場時，DH(ρAB)可以通過引入ZZZ型三體相互作用而得到較為明顯的增強。對圖3(a)中選定的系統(tǒng)參數(shù)，不同數(shù)目量子比特熱平衡態(tài)所對應(yīng)DH(ρAB)的增幅介于10.7%～76.4%。從圖3(b)也可以發(fā)現(xiàn)外磁場的加入不利于Hellinger距離量子失諧的提升。

圖3　DH(ρAB)對α的依賴關(guān)系

綜上可知,不同幾何量子失諧度量會給出不同的量子態(tài)態(tài)序。在沒有外加磁場時，除三量子比特情形，隨著三體相互作用的增強，跡距離量子失諧總是單調(diào)的減小，而Bures距離和Hellinger距離量子失諧則會出現(xiàn)一個或兩個峰值。實際上，不同量子失諧度量函數(shù)會給出不同態(tài)序的現(xiàn)象，在研究量子關(guān)聯(lián)動力學問題中也已被發(fā)現(xiàn)[14]。

4　結(jié)語

利用跡距離、Bures距離和Hellinger距離量子失諧的概念，研究了含ZZZ型三體相互作用海森堡鏈的量子關(guān)聯(lián)調(diào)控問題。結(jié)果表明：對有限溫度下的系統(tǒng)熱平衡態(tài)，ZZZ型三體相互作用可作為一種有效的系統(tǒng)參數(shù)，來增強系統(tǒng)邊界量子比特之間的Bures距離量子失諧和Hellinger距離量子失諧，但不能用來增強對應(yīng)的跡距離量子失諧；給系統(tǒng)加上沿z軸方向的勻強外磁場，也不利于所考慮各種幾何量子失諧的增強；另外，不同度量方式的幾何量子失諧會給出不同的量子態(tài)態(tài)序。

[1]HORODECKI R, HORODECKI P, HORODECKI M, et al. Quantum entanglement[J/OL]. Reviews of Modern Physics, 2007, 81(2): 865-942[2016-03-03].https://www.researchgate.net/publication/2200779_Quantum_Entanglement.DOI: 10.1103/ RevModPhys.81.865.

[2]DATTA A, SHAJI A, CAVES C M. Quantum discord and the power of one qubit[J/OL]. Physical Review Letters, 2008, 100(5):050502[2016-03-03].http://physics.unm.edu/CQuIC/pubs/pubswiki/images/e/ed/Datta08a.pdf.DOI: 10.1103/PhysRevLett.100.050502.

[3]OLLIVIER H, ZUREK W H. Quantum discord: a measure of the quantumness of correlations[J/OL]. Physical Review Letters, 2002, 88(1): 017901[2016-03-03].http://arxiv.org/pdf/quant-ph/0105072v3.DOI: 10.1103/PhysRevLett.88.017901.

[4]MODI K, PATEREK T, SON W, et al. Unified view of quantum and classical correlations[J/OL]. Physical Review Letters, 2010, 104(8):080501[2016-03-03].http://www.arxiv.org/pdf/0911.5417.pdf.DOI: 10.1103/ PhysRevLett.104. 080501.

[5]DAKIC B, VEDRAL V, BRUKNER C. Necessary and sufficient condition for nonzero quantum discord[J/OL]. Physical Review Letters, 2010, 105(19):190502[2016-03-03].http://www.arxiv.org/pdf/1004.0190.pdf.DOI: 10.1103/ PhysRevLett.105.190502.

[6]PAULA F M, OLIVEIRA T R, SARANDY M S. Geometric quantum discord through the Schatten 1-norm[J/OL]. Physical Review A, 2013, 87(6): 064101[2016-03-03].http://arxiv.org/pdf/1302.7034v1.DOI: 10.1103/PhysRevA.87. 064101.

[7]SPEHNER D, ORSZAG M. Geometric quantum discord with Bures distance[J/OL]. New Journal of Physics, 2013, 15(10):103001[2016-03-03].http://dx.doi.org/10.1088/1367-2630/15/10/103001.

[8]CHANG L, LUO L. Remedying the local ancilla problem with geometric discord[J/OL]. Physical Review A, 2013, 87(6):062303[2016-03-03].http://dx.doi.org/10.1103/PhysRevA.87.062303.

[9]GU M, CHRZANOWSKI H M, ASSAD S M, et al. Observing the operational significance of discord consumption[J/OL]. Nature Physics, 2012, 8(9): 671-675[2016-03-03].http://www.arxiv.org/pdf/1203.0011.pdf.DOI: 10.1038/NPHYS2376.

[10] DAKIC B, LIPP Y O, MA X, et al. Quantum discord as resource for remote state preparation[J/OL]. Nature Physics, 2012, 8(9): 666-670[2016-03-03].http://arxiv.org/abs/1203.1629.DOI: 10.1038/NPHYS2377.

[11] LUO S L. Quantum discord for two-qubit systems[J/OL]. Physical Review A, 2008, 77(4): 042303[2016-03-03].http://pra.aps.org/abstract/PRA/v77/i4/e042303.DOI: 10.1103/PhysRevA.77.042303.

[12] MADHOK V, DATTA A. Interpreting quantum discord through quantum state merging[J/OL]. Physical Review A, 2011, 83(3):032323[2016-03-03].http://www.arxiv.org/pdf/1008.4135.pdf.DOI: 10.1103/PhysRevA.83.032323.

[13] MAZZOLA L, PILLO J, MANISCALCO S. Sudden transition between classical and quantum decoherence[J/OL]. Physical Review Letters, 2010, 104(20): 200401[2016-03-03].http://core.ac.uk/download/pdf/29084590.pdf.DOI: 10.1103/ PhysRevLett.104. 200401.

[14] HU M L, FAN H. Robustness of quantum correlations against decoherence[J/OL]. Annals of Physics, 2011, 327(3): 851-860[2016-03-03].http://arxiv.org/pdf/1111.2646.DOI: 10.1016/ j.aop.2011.11.001.

[15] WANG B, XU Z Y, CHEN Z Q, et al. Non-Markovian effect on the quantum discord[J/OL]. Physical Review A, 2009, 81(1): 014101[2016-03-03].http://arxiv.org/PS_cache/arxiv/pdf/0911/0911.1845v1.pdf.DOI: 10.1103/PhysRevA.81.014101.

[16] HU M L, FAN H. Evolution equation for geometric quantum correlation measures[J/OL]. Physical Review A, 2015, 91(5): 052311[2016-03-03].http://link.aps.org/doi/10.1103/PhysRevA.91.052311.

[17] HU M L, FAN H. Dynamics of entropic measurement-induced nonlocality in structured reservoirs[J/OL]. Annals of Physics, 2012, 327(9): 2343-2353[2016-03-03].http://dx.doi.org/10.1016/j.aop.2012.04.003.

[18] HU M L, TIAN D P. Preservation of the geometric quantum discord in noisy environments[J/OL]. Annals of Physics, 2014, 343(4): 132-140[2016-03-03].http://dx.doi.org/10.1016/j.aop.2014.02.003.

[19] HU X, FAN H, ZHOU D L, et al. Necessary and sufficient conditions for local creation of quantum correlation[J/OL]. Physical Review A, 2011, 85(3):032102[2016-03-03].http://theory.iphy.ac.cn/English/paper/PhysRevA.85.032102.pdf.DOI: 10.1103/PhysRevA.85.032102.

[20] HU M L, FAN H. Competition between quantum correlations in the quantum-memory-assisted entropic uncertainty relation[J/OL]. Physical Review A, 2013, 87(2):022314[2016-03-03]. http://xxx.tau.ac.il/pdf/1212.0319v1.DOI: 10.1103/ PhysRevA.87.022314.

[21] HU M L, FAN H. Upper bound and shareability of quantum discord based on entropic uncertainty relations[J/OL]. Physical Review A, 2013, 88(1): 014105[2016-03-03].http://www.oalib.com/paper/3646621.DOI: 10.1103/PhysRevA.88.014105.

[22] CILIBERTI L, ROSSIGOLI R, CANOSA N. Quantum discord in finite XY chains[J/OL]. Physical Review A, 2010, 82(4): 042316[2016-03-03].http://arxiv.org/pdf/1105.0027v1.DOI: 10.1103/PhysRevA.82.042316.

[23] WANG C, ZHANG Y Y, CHEN Q H. Quantum correlations in collective spin systems[J/OL]. Physical Review A, 2012, 85(5): 052112[2016-03-03].http://www.arxiv.org/pdf/1202.4324.pdf.DOI: 10.1103/ PhysRevA.85.052112.

[24] WERLANG T, TRIPPE C, RIBEIRO G A, et al. Quantum correlations in spin chains at finite temperatures and quantum phase transitions[J/OL]. Physical Review Letters, 2010, 105(9):095702[2016-03-03].http://www.arxiv.org/pdf/1006.3332.pdf.DOI: 10.1103/PhysRevLett.105.095702.

[25] GIROLAMI D, TUFARELLI T, ADESSO G. Characterizing nonclassical correlations via local quantum uncertainty[J/OL]. Physical Review Letters, 2012, 110(24):240402[2016-03-03].http://arxiv.org/pdf/1212.2214v5.DOI: 10.1103/PhysRevLett.110.240402.

[26] PACHOS J K, PLENIO M B. Three-spin interactions in optical lattices and criticality in cluster Hamiltonians[J/OL]. Physical Review Letters, 2004, 93(5): 056402[2016-03-03].http://cds.cern.ch/record/706719/files/0401106.pdf.DOI: 10.1103/ PhysRevLett.93.056402.

[責任編輯:瑞金]

Geometric quantum discords in the Heisenberg chain with three-site interaction

XIE Yuxia,LIU Jing

(School of Science, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)

Properties of various geometric quantum discords in the Heisenberg XX spin chain with three-site interactions and external magnetic fields is investigated. The results show that for thermal states of the system at finite temperature, the ZZZ type three-site interaction can be used to enhance evidently the Bures distance discord and the Hellinger distance discord, while the trace distance discord can only be decreased. Moreover, different measures of geometric quantum discords can impose different orderings of quantum states.

Geometric quantum discord, Heisenberg chain, three-site interaction

10.13682/j.issn.2095-6533.2016.04.016

2016-05-05

陜西省自然科學基礎(chǔ)研究計劃資助項目(2014JM1008)

謝玉霞(1980-)，女，碩士，助教，從事量子通信理論研究。E-mail: yuxia1124@163.com

劉晶(1980-)，女，碩士，講師，從事數(shù)值計算研究。E-mail: xingxin909@126.com

TN918; O431

A

2095-6533(2016)04-0083-05