一維雙極量子能量輸運穩態模型弱解的存在性

董建偉， 程春蕊， 王艷萍

(鄭州航空工業管理學院 理學院， 河南 鄭州 450015)

?

一維雙極量子能量輸運穩態模型弱解的存在性

董建偉， 程春蕊， 王艷萍

(鄭州航空工業管理學院 理學院， 河南 鄭州 450015)

在一維有界區域上研究一個半導體雙極量子能量輸運穩態模型.將此模型變形為由2個四階橢圓方程和1個二階退化橢圓方程組成的耦合方程組.利用截斷方法和Leray-Schauder不動點定理證明了其變形后方程組弱解的存在性.

量子能量輸運模型；穩態解；存在性

Journal of Zhejiang University(Science Edition), 2016,43(5):521-524

量子漂移擴散模型、量子能量輸運模型和量子流體動力學模型為半導體器件中常見的三大宏觀量子模型.通過宏觀量，例如電子密度、空穴密度、電流密度、粒子溫度和電位勢描述半導體器件中的載流子運動規律.最近，JUNGEL等[1]從完整的量子流體動力學模型中推導出簡化的量子能量輸運模型：

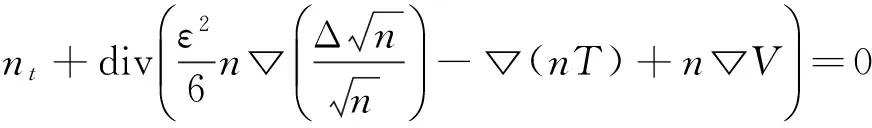
(1)

-div(n▽T)=n(TL(x)-T)，

(2)

ΔV=n-C(x)，

(3)

其中，電子密度n、電子溫度T和電位勢V為未知函數，晶格溫度TL(x)和雜質密度C(x)為已知函數，普朗克常數ε>0為物理參數.在周期邊界條件下，文獻[1]首先證明了式(1)～(3)弱解的整體存在性，后來文獻[2]研究了其解的半古典極限狀態(ε→0).最近，文獻[3]證明了式(1)～(3)的一維穩態模型古典解的存在性.關于式(1)～(3)不帶量子項(即ε=0)的經典能量輸運模型方面的研究結果見文獻[4-5].當T=TL(x)=常數時，式(1)～(3)即變為量子漂移-擴散模型，近幾年對此類模型已有大量研究成果[6-15].

1　主要結果

在一維有界區域(0,1)上研究式(1)～(3)的雙極穩態模型：

(4)

(5)

-((n+p)Tx)x=(n+p)(TL(x)-T),

(6)

Vxx=n-p-C(x)，x∈(0,1)，

(7)

n(0)=n(1)=1,p(0)=p(1)=1，

(8)

nx(0)=nx(1)=px(0)=px(1)=

Tx(0)=Tx(1)=0,

(9)

其中電子密度n、空穴密度p、粒子溫度T和電位勢V為未知函數，晶格溫度TL(x)和雜質密度C(x)為已知函數，常數J1,J2分別表示電子電流密度和空穴電流密度.

式(4)、(5)分別除以n,p，再關于x求導，并利用式(7)得

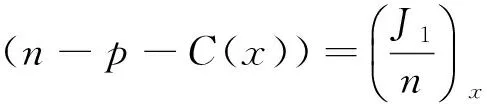
(10)

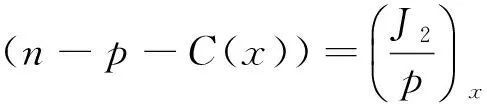
(11)

令n=eu，p=ev，則式(10),(11),(6),(8),(9)相應變為

(eu-ev-C(x))=J1(e-u)x，

(12)

(eu-ev-C(x))=J2(e-v)x，

(13)

-((eu+ev)Tx)x=(eu+ev)(TL(x)-T),

(14)

u(0)=u(1)=0,v(0)=v(1)=0,

(15)

ux(0)=ux(1)=vx(0)=vx(1)=

Tx(0)=Tx(1)=0.

(16)

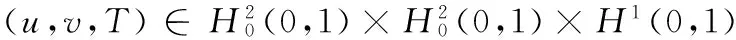
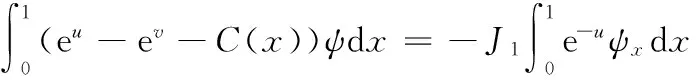
(17)

(18)

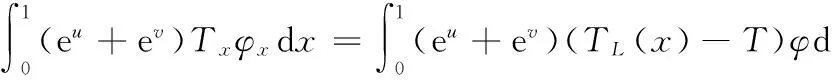
(19)

本文的主要結果為：

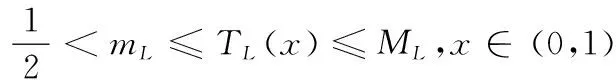
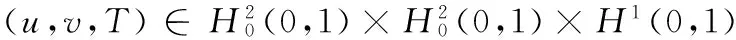
2　定理1的證明

先考慮式(17)、(18)和如下截斷問題：

(20)

其中,uM=min{M,max{-M,u}}，常數M的定義見后文的式(25)，vM的定義與uM類似.

(21)

另外，有

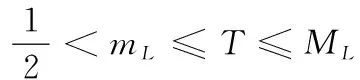
(22)

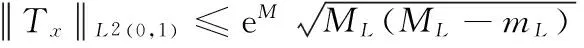
(23)

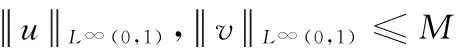
(24)

其中，

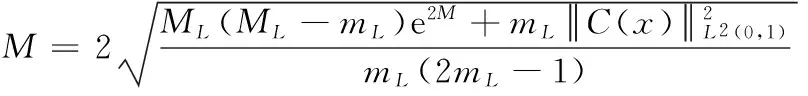
(25)

證明用φ=(T-ML)+=max{0,T-ML}∈H1(0,1)作為式(20)的試驗函數，得

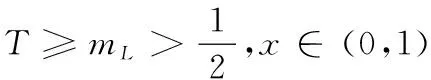
用φ=T∈H1(0,1)作為式(20)的試驗函數，得

2eM(ML-mL)ML，

所以式(23)成立.

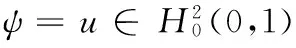
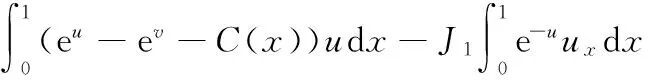
(26)

由Young不等式及式(23)，可以估計式(26)的右端第1項：

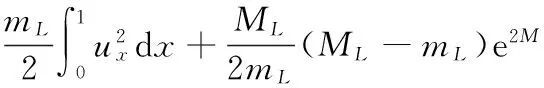
又因為

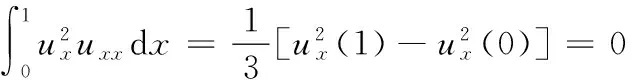
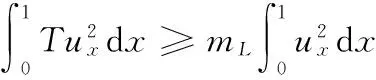
所以由式(26)可得

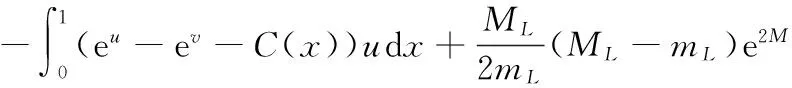
(27)

(28)

式(27)與(28)兩邊分別相加，得

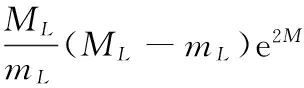
(29)

由Young及Poincare不等式知，

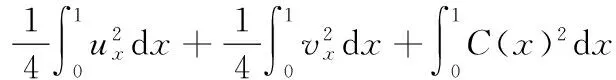
又因為

所以由式(29)可推得式(21).

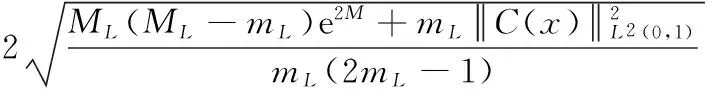
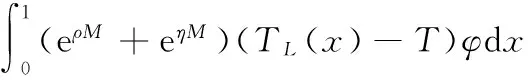
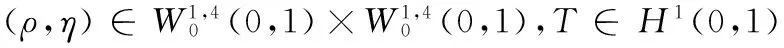
(30)

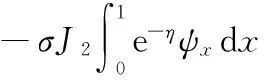
(31)

其中，σ∈[0,1]，定義雙線性形式

(32)

線性泛函

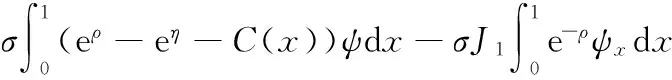
[1]JUNGEL A, MILISIC J P. A simplified quantum energy-transport model for semiconductors[J]. Nonlinear Analysis: Real World Applications, 2011,12(2):1033-1046.

[2]CHEN L, CHEN X Q, JUNGEL A. Semiclassical limit in a simplified quantum energy-transport model for semiconductors [J]. Kinetic and Related Models,2011,4(4):1049-1062.

[3]DONG J W, ZHANG Y L, CHENG S H. Existence of classical solutions to a stationary simplified quantum energy-transport model in 1-dimensional space[J]. Chinese Annals of Mathematics： Ser B, 2013,34(5):691-696.

[4]JUNGEL A, PINNAU R, ROHRIG E. Existence analysis for a simplified energy-transport model for semiconductors [J]. Math Meth Appl Sci,2013,36(13):1701-1712.

[5]董建偉，琚強昌.一個一維半導體簡化能量輸運模型的穩態解[J].數學年刊：A輯,2014,35(5):613-622.

DONG Jianwei, JU Qiangchang. A stationary solution to a 1-dimensional simplified energy-transport model

for semiconductors[J]. Chinese Annals of Mathematics： SerA,2014,35(5):613-622.

[6]JUNGEL A, VIOLET I. The quasi neutral limit in the quantum drift-diffusion equations [J]. Asymptotic Analysis,2007,53(3):139-157.

[7]CHEN L, JU Q C. Existence of weak solution and semiclassical limit for quantum drift-diffusion model[J]. Z Angew Math Phys,2007,58(1):1-15.

[8]CHEN X Q. The global existence and semiclassical limit of weak solutions to multidi-mensional quantum drift-diffusion model[J]. Advanced Nonlinear Studies,2007,7(1):651-670.

[9]CHEN X Q, CHEN L, JIAN H Y. The dirichlet problem of the quantum drift-diffusion model[J]. Nonlinear Analysis,2008,69(9):3084-3092.

[10]CHEN X Q, CHEN L. Initial time layer problem for quantum drift-diffusion model[J]. J Math Anal Appl,2008,343(1):64-80.

[11]CHEN X Q, CHEN L, JIAN H Y. Existence, semiclassical limit and long-time behavior of weak solution to quantum drift-diffusion model[J]. Nonlinear Analysis: Real World Applications, 2009,10(3):1321-1342.

[12]CHEN X Q. The isentropic quantum drift-diffusion model in two or three space dimensions[J]. Z Angew Math Phys,2009,60(3):416-437.

[13]NISHIBATA S, SHIGETA N, SUZUKI M. Asymptotic behaviors and classical limits of solutions to a quantum drift-diffusion model for semiconductors [J]. Mathematical Models and Methods in Applied Sciences,2010,20(6):909-936.

[14]DONG J W. Classical solutions to the one-dimensional stationary quantum drift-diffusion model[J]. Journal of Mathematical Analysis and Applications,2013,399(2):594-598.

[15]董建偉，張偉.關于一維穩態量子漂移-擴散模型[J].數學進展，2015,44(2):263-270.

DONG Jianwei, ZHANG Wei. On the stationary quantum drift-diffusion model in one space dimension [J]. Advances in Mathematics,2015,44(2):263-270.

Existence of weak solutions to a stationary 1-dimensional bipolar quantum energy-transport model.

DONG Jianwei, CHENG Chunrui, WANG Yanping

(SchoolofMathematicsandPhysics,ZhengzhouInstituteofAeronauticalIndustryManagement,Zhengzhou450015,China)

A stationary bipolar quantum energy-transport model for semiconductors is studied in a 1-dimensional bounded domain. The model is reformulated as a coupled system consisting of two fourth-order elliptic equations and a second-order degenerate elliptic equation. The existence of weak solutions to the reformulated system is proved using the truncation method and the Leray-Schauder fixed-point theorem.

quantum energy-transport model; stationary solutions; existence

2015-10-15.

河南省科技廳基礎與前沿技術研究計劃項目 (162300410077)；航空科學基金項目(2013ZD55006)；河南省高等學校青年骨干教師資助計劃項目(2013GGJS-142)；鄭州航空工業管理學院青年科研基金項目(2013111001，2014113002，2015113001).

董建偉(1980-)，ORCID:http//orcid.org/0000-0003-1131-8244，男，碩士，副教授，主要從事偏微分方程研究，E-mail:dongjianweiccm@163.com.

10.3785/j.issn.1008-9497.2016.05.004

O 175.2

A

1008-9497(2016)05-521-04