基于EMMS模型的氣固鼓泡床的模擬及氣泡特性的分析

吳迎亞，彭麗，高金森，藍興英

（中國石油大學（北京）重質油國家重點實驗室，北京 102249）

基于EMMS模型的氣固鼓泡床的模擬及氣泡特性的分析

吳迎亞，彭麗，高金森，藍興英

（中國石油大學（北京）重質油國家重點實驗室，北京 102249）

基于EMMS曳力模型，采用雙流體的方法對氣固鼓泡床內的氣固流動特性進行模擬，建立基于圖像處理氣泡特性的分析方法，重點研究了不同表觀氣速下氣泡在床層內分布特性，包括氣泡平均當量直徑、氣泡速度和氣泡球形度的軸向分布，以及氣泡的生命周期。研究結果表明，小氣泡多集中在床層底部和壁面區域，而大氣泡多集中在床層中間區域。隨著表觀氣速的增加，床層高度不斷增加，氣泡的球形度降低，氣泡的大小、出現頻率、上升速度以及生命周期均增加；然而，當表觀氣速增大到一定程度，繼續增加氣速對氣泡的上升速度影響不大。

氣固鼓泡床；多相流；計算流體力學；TFM；EMMS；氣泡

引　言

氣固鼓泡床具有良好的混合、傳熱及傳質效果，在過程工業中有著廣泛的應用［1］。計算流體力學方法（CFD）［2］被廣泛應用于研究鼓泡床內氣固流動行為的研究，其中歐拉-歐拉雙流體模型（TFM）的應用最為廣泛。雙流體模型將氣相和顆粒相均看成連續介質，滿足質量、動量和能量守恒方程，其中顆粒相的壓力、黏度等物性采用顆粒動理學（KTGF）描述，氣固相間相互作用采用曳力模型描述［3-4］。而對于FCC這類Geladart A類顆粒而言，在流動過程中極易發生團聚現象，造成體系內較大顆粒聚團的生成，從而使得曳力降低。因此，采用Gidaspow等［5-8］經典曳力模型難以準確地模擬FCC顆粒在鼓泡床內的氣固流動現象，高估了床層的膨脹率［9-12］。為此，很多研究者對曳力模型進行修正，其中應用最廣泛的是能量最小化多尺度（EMMS）曳力模型［13］。研究者采用雙流體模型耦合 EMMS曳力模型模擬氣固循環流化床內氣固流動特性［14-16］，研究結果發現，采用EMMS曳力模型能較好地模擬出氣固循環流化床內的氣固流動特性［17-21］。Shi等［22］進一步將應用于氣固循環流化床模擬中的 EMMS曳力模型拓展并應用于氣固鼓泡床的數值模擬，發展了新的基于氣泡修正的EMMS曳力模型，并能較為準確地預測鼓泡床內的床層膨脹率等特性。此外，氣固鼓泡床內氣泡和顆粒之間存在著強烈的作用，加強了鼓泡床內氣固的接觸效率，保證了其良好的傳熱、傳質以及反應特性。眾多研究者通過實驗和模擬研究發現［23-26］，鼓泡床內氣泡的分布和顆粒的循環方式是相互影響的：氣泡和顆粒的返混決定了氣固的反應特性；氣泡的大小、形態及運動規律決定了氣固傳熱傳質特性。因此，研究鼓泡床內氣泡分布和氣泡運動規律對進一步認識鼓泡床內的氣固流動、傳熱及傳質機制有著重要的意義。而前人的研究［23-26］工作中一般只關注了氣泡的平均性質，而對氣泡在床層內的瞬時分布特性以及氣泡的動態變化過程缺乏深入研究。本文首先基于EMMS曳力模型分析了鼓泡床內的氣固流動特性，并在此基礎上建立了識別氣泡和分析氣泡的方法，分析了鼓泡床內氣泡的平均性質、氣泡在床層內的整體分布特性以及氣泡的生命周期。

1　模擬對象

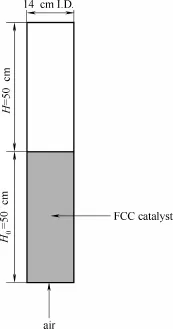
圖1　模擬對象的幾何結構［9］Fig. 1　Geometry structure of simulation domain［9］

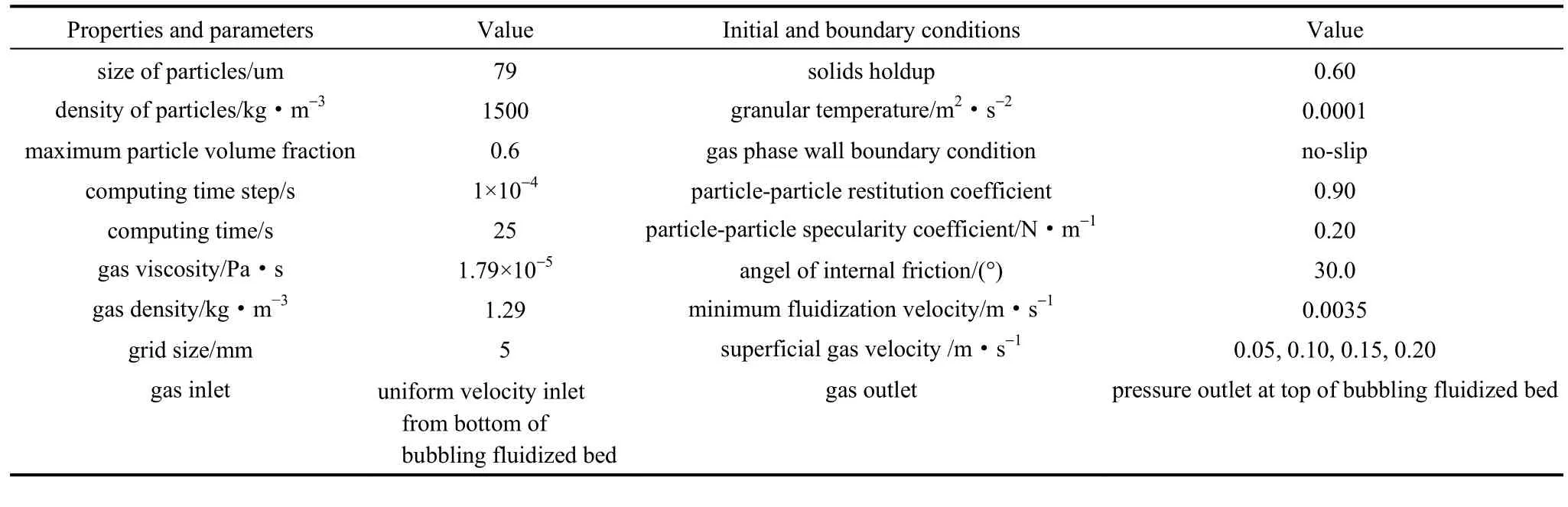
表1　模擬條件Table 1　Simulation conditions

本文的模擬工況為M cKeen等［9］建立的三維柱形氣固鼓泡床冷態實驗。模擬對象如圖1所示，具體的實驗條件及相關參數如表1所示。在室溫下進行了4個表觀氣速（0.05、0.10、0.15、0.20 m·s-1）的實驗。雖然三維模擬能更加準確地反映出氣固體系的復雜流動特性，但是考慮到計算能力的限制，二維模擬作為一種較為準確和經濟的簡化方法，被眾多研究者采用［21，27-28］。因此，本文在模擬計算過程中采用二維模擬，計算時間步長為0.001 s，氣體流經整個床層需要的時間約為5 s，為了取得較穩定的床層，共模擬了鼓泡床流動時間為25 s。在下文后續分析中，除床層以及氣泡的瞬時特性外，床層內顆粒體積分數分布和氣泡的平均性質的分析均取5～25 s之間的平均數據。進行網格無關性研究后，發現軸向和徑向上采用5 mm × 5 mm的均勻網格滿足計算需求。因此，本模擬選擇的網格尺寸為 5 mm × 5 mm的均勻網格。

表2　模型的控制方程Table 2　Governing equations

2　雙流體模型

本文采用歐拉雙流體方法（TFM）結合顆粒動理學理論（KTGF）對氣固鼓泡床進行模擬研究，模型的控制方程組如表2所示，關于模型的本構方程及相關表達式見文獻［29］。

表3　不同表觀氣速下的曳力模型Table 3　Correction factor for different superficial gas velocity

圖2　氣泡的表征方法Fig. 2　Method of bubble characterization

氣固之間的曳力模型采用EMMS曳力模型［22］。EMMS曳力模型是在Wen-Yu曳力模型的基礎上修正得到。其曳力系數表達式如下

其中f為修正因子［22］，不同氣速下修正因子如表3所示。

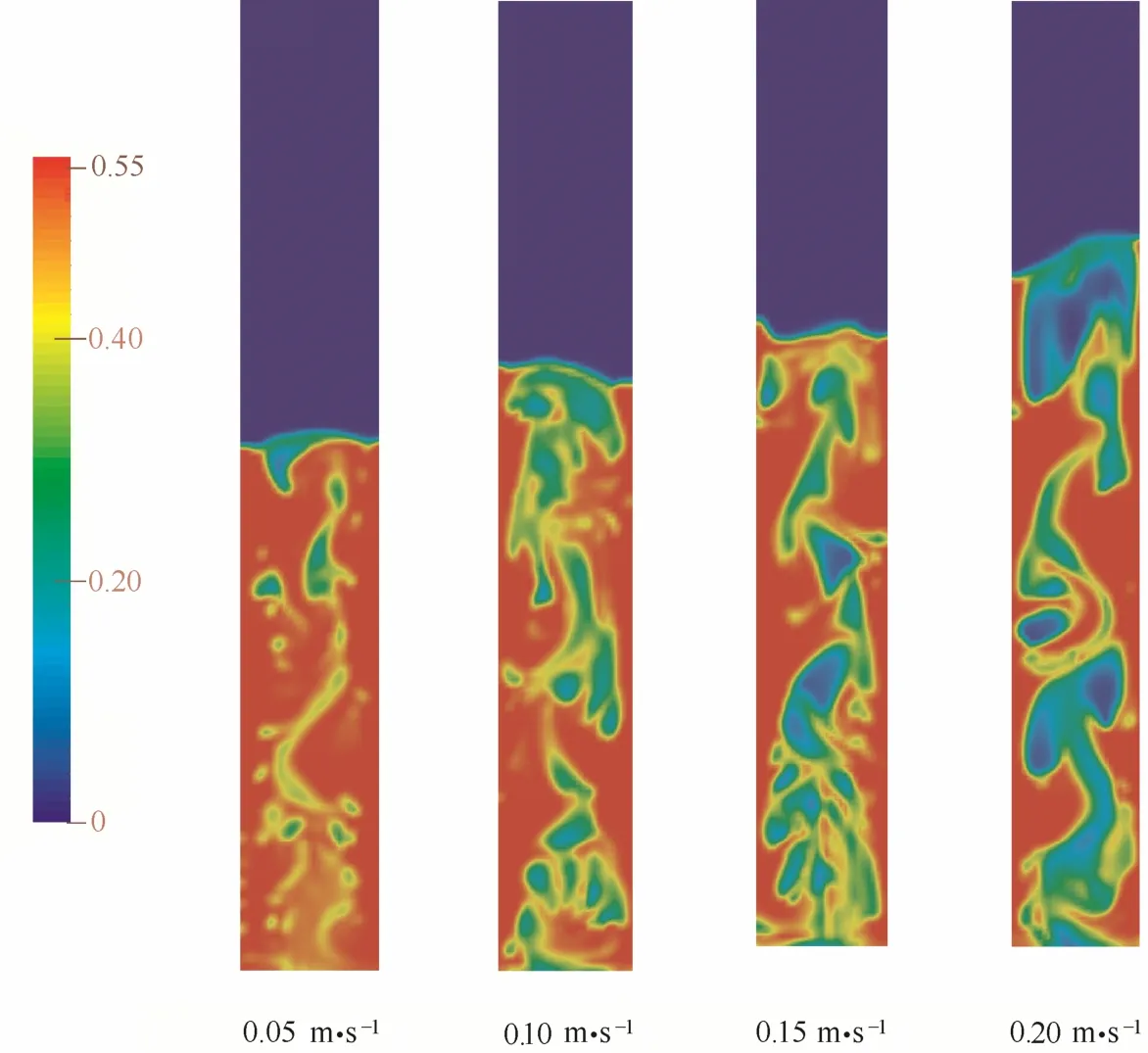
圖3　不同表觀氣速下床層內顆粒體積分數瞬時分布云圖（10 s）Fig. 3　Instantaneous profiles of solids volume fraction at different superficial gas velocity at 10 s

3　結果與討論

3.1氣泡分析方法

為了研究鼓泡床內的氣泡特征，本研究基于模擬得到的鼓泡床內氣含率分布云圖建立識別和分析氣泡的方法，如圖2所示。具體步驟如下：① 通過選擇一個合適的氣含率閾值識別和提取氣泡［23-26］（一般定義鼓泡床中固含率小于 0.2的區域為氣泡）；② 根據所選定的閾值將模擬得到的鼓泡床內氣含率分布云圖二值化；③ 通過邊緣檢測算法，確定氣泡的邊緣；④ 計算出氣泡的中心位置和面積；⑤ 對相鄰幀的氣泡進行對比分析，求取氣泡運動的速度。此外，為了進一步表征氣泡的特征，對氣泡進行球形近似，通過氣泡的當量直徑和球形度表征氣泡的特性。其定義如下

其中C為球形度，A為氣泡的面積，S為氣泡的周長。C越接近于1，表示氣泡接近完美球形。

3.2氣固流動特性

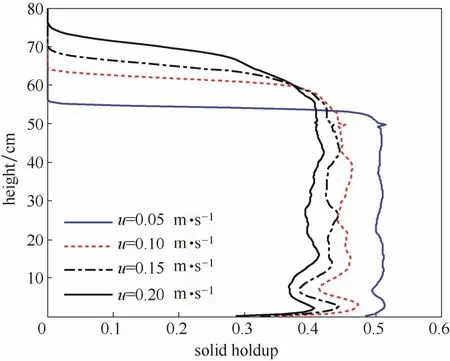
圖4　不同表觀氣速下時均顆粒體積分數的軸向分布（5～25 s）Fig. 4　Axial profiles of time-averaged solids volume fraction under different superficial gas velocity at 5—25 s

圖3為模擬得到的不同表觀氣速下床層顆粒體積分數在模擬時間為10 s的瞬時分布云圖。圖4為不同表觀氣速下床層時均顆粒體積分數的軸向分布圖。由圖3和圖4可知，隨著表觀氣速的增大，床層高度不斷增加；在床層高度為0～50 cm內，床層內的顆粒體積分數隨表觀氣速的增加不斷降低；同時沿床層高度方向，氣泡的大小也明顯變大。在較低氣速下（0.05 m·s-1），床層界面清晰；而在較高氣速下（0.20 m·s-1），床層界面有較大波動。表4對比了不同表觀氣速下床層高度的模擬結果和實驗數據［9］。由表 4可知，模擬計算值略高于實驗值，這可能是由于模擬計算中忽略了多孔型分布板和電容層析成像裝置的影響，造成了模擬值偏高。

圖5　不同表觀氣速下時均顆粒體積分數的徑向分布（5～25 s）Fig. 5　Radial profiles of time-averaged solids volume fraction under different superficial gas velocity at 5—25 s

表4　不同表觀氣速下床層高度的模擬結果和實驗結果對比Table 4　Height in simulation and experiment under different superficial gas velocity

圖6　不同表觀氣速下時均顆粒速度的徑向分布（5～25 s）Fig. 6　Radial profiles of time-averaged solids velocity under different superficial gas velocity at 5—25 s

圖5和圖6分別為不同表觀氣速下床層時均顆粒體積分數和顆粒速度在床高H = 12、28和42 cm處的徑向分布。從圖5可以看出，在床層的不同高度截面處，顆粒體積分數沿徑向均呈現中間低邊壁高的不均勻分布規律，由中心到邊壁，分布曲線變陡，顆粒體積分數變大，在壁面處達到最大值。在較低氣速下，顆粒體積分數較高，而且在徑向上分布較為均勻；在較高氣速下，中心處呈現較低的波谷，且氣速越大波谷越低。同一氣速下，在床層的不同高度截面處，顆粒體積分數分布情況變化不大。由圖6可以看出，在床層的不同高度截面處，均呈現出床層中心區域顆粒速度大，邊壁區域顆粒速度小的分布趨勢，且隨著氣速的增大，床層中心區域的顆粒速度不斷增加。

3.3氣泡特征

氣泡在鼓泡床中有極其重要的作用，氣泡的生成、聚并以及破碎決定了氣固鼓泡床的傳熱和反應效率。在準確模擬鼓泡床內氣固流動特性的基礎上，采用基于圖像處理氣泡的分析方法（見3.1節），進一步分析了氣固鼓泡床內的氣泡特性。

圖7為不同表觀氣速下，鼓泡床內氣泡平均當量直徑的軸向分布。由圖7可知，隨著床層高度的增加，氣泡逐漸增大。在較低的氣速下（0.05 m·s-1和 0.10 m·s-1），當床層高度增加到一定程度，氣泡大小趨于穩定，停止生長，直至在氣固相界面發生破碎。在較高的氣速下（0.15 m·s-1和 0.20 m·s-1），由于氣體表觀速度較大，氣固之間的湍動激烈，隨著床層高度的增加，氣泡的大小總體趨于增大的趨勢，但是由于激烈的湍動，造成一定的波動。圖8是不同表觀氣速下，氣泡平均上升速度的軸向分布。總體上來說，隨著床層高度的增加，氣泡上升速度增加。然而，當表觀氣速增大到一定程度，繼續增大表觀氣速對氣泡上升速度的影響不大。圖9是不同表觀氣速下，鼓泡床內氣泡的球形度的軸向分布。由圖9可以發現，在較低氣速下，氣泡較小，球形度較大；在較高氣速下，氣泡較大，球形度較小。這是由于氣固之間強烈的湍動容易造成氣泡聚并和破碎，導致氣泡的球形度減小。在床層底部區域，氣泡處于生成和生長期，氣泡球形度較大，幾乎近似于球形；而在床層的中上部，由于氣泡的聚并和破碎，引起氣泡拉長扭曲，最終導致氣泡的球形度減小。

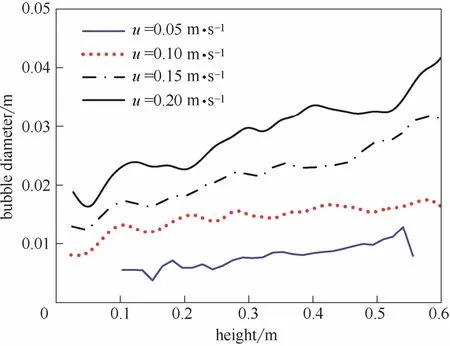
圖7　不同表觀氣速下氣泡平均當量直徑的軸向分布（5～25 s）Fig. 7　Axial profiles of time-averaged bubble equivalent diameter under different superficial gas velocity at 5—25 s

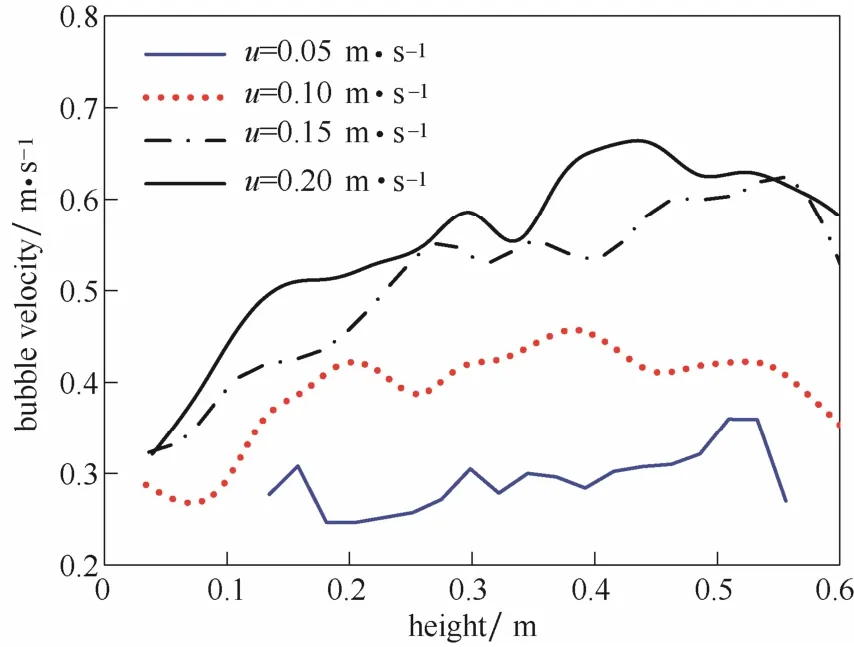
圖8　不同表觀氣速下氣泡平均速度的軸向分布（5～25 s）Fig. 8　Axial profiles of time-averaged bubble velocity under different superficial gas velocity at 5—25 s

圖9　不同表觀氣速下氣泡球形度的軸向分布（5～25 s）Fig. 9　Axial profiles of bubble sphere coefficient under different superficial gas velocity at 5—25 s

為了更加詳細地分析氣泡在鼓泡床內分布特性，統計了20～21 s時間內不同表觀氣速下床層內的所有氣泡分布情況，如圖10所示。由圖10可知，在較低氣速下，床層內的氣泡數目較少，氣泡較小，大部分氣泡趨于在床層中上部生成。隨著氣速的增大，床層內氣泡的數目不斷增加，氣泡的大小也在逐漸增加。總體來看，小氣泡多集中在床層底部區域，而大氣泡多集中在床層的中上部；從徑向分布來看，大氣泡多集中在床層中間區域，小氣泡多集中在床層壁面區域。且隨著表觀氣速的增加，氣泡的運動路徑呈彎曲上升趨勢，中心區域的氣泡在上升過程中，不斷發生著氣泡的增長和聚并，氣泡的大小不斷增大。在鼓泡床內，生命周期較長的氣泡對床層內顆粒的混合、傳熱、傳質和反應性能有著較大的影響。進一步統計了床層10～25 s內生命周期大于0.5 s的氣泡出現的次數，并統計出床層氣泡熱區分布，如圖11所示。由圖11可知，在較低的氣速下，床層內僅存在少量的長周期氣泡。隨著氣速的增大，長周期氣泡的數目不斷增加，且多集中在床層中部。

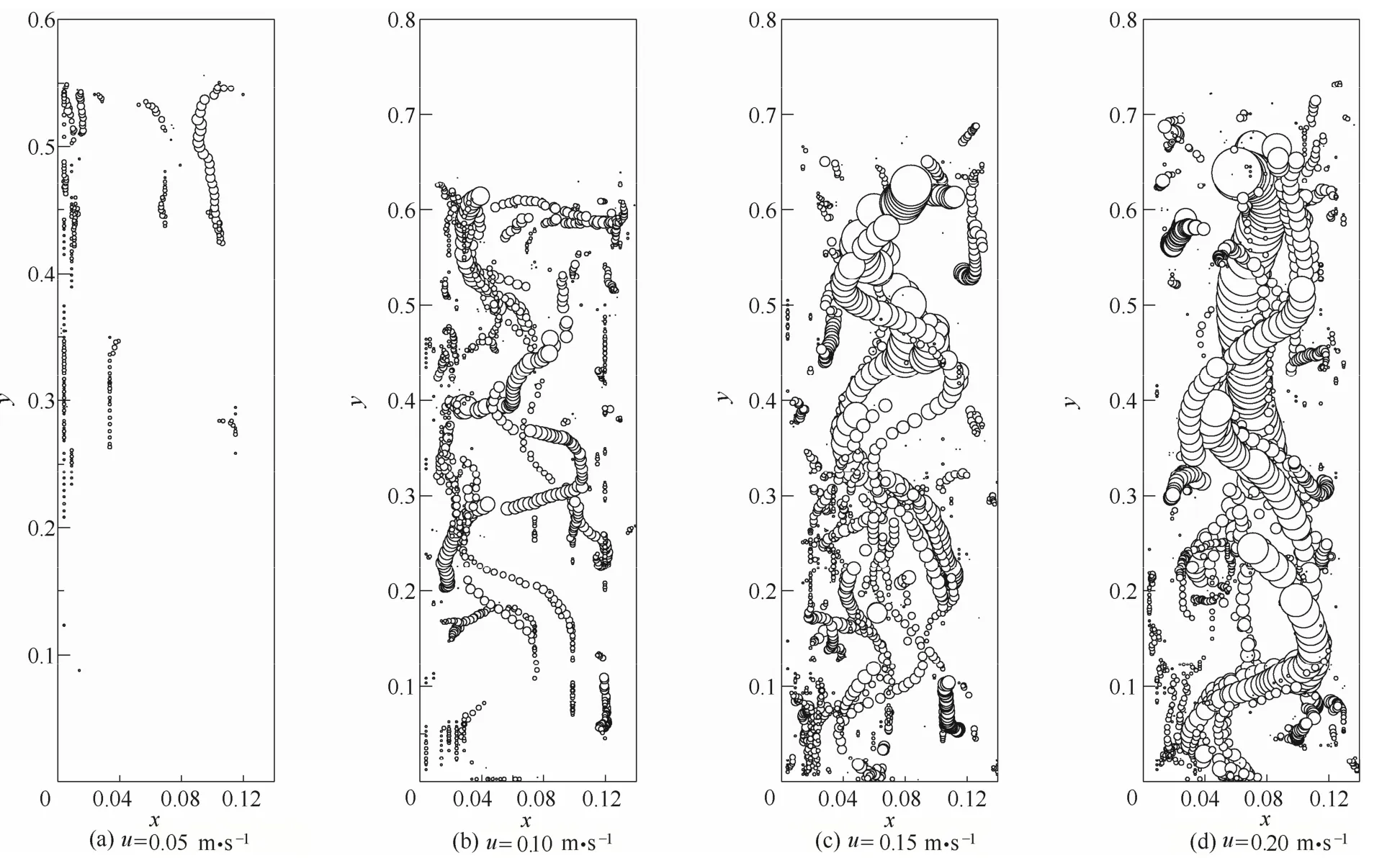
圖10　20～21 s內不同表觀氣速下床層內的氣泡分布Fig. 10　Distributions of bubble under different superficial gas velocity at 20—21 s

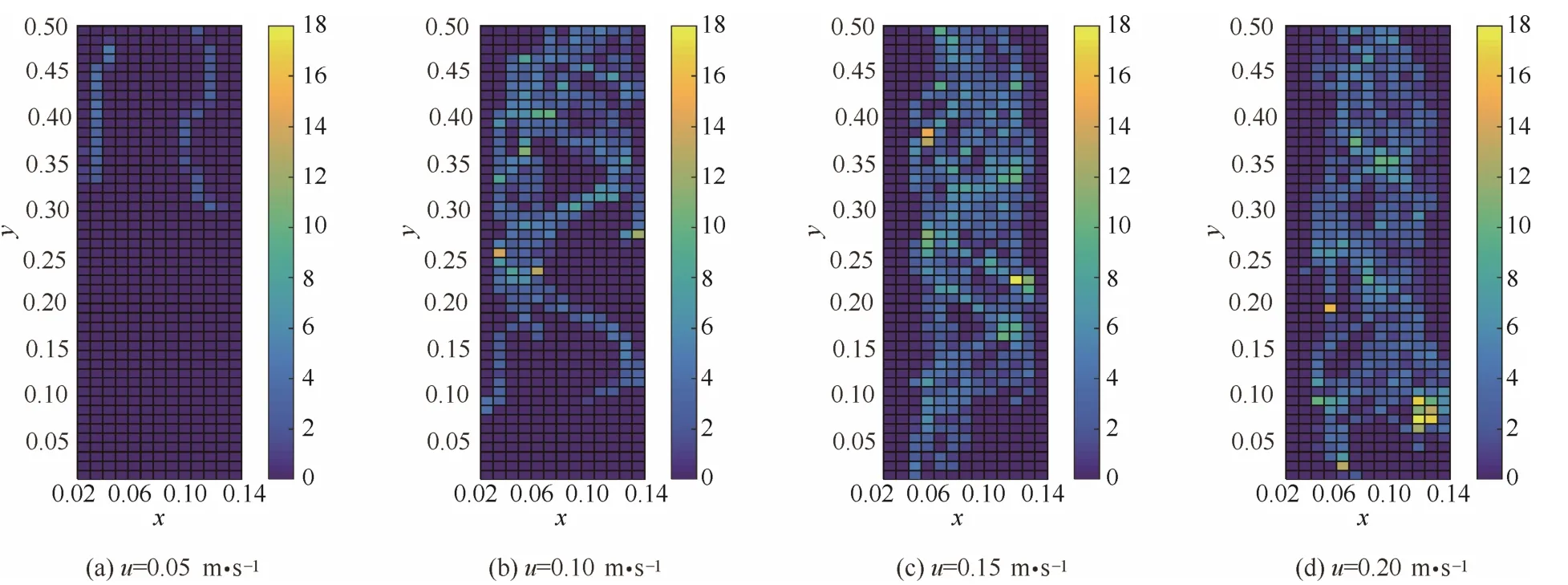
圖11　不同表觀氣速床層內氣泡生命周期大于0.5 s的氣泡熱區圖Fig. 11　Bubble hot spots at different superficial gas velocity for bubble life cycle of over 0.5 s

4　結　論

本文首先采用歐拉雙流體方法結合 EMMS曳力模型對氣固鼓泡床內的氣固流動特性進行模擬研究，并建立了識別和分析鼓泡床內氣泡特性的方法，分析了不同表觀氣速下氣泡沿床層軸向方向上的分布特性，包括氣泡平均當量直徑、氣泡速度以及氣泡球形度的軸向分布，進一步詳細地分析了不同氣速下氣泡在鼓泡床內的分布特性，得到了以下結論：隨著表觀氣速的增大，床層高度不斷增加，氣泡的球形度降低；在床層高度為0～50 cm內，床層內的固含率隨表觀氣速的增大不斷降低；同時沿床層高度方向，氣泡的大小也明顯變大。在鼓泡床底部，隨著表觀氣速的增大，氣泡產生的頻率顯著增加。在較低表觀氣速下（0.05 m·s-1），床層界面清晰；而在較高表觀氣速下（0.20 m·s-1），床層界面出現較大波動；在較高的表觀氣速下（0.15 m·s-1和0.20 m·s-1），由于氣固之間存在強烈的湍動作用，隨著床層高度的增加，氣泡上升速度增加。但當表觀氣速增大一定程度，繼續增加氣速對氣泡上升速度的影響不大；小氣泡多集中在床層底部和壁面區域，而大氣泡多集中在床層中間區域。且隨著表觀氣速的增大，氣泡的運動路徑呈彎曲上升趨勢，中心區域的氣泡不斷生長和聚并，導致氣泡不斷增大；在較低的表觀氣速下，床層內僅存在少量的長周期氣泡。隨著表觀氣速的增大，長周期氣泡的數目不斷增加，且多集中在床層中部。本文建立了識別和分析鼓泡床內氣泡特性的方法，仍缺乏對氣泡的聚并和破碎過程的追蹤，后期的工作仍需進一步完善。

符號說明

A ——氣泡直徑，m

C ——氣泡球形度

CD——曳力系數，kg·m-3·s-1

f ——修正因子

I ——單位張量

kΘs——顆粒脈動動能擴散系數

S ——氣泡周長，m

u ——速度/表觀氣速，m·s-1

V ——速度矢量，m·s-1

β ——曳力，kg·m2·s-1

γΘs——碰撞耗散能，kg·m-1·s-3

ε ——空隙率

Θs——顆粒溫度，m2·s-2

ρ——密度，kg·m-3

τ ——應力

下角標

g——氣相

p——顆粒

s——固相/顆粒相

References

［1］ 金涌， 祝京旭， 俞芷青. 流態化工程原理［M］. 北京: 清華大學出版社， 2001.

JIN Y， ZHU J X， YU Z Q. Fluidization Engineering Principles［M］. Beijing: Tsinghua University Press， 2001.

［2］ ZHU H P， ZHOU Z Y， YANG R Y， et al. Discrete particle simulation of particulate systems: a review of major applications and findings ［J］. Chem ical Engineering Science， 2008， 63（23）: 5728-5770.

［3］ ZOU L M， GUO Y C， CHAN C K. Cluster-based drag coefficient model for simulating gas-solid flow in a fast-fluidized bed［J］. Chem ical Engineering Science， 2008， 63（4）: 1052-1061.

［4］ MAKKAW I Y， WRIGHT P， OCONE R. The effect of friction and inter-particle cohesive forces on the hydrodynam ics of gas-solid flow: a comparative analysis of theoretical predictions and experiments［J］. Powder Technology， 2006， 163: 69-79.

［5］ GIDASPOW D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions［M］. Boston: American Press， 1994.

［6］ WEN C， YU Y. Mechanics of fluidization［J］. Chem ical Engineering Progress Symposium Series， 1966， 62: 100-111.

［7］ ERGUN S. Fluid flow through packed columns［J］. Chem ical Engineering Progress， 1952， 48: 89-94.

［8］ TURTON R， LEVENSPIEL O. A short note on the drag correlation for spheres［J］. Powder Technology， 1986， 47: 83-86.

［9］ MCKEEN T， PUGSLEY T. Simulation and experimental validation of a freely bubbling bed of FCC catalyst［J］. Powder Technology，2003， 129（1）: 139-152.

［10］ FERSCHNEIDER G， MEGE P. Eulerian simulation of dense phase fluidized beds［J］. Rev. Inst. Fr. Pe’t.， 1996， 51（2）: 301-307.

［11］ KRISHNA R， VAN BATEN J M. Using CFD for scaling up gas-solid bubbling fluidized bed reactors w ith Geldart A powders［J］. Chem ical Engineering Journal， 2001， 82（2）: 247-257.

［12］ BAYLE J， MEGE P， GAUTHIER T. Dispersion of bubble flow properties in a turbulent FCC fluidized bed［M］// Fluidization X，Engineering Foundation. New York， 2001: 125-132.

［13］ WANG W， LI J H. Simulation of gas-solid two-phase flow by a multi-scale CFD approach-extension of the EMMS model to the sub-grid level［J］. Chem ical Engineering Science， 2007， 62（1/2）: 208-231.

［14］ LI F. Investigations on the turbulent gas-solid two-phase interactions in fluidized desulfurization process［D］. Beijing: Tsinghua University，2009.

［15］ LU B. EMMS-based meso-scale model and its application in simulating gas-solid two-phase flows［D］. Beijing: Chinese Academy of Sciences， 2009.

［16］ ZHOU Q， WANG J， LI J. Three-dimensional simulation of dense suspension upflow regime in high-density CFB risers w ith EMMS-based two-fluid model［J］. Chem ical Engineering Science，2014， 107: 206-217.

［17］ JIRDILOK V， GIDSSPOW D， DAMRONGLERD S. et al. Kinetic theory based CFD simulation of turbulent fluidization of FCC particles in a riser［J］. Chemical Engineering Science， 2006， 61（17）: 5544-5559.

［18］ QI H， LI F， XI B， et al. Modeling of drag with the Eulerian approach and EMMS theory for heterogeneous dense gas-solid two-phase flow［J］. Chemical Engineering Science， 2007， 62（6）: 1670-1681.

［19］ NIKOLOPOULOS A， ATSONIOS K， NIKOLOPOULOS N， et al. An advanced EMMS scheme for the prediction of drag coefficient under a 1.2 MWth CFBC isothermal flow（Ⅱ）: Numerical implementation［J］. Chemical Engineering Science， 2010， 65（13）: 4089-4099.

［20］ BENYAHIA S， SUNDARESAN S. Do we need sub-grid scale corrections for both continuum and discrete gas-particles flow models［J］. Powder Technology， 2011， 220: 2-6.

［21］ LU B， WANG W， LI J. Eulerian simulation of gas-solid flows with particles of Geldart groups A， B and D using EMMS-based meso-scale model［J］. Chemical Engineering Science， 2011， 66（20）: 4624-4635.

［22］ SHI Z， WANG W， LI J. A bubble-based EMMS model for gas-solid bubbling fluidization［J］. Chemical Engineering Science， 2011， 66（22）: 5541-5555.

［23］ VERMA V， PADDING J T， DEEN N G. Effect of bed size on hydrodynamics in 3D gas-solid fluidized beds［J］. AIChE Journal，2015， 61（5）: 1492-1506.

［24］ EVGENIDIS S P， KARAPANTSIOS T D. Effect of bubble size on void fraction fluctuations in dispersed bubble flows［J］. International Journal of Multiphase Flow， 2015， 75: 163-173.

［25］ LU Y， HUANG J， ZHENG P. Flow structure and bubble dynamics in supercritical water fluidized bed and gas fluidized bed: a comparative study［J］. International Journal of Multiphase Flow， 2015， 73: 130-141.

［26］ ASEGEHEGN T W， SCHREIBER M， KRAUTZ H J. Investigation of bubble behavior in fluidized beds with and without immersed horizontal tubes using a digital image analysis technique［J］. Powder Technology， 2011， 210（3）: 248-260.

［27］ LV X， LI H， ZHU Q. Simulation of gas-solid flow in 2D/3D bubbling fluidized beds by combining the two-fluid model with structure-based drag model［J］. Chemical Engineering Journal， 2014， 236: 149-157.

［28］ CLOETE S， JOHANSEN S T， AMINI S. Investigation into the effect of simulating a 3D cylindrical fluidized bed reactor on a 2D plane［J］. Powder Technology， 2013， 239: 21-35.

［29］ GIDASPOW D， JUNG J， SINGH R K. Hydrodynamics of fluidization using kinetic theory: an emerging paradigm: 2002 Flour-Daniel lecture［J］. Powder Technology， 2004， 148: 123-141.

Numerical simulation of gas-solid bubbling bed and bubble characteristics based on EMMS drag model

WU Yingya， PENG Li， GAO Jinsen， LAN Xingying
（State Key Laboratory of Heavy Oil Processing， China University of Petroleum， Beijing 102249， China）

The gas-solid flow in gas-solid bubbling fluidized bed was simulated by a combined approach of computational fluid dynam ics （CFD） and the two fluid model （TFM）， based on the modified EMMS drag model. A new image processing method derived from image calibration was applied to study bubble characteristics w ith focus on overall and radial distributions of bubbles as well as bubble profiles in terms of averaged equivalent diameter， rising velocity， degree of sphericity， and bubble lifetime at various superficial gas velocity. The results showed that smaller bubbles most located at the bottom of beds and wall region whereas larger bubbles most located at the central region of beds. With increase of superficial gas velocity， the bed height were gradually increased and bubble profiles of the averaged equivalent diameter， the frequency of occurrence， the rising velocity and the lifetime were all increased except that the degree of sphericity was decreased. Nevertheless， once the superficial gas velocity increased to a certain level， its increase would no longer have any significant impact on the rising velocity.

gas-solid bubbling fluidized bed； multiphase flow； computational fluid dynam ics ； TFM； EMMS；bubble

date: 2016-04-07.

LAN Xingying， lanxy@cup.edu.cn

supported by the National Basic Research Program of China （2012CB215003） and the New Century Excellent Talents Program in University（NCET-13-1027）.

TQ 021.1

A

0438—1157（2016）08—3259—09

10.11949/j.issn.0438-1157.20160441

2016-04-07收到初稿，2016-06-08收到修改稿。

聯系人：藍興英。第一作者：吳迎亞（1990—），男，博士研究生。

國家重點基礎研究發展計劃項目（2012CB215003）；教育部新世紀優秀人才支持計劃項目（NCET-13-1027）。