"蘭利問題"求解的多種途徑

山東省臨沂市臨港經濟開發區第四中學　李艷娜

"蘭利問題"求解的多種途徑

一、問題再現

如圖1,△ABC中,AB=AC,∠A=20°,若E在AB上,D在AC上,∠CBD=50°,∠BCE=60°,求∠CED的度數.

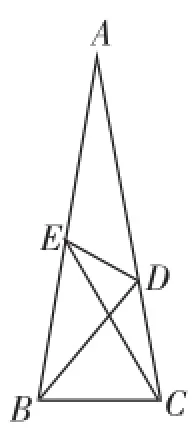
圖1

這個問題的歷史非常悠久,保守估計也有上百年的歷史,其最初的來源現在已經不得而知了.1922年,英國數學家蘭利在《數學公報》雜志上發表了一篇題為《一個問題》的文章,向人們詳細介紹了這個問題.這可能是該問題第一次正式出現在公眾的視野中,因此它也被稱為"蘭利問題".

第一次看到蘭利問題,相信同學們肯定會說"這還不容易",隨即拿起身邊的鉛筆,在草稿紙上涂畫起來.不過,大家馬上就會發現,僅僅去尋找角度上的數量關系,很快便會陷入僵局.即使將要求的角設為x,列出的方程也無法提供任何有用的信息.事實上,蘭利問題遠沒有那么簡單.解決這個問題不僅需要作出不止一條輔助線,而且還要構造出大量新的三角形!不過,雖然解題步驟異常煩瑣,但里面所用到的知識點都是大家已經學過的.難怪很多人都把這個問題稱為"史上最難的初等幾何問題".

雖然這是一道"史上最難的初等幾何問題",但用到的知識點都是大家已經學過的,所以我們應該相信經過思考和努力,能夠解答這個問題.

親愛的同學們,你敢向這道難題挑戰嗎?如果你經過思考和努力,仍然沒有破解這道難題,也不要懈氣.

二、解法探究

實際上,△ABC是一個比較特殊的等腰三角形,它的頂角為20°,兩個底角都為80°,注意到底角與頂角之差為60°,且BC=CD,若以∠ABC為底角,BC為一腰作等腰三角形BCF,并連接DF,這樣不僅可以得到一個等邊三角形CDF,還可以得到兩個等腰三角形CEF和DEF,再求∠CED就方便多了.

解法1:由AB=AC,∠A=20°,得∠ABC=∠ACB=80°.

由∠BDC=180°-∠CBD-∠ACB=180° -50°-80°=50°=∠CBD,得BC=CD.

作CF=BC交AB于點F,連接DF,則CF= CD,∠ABC=∠BFC=80°.

∠BCF=180°-2∠ABC=180°-2X80°=20°.

∠ACF=∠ACB-∠BCF=80°-20°=60°.

則△CDF是等邊三角形.則CF=DF,∠CFD=60°.

∠BFD=∠BFC+∠CFD=80°+60°=140°.

∠FCE=∠BCE-∠BCF=60°-20°=40°,∠FEC=180°-∠ABC-∠BCE=180°-80°-60°=40°=∠FCE,則EF=CF.又CF=DF,則EF=DF.

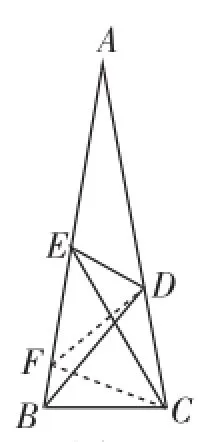
圖2

則∠CED=∠DEF-∠FEC=70°-40°=30°.

點評:輔助線CF在本解法中起著至關重要的作用,它溝通了△BFC、△DEF、△CEF和△CDF之間的聯系.正如一盤棋賽,看似死局的一方如果走動其中一枚關鍵的棋子,其他棋子都跟著動起來,全盤皆活.另外我們發現,點F是△CDE的外接圓(該圓半徑正好等于等腰三角形ABC的底邊長)的圓心,因此在得出EF=CF后,可以確定點F是△CDE的外接圓圓心,由同弧所對的圓周角與圓心角的關系立即可得∠CED=∠DFC=30°.

如果再能注意到BC=CD,聯想到正弦定理和余弦定理,若設BC=CD=1,則在△BCE中可以求出CE,而∠DCE=20°,利用余弦定理又可以求出DE之長,然后在△CDE中利用正弦定理求∠CED的度數.

解法2:設BC=CD=1.

在△CDE中,∠DCE=∠ACB-∠BCE=80°-60°=20°.

由余弦定理,得DE2=CD2+CE2-2CD.CE.cos∠DCE= 12+(2cos40°)2-2.2cos40°.cos20°=12+(2cos40°)2-2. 2cos40°cos20°=12+(2cos40°)2-2(cos60°+cos20°)=1+ 4cos240°-1-2cos20°=4cos240°-2cos20°=2(1+cos80°)-2cos20°=2+2cos80°-2cos20°=2+2(cos80°-cos20°)=2+ 2(-2sin50°sin30°)=2-2sin50°=2-2cos40°=2(1-cos40°)= 2.2sin220°=(2sin20°)2.

則DE=2sin20°.

點評:本解法利用正弦定理和余弦定理求解,思路清晰,目的性強,解答的關鍵是求出DE=2sin20°.

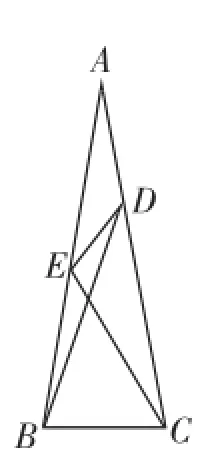
圖3

三、改變部分條件探究

如果將蘭利問題中的條件"∠CBD=50°"改為"∠CBD=70°",問題中的"求∠CED的度數"改為"求∠BDE的度數",又該如何求解呢?

如圖3,△ABC中,AB=AC,∠A= 20°,若E在AB上,D在AC上,∠CBD= 70°,∠BCE=60°,求∠BDE的度數.

已知條件僅將"∠CBD=50°"改為"∠CBD=70°",題目難度大大增加.不過我們可以借助蘭利問題及其求解思路助解.解法1:由AB=AC,∠A=20°,得∠ABC=∠ACB=80°.∠BDC=180°-∠ACB-∠CBD=180°-80°-70°=30°,∠ACE=∠ACB-∠BCE=80°-60°=20°.

在∠ABC內部作∠MBC=50°,BM交AC于點M.

∠DBM=∠CBD-∠MBC=70°-50°=20°.

∠BMC=180°-∠MBC-∠ACB=180°-50°-80°=50°=∠MBC.

則BC=CM,∠DBM=∠ACE.

作CN=BC交AB于點N,連接MN、EM,如圖4.

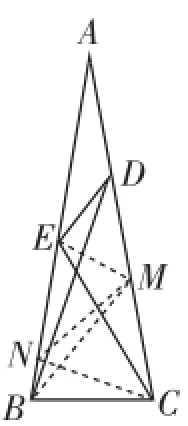
圖4

則CN=CM,∠ABC=∠BNC=80°,∠BCN=20°,∠ECN=∠BCE-∠BCN=60°-20°=40°,∠ACN=∠ACB-∠BCN=80°-20°=60°.

則△CMN是等邊三角形.則CN=MN,∠CMN=∠CNM=60°.

則∠BNM=∠BNC+∠CNM=80°+60°= 140°.

∠CEN=∠BNC-∠ECN=80°-40°=40° =∠ECN,則CN=EN.

則EN=MN.則∠EMN=70°.

∠EMD=180°-∠CMN-∠EMN=180°-60°-70°=50°=∠BMC.

則∠BMD=∠CME.又∠DBM=∠ACE,則△DBM∽△ECM.

則∠EDM=∠CBM=50°.則∠BDE=∠EDM-∠BDC= 50°-30°=20°.

點評:上述解法借助求解蘭利問題的圖形及其輔助線,通過兩次三角形相似求解,降低了解答難度.這也啟發我們學習數學要注意利用已有資源(數學結論、解題方法、思路等)幫助我們解決問題.

如果注意到BC是△BCD和△BCE的公共邊,利用正弦定理可以用含BC的式子表示出BD和BE之長,而∠ABD=10°,利用余弦定理可以求出DE之長,然后在△BDE中利用正弦定理求∠BDE的度數.

解法2:設BC=1.

在△BDE中,由余弦定理,得DE2=

即(sin40°DE)2=(sin60°)2+(2sin80°sin40°)2-2. sin60°.2sin80°.cos10°.sin40°

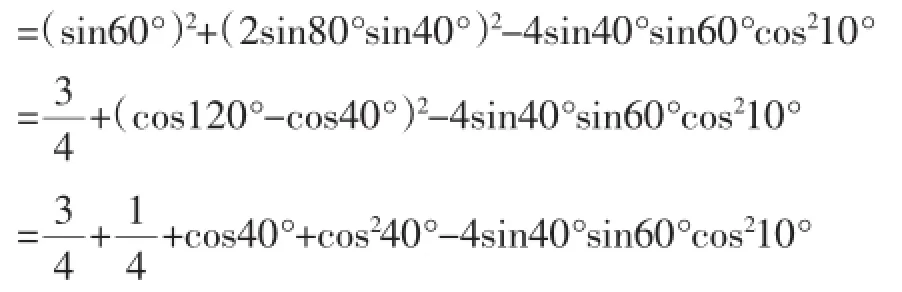
=1+cos40°+cos240°-4sin40°sin60°cos210°

=2cos220°+cos240°-2sin40°sin60°.2cos210°

=2cos220°+cos240°+(cos100°-cos20°)(1+cos20°)

=2cos220°+cos240°+cos100°-cos20°+cos100°cos20°-cos220°

=cos220°+cos240°+cos100°-cos20°+cos100°cos20°

=cos220°++cos80°)

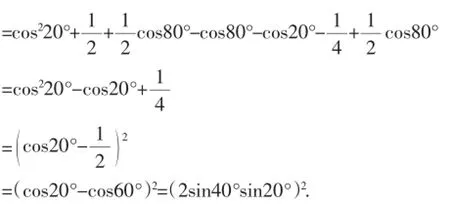
則sin40°DE=2sin40°sin20°.則DE=2sin20°.

則∠BDE=180°-∠ABD-∠BED=180°-10°-150°= 20°.

四、弱化條件探究

如果將蘭利問題中的條件"若E在AB上,D在AC上,∠CBD=50°,∠BCE=60°"改為"在AB上取一點D,使AD= BC",問題中的"求∠CED的度數"改為"求∠ACD的度數",又該如何求解呢?

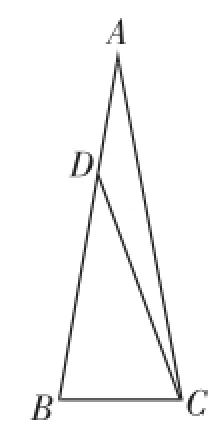
圖5

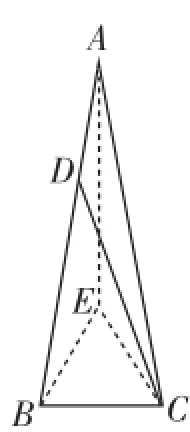
圖6

如圖5,△ABC中,AB=AC,∠A=20°,在AB上取一點D,使AD=BC,求∠ACD的度數.

為了利用條件"AD=BC",可以BC為邊構造等邊三角形,并連接AE,借助全等三角形求解.

解法1:如圖6,以BC為邊構造等邊三角形BCE,連接AE.

由AB=AC,∠A=20°,得∠ABC=∠ACB=80°.

易證△ADC≌△CEA,則∠ACD=∠EAC=10°.

當然,由AD=BC,可設AD=BC=1,然后在△ABC中,利用正弦定理求出AC,在△ACD中,利用余弦定理求出CD,在△ACD中,利用正弦定理求∠ACD的度數.

解法2:設AD=BC=1.

在△ACD中,由余弦定理,得CD2=AD2+AC2-2AD. AC.cosA

=12+(1+2cos20°)2-2(1+2cos20°)cos20°

=1+1+4cos20°+4cos220°-2cos20°-4cos220°

=2+2cos20°=2(1+cos20°)

=2.2cos210°=(2cos10°)2,則CD=2cos10°.

則sin∠ACD=sin10°.則∠ACD=10°.

可以看出,蘭利問題及根據蘭利問題改編的問題(一般都是競賽題),都可以利用初中方法和高中方法求解,利用初中方法求解需要作的輔助線一般不少于兩條,而且輔助線的作法非常巧妙,不容易想到.而利用高中三角知識求解思路清晰、解題目標明確,但在利用余弦定理求某一線段長時難度較大,不僅運算量大,而且需要對三角知識掌握得比較嫻熟.可見利用初中方法和高中方法解決蘭利問題及根據蘭利問題改編的問題各有千秋!