精確醫學與大數據

郭毅可，楊　氙（1.上海大學計算機工程與科學學院，上海00444；.倫敦帝國理工學院數據科學研究所，倫敦SW7 AZ）

精確醫學與大數據

郭毅可1，2，楊氙2
（1.上海大學計算機工程與科學學院，上海200444；2.倫敦帝國理工學院數據科學研究所，倫敦SW7 2AZ）

為了實現精確醫學，需要采集和分析大量數據來量化每個病人.首先討論了從分子層面到鏈路層面的數據，同時闡述了使用醫療圖像數據的必要性.不同數據類型雖然需要有不同的預處理方式，但是在預處理完成后，通常可以使用通用的方法對這些數據進行分析，如分類和網絡分析.從研究問題的角度討論了多種分別用于解答不同復雜度問題的研究方法.這些由簡單到復雜的問題包括關聯性檢測、歸類分析、構建分類器、獲得網絡連接和動態模型構建.

精確醫學；大數據；分析方法

未來人們到醫院看病時，可能會看到基于自己獨特分子信息和生理狀態的計算機仿真個體.使用仿真個體，醫生可以為每個病人設計最適合的治療方案.精確醫療這門學科致力于研究每位患者的疾病易感性、生物學基礎和對藥物的反應，從而定制治療措施.這是醫療研究領域的一個重大轉變，意味著疾病的診斷和治療將基于對病人各種分子層面的大數據、臨床數據、生理學數據的研究和挖掘.對各種類型的大數據進行挖掘需要提出相應的分析方法.例如，為了找到DNA中哪些位點的突變與疾病有關，需要進行全基因組關聯分析.在對不同數據類型提出相應分析方法的同時，還需要研究如何對不同數據中提取的信息進行整合.圖1展示了一種用不同分子數據對疾病進行預測的流程［1］.圖1（a）列出了分子（由L表示）及其對應的測量值（由X表示）；圖1（b）分析了這些分子的相關作用，圖中的點表示分子，邊表示分子的關聯；圖1（c）進一步學習了這些分子濃度的交叉分布（非獨立分布），如多元正態分布，從而為疾病診斷提供可行性.

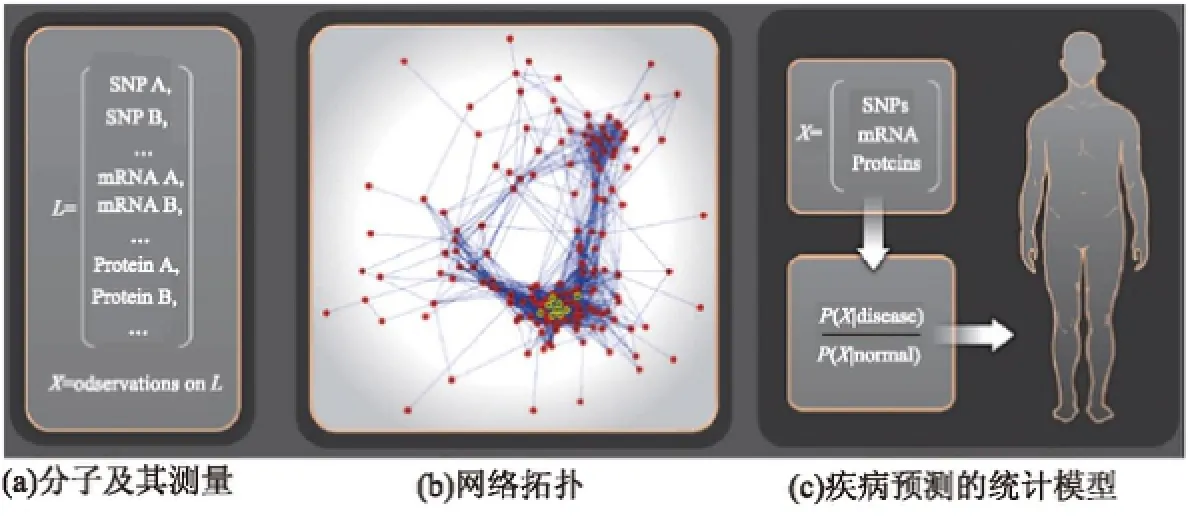
圖1　用不同分子數據對疾病進行預測的示例Fig.1　Examples of disease prediction with different molecular data

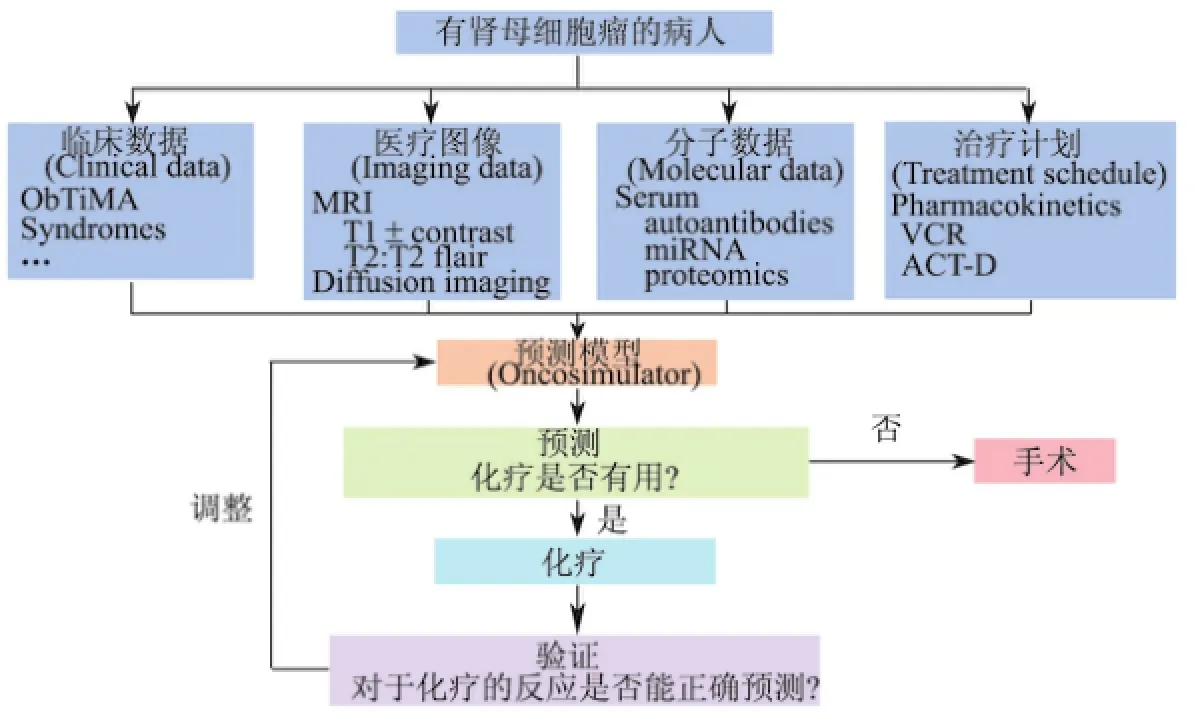
圖2　用預測模型對癌癥病人是否應接受術前化療的預測流程圖Fig.2　Flowchart of prediction model of whether cancer patient should accept preoperative chemotherapy or not

下面用一個在醫療診斷中的實例來說明綜合應用不同類型大數據的必要性.圖2呈現了如何預測術前化療能否對腎母細胞瘤（nephroblastoma）進行有效抑制［2］.在這個預測流程中用到了臨床數據、醫療圖像、分子數據等來構建預測模型（oncosimulator）.在臨床實驗中，新病人會被隨機分入兩組：A組的病人將接受現有的術前化療；B組的病人將根據預測模型接受治療.在B組，如果模型預測腫瘤因化療而萎縮，則醫生會對病人進行術前化療；反之，病人將會直接進行手術而不必忍受術前化療的風險和痛苦.對比這兩個不同實驗組的結果，可以顯示出基于大數據建立預測模型的益處［2］.然而，要完成這樣一個預測流程需要應用大量的數學分析方法.

1　大數據在精確醫學中的應用

1.1分子數據的應用

為了實現精確醫學，需要綜合應用各種各樣的分子數據.典型的數據類型包括基因序列、基因表達（可由Microarray或者RNA-seq技術來測量）和蛋白質表達（可由質譜儀來測量）.不同的數據可描述生物系統的不同方面，通過對這些大數據進行分析，可以找到特定病理狀態的生物標記或建立基本診斷模型.

下面以Ubiopred1UbiopredstandsforUnbiasedBIOmarkersinPREDictionofrespiratorydiseaseoutcomes. http://www.europeanlung.org/en/projects-and-research/projects/u-biopred/home項目為例來展現分子數據在精確醫學中的應用.Ubiopred項目采集上千個重癥哮喘病人的樣本和臨床數據，用以找到重癥哮喘的亞型.疾病亞型的識別會大大增加治療的準確性，這也是精確醫學的一個重要研究課題.Ubiopred項目生成了多種組學數據（omics），包括基因組學、測序和轉錄組學、蛋白組學、脂肪和代謝組學.與此同時，其他一些類型的數據如組織學、形態學、臨床和病歷也都一一采集.基于這些數據可以得到一個完善的重癥哮喘分型模型.

圖3展現了Ubiopred項目的研究流程：步驟一，首先采集大量的成人和兒童重癥哮喘病人樣本，這些樣本可用于進行橫向和縱向研究；步驟二，使用各種類型的大數據，運用系統生物學方法生成一個生物標記的掌印（handprint）來對病人進行亞型分類；步驟三，生物標記掌印的準確性將由疾病的進展和惡化程度來驗證；步驟四，用動物模型和體外人體模型來修正生物標記的掌印.步驟二是項目的核心部分，該步驟在很大程度上依賴于對各種大數據的分析和挖掘.可以說，如果沒有這些大數據，則很難對重癥哮喘進行準確而又全面的分型.

1.2從分子層面到鏈路層面的研究

在Ubiopred項目中生成的生物標記掌印包括一些基因、蛋白質、脂肪和其他分子.可以將這些生物標記掌印映射到生物鏈路上以了解哪些鏈路對疾病分型起作用.通過對這些生物鏈路的分析可以進一步理解不同亞型的病理.計算機仿真模型可以模擬不同亞型背后的生物過程，在建模過程中需要使用采集自縱向研究的時序數據.圖4解釋了從分子層面到生物鏈路層面的整個研究過程.在更高層面進行研究對于精確醫學有著重要的意義，這是因為通過分子的相互作用才能完成復雜的生物過程.因此需要同時全面地研究各種不同種類分子的行為和表達，而最為直接的方法就是將它們映射到鏈路上.

1.3醫學圖像的應用

除了分子數據外，醫學圖像數據同樣也可以用于精確醫學中對疾病進行診斷.最常見的醫學圖像包括核磁共振（magnetic resonance imaging，MRI）、電子計算機斷層掃描（computed tomography，CT）、正電子發射斷層顯像（positron emission computed tomography，PET）和超聲波.這些醫學圖像數據可以提供病人的一些重要特征，如解剖結構、組織形態及分布.從這些圖像數據中提取出對醫生有用的信息用于診斷需要使用多種分析方法.隨著越來越多創新技術和方法的提出，可以期待在不久的將來，醫療圖像數據將廣泛應用于疾病診斷模型中.

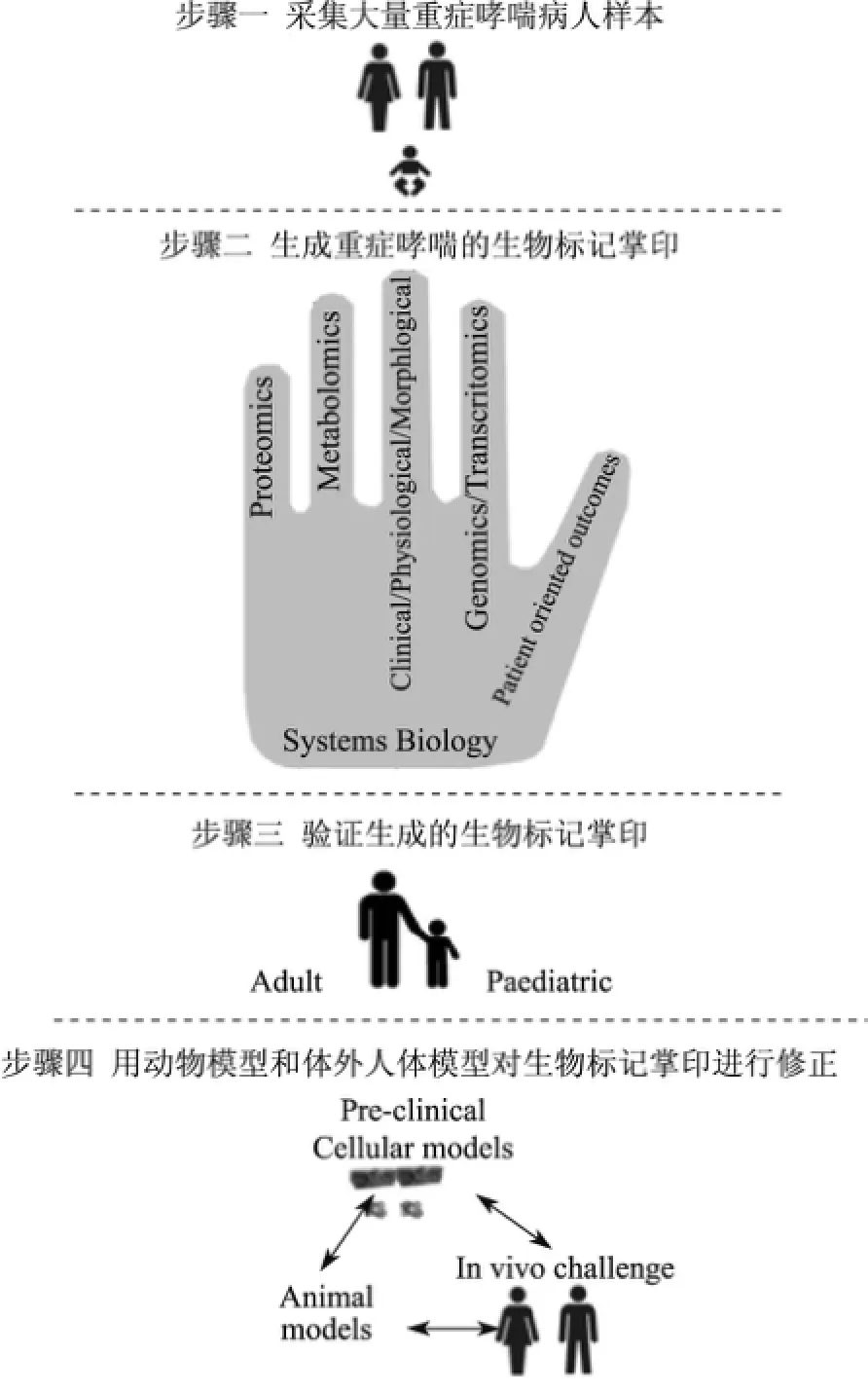
圖3　Ubiopred項目的研究流程Fig.3　Research process of Ubiopred project

2　主要研究問題和分析方法的綜述

在精確醫學研究中需要回答各種問題，而每種問題都需要有相應的分析方法.圖5列舉了精確醫學研究中會遇到的一些典型研究問題及其示例.這些研究問題從簡單到復雜，需要采用不同的分析方法.例如，一個最典型的問題就是找到哪些分子（如基因、蛋白質、脂肪）在用藥前后的表達產生了顯著變化，這時只需要進行相對簡單的顯著性檢測就可得到答案.如果想進一步找到哪些分子的變化是相關的，就需要再進行相關性檢測.然而，在很多研究中僅僅進行顯著性和相關性檢測還不夠，常常需要進行更多的研究來深入了解復雜的數據.所以，往往會用到一些更復雜的分析方法，如機器學習.例如，聚類算法可用來尋找潛在的數據組群，分類算法可用來進行數據擬合.如果想進一步了解復雜系統的機理，則需要使用網絡構建方法（如構建蛋白質相互作用網絡和基因調控網絡）來獲得分子間的相互關系.為了解釋系統的動態變化，還需要運用數學建模的方法來獲得動力學模型.這些都需要采集大量的縱向數據，并且使用不同的分析方法來尋找合適的參數以擬合時間數據.下面簡單介紹一下用于五種典型問題的分析方法.

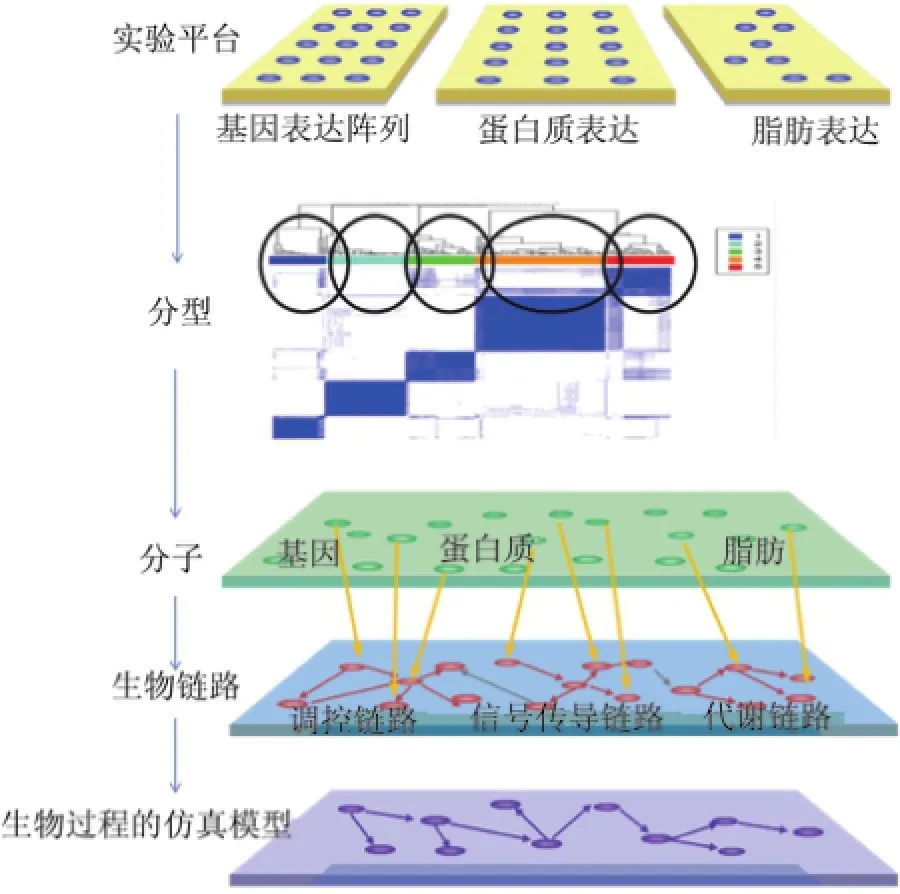
圖4　從分子層面到生物鏈路層面的研究過程Fig.4　Research procedure from molecular level to biological pathway level

2.1關聯性檢測（detecting associations）

一個典型的研究問題就是找到哪些變量與反應量有關.例如，全基因組關聯分析（genomewide association study，GWAS）就是要尋找哪些基因突變與表型有關.又比如在基于事件觸發的fMRI分析中，要找到哪些腦區域與外部刺激相關聯.這里用X=［x1，x2，···，xN］表示變量，用Y表示反應量.如果不考慮其他變量的影響，只獨立判斷第n個變量xn與Y的關系，那么可以采取多種成對比較方法，如皮爾遜相關系數（Pearson correlation coefficient）法［4］、斯皮爾曼等級相關系數（Spearman's correlation coefficient）法［5］，以及基于互信息（mutual information）法演變出的最大信息系數（maximal information coefficient）法［6］.

如果考慮變量之間的相互影響，那么就需要同時檢測所有的變量X與Y的關系.可以構建如下線性模型［7］：

式中，Y為一個P×1的向量；β為一個N×1的向量，包含了需要預測的相關性；∈～N（0，σ2I）為一個噪聲向量，其中σ2是噪聲的方差.當P＞N時，估算β的一個典型方法就是最小二乘（least square）法.最小二乘法基于最小化殘差平方和（residual sum of squares），可以得到β的一個無偏估計值，即β=（X′X）-1X′Y.當P＜N時，可以采用另一種方法——Lasso（least absolute shrinkage^and selection operator）.該方法可以看成是在最小二乘法上加了一個限制條件［8-9］：

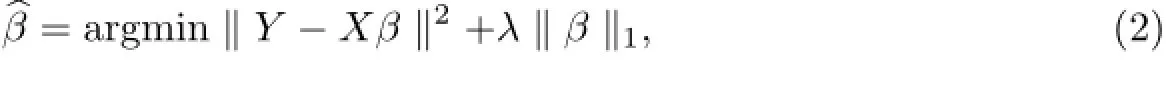
式中，λ為調控參數，‖·‖1表示l1-norm.可以采用多種優化方法求解式（2），如二次規劃法和凸優化法［10-15］.除了Lasso方法外，還可以采用最小角回歸法（least angle regression）［16］和稀疏貝葉斯學習（sparse Bayesian learning）［17］.需要指出的是，Lasso方法通過l1-norm對β的解的稀疏性進行控制，在稀疏貝葉斯學習中β的稀疏性則是由給定的稀疏先驗分布來實現的.

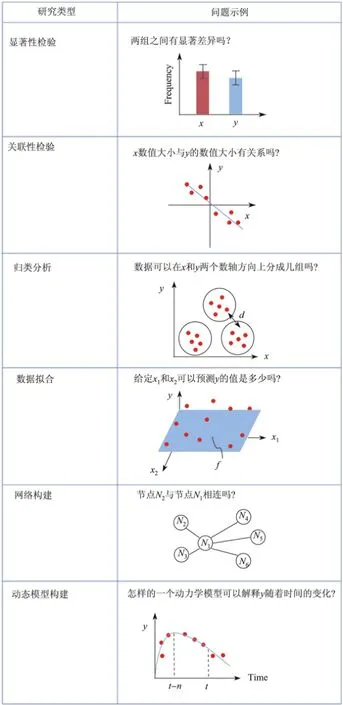
圖5　在精確醫學研究中的典型研究類型及相應問題示例Fig.5　Typical research types and related questions in precision medicine research

2.2歸類分析（identifying groups）

歸類分析是為了找到數據潛在的構造而將相似樣本歸為一組的一類分析方法.歸類分析在精確醫學中有著極其重要的作用.例如，在尋找哮喘病和乳腺癌的亞型研究［18-19］中，就運用了多種歸類方法作用在多種分子數據上（例如DNA甲基化（methylation）和mRNA表達數據）.概括地說，歸類算法可以分為兩類：最典型的一類就是聚類算法，如層次聚類（hierarchical clustering）法［20］、k-means聚類法［21］和混合模型（mixture models）法［22］；另一類是基于信號處理的方法，這類方法將數據分成獨立的成分，如主成分分析（principle component analysis）方法.

2.3構建分類器（constructing classifiers）

通常使用機器學習的方法來構建分類器.分類器可用來預測病人是否患病或患了哪種亞型的病.構建分類器的算法有很多種，包括線性分類算法（如線性判別分析（Fisher's linear discriminant）［23］、邏輯回歸（logistic regression）［24］、樸素貝葉斯（naive Bayesian）［25］、支持向量機（support vector machine，SVM）［26］、決策樹（decision trees）［27］、神經網絡（neural networks）［28］和相關向量機（relevance vector machine）［29］.很難說哪種算法一定優于其他算法，因為對于不同的數據需要通過比較各種算法的性能來選擇最適合的算法.而算法的性能可以通過以下方法來評估：赤池信息量準則（Akaike information criterion）［30］、貝葉斯信息準則（Bayesian information criterion）［31］、貝葉斯因子［32］和交叉驗證（cross-validation）［33］，其中交叉驗證法的使用非常廣泛，其基本思想是將原始數據分為訓練集和驗證集，然后用訓練集來構建分類器，并用驗證集來驗證.

在選定分類算法的同時，使用哪些特征（feature）來構建分類器也是一個重要的問題.這需要保證選定的特征具有穩定性，也就是在數據受到一定微小擾動的情況下，這些特征還是會被一致地選出.文獻［34-37］討論了特征穩定性的問題.文獻［38］提出的方法在取得特征穩定性的同時，還保證了分類器的預測準確性，該方法在尋找疾病的生物標記中得到應用.

2.4獲得網絡連接（deriving connectivity）

網絡的定義［39］是由點和點的兩兩連接組成的邊的集合，這里認為網絡連接（connectivity）是邊的集合.獲得網絡連接在精確醫學中有著重要意義，比如可以通過網絡連接獲知分子的相互關系.如果不考慮邊的方向性，可以直接使用兩兩相關性檢測和互信息的方法來推斷邊的存在.需要指出的是，這些方法會推斷出一些非直接關聯的邊（indirect link），這是由關聯的傳遞性造成的［40］.所以，一些研究致力于抑制非直接關聯的邊的生成，包括偏相關系數（partial correlation）法［41-43］、ICOV［44-45］和網絡去卷積（network deconvolution）法［40，46］.在推斷邊的存在性的同時，如果還需要推斷邊的方向性，可以使用以下方法：基于圖模型來判斷信息流的方法［47-48］、LiNGAM（linear，non-Gaussian，acyclic causal models）法［49］及其變形［50］、基于向量自回歸模型的格蘭杰因果關系（Granger causality）法［51］、Patel's條件依賴法［52］及廣義同步（generalised synchronisation）法［53］.文獻［54］比較了上述算法的性能，發現性能最優的3個算法是偏相關系數法、ICOV和貝葉斯網絡法.

2.5動態模型構建（building dynamic model）

動態模型可以使人們更好地了解生物過程的機理.從時序數據中推測動態模型是一項具有挑戰性的工作.目前已有多種推測方法，文獻［55］從8個角度來討論了這些推測方法，即反問題（inverse problems）、優化問題（optimisation）、系統與控制理論（systems and control theory）、化學反應網絡理論（chemical reaction network theory）、貝葉斯統計（Bayesian statistics）、物理學方法（physics）、信息理論（information theory）和機器學習（machine learning）.下面將從其中3個主要方向進行討論.

從優化角度來看，模型推測可以看作以目標函數為預測值和真實值差別的優化問題.如果該優化問題是凸的，可以采用凸優化方法［56］來尋找目標函數的最小點；如果該優化問題不是凸的，則很容易得到一個局域最小點而非全局最小點.已有一些算法嘗試解決這種非凸問題，如全局優化［57］.但是全局優化面臨的問題就是算法復雜度會隨著問題維度急速上升.

從系統與控制理論的角度來看，模型推測可以看作將估計參數轉變為狀態變量的過程［58-59］.一個典型的算法就是卡爾曼濾波器（Kalman filter）［60］.卡爾曼濾波器作為一個遞歸預測器，利用當前得到的新信息調整上一步得到的預測值.擴展卡爾曼濾波器（extended Kalman filter）和無損卡爾曼濾波器（unscented Kalman filter）已被用于構建信號傳導網絡［61-62］.但是該方法的一個缺點就是對算法中初始值的設定非常敏感.

從貝葉斯統計角度來看，模型推測可以看作運用貝葉斯定理通過最大似然（likelihood）來推測參數的概率分布.對于復雜的概率模型，計算似然非常困難，所以通常需要運用近似貝葉斯計算（approximate Bayesian computation）［63］.近似貝葉斯計算包括蒙特卡羅抽樣（Monte Carlo rejection sampling）、馬爾科夫鏈蒙特卡羅（Markov chain Monte Carlo）［64］、序貫蒙特卡羅（sequential Monte Carlo）［65］.另外，還可以考慮采用變分貝葉斯（variational Bayes）方法和Type-Ⅱ的方法［66］.

3　結束語

本研究討論了大數據在精確醫學中的作用，重點提到的數據類型包括分子層面數據、鏈路數據和醫學圖像數據.通過對大數據進行分析來回答不同的研究問題需要相應地使用不同的分析方法.重點討論了以下5種研究問題，由簡單到復雜依次為關聯性檢測、歸類分析、構建分類器、獲得網絡連接、動態模型構建.對于每種研究問題都列舉了一些典型的分析方法，這些分析方法可以交叉使用在不同領域和不同數據類型上.通過對大數據的分析，相信在不久的將來就可以實現精確醫學，以此對每個病人提供最適合的醫療方案.

［1］WINSLOW R L，TRAYANOVA N，GEMAN D，et al.Computational medicine：translating models to clinical care［J］.Sci Transl Med，2012，4（158）：158rv11.

［2］COVENEY P，D′IAZ-ZUCCARINI V，HUNTER P，et al.Computational biomedicine［C］// Computational Biomedicine.2014：296.

［3］WOLKENHAUER O.Why model？［J］.Front Physiol，2014，5：1-5.

［4］PEARSON K.Note on regression and inheritance in the case of two parents［J］.Proc R Soc London，2006，58（1）：240-242.

［5］PENG H，LONG F，DING C.Feature selection based on mutual information：criteria of maxdependency［C］//IEEE Trans Pattern Anal.2005：1226-1238.

［6］RESHEF D N，RESHEF Y A，FINUCANE H K，et al.Detecting novel associations in large data sets［J］.Science，2011，334（6062）：1518-1524.

［7］FREEDMAN D.Statistical models：theory and practice［M］.Cambridge：Cambridge University Press，2005.

［8］TIBSHIRANI R.Regression selection and shrinkage via the Lasso［J］.Journal of the Royal Statistical Society B，1994，58：267-288.

［9］CHEN S S，DONOHO D L，SAUNDERS M A.Atomic decomposition by basis pursuit［J］.SIAM Journal on Scientific Computing，1998，20（1）：33-61.

［10］BECKER S R，CAND`ES E J，GRANT M C.Templates for convex cone problems with applications to sparse signal recovery［J］.Math Program Comput，2011，3（3）：165-218.

［11］BOYD S.Distributed optimization and statistical learning via the alternating direction method of multipliers［J］.Found Trends Mach Learn，2010，3（1）：1-122.

［12］BECKER S，BOBIN J，CAND`ES E J.NESTA：a fast and accurate first-order method for sparse recovery［J］.SIAM J Imaging Sci，2011，4（1）：1-39.

［13］BECK A，TEBOULLE M.A fast iterative shrinkage-thresholding algorithm for linear inverse problems［J］.SIAM J Imaging Sci，2009，2（1）：183-202.

［14］FRIEDMAN J，HASTIE T，H¨OFLING H，et al.Pathwise coordinate optimization［J］.Annals of Applied Statistics，2007，1（2）：302-332.

［15］KING R，MORGAN B J T，GIMENEZ O，et al.Bayesian analysis for population ecology［M］.Boca Raton：CRC Press，2010.

［16］EFRON B，HASTIE T，JOHNSTONE I，et al.Least angle regression［J］.Ann Stat，2004，32（2）：407-499.

［17］TIPPING M E.Bayesian inference：an introduction to principles and practice in machine learning［J］.Lecture Notes in Computer Science，2004，3176：41-62.

［18］WU W，BLEECKER E，MOORE W，et al.Unsupervised phenotyping of Severe Asthma Research Program participants using expanded lung data［J］.J Allergy Clin Immunol，2014，133（5）：1280-1288.

［19］MOORE W C，MEYERS D A，WENZEL S E，et al.Identification of asthma phenotypes using cluster analysis in the Severe Asthma Research Program［J］.Am J Respir Crit Care Med，2010，181（4）：315-323.

［20］HASTIE T，TIBSHIRANI R F.The elements of statistical learning［M］.New York：Springer，2009.

［21］HARTIGAN J A，WONG M A.Algorithm AS 136：a k-means clustering algorithm［J］.Appl Stat，1979，28（1）：100.

［22］JENSEN D R.Mixture models：theory，geometry and applications［J］.Journal of Statistical Planning and Inference，1997，59（1）：179-181.

［23］FISHER R.The use of multiple measurements in taxonomic problems［J］.Ann Eugen，1936，7（2）：179-188.

［24］COx D R.The regression analysis of binary sequences（with discussion）［J］.J Roy Stat Soc B，1958，20：215-242.

［25］RISH I.An empirical study of the naive Bayes classifier［C］//IJCAI 2001 Workshop on Empirical Methods in Artificial Intelligence.2001：1-6.

［26］CORTES C，VAPNIK V.Support-vector networks［J］.Mach Learn，1995，20（3）：273-297.

［27］QUINLAN J R.Simplifying decision trees［J］.International Journal of Man-Machine Studies，1987，27（3）：221-234.

［28］BISHOP C M.Neural networks for pattern recognition［J］.J Am Stat Assoc，1995，92：482.

［29］TIPPING M E.Sparse Bayesian learning and the relevance vector machine［J］.Journal Mach Learn Res，2001，1（3）：211-244.

［30］AHO K，DERRYBERRY D，PETERSON T.Model selection for ecologists：the worldviews of AIC and BIC［J］.Ecology，2014，95（3）：631-636.

［31］SCHWARZ G.Estimating the dimension of a model［J］.The Annals of Statistics，1978，6（2）：461-464.

［32］TONI T，STUMPF M P H.Simulation-based model selection for dynamical systems in systems and population biology［J］.Bioinformatics，2010，26（1）：104-110.

［33］YANG X，GUO Y，SKIPP P，et al.Automating mass spectrometry proteomics analysis［C］//Fourth International Conference on Bioinformatics and Computational Biology.2012.

［34］ABEEL T，HELLEPUTTE T，VAN DE PEER Y，et al.Robust biomarker identification for cancer diagnosis with ensemble feature selection methods［J］.Bioinformatics，2009，26（3）：392-398.

［35］ZUCKNICK M，RICHARDSON S，STRONACH E A.Comparing the characteristics of gene expression profiles derived by univariate and multivariate classification methods［J］.Stat Appl Genet Mol Biol，2008，7（1）：Article7.

［36］AHMED I，HARTIKAINEN A L，J¨ARVELIN M R，et al.False discovery rate estimation for stability selection：application to genome-wide association studies［J］.Stat Appl Genet Mol Biol，2011，10（1）：1-20.

［37］ALExANDER D H，LANGE K.Stability selection for genome-wide association［J］.Genet Epidemiol，2011，35（7）：722-728.

［38］KIRK P，WITKOVER A，BANGHAM C R M，et al.Balancing the robustness and predictive performance of biomarkers［J］.J Comput Biol，2013，20（12）：979-989.

［39］NEWMAN M E J.Networks：an introduction［M］.Oxford：Oxford University Press，2010.

［40］BARZELB，BARAB′ASIAL.Networklinkpredictionbyglobalsilencingofindirect correlations［J］.Nat Biotechnol，2013，31（8）：720-725.

［41］DE LA FUENTE A，BING N，HOESCHELE I，et al.Discovery of meaningful associations in genomic data using partial correlation coefficients［J］.Bioinformatics，2004，20（18）：3565-3574.

［42］HEMELRIjK C K.A matrix partial correlation test used in investigations of reciprocity and other social interaction patterns at group level［J］.Journal of Theoretical Biology，1990，143（3）：405-420.

［43］VEIGA D F T，VICENTE F F R，GRIVET M，et al.Genome-wide partial correlation analysis of Escherichia coli microarray data［J］.Genet Mol Res，2007，6（4）：730-742.

［44］FRIEDMAN J，HASTIE T，TIBSHIRANI R.Sparse inverse covariance estimation with the graphical lasso［J］.Biostatistics，2008，9（3）：432-441.

［45］VAROqUAUx G，GRAMFORT A，POLINE J B，et al.Brain covariance selection：better individual functional connectivity models using population prior［C］//Advances in Neural Information Processing Systems.2010：2334-2342.

［46］FEIZI S，MARBACH D，M′EDARD M，et al.Network deconvolution as a general method to distinguish direct dependencies in networks［J］.Nat Biotechnol，2013，31（8）：726-733.

［47］WEIGT M，WHITE R A，SZURMANT H，et al.Identification of direct residue contacts in proteinprotein interaction by message passing［J］.Proc Natl Acad Sci，2009，106（1）：67-72.

［48］JORDAN M I，WAINWRIGHT M J.Graphical models，exponential families，and variational inference［M］//Foundations and Trends in Machine Learning.Boston：Now Publishers Inc，2008：1-305.

［49］SHIMIZU S.A linear non-Gaussian acyclic model for causal discovery［J］.J Mach Learn Res，2006，7：2003-2030.

［50］HYVARINEN A，SMITH S M.Pairwise likelihood ratios for estimation of non-Gaussian structural equation models［J］.J Mach Learn Res，2013，14：111-152.

［51］GRANGER C W J.Investigating causal relations by econometric models and cross-spectral methods［J］.Econometrica，1969，37（3）：424-438.

［52］PATEL R S，BOWMAN F D，RILLING J K.A Bayesian approach to determining connectivity of the human brain［J］.Hum Brain Mapp，2006，27：267-276.

［53］DAUWELS J，VIALATTE F，MUSHA T，et al.A comparative study of synchrony measures for the early diagnosis of Alzheimer's disease based on EEG［J］.Neuroimage，2010，49（1）：668-693.

［54］SMITH S M，MILLER K L，SALIMI-KHORSHIDI G，et al.Network modelling methods for FMRI ［J］.Neuroimage，2011，54（2）：875-891.

［55］VILLAVERDE A F，BANGA J R.Reverse engineering and identification in systems biology：strategies，perspectives and challenges［J］.J R Soc Interface，2014，11（91）：20130505.

［56］BOYD S，VANDENBERGHE L.Convex optimization［M］.Cambridge：Cambridge University Press，2004.

［57］GOUNARIS C，FLOUDAS C.A review of recent advances in global optimization［J］.J Glob Optim，2009，45（1）：3-38.

［58］SUN X，JIN L，XIONG M.Extended Kalman filter for estimation of parameters in nonlinear state-space models of biochemical networks［J］.PLoS One，2008，3（11）：e3758.

［59］FEY D，FINDEISEN R，BULLINGER E.Parameter estimation in kinetic reaction models using nonlinear observers facilitated by model exten［J］.Ifac World Congress Seoul Korea，2008，17（1）：313-318.

［60］WELCH G，BISHOP G.An introduction to the Kalman filter［J］.In Pract，2006，7（1）：1-16.

［61］LILLACCI G，KHAMMASH M.Parameter estimation and model selection in computational biology［J］.Plos Computational Biology，2010，6（3）：e1000696.

［62］QUACH M，BRUNEL N，D'ALCH′E-BUC F.Estimating parameters and hidden variables in nonlinear state-space models based on ODEs for biological networks inference［J］.Bioinformatics，2007，23（23）：3209-3216.

［63］BEAUMONT M A，ZHANG W，BALDWIN J D.Approximate Bayesian computation in population genetics［J］.Genetics，2002，162（4）：2025-2035.

［64］SISSON S A，FAN Y，TANAKA M.Sequential Monte Carlo without likelihoods［J］.Proc Natl Acad Sci，2007，104（6）：1760-1765.

［65］TONI T，WELCH D，STRELKOWA N，et al.Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems［J］.J R Soc Interface，2009，6：187-202.

［66］MURPHY K P.Machine learning：a probabilistic perspective［M］.Cambridge：MIT Press，1991.

Precision medicine and big data

GUO Yike1，2，YANG Xian2
（1.School of Computer Engineering and Science，Shanghai University，Shanghai 200444，China；2.Data Science Institute，Imperial College London，London SW7 2AZ，UK）

To achieve precision medicine，collecting and analysing various big data are needed to quantify individual patients.This paper first discusses the need of using data from molecular level to pathway level and also incorporating medical imaging data.Different preprocessing methods should be developed for different data type，while some postprocessing steps for various data types，such as classification and network analysis，can be done by a generalized approach.From the perspective of research questions，this paper then studies methods for answering five typical questions from simple to complex.These questions are detecting associations，identifying groups，constructing classifiers，deriving connectivity and building dynamic models.

precision medicine；big data；analysis methods

TP 311.13

A

1007-2861（2016）01-0017-11

10.3969/j.issn.1007-2861.2015.05.015

2016-01-12

郭毅可（1962—），男，教授，博士生導師，博士，研究方向為大數據.E-mail:y.guo@imperial.ac.uk