基于ε-SVR的用戶視聽在線人數預測

顧純棟（上海大學計算機工程與科學學院，上海200444）

基于ε-SVR的用戶視聽在線人數預測

顧純棟
（上海大學計算機工程與科學學院，上海200444）

預測視聽在線人數能夠幫助廠商提供有價值的信息，獲取更大效益.從時間序列分析出發，經過特征調整，利用支持向量回歸對用戶視聽在線人數進行準確預測.首先，對數據進行時間序列分析建模并預測；然后，將模型視為線性回歸對用戶視聽在線人數作進一步改進，結合時間與實際生活中的特征進行調整，并添加了新的特征；接著，對新特征組成的樣本進行支持向量回歸，通過社會認知優化尋找徑向基函數中的最優參數；最后，得到比較理想的預測效果.

自回歸滑動平均模型；線性回歸；支持向量回歸

多媒體視聽點播是現今生活中主流的娛樂方式之一，也是非常重要的一種信息傳播媒介.與傳統電視臺串行連續流（serial continuous flow）不同，觀眾可以通過點播自由選擇需要觀賞的視聽節目，而不受播出時間的限制，并通過機頂盒等設備記錄此類多媒體視聽點播數據.

點播平臺在線人數和傳統收視率調查數據相比，受眾的偏好等主觀因素已經反映在其主動選擇點播的節目內容中，因而在線人數的記錄已經不再含有主觀偏好因素.主要原因在于此類視聽內容已經不再是連續流播放模式，而是以數據庫的形式存儲并播放，可默認視聽內容在數據庫中保持較恒定的狀態，即單一用戶的選擇不受時間限制，在機頂盒打開的前提下，用戶在線時長較少受到其對節目內容喜好變化的影響.相比節目內容，在線人數的數據變化更加依賴時間走勢，因此在線人數數量能從一定程度上反映出人們的生活作息、點播平臺活躍情況等有價值的信息.預測未來的在線人數能為廠商提供有效的商業決策依據，調整點播內容，并且對當前平臺流量占用情況及時偵測并預警，合理控制擁塞風險，以更好地為用戶提供服務，從而獲取更大效益.

同時，若需評估基于用戶偏好的收視趨勢，則可以基于某個特定收視內容的數據記錄，通過橫向比較，以及從此類海量數據入手挖掘相應的時間段、年齡段、地域段等的潛在關系，最終得出不同收視內容對用戶吸引力的評價指數（evaluation index，EI），從而為制作商提高節目質量提供參考依據.因而，通過機頂盒等設備記錄此類多媒體視聽點播數據，比傳統收視率調查更具主動性、準確性和多樣性.

本研究以上海某公司機頂盒對上海市全市用戶在一定時間段內的記錄數據為樣本，對基于時間軸的在線人數數據進行處理.首先，對原始數據進行清理并獲得每一時刻的在線人數，對在線人數進行時間序列分析建模并預測；然后，將模型視為線性回歸作進一步改進，結合時間與實際生活中的特征進行調整，并添加新的特征；接著，對新特征組成的樣本進行支持向量回歸，通過社會認知優化尋找徑向基函數中的最優參數；最后，得到比較理想的預測效果.

1　模型與方法

1.1時間序列分析

自回歸滑動平均（auto-regressive and moving average，ARMA）模型適用于對平穩序列的預測.ARMA模型把時間序列看作白噪聲殘差與滯后時間序列的線性組合.隨著時間的推移，線性方程中的參數不變，一段連續的白噪聲殘差和數據隨時間向后滑動更新.p階滯后自回歸與q階滑動組合的ARMA（p，q）模型表達式［1］如下：

文獻［2］就使用ARMA模型預測了某電視臺的收視率.針對具有明顯周期性的數據，在ARMA模型上增加季節s滯后時間點就演變成了乘法季節ARMA（seasonal autoregressive and moving average，SARMA）模型，這些時間點具有周期性且可以不連續.乘法季節ARMA（p，q）×（P，Q）S模型表達式如下：

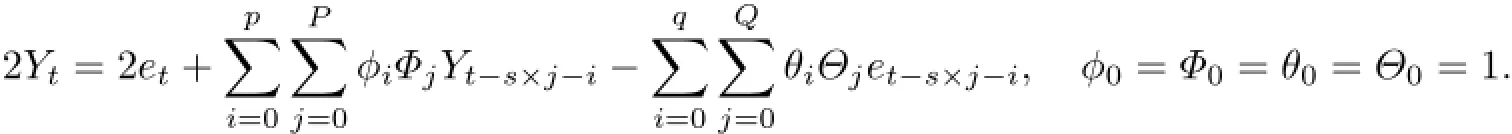
1.2線性回歸

線性回歸（linear regression，LR）是監督式機器學習中的一種基本方法.線性回歸是一組線性方程，數據中的樣本值被視為多個變量的加權和.這些指定的變量被稱為特征向量，線性回歸認為樣本值的大小與這些特征向量有關.從幾何意義上看，這些數據對應的樣本點都在某個多維平面上，通過線性回歸要找到一組與變量對應的最佳參數，使得方程能夠盡可能擬合該多維平面，匹配樣本值.擬合線性回歸可以通過對代價函數求導取極小值，從而得到一個最優解作為參數，具體步驟如下［3］.

已知n×1維樣本向量y，n×d維特征矩陣X，1×d維參數向量θ，n×1維擬合向量y′，則線性回歸方程為

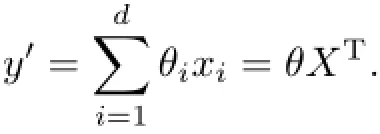
代價函數為

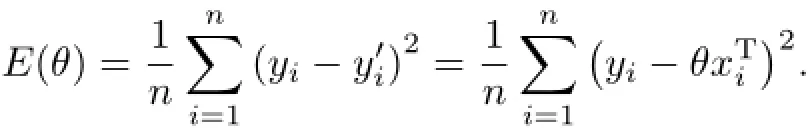
求代價函數E（θ）關于參數向量θ的導數：

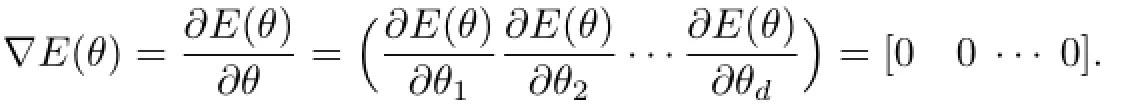
進一步換算可得

從而得到參數向量θ的最優解為

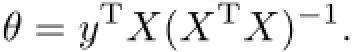
1.3ε-支持向量回歸

支持向量回歸結合支持向量機（support vector machine，SVM）與線性回歸對數據進行擬合.SVM分類器是支持向量的線性組合，通過訓練出的參數來指定哪些向量為支持向量，以及這些支持向量的線性組合方式.由于樣本可能會有噪聲而難免產生誤差，因此在多維擬合平面允許出現一個上下浮動的范圍ε，此模型就稱為ε支持向量回歸（ε support vector regression，ε-SVR）［4］.

與僅最小化現有樣本的誤差不同，支持向量回歸嘗試最小化泛化誤差，以達到更佳的泛化效果.支持向量回歸的思想基于高維特征空間內的線性回歸計算，高維特征空間可以把輸入樣本映射到非線性方程，具體表達式如下：

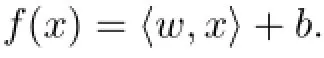
當所有樣本擬合在一個超平面上時，SVM從這些樣本中找到離超平面最近的樣本作為支持向量，并使得支持向量與超平面的距離保持最大.由此可得參數w的優化表達式如下：

參數w的表達式由L2正則化嶺回歸模型演變而來，通過參數C來調整對誤差的懲罰程度.參數w實質是樣本x的線性組合，將參數w分解為βTx，其中x高維度映射的內積可由核函數K（x，x′）完成，轉換后變為最小二乘支持向量機（least-squares SVM，LSSVM），其訓練優化表達式如下：

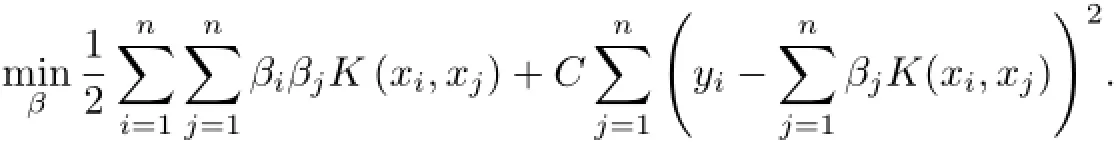
為了稀疏化參數β，由ξ∧和ξ∨表示樣本與超平面的上下偏離程度，從而軟化邊界，并加入寬容度為ε的管道結合KKT（Karush-Kuhn-Tucker）條件來進一步提高容錯，轉換后的模型成為ε-SVR，其訓練優化表達式如下：

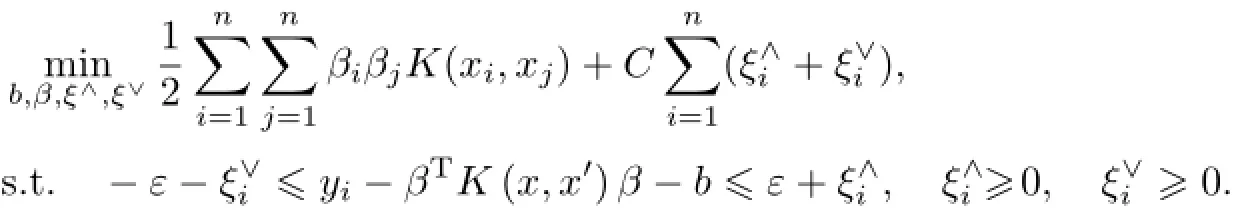
1.4社會認知優化

目前常見的集群智能算法有蟻群算法、遺傳算法、粒子群優化（particle swarm optimization，PSO）算法等.2002年，Xie等［5］設計了一種基于社會認知理論的群集智能優化算法——社會認知優化（social cognitive optimization，SCO）.

SCO算法的步驟如下.

（1）初始化：建立公共知識庫L（library），將nl個隨機生成的待優化樣本作為知識點，另建立ns個社會代理SA（social agent），社會代理擁有自身的知識點.

（2）進入學習周期：每個SA從知識庫L中隨機選取n個知識點進行競爭選擇.

（3）選出的知識點再和SA自身的知識點進行比較，將較好的知識點作為基準點xb，將另一個知識點作為參考點xr.SA基于二者重新生成新知識點xn，生成規則如下：

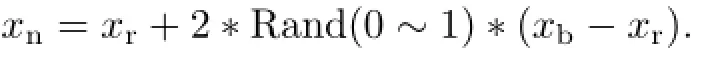
（4）將SA更新的新知識點放回知識庫L.

（5）學習周期完成：更新知識庫L，淘汰掉末尾最差的若干個知識點，一般淘汰的數量與SA的數量相同，然后進入下一輪學習周期.

經過數次循環更新后，知識庫中最優的知識點便是所求最優解.對于一些優化問題的求解，SCO算法在效率與收斂穩定性上比蟻群算法、遺傳算法、PSO算法等都有一定的提高［6］.

2　預測步驟

2.1數據清理

原始數據記錄了每秒用戶的操作日志，并按日期保存在若干文本文件中.數據內容包含用戶設備MAC地址、點播流文件、租看時間、過期時間等信息.數據時間跨度為從2013年1月起的170天.將日志載入數據庫內進行整理，剔除空記錄亂碼等無效數據.將最終數據以每10 min為一組，對此時間段內在線的用戶計數，時間段內無記錄的以零補齊.經過處理后輸出的最終樣本為n×1維向量y，時間跨度為5個月.

2.2模型建立

2.2.1SARMA模型定階

觀察時間序列是否平穩，通過樣本自相關函數（auto correlation function，ACF）檢驗拒絕不存在單位根的零假設，拒絕樣本不平穩假設，由此判斷樣本是平穩的，可以無需拆分而直接使用ARMA模型.觀察樣本的自相關和偏相關系數，根據前300個時間點的樣本ACF（見圖1）可知，樣本拖尾明顯.每隔144個時間點，樣本就會出現一次明顯的強相關，這里假定季節s為144.

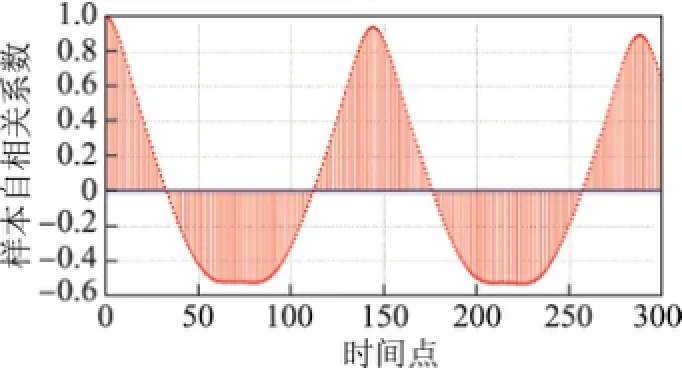
圖1　前300個時間點的樣本ACFFig.1　Sample ACF for 300 time points in front

如圖2所示，每7個假設季節段（1 008個時間點）中，強相關的幅度遵循由高到低再由低到高的周期性變化，每一個周期的起始點由符號“X”標出，由此推斷還存在一個更加廣泛的季節周期，從而得到季節s為1 008.

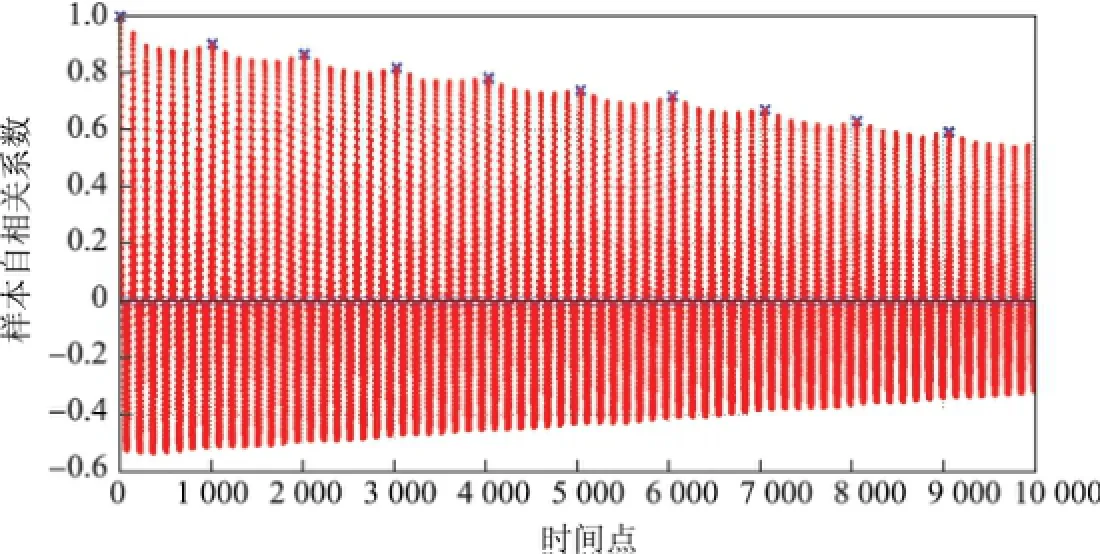
圖2　前10 000個時間點的樣本ACFFig.2　Sample ACF for 10 000 time points in front

根據樣本偏自相關分析函數（partial auto correlation function，PACF）（見圖3）可知，當時間滯后超過5個時間點時，后續樣本的偏自相關系數均不再顯著超過指定閾值，由此可見時間滯后長度為5時PACF值出現了明顯截尾.結合ACF明顯拖尾的情況，給出自回歸（auto-regressive，AR）的階數p為5，滑動平均（moving average，MA）的階數q為0［2］.由此得到定階后的ARMA（5，0）×（1，0）1008模型.

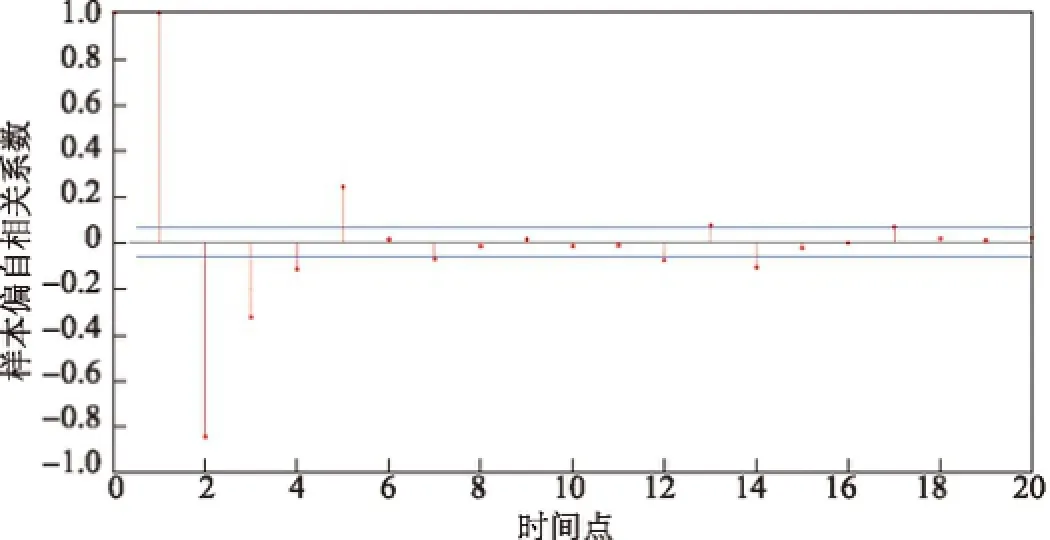
圖3　樣本PACFFig.3　Sample PACF

2.2.2線性回歸模型特征選取

為了更準確地預測數據走勢，除了使用理論模型，還需要與實際情況相結合.ARMA模型只適合平穩數據，所預測的數據只會依照某種規律發生機械性變化，不會考慮到實際情況下的一些不具有明顯時間規律性的因素.而且如果預測時間跨度過大，準確度會出現較大偏差，使用范圍有限.通過觀察發現，可將SARMA模型視為某種線性回歸模型，含有特征向量et，Yt-i，Yt-1 008-i（i∈［0，5］）.增加有效特征向量后，線性回歸的擬合度會明顯上升，可以根據實際情況再添加某些特征向量.這里根據時間特性分別添加了當前數據的日期、時間、節假日信息、每段時間影響因子等特征，具體涵義如下.

x1：日期，當前數據在某月中的第幾天；

x2：小時，24小時制，當前數據在一天中的幾點；

x3：分鐘，時間最小以每10 min為一段；

x4：樣本所在這天是星期幾；

x5：樣本所在這天的屬性，1為正常工作日，2為節假日調整工作日，3為正常雙休日，4為節假日調整休息日；

x6：對應x1影響因子，每月同一天總人數樣本均值；

x7：對應x2影響因子，每天同一小時總人數樣本均值；

x8：對應x3影響因子，每小時同一時間段總人數樣本均值；

x9：對應x4影響因子，每周同一天總人數樣本均值；

x10：對應x5影響因子，同一屬性的時間里總人數樣本均值；

x11：每天變化均值；

x12：每周變化均值.

為提高計算效率，時間序列特征僅保留季節一階滯后Yt-1008，在實際中對準確率造成的影響有限，整個線性回歸模型的特征數為13.

2.2.3ε-SVR模型參數選定

支持向量回歸相比線性回歸有更強的泛化能力來擬合任意函數.本研究選用ε支持向量回歸，核函數K（x，x′）選擇徑向基函數（radical basis function，RBF）對特征向量進行無窮高次冪映射.RBF表達式如下：

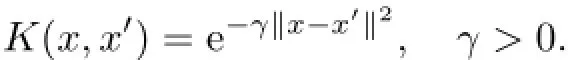
指定懲罰因子C，通過SCO算法尋找最優RBF參數γ［7］，參數γ的優劣評價準則由SVR模型2-fold交叉驗證得到的誤差平方和來決定.在實驗中調整SVR模型參數時發現，雖然懲罰系數C越大，擬合效果越好，但時間代價呈幾何級數增長，擬合度提高程度卻非常有限.參數γ在給定的一個足夠廣的范圍內具有凸優化性質，能夠通過SCO算法在這個范圍內找到全局最優解.但系數C不同，最優參數γ也會不同.最后，通過實驗將參數C確定為1.0×104，模糊邊界ε的上下浮動范圍各為50，將選定模型通過SCO算法優化后得到最優參數γ約為1.7737×10-7.

3　實驗結果

處理后的數據為2013年1月至5月每10 min用戶在線人數的訓練樣本，樣本數約為23000條.通過這些樣本預測2013年6月前7天的在線人數，預測數據量約為1000.原2013 年6月的數據用以檢驗預測結果.在線性回歸和支持向量回歸中，訓練和檢測樣本的特征向量x6，x7，···，x12均只通過訓練樣本產生.已知實際結果y和預測結果y′，模型預測準確度（精確到小數點后兩位）為

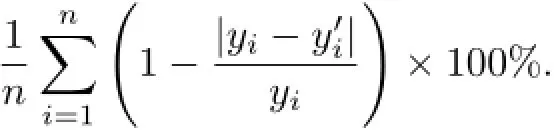
通過ARMA（5，0）×（1，0）1008模型、線性回歸、ε-SVR預測的結果如圖4所示.

圖4　用ARMA（5，0）×（1，0）1 008模型、線性回歸和ε-SVR預測未來一周在線人數Fig.4　Prediction number of online users in next week by ARMA（5，0）×（1，0）1 008model，LR and ε-SVR

從圖4可以看出，3種模型都可以對未來的數據走向作出預測，部分時間段內每個模型的預測值與實際值的差異各有優劣.為了能夠明確作出比較，分別通過平均絕對誤差、準確率等指標計算3種模型預測的準確度（見表1）.

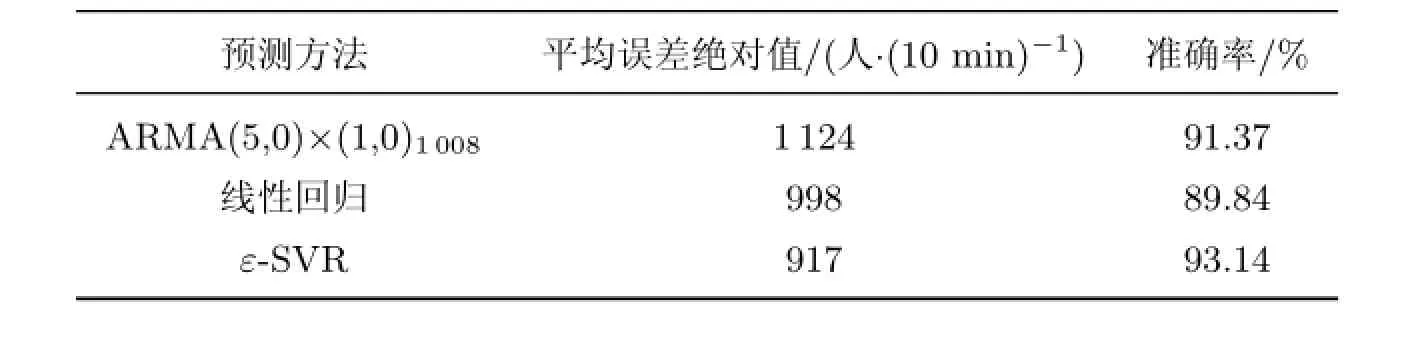
表1　3種模型預測準確度比較Table 1　Comparison of prediction accuracy of three methods

經過計算對比得出，ε-SVR預測出的結果無論在誤差范圍還是準確率上都要優于其他兩種模型.

4　結束語

下面對3種模型進行對比分析.從表達式上不難看出，ARMA模型是一類有著特定特征向量的線性回歸方程.ARMA模型中的預測數據將被作為新樣本特征值，而誤差會成為噪聲存在于新樣本中，隨著時間的推移，噪聲越來越強.雖然一開始有不錯的預測效果，但之后的預測準確度明顯降低，數據的走勢非常機械化.所以，時間序列分析中的ARMA模型只能根據已有數據的走勢來預測短期趨勢［8］.為了減少預測數據和殘差對新樣本的噪聲影響，本研究對原有ARMA模型作出改進，將其視為線性回歸模型，在去除殘差和部分滯后時間序列的基礎上，結合實際情況中的節假日、影響因子等因素增加新的特征向量，而不再拘束于時間序列本身.盡管線性回歸比ARMA模型更能結合實際情況進行預測，但其泛化能力有限.支持向量回歸是一種理想的非線性模型，通過核函數將特征向量映射到高維度空間，結合模糊邊界提高樣本容錯度，在實際應用中取得了較為理想的效果.

對比3種預測方法，除了模型選擇，特征向量的選取也會影響預測效果.雖然本研究基于原始數據對在線人數進行預測，較為充分地考慮了多種與時間有關的變化因素，但部分時間段的預測準確度仍然有比較大的提升空間，推測還可能存在其他原始數據中未能記錄的環境特征變化因素.

［1］CRYER J D，CHAN K S，潘紅宇.時間序列分析及應用：R語言［M］.北京：機械工業出版社，2011.

［2］劉輝，杜秀華.基于ARMA模型的電視臺收視率預測方法設計和實現［J］.控制工程，2009（S1）：9-11.

［3］CHERKASSKY V，MULIER F M.Learning from data：concepts，theory，and methods［M］.NY：John Wiley&Sons，2007.

［4］SMOLA A J，SCH¨OLKOPF B.A tutorial on support vector regression［J］.Statistics and Computing，2004，14（3）：199-222.

［5］XIE X F，ZHANG W J，YANG Z L.Social cognitive optimization for nonlinear programming problems［C］//Proceeding of the First International Conference on Machine Learning and Cybernetics.2002：779-783.

［6］XIE X F，ZHANG W J.Solving engineering design problems by social cognitive optimization［C］// Genetic and Evolutionary Computation—GECCO 2004.2004：261-262.

［7］李童，毛力，吳濱.基于改進PSO優化SVR的交通事故預測模型［J］.計算機與現代化，2014（5）：28-32.

［8］潘紅宇.時間序列分析［M］.北京：對外經濟貿易大學出版社，2006.

Predicting number of online users by ε-SVR

GU Chundong
（School of Computer Engineering and Science，Shanghai University，Shanghai 200444，China）

Predicting the number of online audio-visual users can provide valuable information to help manufacturers get more profits.Based on time series analysis，support vector regression is used to make accurate prediction with adjusted feature.The time series is first modeled and predicted，a linear regression model used to make further improvement，and then，by combining time and real-life characteristics，adding a new feature.Samples of the new feature are trained with support vector regression.Optimal parameters of the radial basis function are sought using the social cognitive optimization.A good prediction result can be obtained using the proposed method.

auto-regressive and moving average（ARMA）；linear regression；support vector regression

TP274；O212

A

1007-2861（2016）01-0097-08

10.3969/j.issn.1007-2861.2015.05.001

2015-11-30

國家自然科學基金青年資助項目（11501352）

顧純棟（1990—），男，碩士研究生，研究方向為數據分析.E-mail:gcd9073@163.com