修正的亥姆霍茲方程的一種解析解法
孔德清
(肇慶學院 電子信息與機電工程學院,廣東 肇慶 526061)
修正的亥姆霍茲方程的一種解析解法
孔德清
(肇慶學院 電子信息與機電工程學院,廣東 肇慶526061)
討論了用于描述波的彌散、擴散等物理現象的修正的亥姆霍茲方程方程的一類邊值問題,借助Fokas變換方法,給出了該問題的解析解.
亥姆霍茲方程;Dirichlet邊值問題;解析解
0 引言
波是一種常見的物理現象,例如聲波、水波、電磁波等.波在傳播過程中遇到障礙物時會產生反射、折射和散射等現象.波的這種特性引發了人們的研究興趣和極大關注,目前,已被廣泛應用于海底探測、醫學診斷、聲納和雷達等領域.研究者通常利用數學方程描述波傳播的各種現象.最著名的方程是1747年由法國著名物理學家、數學家和天文學家達朗貝爾發現的波動方程[1].任何一種特定形式波的傳播均可由數學方程及一定的輔助條件進行刻畫,因此,對于波的各種現象和性態的研究,可轉化為對與其相關的各種數學方程的探討.
1 問題的數學模型
修正的亥姆霍茲方程(modified Helmholtz equation)又稱為Yukawa方程[2],通常出現在半隱式時間離散的熱方程中,也用來描述波的彌散、擴散問題等物理現象[3].多年來,國內外許多研究者都對此方程進行過研究,然而,他們大多采用數值方法進行討論,很少有求得解析解的報道.本文中,筆者在文獻[4]基礎上采用Fokas變換的方法,討論一類平面角形域Ω上修正的亥姆霍茲方程Dirichlet邊值問題的解析解,其數學模型如下:

2 主要結論
為了求解問題(1),首先介紹一個基于Fokas變換的引理.
引理1[5]設Ω為復Z-平面上第1象限所圍成的平面區域,假定在Ω內modified Helmholtz方程存在解,在Ω的邊界上充分光滑,則有如下積分表達式:

其中:譜函數ρ1(k)和ρ2(k)分別定義為
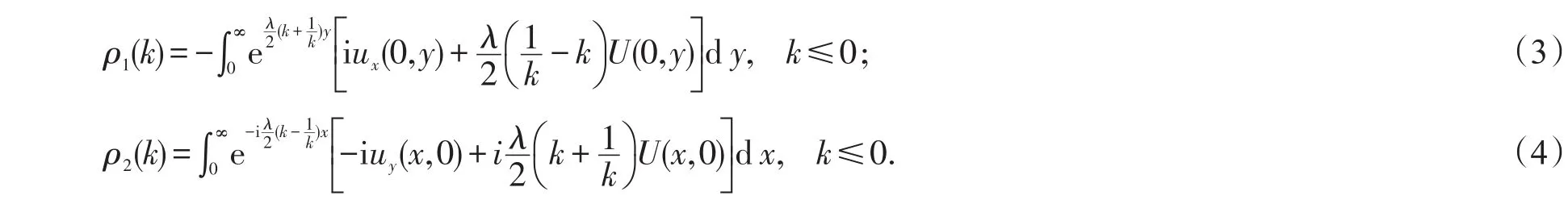
而射線lj(j=1,2)分別表示譜K-平面的正虛軸和正實軸.此外,以下全局關系成立:

事實上,引理1中得到的解的積分表達式(2)是利用譜函數ρj(k)表示的.對于具體問題的定解問題,從式(3)和(4)可以看出,譜函數ρj(k)包含了已知和未知的邊界值,因此,表達式(2)只能算是一種解的形式積分表達式.Fokas變換的思想是利用全局關系(5)提供的邊值變換信息,借助一些對稱關系和復變函數的Cauchy積分定理等,消除積分表達式中的未知量或者求出這些未知量,從而得到定解問題解的封閉積分表達式.
對于問題(1),利用Fokas變換思想可以得到如下定理.

其中:有向射線l1:arg k=π/2;l2:arg k=0,而
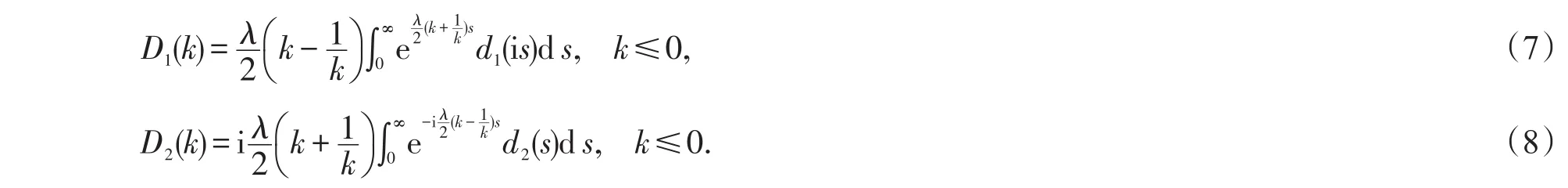
證引入輔助函數

此時,引理1中的ρj(k)(j=1,2)可表示為

容易看出,函數G1(k),D1(k)和G2(k),D2(k)分別為左半K-平面和下半K-平面的解析函數,并且有如下對稱關系:

由全局關系(5),可得

式(15)取復共軛,并考慮到對稱關系,得

即有

由式(15)和(16)可得

令k?-k,經整理可得

因此,由式(6)并考慮到式(17)和(19),可得
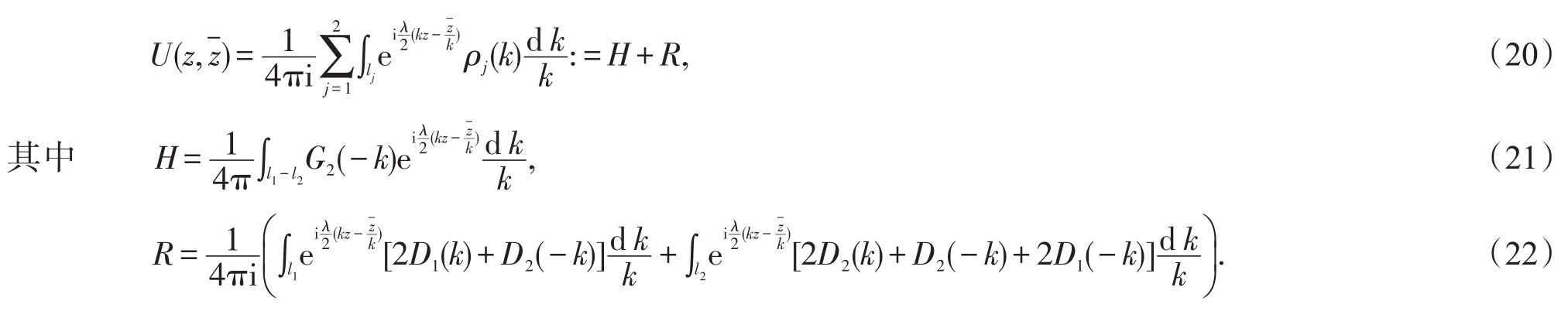
容易看出,利用復變函數的Cauchy積分定理,H等于零.進一步將R中l2上含D2(-k)的項變形成l1上的積分,整理后即得式(6),至此,定理1得證.
[1]谷超豪,李大潛,陳恕行,等.數學物理方程[M].北京:高等教育出版社,2012:2-46.
[2]CHENG H W,HUANG J F,LEITERMAN T J.An adaptive fast solver for the modified Helmholtz equation in two dimensions [J].J Comput Phys,2006,211:616-637.
[3] BEN-AVRAHAM,FOKAS A S,The solution of the modified Helmholtz equation in a wedge and an application to diffusionlimited coalescence[J].Phys LettA,1999,263:355-359.
[4]黃民海.四分之一平面域上Helmholtz方程的混合邊值問題[J].中山大學學報(自然科學版),2011,50(5):7-10.
[5]FOKASAS.Aunified approach to boundary value problems[M].Philadelphia:SIAM,2008:125-184.
An Analytical Solving Method of the Modified Helmholtz Equation
KONG Deqing
(College of Electronic Information and Mechatronic Engineering,Zhaoqing University,Zhaoqing,Guangdong 526061,China)
ractA class of boundary value problems for the modified Helmholtz equation which is used to describe the physical phenomena such as dispersion,diffusion,etc.is discussed,and the analytical solution of the problem is given by means of Fokas transform.
ordsmodified Helmholtz equation;Dirichlet boundary-value problem;analytic solution
O175.2;O175.8
A
1009-8445(2016)02-0001-03
(責任編輯:陳靜)
2015-10-09
孔德清(1963-),男,山東曲阜人,肇慶學院電子信息與機電工程學院副教授,碩士.

