基于短時程突觸可塑性的隨機Hodgkin-Huxely神經元網絡

周家程,　丁少杰,　張雪娟

(浙江師范大學 數理與信息工程學院,浙江 金華　321004)

?

基于短時程突觸可塑性的隨機Hodgkin-Huxely神經元網絡

周家程,丁少杰,張雪娟

(浙江師范大學 數理與信息工程學院,浙江 金華321004)

根據神經元囊泡釋放與離子通道隨機切換的生理學機制,給出一個基于短時程突觸可塑性的隨機HH神經元網絡模型,并討論了通道噪聲與突觸噪聲對網絡發放行為的效應，以及易化與抑制對突觸效能的影響.

突觸可塑性;突觸易化;突觸抑制;網絡模型;HH神經元

0　引　言

神經元的突觸可塑性(synapse plasticity)一般被認為是大腦學習與記憶的分子生物學機制,它是指突觸傳遞效率增強或減弱的變化現象.若這種變化只持續數十毫秒到幾分,便稱之為短時程突觸可塑性(short-term synaptic plasticity).其中:效率增強與減弱分別叫作短時程增強(short-term enhancement)與短時程抑制(short-term depression);而持續數百毫秒的增強又被稱為短時程易化(short-term facilitation)[1].

易化與抑制是2種并存的機制,它們的共同作用對神經系統的信息傳遞起到至關重要的作用.因此,研究短時程突觸可塑性具有重要意義.1998年,Tsodyks等[2]提出了包含易化和抑制2種機制的突觸傳遞模型,構建簡化的神經元網絡,并進行動力學分析;2008年,Mongillo等[3]在上述模型的基礎上構造了一個復雜的Integrate-and-fire神經元網絡,提出了具有工作記憶性的突觸理論;2015年,Romani等[4]又在此基礎上提出了基于短時程突觸可塑性的位置細胞(place cell)網絡模型.

神經元在活動中總受到噪聲的影響.噪聲的來源廣泛, 除了從外界環境信號輸入噪聲外,還包括神經元的通道噪聲(channel noise)及突觸噪聲(synaptic noise)等系統內部存在的噪聲.通道噪聲作為一類重要的噪聲,主要是由離子通道開關的隨機性而產生的[5],常常被用來解釋某些神經元的自發發放現象[6].這使得經典的確定性Hodgkin-Huxely神經元(簡稱HH神經元)模型[7]發展成為由隨機混合系統(stochastic hybrid system)表示的隨機HH神經元模型[8-10].然而,目前并沒有較完善的數值模擬方法和定性分析理論來處理這個隨機混合系統.因而,往往需要將其Langevin近似成一個Gauss噪聲驅動的隨機微分方程組[11-14]以減小問題的復雜性.神經元的自發發放與突觸可塑性一樣,均是生物體內的自組織現象.通過建立數學模型的方法來研究這些現象,可以更清楚地理解這些生物機制,不僅在生理學和醫學領域中對闡明相關大腦疾病(如癲癇、老年癡呆癥、藥物成癮等)的機理有重要意義,而且在人工智能領域中對利用這些自組織現象進行仿生研究提供理論指導.

事實上,文獻[3]提出的神經元網絡過于簡化,未像文獻[15]用α電導來刻畫突觸噪聲,也未像文獻[16-17]考慮通道噪聲與突觸噪聲的共同作用,而文獻[18]提出的短時程突觸可塑性神經元網絡中的α電導只包含抑制機制.因此,本文構建了一個通道噪聲和突觸噪聲共同作用下的HH神經元網絡,并且突觸噪聲基于α電導并同時具有易化和抑制2種短時程突觸可塑性機制.

1　模　型

考慮由N個興奮型HH神經元全連接組成的網絡.根據Kirchhoff電流守恒律得到每個神經元的膜電位的演化方程為

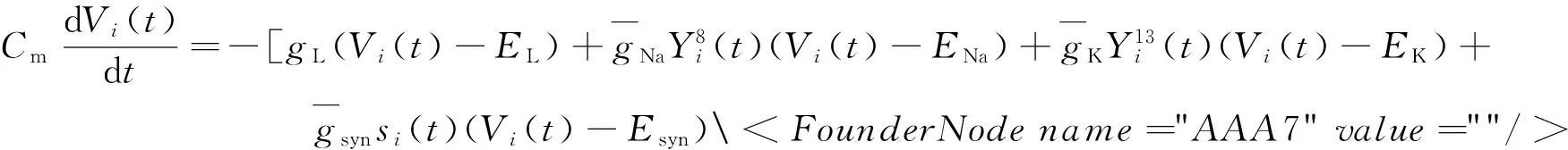
(1)

鈉通道和鉀通道均為電壓門控通道.每個鈉通道由3個相同的m門和1個h門組成,從而具有8種狀態和20種反應,即

(2)

式(2)中,mphq表示只有p個m門和q個h門打開的狀態(p=0,1,2,3,q=0,1).類似地,每個鉀通道由4個n門組成,從而具有5種狀態和8種反應,即

(3)

式(3)中,np表示有p個n門打開的狀態(p=0,1,2,3,4).式(2)和式(3)中的各個狀態和各個反應分別被標記為Sl和Rk(l=1,2,…,13,k=1,2,…,28).當一個離子通道的所有門都打開時,這個通道處于開放狀態.這樣,m3h1(S8)和n4(S13)分別對應鈉通道和鉀通道的開放狀態.需要指出的是,式(2)和式(3)中的反應速率常數{αj,βj}(j=m,n,h)依賴于對應神經元的膜電位,其形式在文獻[7]中給出.定義Yi(t)=(Y1i(t),Y2i(t),…,Y13i(t))T,其中Yli(t)為狀態Sl的通道開放比例,其形式為

其中:Xli(t)為t時刻第i個神經元處于狀態Sl的通道數; NNa=ρNa×S,NK=ρK×S分別是鈉通道和鉀通道的通道總數(ρNa,ρK為相應的通道密度,S為膜面積).易見Yi(t)∈SY,其中

由隨機HH神經元的Langevin近似理論[11-14]可知,Yi(t)的演化可以由如下隨機微分方程近似表示:

(4)

式(4)中,υk為反應Rk的狀態改變向量,滿足

ξki(t)(i=1,2,…,N,k=1,2,…,13)是一簇獨立的標準Gauss白噪聲.另外,函數bk是反應Rk的傾向函數(propensity function),被定義為反應Rk的反應物濃度與相應反應速率常數的乘積[19],如b1(Yi(t),Vi(t))=3αm(Vi(t))Y1i(t).函數σk滿足

網絡中的各神經元通過化學突觸相互連接,其樹突上接收遞質的突觸通道是配體門控的,可用α電導模型來刻畫;釋放遞質的軸突末端具有短時程突觸可塑性.因此,由α電導的微分方程[20]和短時程突觸可塑性模型[3]得到如下突觸動力學模型:

(5)

式(5)中:si(t),hi(t)和τs分別為α電導的突觸通道開放比例,遞質水平變化率和衰退時間常數;ri(t)和ui(t)分別為t時刻神經元軸突末端貯藏的囊泡比例和囊泡釋放概率,滿足0≤ri(t)≤1,u0≤ui(t)≤1,其中ui(t)由突觸末端的殘余鈣離子水平所決定,殘留鈣離子水平越高,ui(t)就越大[3];τD,τF分別為ri(t),ui(t)的衰退時間常數,u0是ui(t)的基準值.另外,δ為Dirac-delta函數;τd為神經遞質傳輸延遲,服從1～5 ms上的均勻分布[3];tki為第i個神經元第k次發放時刻.這樣,ri(t)和ui(t)在tki時刻上的跳躍反映了該神經元遞質的量子式釋放和鈣離子的流入;而hi(t)在tkj+τd時刻上的跳躍代表接收第j個神經元釋放的遞質.

聯立式(1)、式(4)和式(5),構成一個耦合的跳擴散隨機微分方程組,其初值條件如下:對i=1,2,…,N,Vi(0)為-80～-65 mV的均勻分布隨機數;Yi(0)由

且Yi(0)∈SY確定;ri(0)=1;ui(0)=u0.本文采用步長為0.01 ms的前向Euler-Maruyama算法進行數值模擬,進而得到一個離散時刻在0～3 000 ms的近似樣本序列.在模擬中,對Yi的模擬值未落在SY的情形采用文獻[14]給出的方法進行截斷處理,tki是通過設置10 mV的閾值和2 ms的絕對不應期來確定的一個離散時刻.數值模擬的其他參數見表1.

表1　隨機HH神經元網絡參數

2　結　果

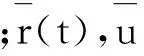
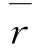
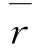
黑點表示神經元的一次發放,虛線和實線分別表示(t)和(t)隨t的變化情況圖1　當τD=200 ms,τF=1 500 ms時不同膜面積下神經網絡的發放情況

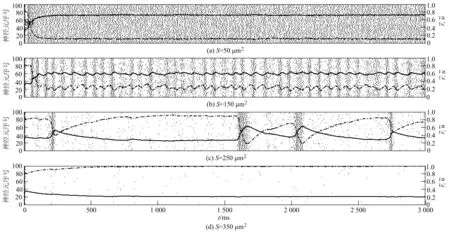
黑點表示神經元的一次發放,虛線和實線分別表示(t)和(t)隨t的變化情況圖2　當τD=200 ms,τF=200 ms時不同膜面積下神經網絡的發放情況

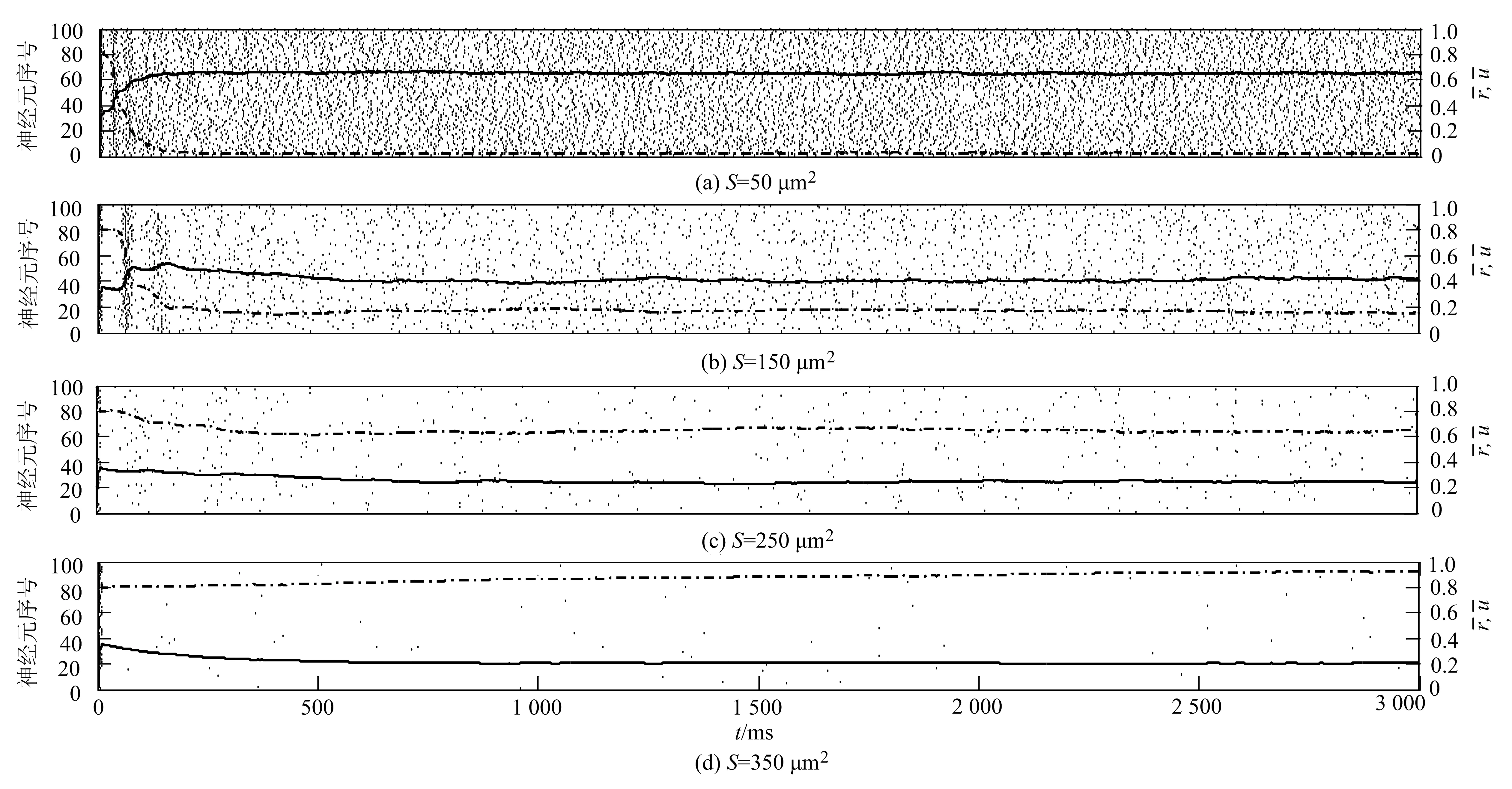
黑點表示神經元的一次發放,虛線和實線分別表示(t)和(t)隨t的變化情況圖3　當τD=1 500 ms,τF=200 ms時不同膜面積下神經網絡的發放情況

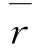
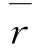
為進一步系統地研究該網絡的性質,需引入發放率R、變異系數CV、同步指數C及突觸效能(synaptic efficacy)E,分別刻畫該網絡的活躍性、時間相干性、空間相干性及突觸可塑性.R,CV和C的定義在文獻[17]中給出,并且R和C越大分別代表網絡的活躍性、空間相干性越好,而更小的CV對應更好的時間相干性.定義E為

其中:T為觀察時間(取為3 000 ms);r(tki)u(tki)是第i個神經元在第k次發放釋放的囊泡比例.易見,E越大,網絡的突觸傳遞效率越高.上述4個指標通過20次獨立重復的數值模擬的平均結果來估計.下面分別取S值為50,150,250,350 μm2,研究不同的τD和τF值對R,CV,C和E的影響 (見圖4).

首先比較圖4(a).R在區域中的最大值隨著S值的增大而減小.當S=50 μm2時,R隨τF變化基本保持不變,但可以隨著τD增大而增大,并趨于某個水平;當S=150,250 μm2時,τF越大,R越大,τD越大,R越小;當S=350 μm2時,R在大部分區域小于1 Hz,僅在τF?τD的部分超過1 Hz.

接著比較圖4(b).E在區域中的最大值在S值較大時處于較高水平.當S=50,150 μm2時,若τD小于某個水平,則τF的增大會引起E增大,τD的增大會導致E減小;當S=250,350 μm2時,這種現象幾乎在整個區域都會出現.值得注意的是,當S=350 μm2時,E與τD,τF接近線性關系.

最后,分別比較圖4(c)和圖4(d).當S=50 μm2時,τF不會影響CV和C,但τD的增大卻可以導致CV的增大和C的減小;當S=150,250 μm2時,需要在τD較小時,隨著τF變化CV和C才會出現明顯變化;當S=350 μm2時,CV和C在R較小的區域內數值較低,在R較大的區域內數值較高.

(a),(b),(c)和(d)4列分別對應網絡的R,E,CV和C在不同S下關于τD,τF的變化;第1～4行分別表示面積S=50,150,250,350 μm2圖4　不同S,τD,τF對網絡性質的影響

3　討　論

本文構造了一個由通道噪聲和突觸噪聲驅動的全連接的HH興奮型神經網絡,并且在突觸噪聲中通過引入突觸變量ri(t),ui(t)來反映短時程突觸可塑性.進一步分析模擬結果并結合生物意義可知,τD和τF分別反映了突觸可塑性的抑制和易化強度.在網絡中,τD值越大,對神經元發放的抑制效果越強,而τF值增加可以促進神經元發放.具體見圖1和圖3.

上述結論也可從式(5)得出:若τD值越大,則ri(t)上升趨于1的速率越慢,其中ri(t)表示突觸末端貯藏的囊泡比例.貯藏的囊泡個數始終保持較低的值,導致每次釋放的囊泡數量較少,從而抑制神經元發放.類似地,若τF值越大,則ui(t)下降趨于u0的速率越慢,其中ui(t)表示突觸末端囊泡釋放的概率.囊泡始終保持較高的釋放概率,致使突觸后神經元接收的神經遞質的量增加,從而促進神經元的發放.

圖4的結果說明:當τD足夠小且S值適中時,τD和τF的增加可以分別降低和增加網絡的活躍性、時空相干性和突觸傳遞效率.由式(4)可知,S值與通道噪聲的強度成反比.在S=50 μm2的情形中,通道噪聲過強,使得τF對4個指標的影響不明顯,但τD仍能影響這4個指標;在S=350 μm2的情形中,通道噪聲較弱,網絡發放不頻繁,使得τD和τF的變化均不能顯著影響網絡的活躍性和時空相干性,但是E仍可受到τD和τF影響,并且由于過少的發放使得ri(t)和ui(t)維持在一個平穩水平,從而使這種影響呈現一種接近線性的關系.同時發現,即使通道噪聲減弱,短時程抑制的存在仍可以破壞網絡的發放同步性.因此,突觸可塑性使得突觸噪聲與通道噪聲協同作用更為復雜多樣.

[1]Zucker R S,Regehr W G.Short-term synaptic plasticity[J].Annu Rev Physiol,2002,64(1):355-405.

[2]Tsodyks M,Pawelzik K,Markram H.Neural networks with dynamic synapses[J].Neural Comput,1998,10(4):821-835.

[3]Mongillo G,Barak O,Tsodyks M.Synaptic theory of working memory[J].Science,2008,319(5869):1543-1546.

[4]Romani S,Tsodyks M.Short-term plasticity based network model of place cells dynamics[J].Hippocampus,2015,25(1):94-105.

[5]Hamill O P,Marty A,Neher E,et al.Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches[J].Pflügers Archiv,1981,391(2):85-100.

[6]Hille B.Ion channels of excitable membranes[M].Sunderland:Sinauer Associates,2001.

[7]Hodgkin A L,Huxley A F.A quantitative description of membrane current and its application to conduction and excitation in nerve[J].J Physiol,1952,117(4):500-544.

[8]Skaugen E,Wall?e L.Firing behaviour in a stochastic nerve membrane model based upon the Hodgkin-Huxley equations[J].Acta Psychiatr Scand,1979,107(4):343-363.

[9]Clay J R,Defelice L J.Relationship between membrane excitability and single channel open-close kinetics[J].Biophys J,1983,42(2):151-157.

[10]Chow C C,White J A.Spontaneous action potentials due to channel fluctuations[J].Biophys J,1996,71(6):3013-3033.

[11]Fox R F,Lu Y.Emergent collective behavior in large numbers of globally coupled independently stochastic ion channels[J].Bakhtiniana Revista De Estudos Do Discurso,2012,7(49):3421-3431.

[12]Pakdamank K,Thieullen M,Wainrib G,et al.Fluid limit theorems for stochastic hybrid systems with application to neuron models[J].Adv App Probab,2010,42(3):761-794.

[13]Goldwyn J H,Imennov N S,Famulare M,et al.Stochastic differential equation models for ion channel noise in Hodgkin-Huxley neurons[J].Phys Rev E,2011,83(4):041908.

[14]Huang Yandong,Rüdiger S,Shuai Jianwei.Langevin approach for stochastic Hodgkin-Huxley dynamics with discretization of channel open fraction[J].Phys Lett A,2013,377(44):3223-3227.

[15]Yu Y,Liu F,Wang W.Synchronized rhythmic oscillation in a noisy neural network[J].J Phys Soc Japan,2003,72(12):3291-3296.

[16]Chen J,Ding S,Li H,et al.Synchronization and array-enhanced resonances in delayed coupled neuronal network with channel noise[J].Chaos:An Interdisciplinary Journal of Nonlinear Science,2014,24(3):033131.

[17]Zhang X,Li H,Chen J,et al.The impact of channel and external synaptic noises on spatial and temporal coherence in neuronal networks[J].Neurocomputing,2015,164:230-239.

[18]Sakumura Y,Ishii S.Stochastic resonance with differential code in feedforward network with intra-layer random connections[J].Neural Networks,2006,19(4):469-476.

[19]Gillespied D T.A rigorous derivation of the chemical master equation[J].Physica A:Statistical Mechanics and its Applications,1992,188(1):404-425.

[20]Destexhe A,Mainen Z F,Sejnowski T J.Synthesis of models for excitable membranes, synaptic transmission and neuromodulation using a common kinetic formalism[J].J Comput Neurosci,1994,1(3):195-230.

(責任編輯陶立方)

Short-term synaptic plasticity based network of stochastic Hodgkin-Huxely neurons

ZHOU Jiacheng,DING Shaojie,ZHANG Xuejuan

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,Jinhua321004,China)

According to the physiological mechanism of the vesicle release and random switching of ion channels, a short-term synaptic plasticity based network model of stochastic Hodgkin-Huxely neurons was proposed. The effect of the channel noise and the synaptic noise on the firing behavior of the network and the influence of facilitation and depression to synaptic efficacy were discussed.

short-term synaptic plasticity; facilitation; depression; network model; Hodgkin-Huxley neuron

10.16218/j.issn.1001-5051.2016.03.006

收文日期：2015-09-06；2015-11-26

周家程(1992-),男,浙江臺州人,碩士研究生.研究方向:計算神經科學.

張雪娟.E-mail: xuejuanzhang@gmail.com

O211.63;Q332

A

1001-5051(2016)03-0268-08