基于熱彈耦合的渦輪轉子瞬態熱沖擊研究

徐寧，王慶超1，劉占生1，楊帆1

（1.哈爾濱工業大學能源科學與工程學院，黑龍江哈爾濱150001；2.中船重工第703研究所，黑龍江哈爾濱150078）

基于熱彈耦合的渦輪轉子瞬態熱沖擊研究

徐寧1，2，王慶超1，劉占生1，楊帆1

（1.哈爾濱工業大學能源科學與工程學院，黑龍江哈爾濱150001；2.中船重工第703研究所，黑龍江哈爾濱150078）

渦輪轉子在瞬態熱沖擊下的熱應力是最重要的參數之一，它直接影響著轉子的疲勞壽命以及運行的安全性。基于熱彈耦合理論推導和有限元數值仿真，針對渦輪轉子的兩種典型結構開展了瞬態熱沖擊下的熱分析，研究了瞬態應力場、溫度場的分布特性及其隨轉子結構參數的變化規律。同時，針對渦輪轉子在實際工作過程中常遇到的非對稱熱沖擊現象，進行了轉子在周向非對稱熱沖擊載荷分布下的熱分析，研究結果表明渦輪轉子瞬態熱應力大于穩態熱應力，且受到倒圓半徑、輪盤厚度和盤軸比的影響，研究結果對發動機轉子設計初期的熱疲勞壽命評估有借鑒意義。

瞬態熱沖擊；渦輪轉子；熱應力；非對稱熱載荷；熱疲勞壽命

當代戰爭要求武器裝備在戰備狀態及應急突發事件時，能夠以不惜犧牲部分發動機的熱疲勞壽命來實現最短時間內的快速啟動。而這種不計代價的快速啟動方式，將使艦船發動機的渦輪轉子無法經歷暖機過程，而在最短的時間內快速達到運行工況，進入流道的氣流溫度與轉子金屬表面間存在較大的溫度梯度，導致轉子承受著巨大的熱沖擊。而由于渦輪盤常工作在復雜非均勻的熱載荷環境下，極易產生熱疲勞積累而導致轉子總應力增加及材料性能惡化［1］。因此，對艦船發動機渦輪轉子的熱分析應側重熱沖擊及非對稱熱載荷分布下的瞬態熱應力變化及溫度分布特性研究。

國內外學者關于發動機轉子的熱應力分析側重理論計算［2-4］和在線監測［5-8］兩方面。而對于轉子的瞬穩態溫度場、熱應力計算方面的研究主要是建立理論解析模型［9-11］和有限元數值仿真［12-14］，其中理論解析模型正是通過求解熱傳導方程和彈性理論控制方程得到熱變形及熱應力，并建立普遍形式的轉子熱應力求解方程，這樣能夠較為簡便地給出溫度分布下的熱變形及熱應力，多適用于在線監測中熱疲勞壽命的快速預測分析。而有限元數值仿真是基于數值法解決基本傳熱方程和彈性理論，它是一種能夠有效準確地分析各種復雜結構和邊界條件的方法。回顧近年來研究人員在進行發動機轉子的熱分析來看，有限元法數值仿真結果與在線實測結果也更加接近［15］。而其缺點就是計算工作量較大、需要驗證仿真結果的精確性。

事實上，瞬態熱沖擊載荷是影響轉子壽命的關鍵，而針對瞬態熱沖擊下發動機轉子典型結構參數及熱沖擊載荷邊界對熱應力和溫度場的影響研究卻不多。同時，針對發動機轉子在實際工作中受到的周向非對稱熱載荷的問題，如燃燒室火焰筒點火不均勻、熄火等故障，渦輪盤將承受局部熱沖擊載荷，極易導致轉子發生熱變形，最終嚴重影響轉子熱疲勞壽命并產生熱致振動現象，這方面研究也較缺乏。因此，本文基于熱彈耦合理論建立了轉子熱沖擊理論計算及有限元分析模型，研究周向均布和非對稱兩種熱沖擊載荷下渦輪轉子的最大熱應力變化和溫度場分布特性，為艦船發動機方案設計初期的熱疲勞壽命預估提供有意義的借鑒。

1　轉子主軸結構—熱分析模型

轉子主軸的瞬態熱分析建模，將采用基于熱傳導方程和彈性理論推導出的理論方法。假設轉子主軸外表面溫度為Tb，初始溫度分布為T0，轉子外徑大小為b，假設溫度分布沿軸向及周向均勻分布，即溫度T函數僅是半徑r的函數，如圖1所示。

圖1　轉子主軸分析模型示意圖Fig.1 Illustration of the analyzed shaft model

1.1主軸結構熱傳導分析

上述問題可以描述為一維徑向導熱問題，引入過余溫度函數:

圓柱坐標系下無熱源的熱傳導控制方程為

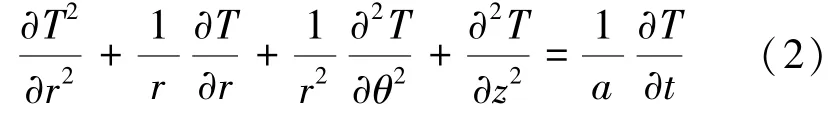
式中:a為熱擴散率，m2/s。引入過余溫度函數的一維導熱問題，式（2）可以簡化為

采用過余溫度函數表示的第一類溫度邊界以及條件初始條件可以表示為

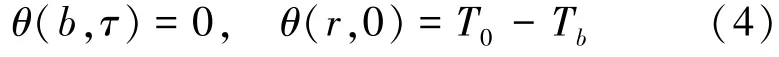
運用數學物理方法中分離變量的方法，可將θ（r，τ）分解成關于時間項及空間項特征函數:

其中，時間項特征函數特解形式為

空間項特征函數解的表達式為

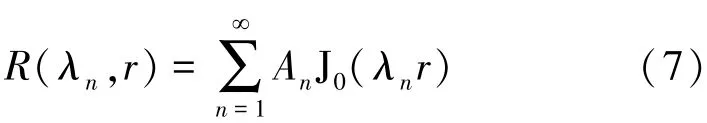
因此過余溫度函數可以整理成:

聯立式（4）、（8），可以得到關于特征值λn以及系數An的方程:

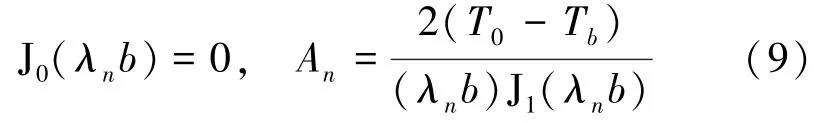
故轉子主軸結構瞬態溫度場函數的表達式為

式中:Jn（λnr）為貝塞爾函數，λn為貝塞爾函數特征值。

1.2主軸結構熱彈耦合分析

由于轉子的軸向尺寸比另外兩向要大得多，故可等效為平面應變問題。根據平面應變理論有

圓柱坐標系下的運動平衡微分方程:

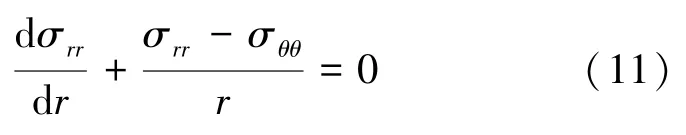
幾何方程:

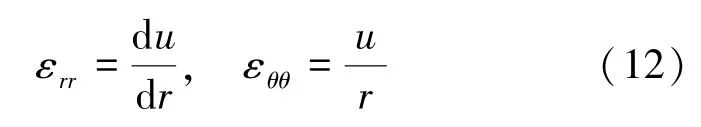
物理方程:

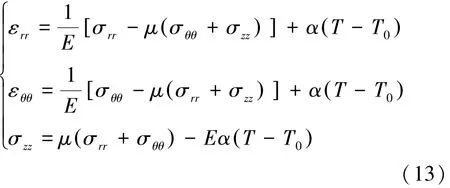
聯立式（10）、（13），得到轉子柱坐標系下瞬態熱應力分量如下

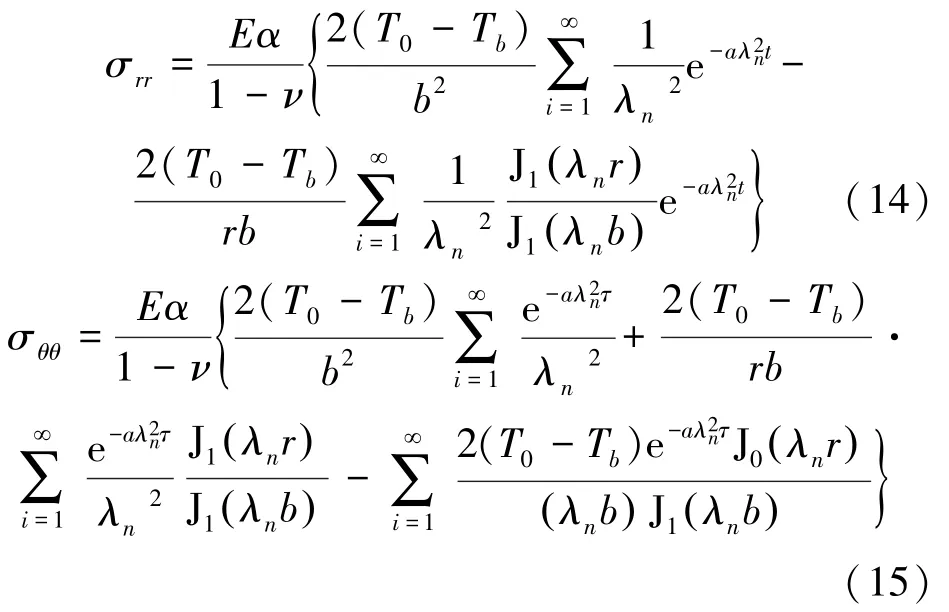
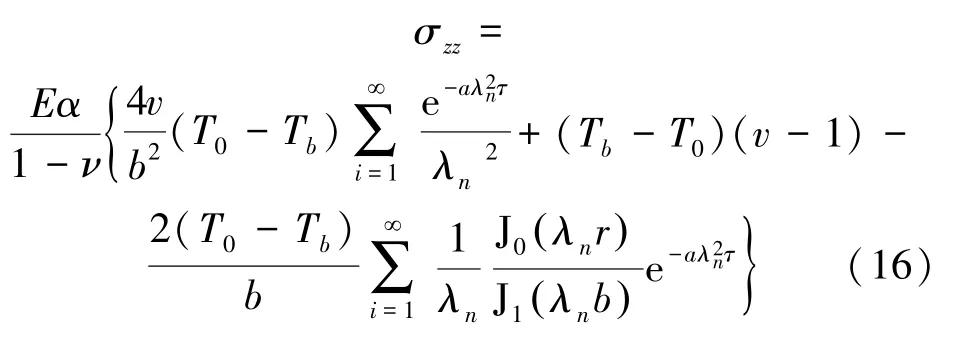
而米塞斯應力常作為衡量透平機械強度的準則，可通過下式求解:

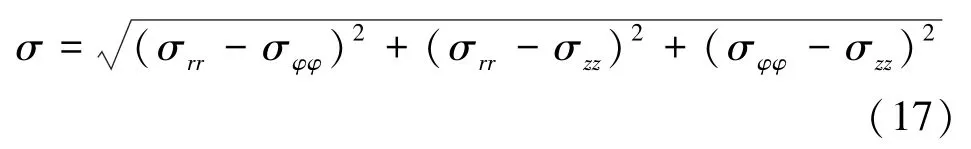
1.3有限元仿真分析

為驗證轉子瞬態溫度場及熱應力場的理論模型，對比了有限元數值仿真結果。主軸模型共劃分400個溫度—位移耦合單元，并完成了網格密度及時間步長的無關性驗證，二者之間的誤差在5%以內，證明了本文軸單元熱分析模型的準確性。

圖2為瞬態熱沖擊載荷下圓柱體主軸的瞬態徑向、周向和軸向熱應力，以及瞬態溫度場的變化情況，同時對比了有限元計算結果。

圖2（a）所示徑向熱應力在初始階段急劇增大，最大徑向熱應力隨半徑發生變化，隨著半徑的增加，最大徑向熱應力逐漸減少。在達到最大值后，徑向熱應力隨時間的增加而減小到0。如圖所示，對比在r=0，r=0.5b，r=0.75b和r=b處的徑向應力兩者之間的平均徑向應力誤差在1.03%，式（14）的理論結果與有限元結果是一致的。由于式（14）中半徑在分母上，r=0理論上是徑向熱應力分析的奇點線，但有限元可以給出結果。在r=b處，式（14）預測的結果比有限元結果小，其他位置公式二者擬合的很好。

圖2　瞬態熱分析結果與有限元分析結果對比Fig.2 Comparison of the thermal analyses with finite element analyses

圖2（b）給出了周向熱應力分量。在中心附近位置是拉應力，而在軸外表面附近變成了壓應力。式（15）預測周向熱應力要大于有限元法，兩者的誤差不大于2.35%。半徑處由于開始階段外表面溫度梯度較大，在初始階段對外表面的網格質量要求高，而有限元模型結果受限于軸表面處的網格尺寸，而理論方法卻沒有這個問題。隨著軸表面單元的徑向尺寸減小，有限元結果更接近于理論解。

軸向熱應力分布如圖2（c）所示。軸向熱應力的分布規律與周向相似。軸向熱應力隨時間逐漸接近一個定常的壓應力，周向熱應力逐漸變成0。對比式（16）的理論結果和有限元結果，兩種方法的軸向熱應力結果一致，大部分位置誤差不大于0.5%。式（16）和有限元法的差別發生在初始階段的外表面。誤差在于軸表面單元的徑向尺寸。

圖2（d）比較了兩種方法的瞬態溫度分布結果。徑向溫度分布開始迅速變化，這是由內外徑巨大的溫差引起的。徑向溫度分布隨時間變化逐漸減慢。幾分鐘后，溫度分布恒定。式（10）的結果與有限元結果保持一致，兩者之間的誤差不大于1%，證實了理論模型的正確性。

圖2（e）比較了式（17）和有限元法計算的米塞斯應力，由于在位置r=0和r=b處的應力分量的不同，米塞斯應力的差別在這兩處比較明顯。對于理論分析來說，軸線處是奇異的，理論方法無法求解。但軸表面的理論結果要比有限元法更精準，特別在瞬態傳熱徑向溫度梯度很明顯的初始階段。為了仿真瞬態熱應力更準確，有限元法需要在軸表面處更優良的網格質量。

通過比較理論解與有限元仿真結果可以發現，圓柱體主軸的瞬態溫度場分布及三維瞬態熱應力變化規律基本一致，驗證了理論解的準確性。

2　結構參數對輪盤根部倒圓結構的影響熱分析

輪盤根部倒角是由主軸和輪盤構成的，是渦輪轉子最普遍的一種結構形式。一般來講，倒角處的熱應力要遠遠大于其他位置，因此將采用有限單元模型對倒角處溫度分布及熱應力進行數值仿真析。

圖3　輪盤根部倒圓角結構示意圖Fig.3 Illustration of the disk corner structure

倒角結構如圖3所示，倒圓角是由軸半徑b和盤半徑D形成的，倒角的半徑為R，倒角結構的初始溫度為T0，外表面的邊界溫度是Tb。理論上，由于倒圓角結構的奇異性，很難通過理論分析獲得其熱應力。故該處熱應力將通過有限元法進行研究。材料屬性與之前的研究保持一致。由于倒角處的熱應力明顯大于其他部位，因此該處的網格應更優良。分析前驗證了網格密度和時間步長的無關性，二者差別不大于1.8%，證明了分析模型的準確性。倒角網格局部細化模型如圖4所示。

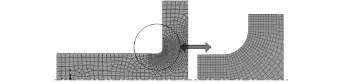
圖4　輪盤根部倒圓角處網格局部細化Fig.4 Local refined mesh at the disk corner

倒圓半徑R=1 mm的模型，輪盤根部倒圓角處的最大瞬態熱應力值隨時間變化趨勢如圖5。可以看到在受到瞬態熱沖擊后，熱應力在初始階段快速增加，轉子的最大瞬態熱應力發生在44 s左右，峰值過后熱應力逐漸減小并趨于穩定值。

倒圓半徑明顯的影響最大熱應力，取一系列同軸徑、盤徑，但不同倒圓角半徑（1 mm～30 mm）的模型進行研究和比較，如圖6（a）所示。不同倒圓半徑之間的熱應力相差比較明顯，最大熱應力從2 338 MPa（R=1 mm）減小到 731.5 MPa（R= 30 mm）。增加倒圓半徑，是減小倒角處熱應力的有效方法。

將軸徑與盤徑之比簡化成β=D/b，研究不同倒圓角R下的熱應力隨β的變化規律。結果如圖6 （b），對相同倒圓半徑下的模型，在盤軸徑比β＜1.4時，熱應力隨β而增加。當盤軸徑比β＞1.4時，熱應力值逐漸降低到常值。不同模型的熱應力在不同倒角時具有同樣的變化趨勢。

圖5　輪盤根部倒角處的最大熱應力隨時間變化圖Fig.5 Variation of maximum thermal stress at disk corner with time

當盤軸徑比在 β=1.5時，倒圓半徑為 R= 1 mm，3 mm，5 mm，7 mm，10 mm熱應力隨軸徑的變化規律如圖6（c）。隨軸徑的增加，熱應力幾乎不變。不同倒圓半徑具有相同的結果。

圖6（d）給出了不同輪盤厚度下的熱應力，當軸徑b=50 mm，盤軸徑比β=1.5，倒圓半徑R=5 mm時，研究輪盤厚度對倒角最大熱應力的影響。倒角最大熱應力隨輪盤厚度的增加而增大。

圖6（e）給出了不同盤軸徑之比下最大熱應力發生時間隨倒圓半徑的變化。可以看到發生時間隨盤軸徑之比增加而增加，同時增加變得的越來越慢。在同樣的盤軸徑之比下，發生時間隨小β值增加而緩慢增加。然而在大β值下增加的更加明顯。在盤軸徑之比不變下，最大熱應力發生時間隨倒圓半徑的變化。隨倒圓半徑的增加，發生時間急劇增加。倒圓半徑越大，出現時間越久。

綜上，倒圓角半徑對轉子最大熱應力的影響較大，隨倒圓角的增加最大熱應力將會大幅度降低；輪盤與軸的半徑比對最大熱應力有一定的影響；主軸的半徑對最大熱應力的影響不大；輪盤厚度的增加將會增大最大熱應力。

圖6　結構參數對最大熱應力及其發生時間的影響Fig.6 Influence of the structure parameters on the maximum thermal stress and the happening time

3　渦輪轉子非對稱熱沖擊研究

燃燒筒點火不均勻及運行時出現故障，會導致燃機渦輪盤承受瞬態非對稱熱載荷。這類問題屬于周向非對稱邊界問題，即在轉子某一扇區（1/6，2/6，…，5/6）加載瞬態熱沖擊載荷，其與周圍扇區的溫差驟升，在此情況下對轉子進行瞬態熱沖擊分析。研究對象取經過適當簡化后的某型燃機渦輪端轉子。初始條件及邊界條件用數學模型可表示為

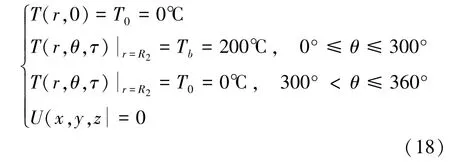
通過對渦輪轉子表面不同扇區大小進行等溫差熱沖擊，發現轉子最大熱應力發生位置位于渦輪盤熱沖擊扇區表面與軸交界的倒角處，在一分鐘內輪盤最大熱應力水平隨時間的變化規律如表1。

表1　各扇區角度對應的最大熱應力值Table 1 The maximum thermal stress under different angles of section

如圖7，輪盤熱應力值在前十秒快速增長并達到極值，而后緩慢降低，其中5/6扇區的升高速率最快且熱應力值也最大，而后50 s最大應力逐漸降低，熱沖擊扇區的角度越大，對渦輪的強度越不利。

圖8表明:熱沖擊扇區越大，溫度場、應力場分布越趨于均勻，且平均應力水平逐漸增大，對轉子安全性的影響增大；同時，熱應力值較大的危險區域主要集中在輪盤與軸結合的倒角的一定范圍內。

4　結論

本文基于導熱控制方程以及彈性力學對渦輪轉子兩種典型結構的瞬態熱應力進行了研究，主要結論包括:

1）瞬態最大熱應力水平遠遠高于穩態結果，倒圓半徑越大，瞬態熱應力降低越明顯，輪盤厚度及盤軸比會影響最大熱應力的大小，而主軸半徑對其幾乎不影響。

2）瞬態熱沖擊下，渦輪轉子的最大熱應力出現時間主要與主軸半徑有關，盤軸比對其略微有影響。

3）渦輪轉子瞬態在非對稱熱沖擊下的最大熱應力開始快速增大并達到極值，而后緩慢減小，非對稱熱沖擊的扇區越大，應力極值越大。

熱沖擊下的瞬態熱應力分析結果對渦輪轉子結構設計初期評估熱疲勞壽命提供有意義的參考。

［1］BUNKER R S.Gas turbine heat transfer:10 remaining hot gas path challenges［J］.Journal of turbomachinery，2006，129（2）:193-201.

［2］VULLO V，VIVIO F.Elastic stress analysis of non-linear variable thickness rotating disks subjected to thermal load and having variable density along the radius［J］.International journal of solids and structures，2008，45（20）: 5337-5355.

［3］呂智強，韓萬金.采用熱流法計算汽輪機轉子表面熱應力［J］.動力工程，2005，25（6）:765-769. LYU Zhiqiang，HAN Wanjin.Calculation of thermal stress on steam turbine rotor surfaces by the heat flux method［J］. Journal of power engineering，2005，25（6）:765-769.

［4］BHATTI S K，KUMARI S，NEELAPU M L，et al.Transient state stress analysis on an axial flow gas turbine blades and disk using finite element procedure［J］.WSEAS transactions on heat and mass transfer，2006，1（3）:329.

［5］MUKHOPADHYAY N K，DUTTA B K，KUSHWAHA H S. On-line fatigue-creep monitoring system for high-temperature components of power plants［J］.International journal of fatigue，2001，23（6）:549-560.

［6］MUKHOPADHYAY N K，DUTTA B K，KUSHWAHA H S，et al.On line fatigue life monitoring methodology for power plant components［J］.International journal of pressure vessels and piping，1994，60（3）:297-306.

［7］ANTONIO C P，LUIS S R，JESUS N G，et al.Integration of thermal stress and lifetime supervision system of steam turbine rotors［J］.Proceedings of the ASME turbo expo，2008 （2）:1035-1044.

［8］劉占生，黃世勇.汽輪機轉子熱應力在線監測與疲勞壽命分析［J］.汽輪機技術，2008，50（1）:9-12，28. LIU Zhansheng，HUANG Shiyong.The turbine rotor thermal-stress online monitor and fatigue life analysis［J］.Turbine technology，2008，50（1）:9-12，28.

［9］武新華，宋春汀，張新江，等.汽輪機轉子熱應力簡化計算公式的選取［J］.汽輪機技術，2000，42（1）:20-23. WU Xinhua，SONG Chunting，ZHANG Xinjiang，et al.Selection of reduction formula in computing turbine rotor thermal stress［J］.Turbine technology，2000，42（1）:20-23.

［10］SONG G，KIM B，CHANG S.Fatigue life evaluation for turbine rotor using green＇s function［J］.Procedia engineering，2011，10:2292-2297.

［11］ZHANG Chunlin，HU Niansu，YANG Wen，et al.The research on the key factor affect the precision in stress analysis for the rotor of steam turbine［J］.Applied mechanics and materials，2013，275-277:83-86.

［12］張超，徐自力，劉石，等.采用熱固雙向耦合模型的轉子熱應力計算方法研究［J］.西安交通大學學報，2014，48（4）:68-72. ZHANG Chao，XU Zili，LIU Shi，et al.Steam turbine rotor thermal stress calculation with thermo-structural coupled model［J］.Journal of Xi'an Jiaotong university，2014，48 （4）:68-72.

［13］李朝陽，張艷春.燃機渦輪盤三維瞬態溫度及應力場計算分析［J］.動力工程，2006，26（2）:211-214，294. LI Chaoyang，ZHANG Yanchun.Calculation and analysis of the transient 3-dimensional temperature and stress field of a gas turbine＇s disk［J］.Journal of power engineering，2006，26（2）:211-214，294.

［14］RAO P D，SARKAR A，SASTRI V M K.Finite element analysis of the three-dimensional transient temperature field in steam turbine casings［J］.International journal of mechanical sciences，1993，35（7）:587-595.

［15］NAGPURE H G，HANDA C C，VANALKAR A V，et al. Analysis of stresses in turbine rotor using finite element method（FEM）-a past review［J］.International journal of engineering science and technology，2012，4（3）:1037-1042.

本文引用格式：

徐寧，王慶超，劉占生，等.基于熱彈耦合的渦輪轉子瞬態熱沖擊研究［J］.哈爾濱工程大學學報，2016，37（7）:936-942.

XU Ning，WANG Qingchao，LIU Zhansheng，et al.Transient thermal impact research on turbine rotors based on thermoelastic coupling［J］.Journal of Harbin Engineering University，2016，37（7）:936-942.

Transient thermal impact research on turbine rotors based on thermoelastic coupling

XU Ning1，2，WANG Qingchao1，LIU Zhansheng1，YANG Fan1
（1.School of Energy Science and Engineering，Harbin Institute of Technology，Harbin 150001，China；2.CSIC Harbin No.703 Research Institute，Harbin 150078，China）

Thermal stress is one of the most important parameters in turbine rotors undergoing transient thermal impact，and it directly influences the safety and life of turbine rotors.Based on thermoelastic coupling derivation and finite element simulation，we analyzed the two types of typical turbine rotor structures undergoing transient thermal impact and investigated the transient thermal stress，temperature distributions，and resulting rule changes of the rotor structure parameters.In addition，to better understand the asymmetric thermal impact phenomenon of the turbine rotor when in operation，we investigated the heat conduction of the turbine rotor while undergoing circumferential asymmetric thermal impact.The results show that transient thermal stress on the turbine rotor is greater than the steady state thermal stress，and the rotor is affected by the corner radius，disk thickness，and disk to shaft ratio.These results could be used as a reference in early design stage for estimating the thermal fatigue life of a turbine rotor.

transient thermal impact；turbine rotor；thermal stress；asymmetric thermal load；thermal fatigue life

10.11990/jheu.201502026

O321；TK471

A

1006-7043（2016）07-936-07

2015-02-15.網絡出版日期：2016-05-27.

國家高技術研究發展計劃項目（2008AA05A302）.

徐寧（1983-），男，工程師，博士研究生；王慶超（1950-），男，教授，博士生導師；劉占生（1962-），男，教授，博士生導師.

徐寧，E-mail:xuning0451@foxmail.com.

網絡出版地址：http：//www.cnki.net/kcms/detail/23.1390.u.20160527.1445.026.html