優化的GM(1,1)冪模型在港口吞吐量預測中的應用

黃躍華, 陳海山

(1.天津海運職業學院， 天津 300350;2.溫州海事局, 浙江 溫州 325002)

HUANG Yuehua1， CHEN Haishan2

優化的GM(1,1)冪模型在港口吞吐量預測中的應用

黃躍華1, 陳海山2

(1.天津海運職業學院， 天津 300350;2.溫州海事局, 浙江 溫州 325002)

為有效預測港口吞吐量，應用優化理論，通過非線性規劃的方法求解冪指數，建立優化冪指數的GM(1,1)冪模型。首次將該模型應用于港口吞吐量預測中，并以天津港港口吞吐量數據為例進行模擬和預測。結果表明：基于優化冪指數的港口吞吐量GM(1,1)冪模型不但可以解決傳統冪模型建模方法與模型檢驗脫節的問題，而且其模擬和預測的精度均優于傳統GM(1,1)冪模型。因此，可將該優化的冪模型應用于港口吞吐量預測中。

交通運輸經濟學;吞吐量;預測；灰色系統；GM(1,1)冪模型；指數優化

HUANGYuehua1，CHENHaishan2

Abstract: The GM (1,1) power model with exponents optimized with nonlinear programming is built and used for predicting the throughput of Tianjin port. The exponent optimized GM (1,1) power model is superior to traditional GM (1,1) power model in that the method for building the model can also test the model. In addition, it gives more accurate estimates.

Keywords: traffic transport economics; throughput; prediction; grey system; GM(1,1) power model; exponent optimization

港口吞吐量預測在確定港口發展規劃方向、未來投資規模和未來經營管理策略等方面有著重要的作用。通過對港口貨物吞吐量進行科學、合理的預測，港口當局不僅能依據所預測的數據作出正確的決策，而且能避免港口發展的規模大于市場需求造成的資源浪費。目前預測港口吞吐量的方法有很多，如指數平滑法[1-2]、線性回歸法[3-4]、系統動力學法[5]、組合模型法[6]和灰色模型法[7-8]等，其中指數平滑法、線性回歸法、系統動力學法和組合模型法的一個共同特點是需要大量的相關統計數據，而這些數據在實際工作中難以滿足建模要求，同時變量選取不當也會導致預測效果不理想。

灰色理論將系統作為一個灰色系統過程，運用部分已知的信息挖掘未知信息，因而可不用研究影響港口吞吐量的內部相關因素及其相互關系，把影響吞吐量的因素作為一定范圍內變化的與時間有關的灰色變量，挖掘數據自身有用的信息建立模型、揭示規律、作出預測。[9]

GM(1,1)冪模型是一種重要的非線性灰色模型，傳統的GM(1,1)和灰色Verhulst模型均為冪模型的特殊形式。優化GM(1,1)冪模型的突出優點在于：與實際應用數據最匹配的冪指數的數值可通過一定的方法被找到，且模型能較好地反映實際數據的非線性特征，具有較高的模擬和預測精度。[10]王正新等[11]以平均相對誤差最小化為目標，以參數之間的關系為約束條件，構建非線性優化模型，對傳統GM(1,1)冪模型進行優化，并以我國高中升學率的數據為例進行驗證，其模擬和預測精度均高于傳統模型。這里首次將優化GM(1,1)冪模型應用于天津港口吞吐總量的預測中，實踐證明,改進的預測模型的預測精度相比傳統GM(1,1)模型[10]提高效果明顯，對促進港口正確決策具有重大意義。

1 傳統GM(1,1)冪模型

GM(1,1)冪模型的計算方法如下。

1.1模型建立

1)設港口歷史吞吐量數據為

X(0)=(x(0)(1),x(0)(2),…,x(0)(n))

(1)

2)對吞吐量數據進行一階累加,得

X(1)=(x(1)(1),x(1)(2),…,x(1)(n))

(2)

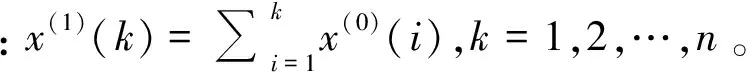
3)根據X(1)序列生成緊鄰均值序列,即

Z(1)=(z(1)(1),z(1)(2),…,z(1)(n))

(3)

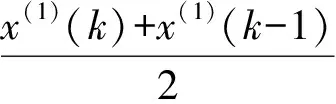
4)設x(0)(k),x(1)(k),z(1)(k)如上所述，則灰色微分方程為

x(0)(k)+az(1)(k)=b(z(1)(k))α,α≠1

(4)

該方程稱為GM(1,1)冪模型。

5)GM(1,1)冪模型白化微分方程為

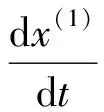
(5)

式(5)中:a,b,α為待定系數；t為時間。

1.2模型參數求解

根據式(4)對參數列(a,b)T作最小二乘估計,得

(a,b)T=(BTB)-1BTY

(6)

式(6)中：

求解式(5)便可得時間響應式為

(7)

(8)

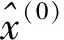
2 GM(1,1)冪模型的冪指數優化[11]

GM(1,1)冪模型冪指數優化計算方法如下。

由式(6)可知，若冪指數α確定，則公式模型中參數a和b也就隨之確定。首先展開GM(1,1)冪模型中的參數a和b的表達式，并將數據矩陣B和Y代入到式(6)中整理得

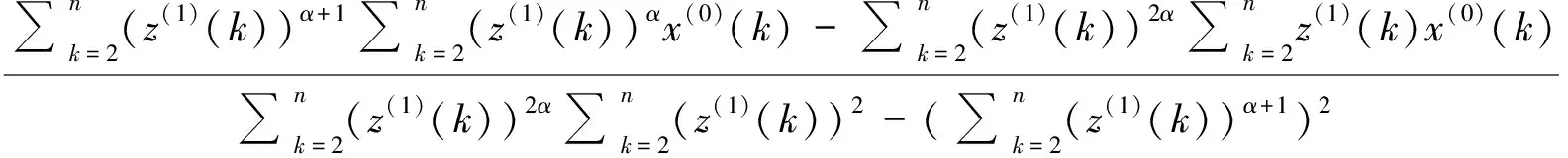
(9)

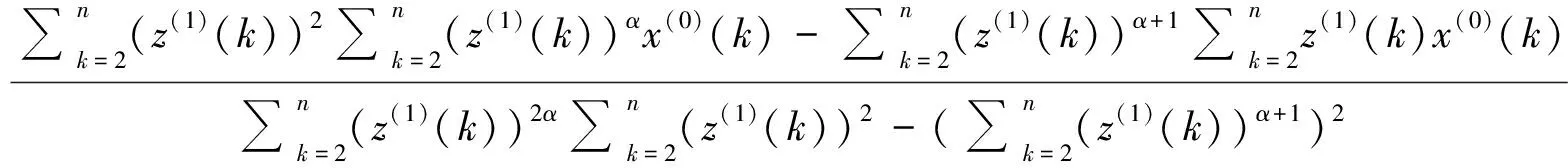
(10)

以獲得的預測吞吐量平均相對誤差最小化為目標，以冪指數α與參數a和b之間的關系為約束條件建立下列優化模型，求得最優的冪指數α的值，使吞吐量預測模型的平均相對誤差的絕對值在理論上達到最小。

(11)

(12)

運用MATLAB和Excel等相關軟件，根據式(11)和式(12)可很方便地求解式(7)中的參數α,a和b的優化值。將通過以上方式獲得的參數值代入到式(7)中便可獲得優化模型。

3 模型精度評估

3.1殘差的相對誤差檢驗

殘差為實際吞吐量與預測吞吐量之間的差，將第k時刻的吞吐量相對誤差(Throughput Relative Percentage Error)記為TRPE(k)，其表達式為

(13)

將所有時刻的吞吐量平均相對誤差(Throughput Average Relative Percentage Error)記為TARPE，其表達式為

(14)

1)當k≤n時，稱TRPE(k)為k時刻吞吐量模擬相對誤差;當k>n時，稱TRPE(k)為k時刻吞吐量預測相對誤差，稱TARPE為吞吐量平均模擬相對誤差;當TRPE和TARPE在要求的相對誤差范圍內時，稱吞吐量模型為殘差合格模型。

2)吞吐量平均模擬相對精度為1-TARPE(k);1-TRPE為k時刻吞吐量模擬相對精度。

3.2模型精度檢驗標準[10]

通常將誤差5%設定為界定標準，即當殘差的相對誤差<5%時為殘差合格模型，相對誤差>5%時認為殘差不合格。

4 模型驗證評價及預測

為評價優化冪模型的模擬和預測效果，選用天津港2006—2014年的吞吐量數據(見表1)對模型進行模擬和預測效果驗證,數據來自于天津市統計局網站。選取天津港2006—2012年的吞吐量數據作為建模數據，2013—2014年的數據作為驗證數據。

表1 2006—2014年天津港貨物吞吐量數據 萬t

4.1傳統冪模型求解方法[10]

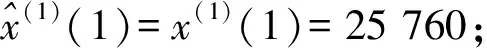
4.2優化冪指數計算方法

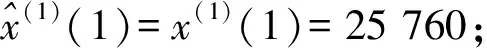
根據式(8)、式(13)和式(14)對吞吐量預測值再作一階累減還原計算，并預測2013—2014年的吞吐量。2種模型的模擬和預測精度比較見表2。

由表2可知，建立的吞吐量優化模型的模擬精度顯著高于傳統模型，優化模型完全滿足TARPE<5%和TRPE<5%的要求，為殘差合格吞吐量預測模型。與傳統模型相比，優化模型在預測方面的優勢也十分明顯，同時1步預測、2步預測的相對誤差均在2%之內。

4.3利用優化模型進行預測

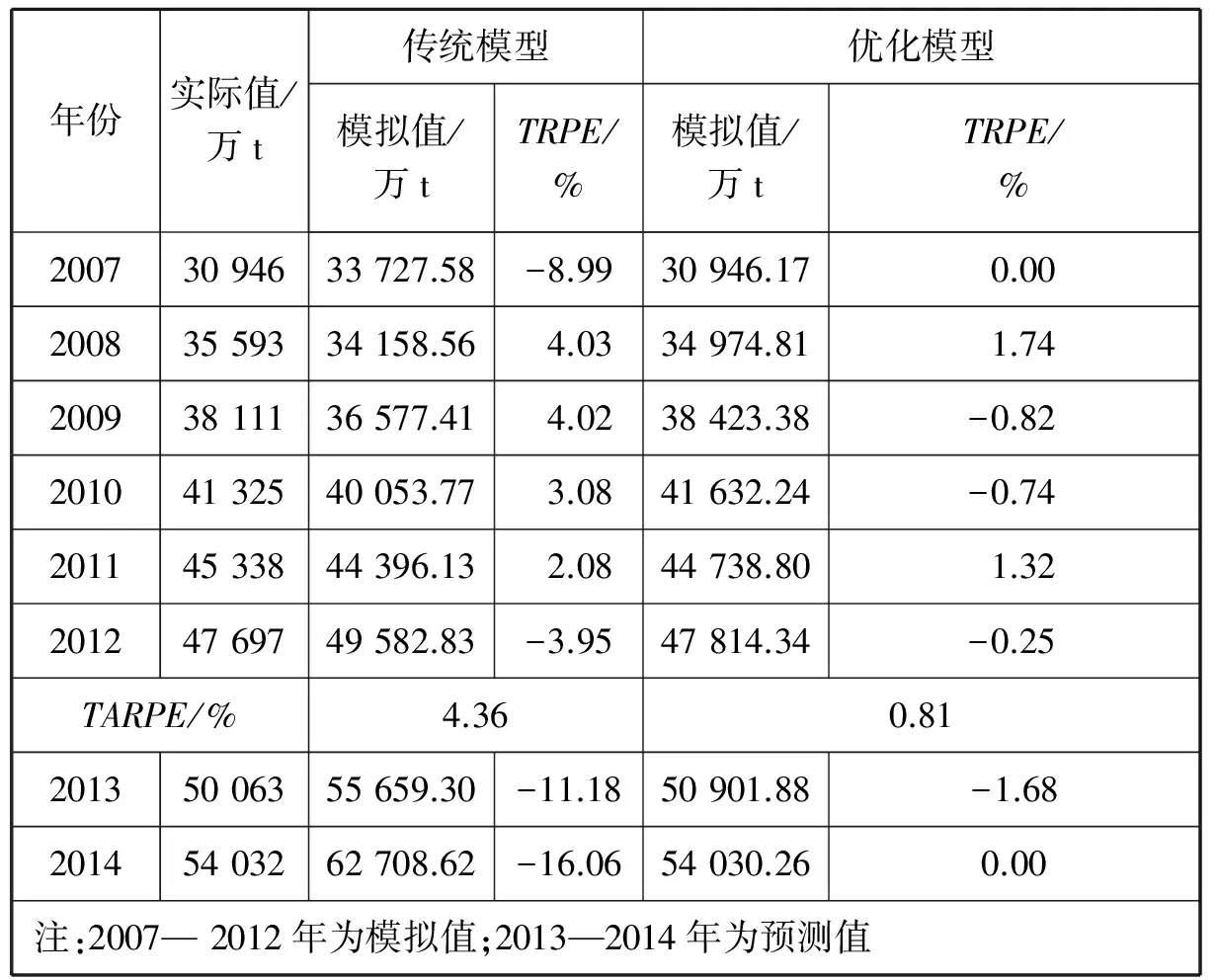
表2 2007—2014年天津港貨物吞吐量2種模型的數據比較

根據式(8)、式(13)和式(14)對吞吐量預測值再作一階累減還原計算，并預測2015—2017年吞吐量，模型的模擬與預測精度比較見表3。

表3 2015—2017年天津港貨物吞吐量預測

由表3可知，TARPE=0.66<5%且TRPE<5%，模型為殘差合格吞吐量預測模型，預測2015—2017年吞吐量分別為56 840.25萬t,60 064.61萬t和63 401.62萬t。

5 結束語

應用冪模型優化理論,通過非線性規劃的方法優化冪指數，找到最佳擬合吞吐量數據的模型，為提高吞吐量數據建模精度提供一種有效的途徑。結果表明，該模型與傳統GM(1,1)冪模型相比可顯著提高模擬和預測精度。此外,通過預測天津港2015—2017吞吐量為港口規劃發展提供參考。

[1] 關克平,齊夢雅.基于指數平滑法的寧波-舟山港港口吞吐量預測研究[J]. 中國水運(下半月),2013(12):28-29.

[2] 王慧,陳浩.基于三次指數平滑法的欽州港貨物吞吐量預測[J].珠江水運, 2013(Z1):169-170.

[3] 王文.線性回歸結合季節性復合序列的深圳港集裝箱吞吐量預測[J].中國水運(下半月),2012(12):23-25.

[4] 陳秀瑛,古浩.灰色線性回歸模型在港口吞吐量預測中的應用[J]. 水運工程,2010(5):90-92.

[5] 許長新,嚴以新,張萍.基于系統動力學的港口吞吐量預測模型[J].水運工程, 2006(5):26-28.

[6] 趙剛,朱超,封學軍.組合預測在港口吞吐量預測中的應用研究[J].水運工程,2005(3):34-36.

[7] 陳潔,許長新.改進的灰色模型在港口吞吐量預測中的應用[J]. 水運工程, 2005(1):20-23.

[8] 林強,陳一梅.灰色多元回歸模型在港口吞吐量預測中的應用[J].水運工程, 2008(7):77-80.

[9] 王正新,黨耀國,劉思峰,等.GM(1,1)冪模型求解方法及其解的性質[J].系統工程與電子技術, 2009, 31(10): 2380-2383.

[10] 鄧聚龍.灰色預測與決策[M].武漢:華中理工大學出版社，2002:176-177.

[11] 王正新,黨耀國,趙潔玨.優化的GM(1,1)冪模型及其應用[J].系統工程理論與實踐,2012,32(9):1973-1976.

OptimizedGM(1,1)PowerModelforPredictingPortThroughput

(1. Tianjin Maritime College, Tianjin 300350, China；2. Wenzhou MSA, Wenzhou 325002, China)

U691.71

A

2016-01-30

黃躍華(1980—)，男，天津人，講師，碩士，從事舶舶交通工程研究。E-mail:11618378@qq.com

1000-4653(2016)02-0131-04