空化器參數對超空泡初生位置影響大渦模擬

張　木,譚俊杰,易文俊,廖選平

(1.中國運載火箭技術研究院 戰術武器事業部,北京 100076;2.南京理工大學 能源與動力工程學院,南京 210094;3.南京理工大學 瞬態物理國家重點實驗室,南京 210094)

?

空化器參數對超空泡初生位置影響大渦模擬

張木1,譚俊杰2,易文俊3,廖選平1

(1.中國運載火箭技術研究院 戰術武器事業部,北京 100076;2.南京理工大學 能源與動力工程學院,南京 210094;3.南京理工大學 瞬態物理國家重點實驗室,南京 210094)

為揭示空化器參數對超空泡初生位置的影響規律,離散求解了三維氣液兩相大渦模擬控制方程組,對三維不同空化器參數模型下超空泡流動進行了數值模擬。在不同空化數條件下,通過數值模擬獲得超空泡無量綱幾何參數并與實驗數據對比,結果表明兩者吻合良好。在此基礎上,分析了不同空化器形狀、直徑對超空泡初生位置影響。分析結果為探索高速航行體空化器性能與水動力特性提供了數值參考。

超空化;大渦模擬;超空泡初生位置;氣液兩相流動;數值模擬

俄羅斯高速超空泡魚雷的出現，促使超空泡武器吸引了世界各大軍事強國的關注,并紛紛投入大量科研力量開展空化現象的研究。空化流動是一種考慮相變、粘性、湍流運動、界面可壓縮性的極其復雜的多相流動現象。早期由于受到多相流理論及計算機硬件設備等條件的制約,研究人員主要利用勢流理論方法[1],其中具有代表性的研究有:Helmholtz[2]基于勢流理論,分析了繞二維平板的超空泡流動現象;Riabouchinsky[3]提出了有限長度空泡模型。隨著多相流理論和計算機硬件設備條件取得長足進展,研究人員開始廣泛使用離散求解N-S方程的算法進行機理研究與工程應用[1]。例如:Delannoy和Kueny假設流動狀態為等溫且不考慮氣相與液相的可壓縮性,研究了不同模型下的空化流動問題[4-5]。Hesister依托Delannoy的研究結果,優化了混合密度求解方程,引入壓力的影響[6]。黃海龍等[7]針對三維圓盤空化器模型,分析了變攻角條件下超空泡流動。周景軍、于開平研究了低弗勞德數下通氣超空泡泄氣機理,揭示了弗勞德數與通氣率對空泡泄氣的影響規律[8-9]。綜合上述分析可知,目前超空泡研究主要集中在大空化數(空化數小于0.01)，采用雷諾平均湍流模型方法。結合國內外相關研究情況,本文研究了小空化數下空化器參數對超空泡初生位置的影響。

1　控制方程

1.1大渦模擬

本文基于VOF方法、大渦模擬湍流模型,以及空化模型,對超空化流動進行數值仿真,其濾波后的控制方程可寫為

(1)

(2)

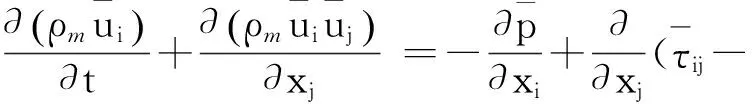
(3)

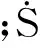
(4)

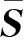
(5)

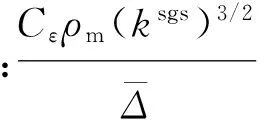
1.2空化模型

為模擬氣相與液相間的相變質量傳遞過程,本文采用Kunz空化模型,其表達式為

(6)

(7)

式中:Cprod,Cdest為模型系數;t∞=L/v∞,L為計算域長度;v∞,ρv,ρl分別為來流速度、氣相與液相密度;其他變量參數詳見文獻[10]。

2　離散方法

本文計算中N-S方程組的對流項、擴散項以及時間項離散方法詳見文獻[1]。為實現氣液交界面的可壓縮性計算,引入基于PISO算法的密度-壓力-速度耦合算法[10]。

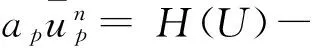
(8)

式中:ap為單元中心項系數,H(U)表示相鄰節點項以及源項之和,ΔVp為單元體積。將預估壓力分布p*代入式(8)求解出近似速度分布u*,v*,w*。

查看u*,v*,w*在連續性方程中的適應性,若適應性不符合連續性方程條件需進行第1次修正,即求解如下方程:

·(U*)p-

(9)

式中：ΔVp為計算單元體積。式(9)考慮了氣液兩相界面可壓縮性影響。通過式(9)求解出經過第一次校正步后的速度、壓力改進值U**和p**。

第2壓力修正方程為

·(U**)p+

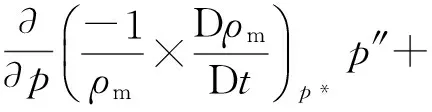
(10)

將U**,p**代入式(10)所示的第2壓力修正方程,求解出流場的速度與壓力值。

3　計算結果與分析

3.1計算結果與試驗結果對比

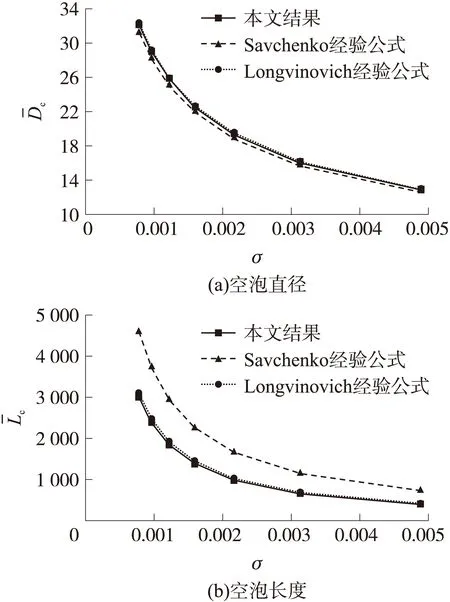
圖1　超空泡幾何參數隨空化數變化

由圖1可知,隨著空化數增加,空泡長度、直徑均降低。本文空泡直徑計算結果與經過試驗驗證的Longvinovich[11]經驗公式和Savchenko[12]經驗公式吻合良好。本文空泡長度計算結果與Longvinovich經驗公式吻合良好,這是由于Longvinovich經驗公式適用空化數范圍為0～2.5×10-1,而Savchenko經驗公式適用空化數范圍為1.2×10-3～5.7×10-3。數值模擬結果與試驗結果變化趨勢基本一致且吻合良好。

3.2不同空化器直徑對超空泡初生位置的影響

在FVM(finite volume method)方法計算中,為提高計算效率和精度,本文采用分塊結構化網格方法實現三維圓盤空化器航行體模型(長徑比為10)網格劃分,如圖2所示。

本文計算對象的航行速度小于水下聲速,為保證航行體表面的流動不會受到遠場的影響,并且考慮到超空泡長度的影響,本文選取如圖3所示的計算域范圍。除計算域右端為壓力出口邊界條件外,其余均為速度入口邊界條件,航行體表面為固壁邊界條件,速度為無滑移邊界條件。

在空化器直徑分別為Dn=5 mm,3.5 mm,2 mm;攻角α=0°,空化數σ=2.17×10-3條件下,對圓盤空化器航行體超空泡流動現象進行了計算,分析了空化器直徑對超空泡初生位置的影響。計算結果如圖4所示,圖中,φl表示液相體積分數。

圖2　計算網格

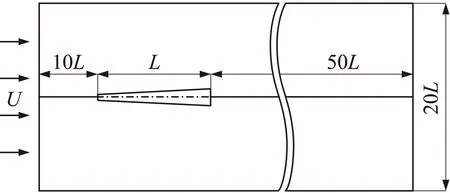
圖3　計算域示意圖

圖4、圖5分別為不同空化器直徑下空泡等值面圖和液相體積分數圖。由圖4、圖5可知,當Dn=2 mm時,航行體表面無法被空泡整體覆蓋,頭部空化器和航行體表面部分區域外露,處于粘濕狀態,頭部超空泡初生位置距離空化器頂點明顯靠后,尾部超空泡初生位置出現在錐-柱連接處,這樣會導致航行體受力特性發生變化,對航行體運動穩定性和水動力特性存在較大影響。當3.5 mm≤Dn≤5 mm時,航行體表面完全被空泡整體覆蓋,超空泡初生位置出現在空化器頂端,且航行體表面空泡厚度隨空化器直徑增加而增厚,空泡空化效果越好。航行體上表面空泡厚度隨空化器直徑的變化曲線如圖6所示，圖中，X/L表示航行體無量綱軸向位置,h表示上表面空泡厚度。

圖4　不同空化器直徑下空泡等值面圖

圖5　不同空化器直徑下液相體積分數圖

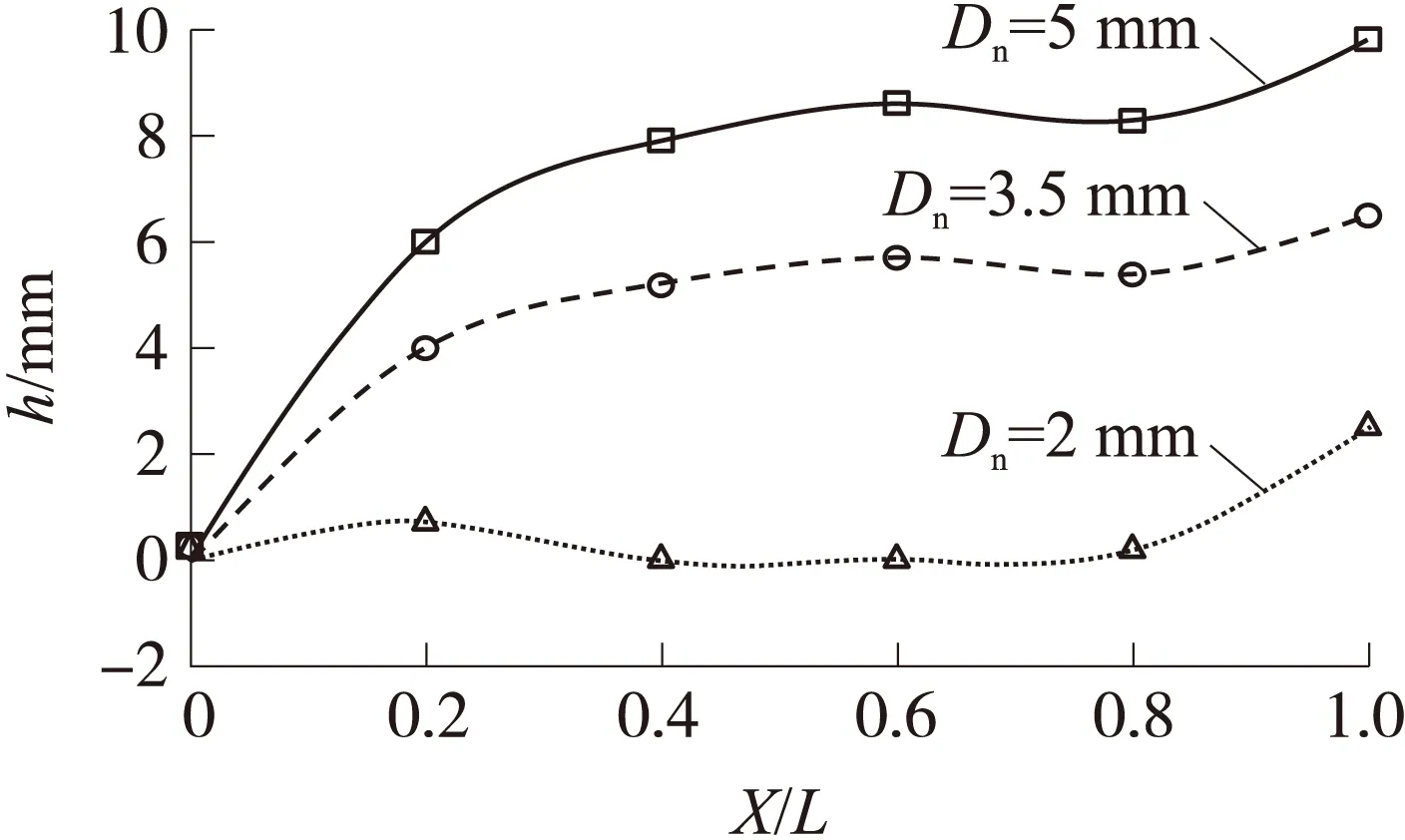
圖6　航行體上表面空泡厚度隨空化器直徑變化曲線

由圖6可知,從航行體頭部前緣起,當Dn=2 mm,0≤X/L≤0.6時,空化器直徑小導致航行體表面無法被空泡整體覆蓋,因此上表面空泡先增大再減小到0;當Dn=2 mm,0.6

柱連接處形成低于臨界空化壓力區,再次產生尾端空泡,因此上表面空泡最后逐漸增大。從航行體頭部前緣起,當3.5 mm≤Dn≤5 mm,0≤X/L≤1時,由于航行體表面完全被空泡整體覆蓋,因此在空化器直徑不變條件下, 上表面空泡整體呈增大趨勢。

在無量綱軸向位置相同情況下,當2 mm≤Dn≤5 mm時,上表面空泡隨空化器直徑增加而變厚。

3.3不同空化器形狀對超空泡初生位置的影響

在α=0°,σ=2.17×10-3,Dn=5 mm條件下,計算了3種典型空化器頭型航行體超空泡流動,結果如圖7所示; 小空化數條件下不同空化器形狀對空泡初生位置的影響規律如圖8、圖9所示。

圖7　超空泡幾何參數隨空化數變化

圖8　不同空化器形狀下航行體液相體積分數云圖

圖9　不同空化器形狀下航行體頭部空泡等值面圖

由圖可知,圓盤空化器模型頭部超空泡初生位置距離空化器頂端0 mm,1/4球形空化器模型頭部超空泡初生位置距離空化器頂端2.46 mm,而150°錐角圓錐空化器模型頭部超空泡初生位置位于兩者之間,其距離空化器頂端1.05 mm。由此可得出,在空化數、空化器直徑以及攻角一定的條件下,圓盤空化器航行體的粘濕面積最小,1/4球形空化器航行體的粘濕面積最大。此外,為保持超空泡航行體的運動穩定性,應盡可能減小航行體的粘濕面積。綜合上述分析可知,在空化數、空化器直徑以及攻角一定的條件下,圓盤空化器的超空泡初生位置出現在空化器頂端,具有良好的超空泡生成能力。

4　結論

本文離散求解三維氣液兩相大渦模擬控制方程組,探究了繞三維不同空化器參數航行體模型的超空泡流動現象,揭示了小空化數下不同空化器參數對超空泡初生位置的影響并獲得如下相關結論:

①通過數值模擬獲得了無量綱空泡幾何參數隨空化數的變化規律,并且本文數值模擬結果與Logvinovich、Savchenko試驗結果吻合良好。

②揭示了超空泡初生位置隨空化器直徑的變化規律,分析結果顯示,當Dn=2 mm時,航行體表面無法被空泡整體覆蓋,頭部超空泡初生位置距離空化器頂端明顯靠后,尾部超空泡初生位置出現在錐柱連接處,導致航行體受力特性發生變化,影響運動穩定性;當3.5 mm≤Dn≤5 mm時,航行體表面完全被空泡整體覆蓋,超空泡初生位置位于空化器頂端。

③探究了不同空化器形狀對超空泡初生位置的影響,分析結果表明,在空化數、空化器直徑以及攻角一定的條件下,圓盤空化器模型的超空泡初生位置出現在空化器頂端,具有良好的超空泡生成能力。

[1]張木,易文俊,譚俊杰,等.帶尾翼水下自然超空泡射彈數值模擬研究[J].計算力學學報,2013,30(1):161-165.

ZHANGMu,YIWen-jun,TANJun-jie,etal.Numericalinvestigationofunderwaternaturalsupercavitatingprojectilesoperatingwiththeempennages[J].ChineseJournalofComputationalMechanics,2013,30(1):161-165(inChinese)

[2]NOURINM,ESLAMDOOSTA.Aniterativeschemefortwo-dimensionalsupercavitatingflow[J].OceanEngineering,2009,36(9):708-715.

[3]RIABOUCHINSKYD.Onsteadyfluidmotionwithfreesurfaces[J].ProceedingsoftheLondonMathematicalSociety,1921,19(1):206-215.

[4]DESHPANDEM,FENGJ,MERKLECL.CavityflowpredictionsbasedontheEulerequations[J].JournalofFluidsEngineering,1994,116(1):36-44.

[5]KARIMMM,AHMMEDMS.NumericalstudyofperiodiccavitatingflowaroundNACA0012hydrofoil[J].OceanEngineering,2012,55(15):81-87.

[6]CHENY,HEISTERSD.Modelinghydrodynamicnonequilibriumincavitatingflows[J].JournalofFluidsEngineering,1996,118(1):172-178.

[7]黃海龍,魏英杰,黃文虎,等.重力場對通氣超空泡影響的數值模擬研究[J].哈爾濱工業大學學報,2007,39(5):800-803.

HUANGHai-longWEIYing-jie,HUANGWen-hu,etal.Numericalsimulationstudyoftheinfluenceofgravityfieldontheventilatedsupercavity[J].JournalofHarbinInstituteofTechology,2007,39(5):800-803.(inChinese)

[8]周景軍,于開平,楊明.低弗魯德數條件下通氣超空泡泄氣機理數值模擬[J].工程力學,2011,28(1):251-256.

ZHOUJing-jun,YUKai-ping,YANGMing.NumericalsimulationofgasleakagemechanismofventilatedsupercavityundertheconditionoflowFroudenumber[J].EngineeringMechanics,2011,28(1):251-256.(inChinese)

[9]YUKai-ping,ZHOUJing-jun,MINJing-xin,etal.AcontributiontostudyontheliftofventilatedsupercavitatingvehiclewithlowFroudenumber[J].JournalofFluidsEngineering,2010,132(11):1-7.

[10]張木,譚俊杰,易文俊,等.非定常水下超空泡射彈大渦模擬研究[J].彈道學報,2012,24(3):91-95.ZHANGMu,TANJun-jie,YIWen-jun,etal.Largeeddysimulationofthree-dimensionunsteadyflowoverunderwatersupercavitatingprojectile[J].JournalofBallistics,2012,24(3):91-95.(inChinese)

[11]SEVCHENKOYN,SEMENENKOVN,SEREBRYAKOVVV.Experimentalstudyofthesupercavitationflowsatsubsonicflowvelocities[J].DokladyANUkrainy,1992,42(2):64-69.

[12]SEVCHENKOYN.Experimentalstudyofhigh-speedcavitationflow[J].Hydromechanics,1998,72(1):103-111.

LargeEddySimulationAnalysisonEffectofCavitatorParameteronSupercavityPrimaryPosition

ZHANGMu1,TANJun-jie2,YIWen-jun3,LIAOXuan-ping1

(1.PWD,ChinaAcademyofLaunchVehicleTechnology,Beijing100076,China;2.SchoolofEnergyandPowerEngineering,NanjingUniversityofScienceandTechnology,Nanjing210094,China;3.StateKeyLaboratoryofTransientPhysics,NanjingUniversityofScienceandTechnology,Nanjing210094,China)

Inordertorevealtheeffectofcavitatorparameterontheprimarypositionofsupercavity,thethree-dimensiongas-liquidLES(largeeddysimulation)Navier-Stokesequationswerediscretedandsolved.Thenumericalsimulationofthree-dimensionsupercavitatingphenomenonflowaroundnavigationbodieswithdifferentcavitator-parameterswerecarriedout.Thedimensionlessgeometricparametersofsupercavityundertheconditionsofdifferentcavitationnumberswereobtained.Thecalculationresultwascomparedwithexperimentalresult.Thenumericalresultagreeswellwiththeexperimentalresult.Onthisbasis,thesupercavitatingflowsaroundnavigationbodywhichhasbeencalculatedatdifferentcavitatordiametersandcavitator-shapes.Theeffectsofdifferentcavitator-shapesanddiametersonsupercavitypromarypositionwereanalyzed.Theanalysisresultoffersacademicreferenceforthestudyofhydrodynamicsandcavitatorperformanceofhigh-speedbodies.

supercavitation;largeeddysimulation;supercavityprimaryposition;gas-liquidflow;numericalsimulation

2015-04-08

張木(1985- ),男,工程師,博士,研究方向為多相流場數值模擬。E-mail:nanjingzhangmo@163.com。

O351.3

A

1004-499X(2016)01-0087-05