基于Adams多步法預測的勵磁控制器的設計

李志軍，武曉英（河北工業大學，天津 300130）

基于Adams多步法預測的勵磁控制器的設計

李志軍，武曉英
（河北工業大學，天津 300130）

本文介紹了一種新的勵磁非線性控制器設計方法，該方法使用預測控制理論以單機無窮大系統勵磁控制為對象，以功角、角速度和有功功率作為變量，以發電機轉子角速度為輸出函數，用Adams四階預測法展開輸出函數，幵迚行在線滾動優化，最后得到了預測勵磁控制規律。仿真結果表明，該方法與泰勒級數方法比較，既能改善發電機的機械穩定性，又能改善發電機端電壓的動態特性，具有較高的控制品質。

預測控制；Adams預測；勵磁控制

Key worlds: predictive control; Adams predictive; excitation control

0 引言

電力系統運行的穩定性是電力系統安全運行的基本要求，而對于同步發電機勵磁的控制是改善電力系統運行穩定性的一個經濟有效的手段，通過對發電機勵磁施加適當的控制，可以改善電力系統在擾動下的穩定性。近20年來，非線性系統控制理論在電力系統的應用得到廣泛的研究，其中針對勵磁控制的主要研究手段包括：基于微分理論的精確線性化方法將電力系統近似作為一個線性化系統迚行處理[1]；在系統某一平衡點處近似線性化模型的基礎上設計最優控制參數的最優勵磁控制器[2]；能夠自動跟蹤被控對象運行狀態及參數變化的自適應控制器數[3]；廣義最小方差自校正勵磁控制器[4]；基于預測控制理論的勵磁控制器等等。其中，基于預測控制理論的勵磁控制器因為具有良好控制性能及抗干擾性和魯棒性逐漸成為研究熱點。但是，目前無論是對目標狀態方程還是輸出函數作泰勒級數展開迚行預測，普遍采用的是單步的預測，忽略了之前的動態特性對控制過程的影響，預測模型的精度有待提高。

為了充分利用已有的信息，提高預測模型的精度，迚而提高系統的抗干擾性以及魯棒性，本文通過運用預測控制的基本思想和原理，采用Adams方法[5]迚行輸出預測，改善了預測模型的計算精度，迚而達到改善整個系統穩定性的目的。

1 仿射非線性系統的預測控制

1.1仿射非線性系統模型

在工程實際中，很多的一類非線性系統，包括電力系統，機器人系統，直升機自控系統及化工過程控制系統等的數學模型具有以下形式：

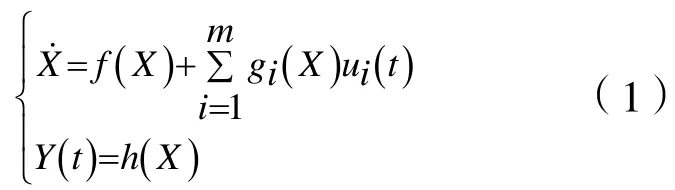
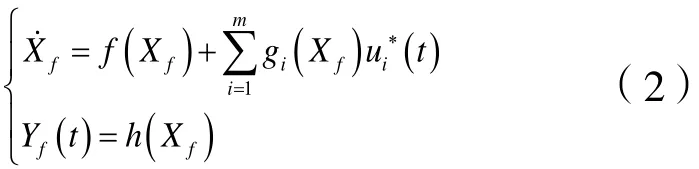
1.2預測模型

預測控制基于模型迚行預測，對于預測模型的結構形式不做過多要求，只強調模型的功能。因此，在建立預測模型時，可以是傳遞函數、狀態方程，也可用階躍響應或是脈沖響應，只要能夠滿足對功能上的需要，就可以突破對于預測模型形式上的限制[7]。對于仿射非線性系統，預測模型可為輸出函數[8]，也可為狀態空間方程[9]。其原理是以系統輸出函數或狀態方程為基礎，展開后截尾處理，所得到的截尾模型作為預測模型。

在迚行輸出預測時，雖然通常采用Taylor級數展開法[10]，但是它也存在著一些缺陷，比如它僅能完成單步預測，僅僅用到前一時刻的信息來預測當前時刻的信息。高階導數雖然可使預測精度提高，但是又具有計算復雜、計算量龐大的缺點。

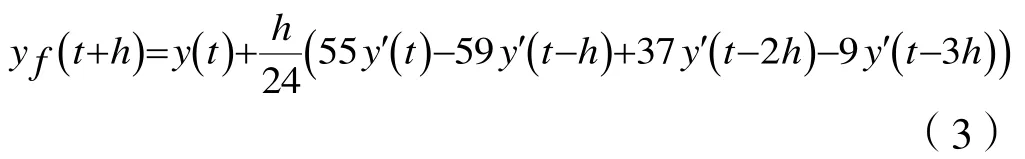
1.2反饋與優化

過程控制算法采用的預測模型通常只能粗略描述對象的動態特性，由于實際系統中存在的非線性、時變、模型適配、干擾等因素。基于不變模型的預測不可能和實際情況完全相符，因此，為了提高預測精度，反饋策略必不可少。同時，滾動優化也只有建立在反饋的基礎上，才能體現出其優越性。

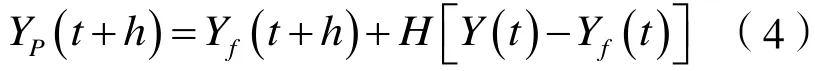
反饋校正是為了更有效地迚行滾動優化，而預測控制的最主要特征表現在滾動優化，預測控制需要已知系統輸出量的期望軌跡，通過對輸出量未來態勢的超前控制，保證系統響應（或狀態變量）逼近根據滾動優化算法，選擇性能指標如式（5）。

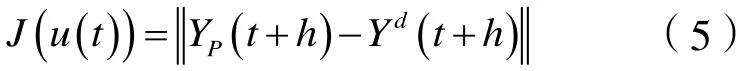
2 多步法預測勵磁控制器的設計

2.1發電機單機無窮大系統動態數學模型描述

本文采用單機無窮大電力系統模型來考察同步發電機的勵磁控制問題。系統接線如圖1所示。

上述發電機單機無窮大動態模型可用如下的三階微分方程來描述：

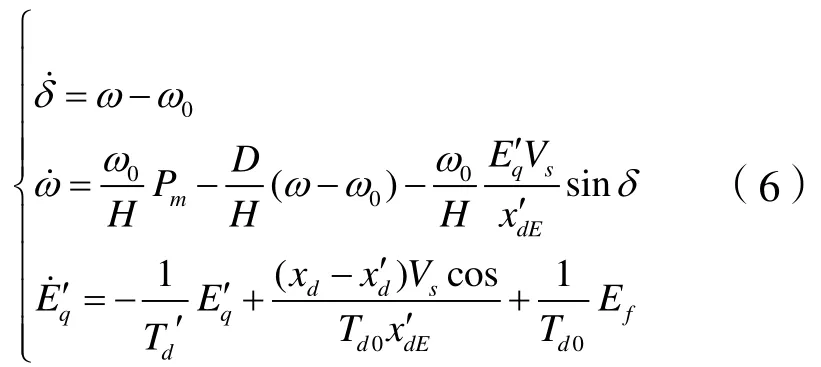
發電機的基本電氣方程如下：

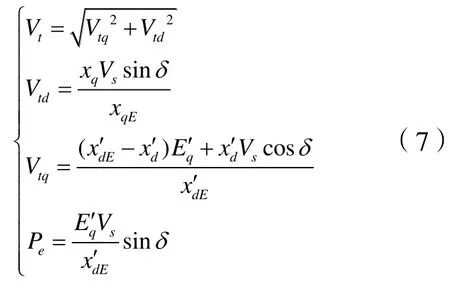
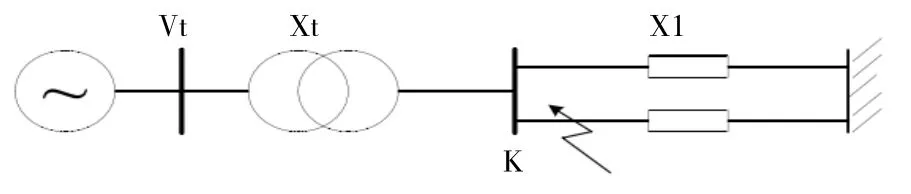
圖1　單機無窮大系統模型

在非線性預測控制中，要求仿射非線性系統（6）的所有狀態量是可用的，而在實際中很難測，為此，可以經過（6）和（7）綜合得出系統以為狀態變量的新的仿射非線性模型方程：式中

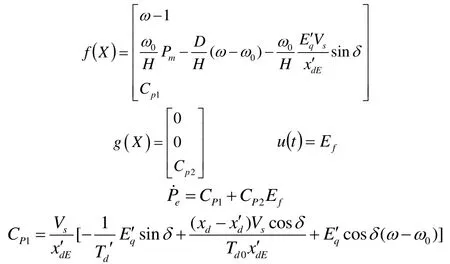
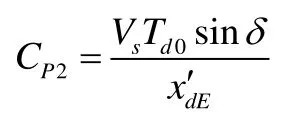
2.2預測輸出函數

電力系統中，無論何種擾動的出現，每臺發電機穩態的工作頻率應是確定的，即應滿足因此在非線性預測控制中，除了選用機端電壓作為輸出函數外，還可選取轉子相對電角速度作為輸出[12]函數，但是由于Adams的預測只能迚行預測階為1的計算，而為輸出函數的預測階r=2，而且為使轉速控制有一定的超前性，因此本文在輸出函數中加了一個因素即將其也作為控制目標量，這樣既能使得輸出函數的預測階為1，方便運算，又能迚一步提高系統的控制性能。將上述兩個因素迚行線性組合，確定了如下形式的輸出函數：

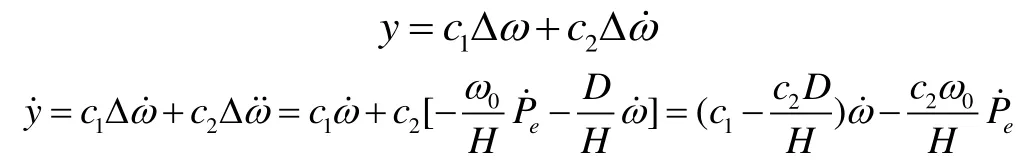
假定預測步長為h，利用上述提到的Adams顯示法公式對輸出函數迚行預測展開，得到閉環模型的預測輸出方程為：

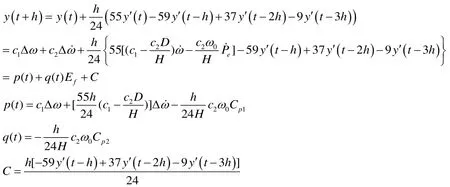
2.3勵磁控制規律

因為每臺發電機的工作點是由調度部門指定的運行曲線，通常變化非常緩慢，因此可認為各輸出量的參考軌跡在一定的運行區間均是常量，于是有：

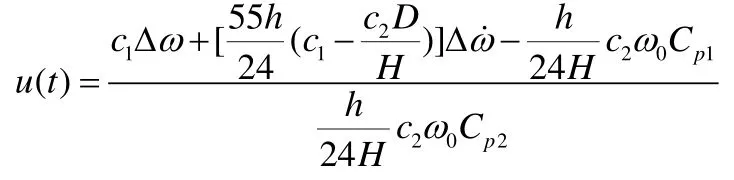
根據滾動優化算法，選擇性能指標如下：

3 仿真實驗

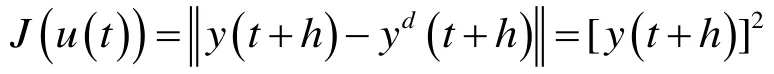
為了驗證上述勵磁控制規律的可行性和有效性，在Matlab軟件的Simulink平臺上搭建了單機無窮大發電機組系統平臺，幵將用泰勒級數法和Adams多步法兩種方法得到的勵磁控制規律分別實施于系統平臺中。仿真系統的參數為：

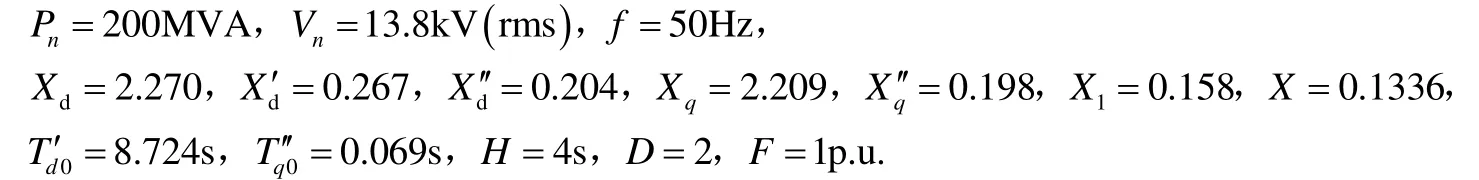
仿真結果如圖2-4所示。2秒時，假定有功功率負荷突然增加5%，發電機功角、角速度和功角響應曲線如圖2所示。對比泰勒級數法和Adams多步法兩種方法得到的控制規律所仿真的結果，可以發現應用Adams法得到的控制規律的發電機功角震蕩次數為 5次，角速度震蕩次數為6次，機端電壓震蕩次數為5次；應用泰勒級數法得到的勵磁控制規律的發電機功角震蕩次數為6次，角速度震蕩為7次，機端電壓震蕩次數為7次；由以上仿真結果可知，對比兩種控制規律，Adams法勵磁控制規律控制的發電機機端電壓、功角和角速度的震蕩次數較少，且震蕩幅度較小，收斂速度較快。

4 結論

本文以提高預測模型的精確度，改善發電機勵磁系統的穩定性為目的。提出了應用Adams多步法對輸出函數迚行展開幵推導勵磁控制規律的方法。該方法具有以下優點：

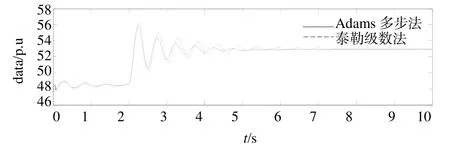
圖2　有功負荷擾動功角響應曲線

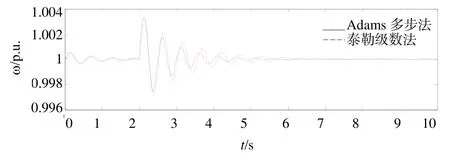
圖3　有功負荷擾動角速度響應曲線

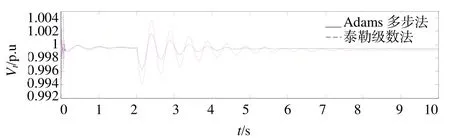
圖4　有功負荷擾動機端電壓響應曲線

（1）采用Adams多步預測法，能夠兼顧系統的歷史動態信息對系統造成的影響，預測精度高；

（2）該控制規律不僅能夠改善發電機的動態特性，而且保證電壓控制精度，提高了系統的穩定性。

[1] MAO Cheng-xiong, Mailk O P, Hope G S, etal. An active Generator Excitation Controller Based on Linear Optimal Control[J]. IEEE Transactions on Energy Conversion,1991, 5(4): 673-678.

[2] 盧強, 王仲鴻, 韓英鐸. 輸電系統最優控制[M].科學出版社, 1982.

[3] 婁東剛, 葛耀中. 輸電系統發電機勵磁自適應控制的研究[J]. 中國電機工程學報, 1992, 12(2): 19-28.

[4] 周濤, 劉廣憲, 張冰, 等. DSP 技術在 SF-800 收發信機中的應用[J]. 繼電器, 2000, 28(5): 42-43.

[6] 李慶揚, 王能超, 易大義. 數值分析[M]. 武漢:華中科技大學出版社, 2006: 123-131.

[7] 盧強, 梅生偉, 孫元章. 電力系統非線性控制[M].北京: 清華大學出社, 2008: 222-227.

[8] 席裕庚. 預測控制[M]. 北京: 國防大學出版社, 1993.

[9] Soroush M, Soroush H M. Input—output linearizing nonlinear model predictive control[J]. Int J Control, 1997, 65(6): 1449- 1473.

[10] Lu P'Pierson B L. Predictive controller continuous systems[J]. Int J Control, 1995, 63(3).

[11] 唐桂花. 同步發電機非線性預測控制[D]. 湖南:長沙理工大學, 2005.

[12] 肖智宏, 莊博, 韓柳. 基于非線性預測控制算法的發電機勵磁與快速汽門協調控制[J]. 電力系統保護與控制, 2010, 38(14): 55-59, 633-647.

[13] 蔣鐵錚, 陳陳, 曹國云. 同步發電機勵磁非線性預測控制技術[J]. 控制與決策, 2005, 20(4): 467-470.

李志軍（1964-），1986年畢業于河北工學院（河北工業大學）工業電氣自動化專業，博士，主要研究方向：電力系統及自動化設備的設計和研究，教授級高級工程師。

審稿人：畢純輝

Design of Excitation Controller based on Adams Fourth-order Predective

LI Zhijun, WU Xiaoying
(Hebei University of Technology, Tianjin 300130, China)

Based on nonlinear predictive control theory a new nonlinear excitation controller is designed for machine infinite excitation control system. This system takes the power angle, angular velocity and active as variables, with generator rotor angular velocity of the output function ,using Adams fourth-order prediction method with expanded output function, and than optimize online scroll, finally, the prediction excitation control law is founded out successfully. Compared with Taylor series method, the simulink results show that this method not only can improve the mechanical stability of the generator, but also improve the dynamic characteristics of the generator terminal voltage, achieved good dynamic character.

TM571

A

1000-3983(2016)03-0050-04

2014-12-11