基于雙MRF模型的夜間圖像增強方法

趙宏宇，肖創柏，禹晶

?

基于雙MRF模型的夜間圖像增強方法

趙宏宇，肖創柏，禹晶

(北京工業大學計算機學院，北京，100124)

為了獲得更理想的夜間可視效果，通過分析Retinex算法在圖像增強時存在的問題，提出一種基于雙馬爾科夫隨機場(MRF)模型的單幅夜間圖像增強算法。該算法首先在HSV顏色空間下構造邊緣保持的Gaussian-MRF模型對照度分量進行估計，根據Retinex原理獲得僅包含物體本身特性的反射分量，并通過增益補償方法對亮度進行恢復與校正，然后構造Huber?MRF模型對增強結果進行優化，經過顏色空間轉換后，最終實現夜間圖像的增強。研究結果表明：本文算法增強效果顯著，能夠有效地凸顯邊緣細節信息，恢復圖像的真實顏色，抑制暗區域噪聲，削弱“光暈偽影”的影響，改善夜間圖像質量。

MRF；Retinex原理；圖像增強；HSV顏色空間；Huber?MRF模型

在夜間環境下，計算機視覺監控設備采集的低照度圖像嚴重退化，可視性較差，不僅信噪比和對比度都較低，甚至會出現較明顯的顏色偏移和失真，大大降低了應用價值，因此，研究夜間圖像增強算法具有重要的實際意義。夜間圖像增強技術的目標是恢復場景的真實色彩和細節，并將圖像調整到更適合人眼觀察和計算機分析處理的范圍，主要包括圖像融合的方法和傳統的圖像增強方法。圖像融合主要應用在近紅外或微光成像技術方面，需要在同場景下采集多幅不同頻譜的圖像，算法復雜耗時，難以滿足人們的實時要求；傳統的圖像增強方法能夠適用于單幅圖像的視覺效果改善上，可應用在彩色圖像、非固定視角等多種場合，主要方法包括直方圖的方法、同態濾波、基于Retinex理論[1?7]的方法(后面簡稱Retinex算法)、基于小波的方法等。其中，Retinex算法對于處理夜晚、大霧等低可視度圖像都有不錯的效果，因而有著廣闊的應用前景。Retinex理論是由LAND等于20世紀70年代提出的一種基于人類視覺的光亮度和色彩感知模型[1]。由于Retinex算法具有高動態范圍壓縮，局部對比度增強，保持圖像色彩恒常性等特點，所以引起了大量國內外學者的興趣。LAND于1986年提出了最早的中心環繞(center/surround)Retinex算法，在此基礎上，JOBSON等[2?3]提出了單尺度Retinex(single-scale Retinex，SSR)算法和多尺度Retinex(multi-scale Retinex，MSR)算法。鑒于Retinex算法存在顏色失真的問題，JOBSON等[4?5]隨后提出了具有顏色保持能力的多尺度Retinex(multi-scale Retinex with color restoration，MSRCR)算法，該算法能夠在擴大圖像動態范圍壓縮的同時，實現顏色保真。KIMMEL等[6]通過顏色空間的轉化解決顏色失真的問題，提出了一種基于變分框架的Retinex算法。為了提高細節的顯示效果，ELAD[7]提出了基于雙邊濾波(Bilateral filter)的Retinex算法，該算法在保持圖像細節的同時可以很好地消除光暈效應的影響。此后，基于Retinex原理的圖像增強算法相繼被提出，在效果與效率方面都有提高[8?10]。目前對于夜間等低照度圖像的增強方面，Retinex算法普遍存在噪聲放大、高對比度邊緣區域存在“光暈偽影”和顏色失真等問題。本文作者通過分析Retinex算法產生誤差的原因，模擬人類視覺和大腦對圖像的感知和理解的方式，提出了一種基于雙馬爾科夫隨機場(MRF)的夜間圖像增強算法。該算法在HSV(hue, saturation, value)顏色空間下僅對亮度圖像進行處理，避免顏色失真；構建具有保邊能力的Gaussian-MRF模型[11]對照度分量進行估計，消除“光暈偽影”現象；根據Retinex原理獲得反射分量，并通過增益補償(gain/offset)方法對亮度進行恢復與校正；由于人類視覺對低頻區域的噪聲干擾比高頻區域更加敏感，因此，構建Huber?MRF模型[12?13]對增強結果進行優化，在抑制噪聲的同時保留有效細節信息；最后經過顏色空間逆變換操作完成對圖像的增強處理。本文算法能夠克服Retinex算法處理夜間低照度圖像時存在的多類問題，實現對較暗區域的動態范圍進行拉伸，增強可視度，處理后的圖像整體協調自然，更加符合人類觀察特點。

1 Retinex理論與存在的問題

Retinex理論認為1幅圖像可分為2部分，即1幅圖像可由反射分量和照度分量的乘積表示，

式中：表示圖像像素。照度分量的性質取決于光照的照射源，決定了圖像中像素能達到的動態范圍；反射分量的性質則取決于成像物體的特性，包含場景細節信息。Retinex原理的思想實際上就是去除或減少照度分量的影響，獲得包含較多細節信息的反射分量。其計算過程在對數域上進行：

上述反射分量的求解在數學上是一個奇異問題，因此需要把求解問題變成約束最優化問題，通過對照度分量的準確估計進行反射分量的求解。本文采用中心環繞的方法對照度分量進行估計，中心環繞的方法假設每個像素的灰度值都受到來自周圍環繞像素的影響，表示如下：

其中：*代表卷積操作；()為環繞函數，一般采用高斯函數。為了保留更多的圖像細節，環繞函數多選擇具有保邊能力的平滑濾波[7]形式。

Retinex算法計算相對簡單，但是在夜間圖像的增強方面容易出現多類問題。本文將對直接影響反射分量求解的因素進行分析，首先分析照度分量估計的誤差Δ對于反射分量的影響，得到反射分量的求解誤差為

式中：ρ為反對數函數；Δ為計算反射分量的誤差。

由式(4)可知：Δ對于反射分量的準確求解具有一定的影響，但是并不是隨著Δ的增大而Δ也明顯增大。實際上，只有當Δ很大時，才會對Δ造成 影響。

考慮到圖像中不可避免地存在著噪聲干擾，設圖像噪聲為，分析噪聲對反射分量計算的影響。

由式(5)可知：對于位于低灰度區域，處理后的結果噪聲得到放大。根據式(4)可知：這些位于原圖該區域的噪聲基本不受到照度分量估計的影響。

以SSR算法為例，其環繞函數選擇接近人眼感知的高斯函數形式：

其中：1為常數；為尺度參數，用于調控平滑程度；(，)為圖像二維坐標。首先采用不同高斯核(見圖1(c)和(d))對1幅具有較低動態范圍的低照度圖像進行增強，見圖1(a)。當較小時，低照度圖像增強處理后的細節部分能較好地凸現出來，圖像有一定程度上的顏色失真，見圖1(e)；反之，當較大時，獲得的圖像顏色保真度高，改善了低照度部分的亮度和對比度，但是出現了細節損失的情況，這在高亮區域尤為突出，見圖1(f)。隨著尺度參數的增加，獲得的增強結果趨于穩定，不產生大的變化，這與上述對式(4)的分析結果相符。

進行對于夜間圖像增強處理的實驗，結果見圖1(b)。隨著尺度參數增加，圖像可視度得到提升；當增大到一定程度時，最終在一些暗區域(如天空區域等)出現了噪聲放大的現象，此時的變化趨勢與噪聲的強度變化相互獨立，如圖1(g)和(h)所示，這也與上述對式(4)和(5)的分析結果相符。同時，夜間圖像受到非自然光源的影響，處理后的圖像的高亮區域也會被放大，出現“光暈偽影”現象，如圖1(g)和(h)所示的樓房燈源附近。

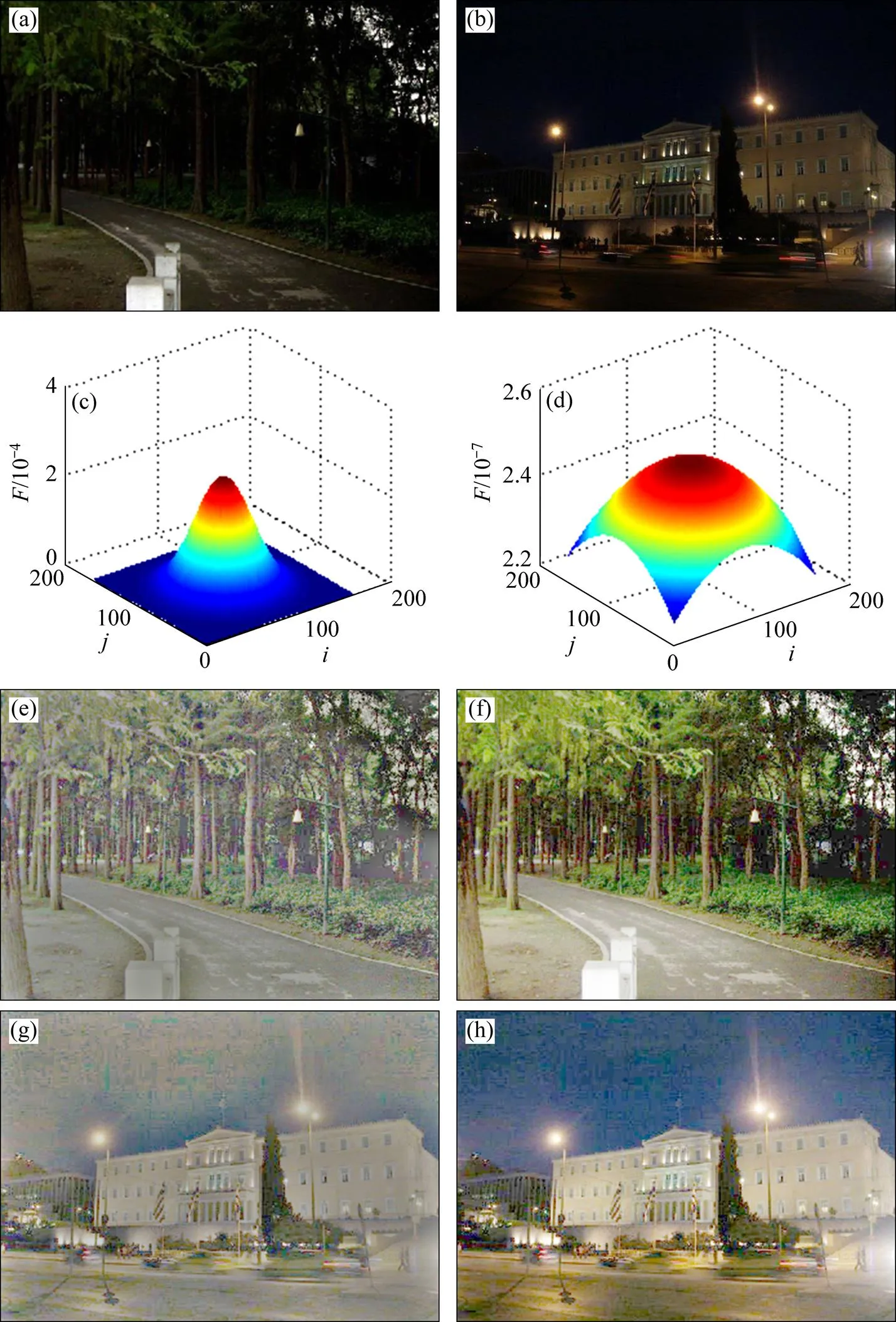
(a) 低照度圖像；(b) 夜間圖像；(c) 尺度較小的高斯核；(d) 尺度較大的高斯核；(e) 由圖1(a)得到的小尺度增強結果；(f) 由圖1(a)得到的大尺度增強結果；(g) 由圖1(b)得到的小尺度增強結果；(h) 由圖1(b)得到的大尺度增強結果

針對Retinex算法在圖像增強方面存在的上述問題，本文主要對照度分量的估計與反射分量的優化2方面進行研究。求解照度分量時，將在保持邊緣細節的基礎上對局部進行平滑，力求提高圖像低照度區域的可視度，并保持其高亮區域的細節信息；同時，對獲得的反射分量結果進行優化，保持細節信息的前提下削弱噪聲的強度。

2 本文算法

本文提出一種基于雙MRF模型的單幅夜間彩色圖像增強算法，該算法可分為3步：1) 進行顏色空間轉化，將夜間彩色圖像由RGB顏色空間轉換到HSV顏色空間，獲得圖像在HSV顏色空間下的亮度圖像，構建邊緣保持的Gaussian-MRF模型估計圖像照度分量，根據Retinex原理獲得其反射分量；2) 采用增益補償方法進行亮度恢復與校正；3) 構建Huber-MRF模型優化增強后的結果，將圖像由HSV顏色空間轉換到RGB顏色空間，最終得到理想的增強圖像。

2.1 顏色空間轉換

Retinex理論的應用前提是灰度世界假設(gray-world assumption)。在實際應用中，Retinex算法對于彩色圖像的增強處理一般是在圖像的R，G和B 3種顏色通道下分別進行，不同通道的不均衡增強容易造成圖像顏色失真，且需要執行3次，時間復雜度較高。因此，本文選擇在彩感知上更加接近人類視覺期望值的HSV顏色空間代替RGB顏色空間，將原圖像轉換到HSV顏色空間下，得到飽和度圖像s、色調圖像H和亮度圖像V，這里僅對亮度圖像進行增強處理。

2.2 基于Gaussian-MRF模型的照度分量估計

由于照度分量具有局部平滑的特性，本文構造具有保邊平滑能力的Gaussian-MRF模型對原圖進行平滑操作，從而估計出照度分量。該模型用于計算下述最大后驗估計(MAP)問題：

式中：V和V分別為原圖像的亮度圖像和亮度圖像對應的照度分量；(V)為先驗概率，反映將要求解的V應具有的性質；(V|V)為似然函數，表示圖像噪聲服從的分布，MAP目標就是在滿足最大后驗概率的條件下求出圖像照度分量的估計值。該MAP問題的求解可以表示為最小化如下能量函數：

該MRF模型的數據項定義如下

式中：為圖像的像素集合；g為與1有關的噪聲分布函數，本文采用高斯分布，即g()=2。

該MRF模型的平滑項定義如下：

式中：為像素的相鄰像素集；s為關于V的約束函數；本文取，為函數的平滑項上限，防止由于平滑項過大造成的邊緣模糊的現象；1()為權值函數。該平滑項表示對相鄰像素間一致性的約束，認為若像素處于同一深度，則它們的灰度越相似。

Retinex算法往往選擇參數固定的濾波器對整幅圖像進行照度分量估計，未考慮到光在場景傳播時的指數衰減性，造成了圖像增強效果層次性較差、細節損失的情況。雖然MSR和MSRCR等采用多尺度的方法克服細節恢復能力的不足，但是提高了算法的時空復雜度，且包含的參數較多。因此，需要在照度分量計算過程中考慮到場景信息的指數衰減性。式(10)中，設置權值函數為，函數本身包含場景的深度信息，具有指數衰減的特性。設置權值的目的是力求增加低照度區域的平滑程度，并通過增加可視度較高的區域數據項的權重，在求解過程中保持已知場景的細節信息。

傳統的SSR，MSR和MSRCR等算法在圖像明暗對比強烈處易產生光暈現象，原因在于其對于光照平緩變化的假設。本文的Gaussian-MRF模型能夠在實現局部平滑的同時較好地保持圖像細節信息，避免由于高亮區域邊緣過于平滑從而導致“光暈偽影”現象的產生。

2.3 增益補償

當獲得理想的照度分量V后，根據式(2)即可獲得反射分量。此時，一般整體亮度偏暗，且對數域中的計算經常會出現負值，需要通過進一步調整以提高圖像質量，本文采用增益補償的方法對圖像亮度進行恢復與校正，即

2.4 基于Huber?MRF模型的優化操作

夜間圖像中存在著較多的噪聲，尤其是位于暗區域的物體存在較低的信噪比，在增強處理之后這些噪聲也可能同時被放大。采用基于隨機場模型的降噪技術能克服傳統圖像恢復方法的不足。因此，本文通過構建Huber?MRF模型來優化反射分量結果，采用MAP作為最優化準則，力求在保持邊緣信息的前提下抑制噪聲。與2.2節中相似，該MRF模型來自如下的能量函數：

該MRF模型的數據項定義為

式中：V為目標圖像；2為尺度參數。

該MRF模型的平滑項定義如下：

式中：h為由Huber函數，

式(15)通過閾值把函數分為線性和二次型2部分，既保護了邊緣，又由凸性保證了MAP估計的有效性。當||≤時，實際轉化成了Gaussian?MRF模型，此時的二次型形式保證了局部平滑特性；當||＞≥0時，線性形式保持了圖像的邊緣特性。為斜率，用于調節保邊程度。噪聲等現象所處的局部背景亮度具有掩蓋效應，亮度越大，噪聲可見度越低，本文根據該特性，自適應調整Huber函數線性部分的斜率，以達到根據場景情況，合理地進行抑制噪聲和保持邊緣操作。定義為

式中：2為常數，用于調節斜率的影響強度。

在Huber?MRF模型下優化反射分量結果，不僅可以有效地抑制天空、遠景等暗區域的噪聲，而且能夠減小圖像邊緣振蕩，保持有效邊緣細節。

當求解出理想的V后，結合飽和度圖像s與色調圖像H，將圖像由HSV顏色空間變換轉化到RGB顏色空間即可得到最終的增強圖像。

2.5 MRF模型的求解

MRF方法中尋求能量函數的最小解問題，可采用條件迭代模式(iterated conditional model，ICM)[14]、置信度傳播(belief propagation，BP)、模擬退火(simulated annealing，SA)、基于Graph Cuts的alpha-expansion[15]等方法來實現。其中，ICM方法是一種易于操作的方法，具有較高的魯棒性與可擴展性，本文采用ICM方法尋求能量函數的最優解。

本文的Gaussian-MRF模型力求在保持主要細節信息的同時，盡量對局部進行平滑，而Huber?MRF模型則是為了在平滑暗區域噪聲的同時盡量保留細節信息。前者迭代次數1一般為3~10次，后者迭代次數2僅需要1~3次即可獲得理想結果。

3 實驗仿真與分析

本文在Matlab平臺(CPU intel雙核主頻2.66 GHz)上對多幅彩色夜間圖像進行分組實驗，分別從主觀視覺效果和圖像質量客觀評價2方面對其進行實驗分析。本文將與多種基于Retinex原理的算法進行比較，包括SSR，MSR和MSRCR算法和ELAD等[7]提出的基于雙邊濾波的Retinex算法。算法的主要參數設置包括：1) SSR參數參考[2]；2) MSR參數參考[3]；3) MSRCR的3個高斯尺度參數為1=15，2=80，3=250，其他參數參考文獻[4]；4) ELAD算法的雙邊濾波參數為l=5，s=100，r=0.3，Gamma參數為=5，其他參數參考文獻[7]；5) 本文算法包含的參數設置為1=200，1=0.1，min=0.8，=1.2，=2，=0，2=200，2=0.02，1=10，2=3。

在圖像質量客觀評價方面，本文采用圖像均值、標準差、熵、邊緣保持指數、直方圖的相似度、峰值信噪比等評價指標對5種算法進行評價。均值用于評價圖像平均亮度的變化，其值越大表示亮度提高越大；標準差用于評價圖像的對比度，其值越大表示對比度越高；熵用于衡量圖像的信息量，其值越大表示圖像包含的信息越多；邊緣保持指數用于衡量邊緣的保持能力，其值越大表示其保持邊緣能力越強，凸顯細節能力也越強；直方圖的相似度采用直方圖的交來計算增強前后圖像的RGB顏色直方圖形狀的相似程度，其值越大表示直方圖越相似，算法的顏色保真能力越強；PSNR用于評價圖像增強后噪聲干擾情況，峰值信噪比值越大則表示抑制噪聲的能力越強。

圖2和圖3所示為對真實場景下夜間彩色圖像的增強處理實驗，原圖尺寸分別為550×400和512×384，其中，圖2(b)~(f)所示分別為5種算法對圖2(a)增強后的結果，圖3(b)~(f)所示分別為5種算法對圖3(a)增強后的結果。表1和表2所示為其對應的客觀評價結果。圖4所示為對模擬圖像增強的比較實驗，原圖尺寸為512×512。圖4(b)所示為圖4(a)添加噪聲后的結果，圖4(c)所示為圖4(b)添加70%透明度的陰影得到的結果，圖4(d)~(h)所示分別為5種算法對圖4(c)增強后得到的結果，表3所示為其對應的客觀評價結果。由于Retinex算法處理低照度圖像后，結果普遍存在泛白效果，圖像整體亮度得到不同程度地提升。而亮度的變化為評價算法的重要指標，其值不同造成比較分析困難。因此，在對圖3(a)增強的實驗中采用線性調節的方法對實驗結果亮度進行統一，即使其亮度近似相等，通過其他指標的比較進一步說明本文方法的優勢。

由表1~3可知：5種算法在一定程度上提高了均值，說明它們都在一定程度下增強了圖像的亮度。由表1~3中的熵值與標準差值的分析可知：本文算法具有較強的對比度提升能力，并能夠較好地豐富圖像信息。同時，通過對表1與表2的EPI的觀察，本文算法在保持邊緣、凸顯圖像細節等方面均強于其他幾種算法。同時，圖2與圖4的實驗證明了SSR，MSR和MSRCR處理的結果容易出現泛白的現象。圖3雖然對圖像亮度進行了一定的調節，但是在亮度下降的同時，其他指標也跟著下降，圖像質量并未得到顯著改善。

(a) 原圖；(b) SSR算法處理的結果；(c) MSR算法處理的結果；(d) MSRCR算法處理的結果；(e) ELAD算法處理的結果；(f) 本文算法處理的結果

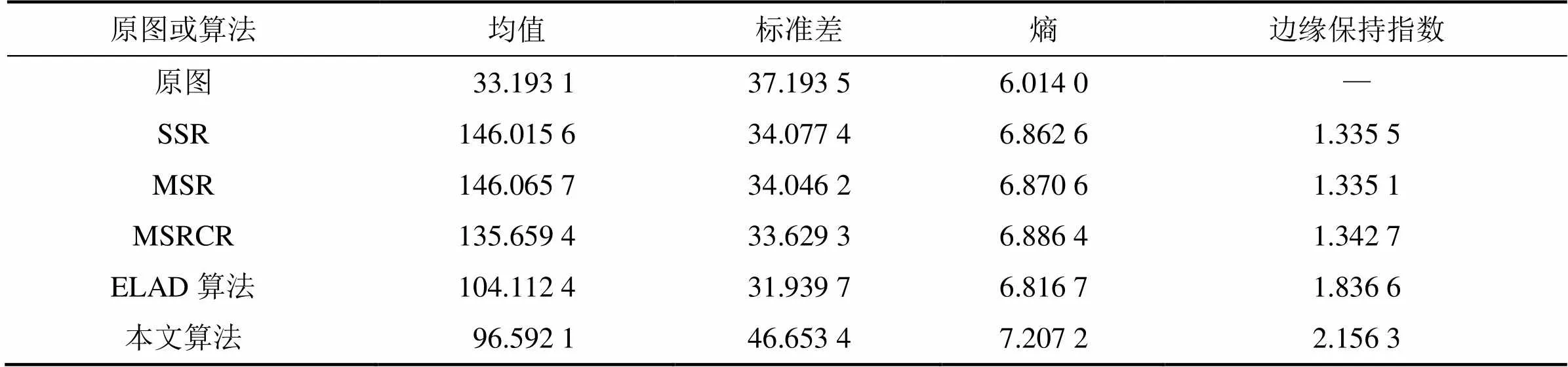
表1 圖2的客觀評價

(a) 原圖；(b) SSR算法處理的結果；(c) MSR算法處理的結果；(d) MSRCR算法處理的結果；(e) ELAD算法處理的結果；(f) 本文算法處理的結果

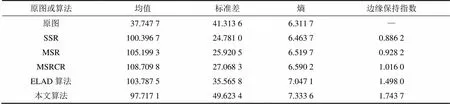
表2 圖3的客觀評價

本文算法與MSRCR均能夠獲得與原圖更加接近的顏色效果，其增強效果更加明顯，如圖2(d)和(f)與圖3(d)和(f)所示，說明本文算法與MSRCR均具有較強的顏色保真的能力。

通過對PSNR的比較分析可知：MSRCR抑制噪聲方面比本文方法要好，但其環繞函數不具有邊緣保持能力，因此，在一些較亮區域附近出現了“光暈偽影”現象，見圖2與圖3所示的燈光周圍；而ELAD算法雖然消除了“光暈偽影”的影響，但其抑制噪聲能力相對較弱，且在圖像邊緣出現了過度增強的現象；與之相比，結合主觀觀察分析，本文算法能夠在保持良好細節信息的前提下抑制噪聲的放大，削弱了“光暈偽影”的影響。

(a) 原圖；(b) 加噪聲圖像；(c)加噪聲加陰影圖像；(d) SSR算法處理的結果；(e) MSR算法處理的結果；(f) MSRCR算法處理的結果；(g) ELAD算法處理的結果；(h) 本文算法處理的結果

表3 圖4的客觀評價

總之，實驗證明了本文算法與其他幾種算法相比，可以很好地校正圖像亮度，具有較強的對比度增強、細節恢復、顏色保持與抑制噪聲等能力。

4 結論

1) 通過分析Retinex算法在圖像增強時出現誤差的原因，構造邊緣保持的Gaussian?MRF模型對照度分量進行估計，較好地保持了細節信息，削弱了“光暈偽影”的影響。

2) 本文算法在HSV顏色空間下執行，使增強后的圖像能很好地保持原有圖像的顏色信息，避免了顏色失真的發生。

3) 針對暗區域噪聲放大問題，通過構建Huber?MRF模型來優化反射分量結果，在保留細節信息的同時抑制了噪聲，進一步提高了夜間圖像質量。

參考文獻：

[1] BANIC N, LONCARIC S. Light random sprays Retinex: exploiting the noisy illumination estimation[J]. Signal Processing Letters, IEEE, 2013, 20(12): 1240?1243.

[2] JOBSON D J, RAHMAN Z, WOODELL G A. Properties and performance of a center/surround Retinex[J]. IEEE Transactions on Image Processing, 1997, 6(3): 451?462.

[3] TAREL J, HAUTI N, CARAFFA L, et al. Vision enhancement in homogeneous and heterogeneous fog[J]. IEEE Intelligent Transportation Systems Magazine, 2012, 4(2): 6?20.

[4] JOBSON D J, RAHMAN Z, WOODELL G A. A multi-scale Retinex for bridging the gap between color images and the human observation of scenes[J]. IEEE Transactions on Image Processing, 1997, 6(7): 965?976.

[5] RAHMAN Z, JOBSON D J, WOODELL G A. Retinex processing for automatic image enhancement[J]. Journal of Electronic Imaging, 2004, 13(1): 100?110.

[6] KIMMEL R, ELAD M, SHAKED D, et al. A variational framework for Retinex[J]. International Journal of Computer Vision, 2003, 52(1): 7?23.

[7] ELAD M. Retinex by two bilateral filters[C]//Scale-Space 2005. Hofgeismar, Germany, 2005: 217?229.

[8] CHEN S, BEGHDADI A. Natural enhancement of color image[J]. Journal on Image and Video Processing, 2010, 175203: 1?19.

[9] WANG S, ZHENG J, HU H, et al. Naturalness preserved enhancement algorithm for non-uniform illumination images[J]. IEEE Transactions on Image Processing, 2013, 22(9): 3538?3548.

[10] 肖創柏, 趙宏宇, 禹晶. 基于引導濾波的Retinex快速夜間彩色圖像增強技術[J]. 北京工業大學學報, 2013, 39(12): 1868?1873. XIAO Chuangbai, ZHAO Hongyu, YU Jing. Rapid Retinex algorithm for night color image enhancement based on guided filtering[J]. Journal of Beijing University of Technology, 2013, 39(12): 1868?1873.

[11] PICKUP L C, CAPEL D P, ROBERTS S J, et al. Bayesian methods for image super-resolution[J]. The Computer Journal, 2009, 52: 101?113.

[12] PITCHAY S A, KABáN A. Estimation of the regularisation parameter in Huber-MRF for image resolution enhancement[C]// IDEAL. Berlin, 2013: 294?301.

[13] KABáN A, PITCHAY S A. Single-frame image recovery using a Pearson type VII MRF[J]. Neurocomputing, 2012, 80: 111?118.

[14] BESAG J. On the statistical analysis of dirty pictures[J]. J Roy Statist Soc B, 1986, 48: 259?302.

[15] FIX A, GRUBER A, BOROS E, et al. A graph cut algorithm for higher-order Markov random fields[C]//IEEE International Conference on Computer Vision. Barcelona, Spain, 2011: 1020?1027.

(編輯 楊幼平)

Night color image enhancement based on dual MRF model

ZHAO Hongyu, XIAO Chuangbai, YU Jing

(College of Computer Science and Technology, Beijing University of Technology, Beijing 100124, China)

Through analyzing the errors introduced by Retinex algorithms, a novel enhancement method based on dual Markov random field model(MRF) was proposed to improve single night color image visibility. Firstly, an edge-preserving Gaussian?MRF model to estimate illumination component in HSV color space was constructed. The reflection component obtained by Retinex principle was corrected through gain/offset method. Then, an effective Huber-MRF model to optimize the result was constructed. Finally, after the color space conversion, the proposed method realized the night color image enhancement. The results show that this method has the characteristics of detail preserving, color restoration, Halo effect elimination and noise suppression, and can enhance night color image visibility robustly.

MRF; Retinex principle; image enhancement; HSV color space; Huber?MRF model

10.11817/j.issn.1672-7207.2016.10.011

TP394.1

A

1672?7207(2016)10?3361?08

2015?10?15；

2016?01?08

北京市教委科技發展重點項目(KZ01210005007)；北京市教育委員會科技發展計劃項目(KM201310005020) (Project(KZ01210005007) supported by Science and Technology Development Plan Key Project of Education Commission of Beijing Municipal; Project(KM201310005020) supported by Science and Technology Development Plan Project of Education Commission of Beijing Municipal)

趙宏宇，博士，從事計算機視覺與圖像處理研究；E-mail：asas.014@163.com