復雜電磁環境下組網雷達對隱身目標的跟蹤研究*

李修和，冉金和

(電子工程學院，安徽 合肥 230037)

?

復雜電磁環境下組網雷達對隱身目標的跟蹤研究*

李修和，冉金和

(電子工程學院，安徽 合肥 230037)

在復雜電磁環境背景下，研究了組網雷達基于粒子濾波算法對隱身目標的跟蹤濾波問題，建立了雷達觀測方程和隱身目標的多基地雷達截面積模型，分析了基于UPF的組網雷達目標跟蹤濾波算法。利用計算機仿真驗證了復雜電磁環境下組網雷達利用粒子濾波技術跟蹤隱身目標的有效性，并對幾種跟蹤算法的效率進行了比較。

組網雷達；目標跟蹤；粒子濾波；仿真

0　引言

信息技術的迅猛發展和其在軍事領域的廣泛運用，加之對抗雙方圍繞電磁頻譜控制權的爭奪使得戰場電磁環境日趨復雜。戰場空間己方電子設備的密集部署等因素引起的電磁影響和己方電子干擾等形成的電磁威脅，是戰場復雜電磁環境的主要構成因素。組網雷達通過將多部不同體制、不同頻段、不同程式(工作模式)、不同極化方式的雷達或者無源偵察裝備適當布站，借助通信手段鏈接成一個有機整體。作為一種四抗能力(抗電子干擾、抗反輻射摧毀、抗隱身和抗低空突防)較強的新體制雷達，組網雷達對抗隱身目標具有單基或單部雷達無法比擬的優勢。

本文就復雜電磁環境下組網雷達對隱身目標的跟蹤問題進行研究，主要考慮目前存在的兩個現實局限情況：一是目前多目標跟蹤技術大多側重于常規雜波環境，沒有考慮實際的戰場環境對觀測信息的影響；二是復雜電磁環境引起的非線性和非高斯問題異常嚴重，常用的擴展卡爾曼濾波(EKF)、去偏轉換卡爾曼濾波(DCMKF)、無味卡爾曼濾波(UKF)等算法在實際應用中都存在較大缺陷。近年來，隨著計算能力以及統計理論的發展，粒子濾波(PF)算法得到了迅速的發展，在處理非線性非高斯問題中顯示了強大的生命力。粒子濾波算法雖然比較簡單，但在采樣過程中有時會出現比較嚴重的退化現象。UPF是粒子濾波器的一種改進算法，它能夠很好地解決粒子濾波器的退化現象。本文擬采用UKF和粒子濾波結合的UPF算法，研究復雜電磁環境下組網雷達如何綜合利用多個雷達站的觀測信息對隱身目標進行目標跟蹤。

1　復雜電磁環境下對隱身目標觀測方程建模

1.1不同復雜度下雷達觀測方程建模

為了建立復雜電磁環境下雷達的具體觀測方程，將戰場電磁環境的復雜程度等級具體劃分為四級：Ⅰ級電磁環境、Ⅱ級電磁環境、Ⅲ級電磁環境和Ⅳ級電磁環境。

1)Ⅰ級電磁環境

Ⅰ級電磁環境即簡單電磁環境，雷達站在捕獲目標時，基本沒有受到電磁威脅。此時利用雷達站全部的測量數據對目標進行定位跟蹤，對于三坐標雷達，包括測得的目標斜距ri、方位角φi和俯仰角εi；對于二坐標雷達，包括目標斜距ri、方位角φi，它們的表達式如下：

(1)

寫成矩陣形式為：

(2)

此時的測量子集是：Z(k)=(ri,φi,εi)T

2)Ⅱ級電磁環境

Ⅱ級電磁環境即輕度電磁環境，雷達站在捕獲目標時，受到一定的電磁威脅，但電磁威脅的強度比較弱，此時雷達站仍能觀測到全部數據，但由于電磁威脅的影響，測量值偏差比無干擾時明顯增大。

根據相關文獻，認為Ⅱ級電磁環境的判斷條件是雷達接收機端內的信干比滿足：

10lgSj>-3dB

(3)

3)Ⅲ級電磁環境

Ⅲ級電磁環境即中度復雜電磁環境，雷達站受到的電磁威脅增大到一定程度后，將無法給出目標的斜距測量數據，三坐標雷達仍能夠給出目標的方位角φi和俯仰角εi，二坐標雷達仍能給出目標的方位角φi。同樣根據相關文獻，Ⅲ級電磁環境的判斷條件是：

-40dB<10lgSj≤-3dB

(4)

此時，對雷達站而言，測量的子集為Z(k)=(φi,εi)T或Z(k)=(φi)T，并且有如下的表達式：

(5)

寫成矩陣形式，則表達為：

(6)

此時的測量子集是：Z(k)=(φi,εi)T。

4)Ⅳ級電磁環境

Ⅳ級電磁環境即重度復雜電磁環境，雷達站斜距測量數據、方位和俯仰測量數據丟失，該雷達站不提供任何觀測信息參與定位。

綜上可見，在雷達網中雷達由于受不同干擾強度的干擾，各單站可能參與定位的觀測向量有：1)Z(k)=(ri,φi,εi)T；2)Z(k)=(φi,εi)T；3)Z(k)=(φi)T。

1.2隱身目標的多基地雷達截面積(RCS)

組網的雷達采用空間分集的形式，以多發多收的形式存在，當發射機與接收機遠離時，使目標在該多站之間運動，并使兩個站之間夾角(簡稱雙基地角)β≥130°，這樣還可獲得目標前向散射信號，這是實現反隱身的關鍵所在，原因是多基地RCS的增大是由前向散射獲得。例如一個球體的投影面積為A、半徑為r，被波長為λ的電磁波照射時，其前向散射面積為：

(7)

而該球的單基地雷達后向散射面積為：

(8)

(9)

若r/λ=10，則σf/σb=4000(36dB)。故前向散射面積明顯增大。

在基于組網雷達的多基地散射結構中，發射站、目標和接收站構成了一個雙基地角，雙基地角平分線則往往定義為等效波矢量，當雙基地角較小時，等效波矢量可用于更換單基地截面積中的波矢量，以便得出雙基地雷達RCS的較佳近似值。但是當雙基地角較大時(180°≥β≥130°)，就不能用這種近似方法了。其理由如下：1)由于入射方向波矢量決定了散射體的照射與投影區域，故電流積分區域(使用物理理論的情況下)，如用等效波矢量，則可能是極為錯誤的。2)使用高頻漸進技術必須極其謹慎，這是由于等效波矢量的大小隨雙站角度的增大而減小。波數的依次減小意味著目前來自散射體的響應要比局部集中散射更加擴展。3)現有的投影法與發射機和接收機有關。對發射機和接收機，因為往往不是所需要的，所以不能簡單地應用同一投影過程。

對于形狀復雜的物體，通過分析得出了雙基地雷達截面積σb與單基地雷達截面積σm的經驗公式：

(10)

式中，n為經驗參數，一般取n為7～10；β為雙基地角，單位是弧度。

從式(10)可以看出，雙基地雷達的RCS總是大于單基地雷達的RCS。當目標位于低空時，雙基地角可以滿足180°≥β≥130°的條件，從而獲得較大的RCS。

而對于隱身目標，在計算其單基地雷達的RCS時，考慮機翼是主要的鏡面散射體，它的RCS值最大,但其大后掠角卻使雷達設計者最關心的飛機迎頭方向的RCS顯著減小。當雷達以小仰角觀測迎面飛來的飛機時，機翼的前沿可被近似看作一段圓柱體，法線方向照射時，單側機翼RCS的方向圖為：

(11)

式中，λ為雷達波長,D為直徑(對應翼厚),L為柱體長(對應翼長),θ為偏離機翼法線的角度。機翼后掠角為φ，飛機的方位角為α。

2　復雜電磁環境下基于UPF的組網雷達目標跟蹤濾波算法研究

復雜電磁環境下，如組網雷達中網內大部分雷達受到壓制性干擾，單站雷達的距離信息就會喪失，無法在單站對目標進行定位濾波而形成航跡，此時就不能夠應用分布式航跡融合方式，組網雷達將被迫采取傳送單站觀測信息到融合中心進行處理的方式，結合多個雷達的信息來對目標進行濾波跟蹤。近年來有很多文獻對組網雷達目標跟蹤進行了研究，但大都假定了所有傳感器同步采樣，或者沒有通信延遲。實際上，傳感器常常是異步工作，而且采樣速率不等，通信延遲不同。因此，在非線性非高斯環境，組網雷達系統中部分傳感器受到干擾而測量信息不全，且組網雷達異步工作時，如何充分利用“殘留”的信息對目標進行融合跟蹤，是非常必要且十分重要的問題。

2.1量測數據的串行合成

組網雷達系統中各傳感器異步掃描，每次掃描周期結束時，將此次掃描的觀測量附帶時間送到中心進行處理。

以兩部雷達為例，設雷達1和雷達2的掃描周期都為T，但兩者不同步，測量集合D1={Z1(k)|k=1,2,…}和D2={Z2(k)|k=1′,2′,…}，采樣時間之間的關系如圖1所示。

圖1　集中式雷達數據流合成圖

對合成序列{Z(l)|l=1,1′,2,2′,…}，實際上存在2個采樣周期T1、T2，且有T=T1+T2。推廣到多雷達情形，為不失一般性，設組網雷達由m部采樣周期相同的異步工作的雷達組成，對同一目標的測量集合分別為Di={Zi(k)|k=1,2,…;i=0,1,2,m-1}，則對合成的觀測序列有：

(12)

2.2UKF和粒子濾波結合的UPF算法

對經過量測合成之后的測量數據，本文采用UPF算法對其進行濾波處理。粒子濾波不受非線性、非高斯濾波問題的限制，因而得到了廣泛的應用。粒子濾波中的一個關鍵是提議分布。目前，有許多不同的提議分布，最常見的方法是直接采用先驗概率密度函數作為重要密度函數。這種做法直觀而且易于實現，缺點是沒有考慮使用新的觀測值，因而具有一定盲目性，導致最終濾波效果一般。

有的學者提出用擴展的卡爾曼濾波來產生重要性概率密度函數。盡管基于EKF的粒子濾波方法在估計性能上有所改善，但由于EKF在模型線性化和高斯假設中引入了過多的誤差，其改進效果不是很明顯。因此本文采用一種新的粒子濾波器即UPF，該方法使用UKF產生重要性密度，其算法主要步驟如下：

1) 初始化(k=0)。根據初始均值和協方差均勻抽取N個粒子。

2) 在每個采樣時刻，對所有的粒子，UKF更新每個粒子的每個Sigma點。在UKF算法中，由于具有噪聲項，需要對狀態進行擴維處理。

①對每一個粒子進行Sigma點采樣，本文使用比例對稱采樣方法。

(13)

式中，γ=(n+λ)1/2，λ=α2(n+k)-n。

(14)

(15)

②預測方程：

(17)

(18)

(19)

(20)

(21)

(22)

③更新方程：

(23)

(24)

(25)

④使用UKF估計的均值和方差作為PF計算權值的提議分布。

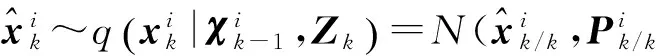
(26)

復雜電磁環境下，觀測噪聲為非正態分布，要代入相應的概率密度函數(即測量噪聲的概率密度函數)進行計算。

對所有粒子計算其權值，并進行歸一化。

⑤輸出k時刻的狀態估計。

3) 重采樣。

(27)

4)遞歸。

返回步驟2)，并令k=k+1。

3　計算機仿真

3.1仿真場景和條件設置

在仿真中設置如下場景：組網雷達由3個三坐標跟蹤雷達組成，以融合中心為坐標原點建立坐標系，如圖2所示。其中雷達2(30km,0,0)為厘米波雷達，雷達1(-15km,30km,0)和雷達3(-15km,-30km,0)為分米波雷達，干擾為遠距離支援干擾且干擾機的工作頻段為10GHz左右，這里我們考慮較強干擾情況，雷達2距離信息丟失，但可以觀測到方位信息。各雷達每次掃描周期結束時，將此次掃描觀測量附帶時間送到中心進行處理。三傳感器異步采樣，取樣時間間隔相差3s，采樣周期取為9s，觀測點數為100。假設目標的初始位置為(80km,0,20km)，初始速度為(-0.1km/s,0,0)。本文對EKF、PF、UPF進行仿真，PF中粒子數目為3000，進行500次蒙特卡羅仿真實驗。

圖2　組網雷達目標跟蹤態勢圖

3.2仿真結果與分析

圖3～5給出了EKF、PF和UPF在觀測噪聲為閃爍噪聲(ε=0.2)情況下目標運動的跟蹤軌跡。圖6～7給出了三種方法估計下的x方向和z方向的均方根誤差。

圖3　EKF跟蹤軌跡(ε=0.2)

圖4　PF跟蹤軌跡(ε=0.2)

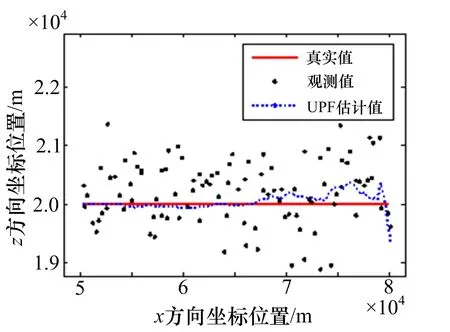
圖5　UPF跟蹤軌跡(ε=0.2)

圖6　x方向位置均方根誤差(ε=0.2)

圖7　z方向位置均方根誤差(ε=0.2)

通過分析仿真結果，可以得到如下結論：

1)在復雜電磁環境下，即使是部分雷達受到嚴重干擾，組網雷達由于空間的分集，也可利用目標的前向散射和量測合成方法， 各站將每次掃描觀測量附帶時間送到中心進行處理，組網雷達可以對抗隱身目標。

2)在閃爍噪聲閃爍強度弱的情況下，組網雷達利用EKF、PF和UPF三種方法均能有效對目標進行跟蹤，隨著閃爍強度的增大，閃爍噪聲概率密度函數同高斯函數差別變大，因此，采用矩匹配的EKF算法誤差明顯變大。PF和UPF算法隨閃爍強度的增大而誤差變化不大。

3)在復雜電磁環境下，系統表現為非線性非高斯，UPF粒子濾波器由于在產生預測粒子時利用了最新的觀測數據，因此對狀態的估計精度要高于標準的粒子濾波器的精度。同時，UPF可以極大地減少PF所用的粒子數，大大縮短了運算時間，與普通的粒子濾波相比，濾波精度和實時性也有很大的提高。

4　結束語

隨著新軍事變革的推進，防空系統中的目標反隱身問題已經成為一道亟待解決的難題。組網雷達在反隱身問題上由于體制上的優越性，受到各國的高度重視。本文利用UKF和粒子濾波結合的UPF算法，研究組網雷達綜合利用多個雷達站的觀測信息對隱身目標進行目標跟蹤的問題，希望能引起相關學術界同行的共鳴，有許多戰場復雜電磁環境下多傳感器數據融合技術的應用和實踐問題值得深入開展研究。■

[1]陳永光, 李修和. 組網雷達作戰能力分析與評估[M].北京：國防工業出版社, 2006.

[2]孫仲康, 周一宇, 何黎星. 單站無源跟蹤技術[M].北京：國防工業出版社, 2008.

[3]李修和. 戰場電磁環境建模與仿真[M].北京：國防工業出版社, 2014.

[4]胡來招. 無源定位[M].北京：國防工業出版社, 2004.

[5]韓崇昭, 朱洪艷. 多源信息融合[M].北京：清華大學出版社, 2006.

[6]Chrzanowski EJ. Radar active countermeasures[M].Artech House, Inc., 1990.

[7]楊振起, 張永順, 駱永軍. 雙(多)基地雷達系統[M].北京：國防工業出版社, 1998.

Research on tracking stealth targets of netted radar in complex electromagnetic environment

Li Xiuhe, Ran Jinhe

(Electronic Engineering Institute, Hefei 230037, Anhui, China)

The problem of netted radar tracking stealth targets based on particle filtering in complex electromagnetic environment is studied. The radar observation equations and the radar cross section of stealth targets in complex electromagnetic environment are established. The tracking algorithm based on unscented Kalman filter of netted radar is analyzed. Simulation results validate the particle filtering technology of netted radar can track stealth targets in complex electromagnetic environment, and some conclusions on the efficiency of tracking algorithms are drawn.

netted radar;target tracking;particle filtering;simulation

武器裝備預研重點基金項目 (9140A33020112JB39085)

2016-06-10；2016-07-11修回。

李修和(1975-)，男，教授，博士，研究方向為戰場電磁環境基礎與應用、信息作戰模擬與仿真及多源信息融合技術等。

TN971;TN974

A