非線性分數階演化方程的新解

劉銀龍，夏鐵成，劉澤宇

（上海大學理學院，上海 200444）

非線性分數階演化方程的新解

劉銀龍，夏鐵成，劉澤宇

（上海大學理學院，上海 200444）

通過使用改進的分數階sub-equation方法尋求一些非線性分數階演化方程的精確解,如分數階Burgers方程、耦合分數階Burgers方程與非線性分數階Klein-Gordon方程等,并得到了這些非線性分數階演化方程的新解.

改進的分數階sub-equation方法；分數階Burgers方程；耦合分數階Burgers方程；分數階Klein-Gordon方程

1695年，萊布尼茲定義了分數微積分-普通微積分的推廣.但直到最近幾十年分數微分方程才重新得到學者們的關注，這是因為其對復雜現象有確切的描述，例如非布朗運動、系統識別、流體流動、控制問題、信號處理、黏彈性材料、聚合物和其他的學科領域的問題.眾所周知分數階方程的最大優勢是其非本地屬性，這意味著未來系統的狀態不僅取決于其當前狀態也取決于其所有的歷史狀態.例如，部分衍生品、流體動力交通模型可以消除由連續交通流的假設［1］引起的缺陷.最近，許多學者開始研究分數階的函數分析，如把Yang-Laplace轉換和Yang-Fourier轉換的性質和定理應用到分數階微分方程、微分系統和偏微分方程等.為了更好地理解復雜的非線性物理現象及其在實際生活中進一步的應用，一個自然而然的問題出現了，即怎樣才能得到分數階偏微分方程（fractional partial differential equation，FPDE）的精確解.目前，已經建立和發展了很多有效的方法，從而獲得了FPDE的數值和分析解，如有限差分法［2］、有限元法、Adomian分解方法［3］、微分轉換方法［4］、變分迭代法［5］、攝動法［6］等.另外，一些偏微分方程已經被研究和解決，如脈沖分數微分方程［7］、分廣義Burgers流體［8］、分數階熱和波動方程［9］等.

最近，He等［10］和Geng等［11］應用Exp-function方法尋求偏微分方程精確解.這種Expfunction方法得到了廣泛的應用，并被用來尋找非線性演化方程的孤波解和周期解，如Maccari系統［12］、Klein-Gordon方程［13］、KdV-mKdV方程［14-15］、Broer-Kaup系統、Kaup-Kupershmidt方程和Toda lattice方程等.這表明，通過Exp-function方法可以得到含參數的解，并且從中可以發現一些大多數現有方法的已知解.張盛等［16］提出了一種新的尋求偏微分方程精確解的直接方法，該方法被稱為分數階sub-equation方法，是基于齊次平衡原則［17］、修正的Jumarie黎曼——劉維爾導數［18］和符號計算.張盛等使用這種方法成功地獲得了非線性分數階演化方程的精確解.眾所周知，當使用直接法找到非線性偏微分方程精確解時，選擇一個適當的擬設是非常重要的.本研究正是通過運用改進的分數階sub-equation方法［19］來尋找在流體力學中分數階方程的精確解.

首先，考慮分數階Burgers方程與耦合分數階Burgers方程［20］：

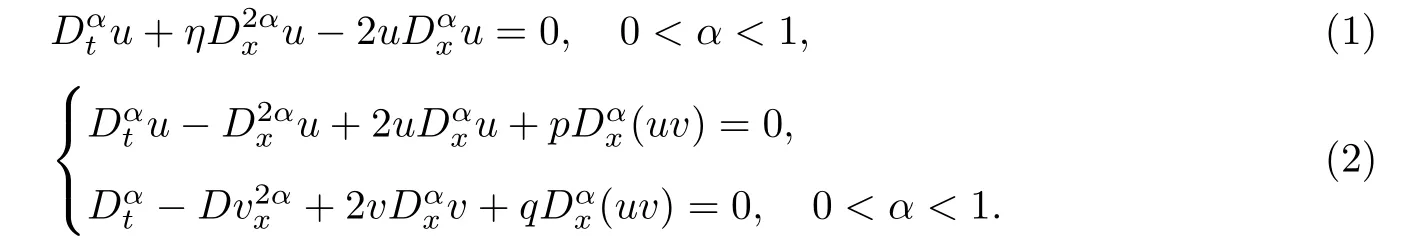
Esipov導出了這個耦合系統.耦合Burgers方程系統的研究是非常重要的，因為這個系統在流體懸浮液或膠體中受到的重力的影響是一個簡單的模型沉降或進化了體積濃度的兩種粒子，其中常量p,q是依賴于系統參數沛克萊數、由重力引起的斯托克斯粒子速度和布朗擴散系數.

另外，嘗試對非線性分數階Klein-Gordon方程［21］

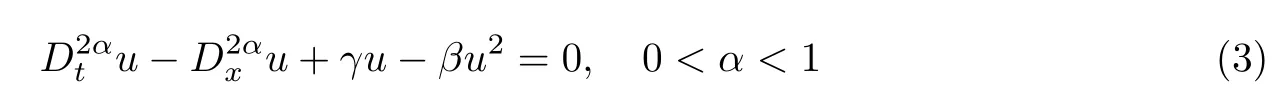
進行了求解，可知非線性分數階Klein-Gordon方程描述了許多非線性類型，且該Klein-Gordon方程在一些實際應用程序中起著重要作用，如固態物理、非線性光學和量子場論等.

修正的α階Jumarie's Riemann-Liouville導數的定義如下：

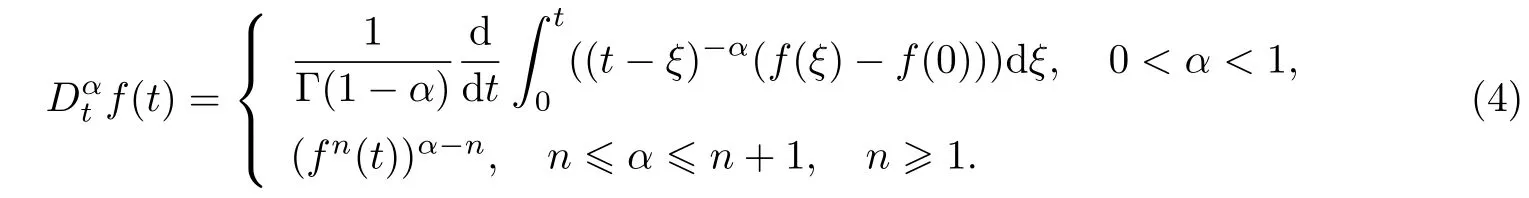
上述定義的分數階導數具有3種性質：

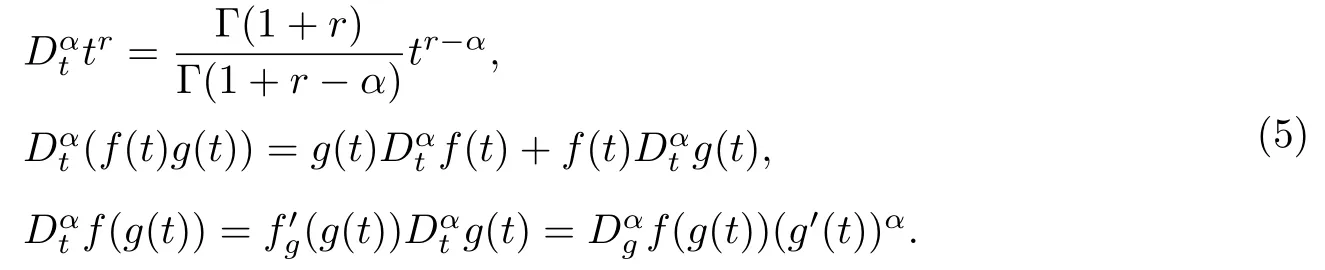
上面的這些性質在后續的分數階方程計算中非常重要.

1 方法介紹

對于改進的分數階sub-equation方法的步驟如下.

步驟1 給定一個分數階偏微分方程，

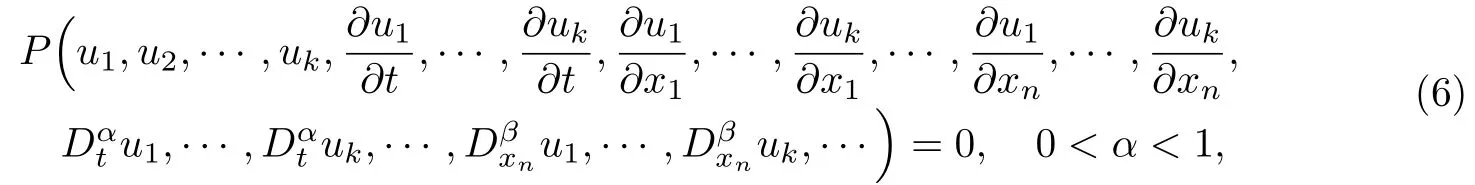
步驟2 通過行波變換

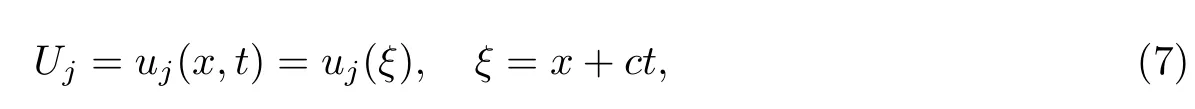
式中，c是待定常數.方程（6）便可以約化成關于Uj=u（ξ）分數階常微分方程

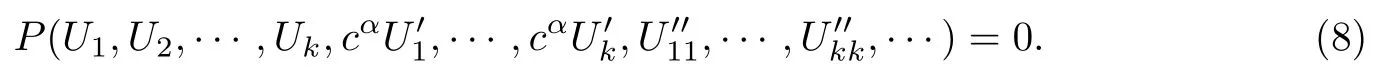
步驟3 假定

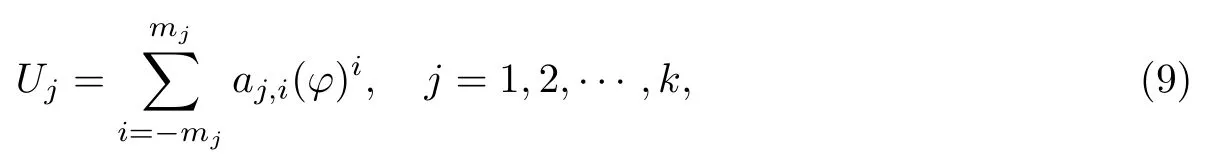
式中，aj,i（i=-mj,-mj-1,…,mj）為待定常數，mj為通過平衡方程（6）或（8）中最高次項與非線性項得到的正數，并且φ=φ（ξ）滿足

這里，

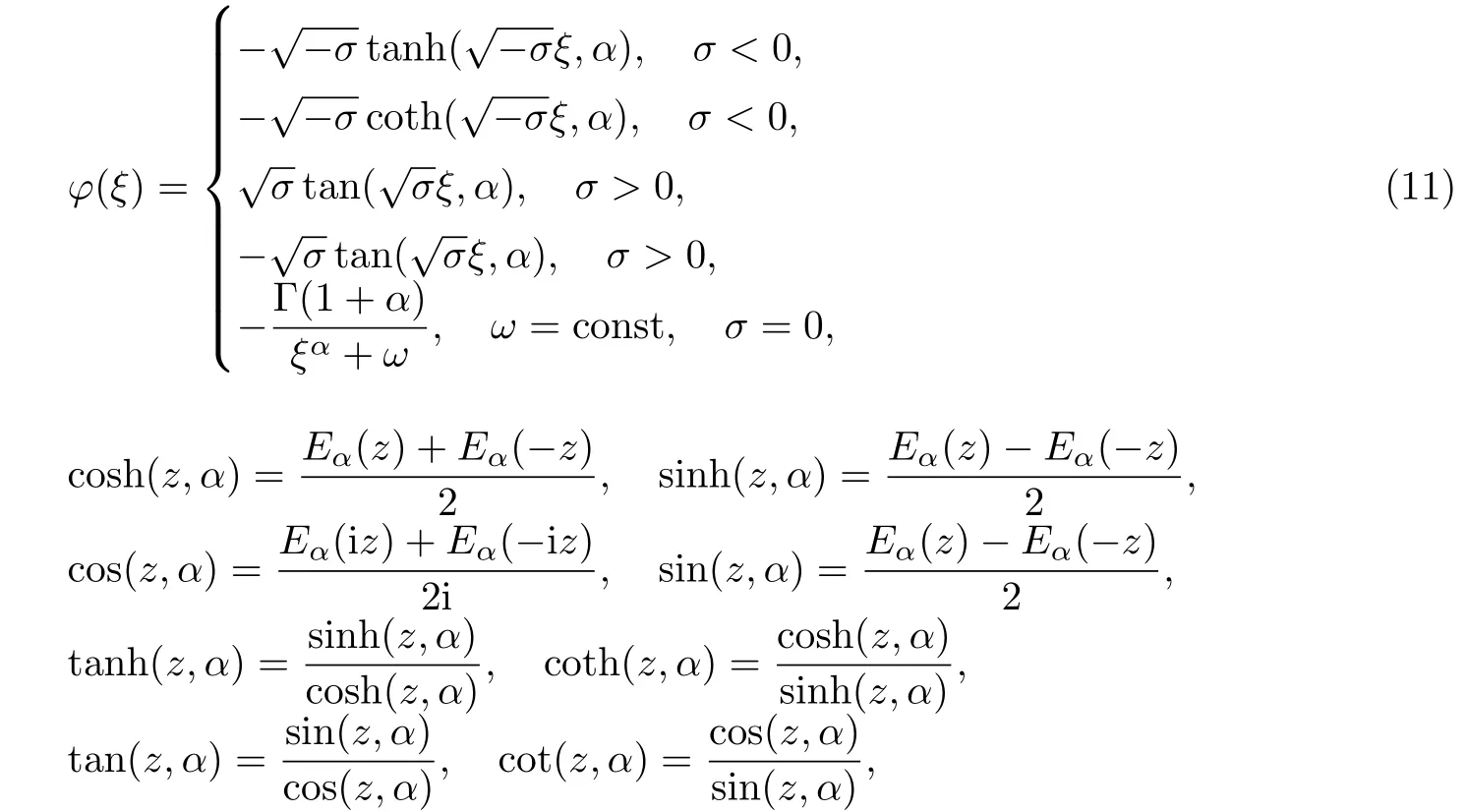
步驟4 把方程（9）和（10）代入方程（8）中，并利用修正的Riemann-Liouville導數的性質［22］，得到一個關于φ（ξ）的多項式.令φ（ξ）k（k=0,1,…,-1,-2,…）的系數為0，得到一組關于c,ai（i=-n,-n+1,…,n-1,n）的超定方程組.

步驟5 假定這些常數c,ai（i=-n,-n+1,…,n-1,n）可以通過上述超定方程組求得，則將這些常數代入方程（9）中就可以得到方程（7）的精確解.

2 應用

下面將用改進的分數階sub-equation方法去求偏微分方程（1）～（3）的解.

2.1 分數階Burgers方程

通過行波變換u=u（ξ）,ξ=x+ct，方程（1）將會被約化成如下的非線性分數階常微分方程：

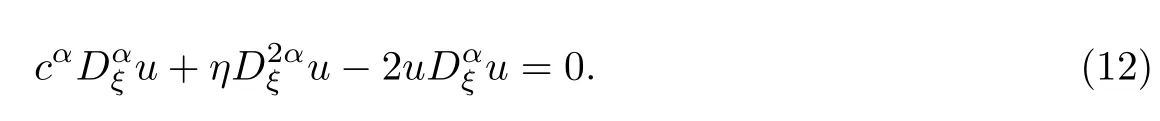
通過平衡方程（11）中最高次項與非線性項，可將解設成

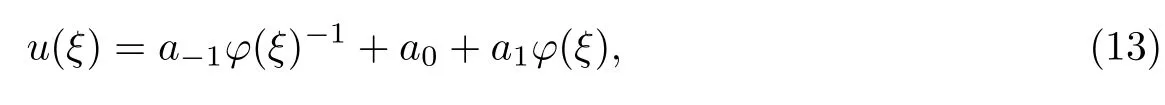
這里的φ（ξ）滿足方程（10）.

將方程（10），（13）代入方程（12），令φ（ξ）i的系數等于0，這樣就可以得到一系列關于c,a-1,a0,a1的超定方程.用Maple計算這組方程，有

情形1

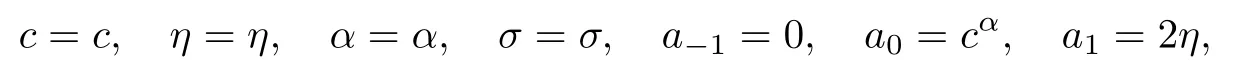
式中，c,α,η是任意的常數.

情形2

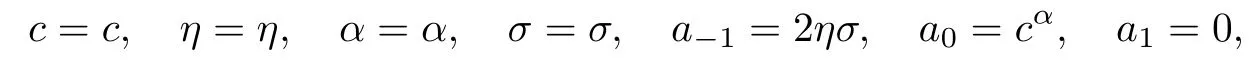
式中，c,α,η是任意的常數.

通過情形1，利用方程（10）和（13）的解可以得到方程（1）的解：

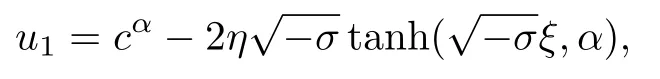
式中，σ＜0,ξ=x+ct.

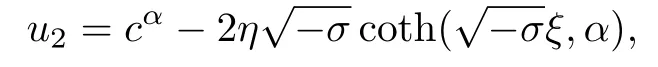
這里，σ＜0,ξ=x+ct.

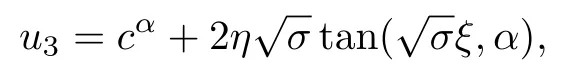
式中，σ＞0,ξ=x+ct.

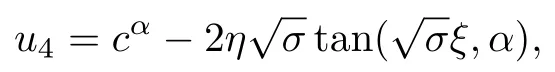
在這里，σ＞0,ξ=x+ct.

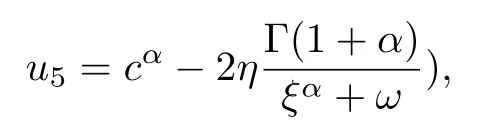
式中，σ=0,ξ=x+ct,ω是常數.

當然，通過情形2可以得到更多的解，這里就不一一列出了.

2.2 耦合分數階Burgers方程

通過行波變換u=u（ξ）,v=v（ξ）,ξ=x+ct，方程（2）將會被約化成如下的非線性分數階常微分方程：

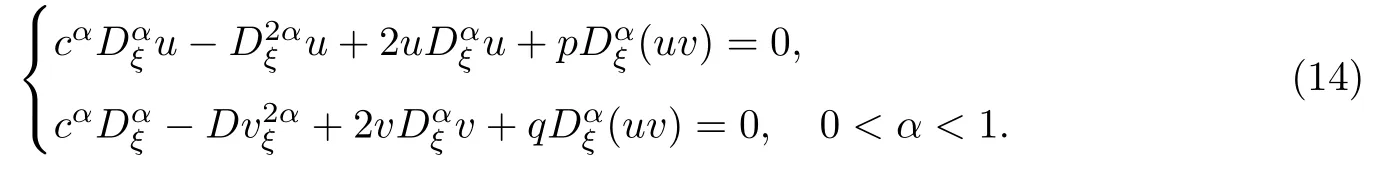
根據前面所描述的方法，可以設方程（14）有如下解的形式：

這里的φ（ξ）滿足方程（10）.

將方程（10）和（15）代入到方程（13）中，令φ（ξ）i的系數等于0，這樣就可以得到一系列關于c,a-1,a0,a1,b-1,b0,b1超定方程組.用Maple計算該方程組，有

式中，η,q,a0是任意的常數.

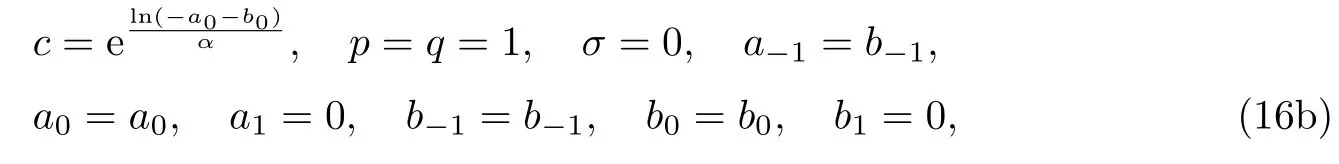
式中，a0,b0,b-1是任意的常數.

利用方程（10），（15）和（16a）的解可以得到方程（2）的解：

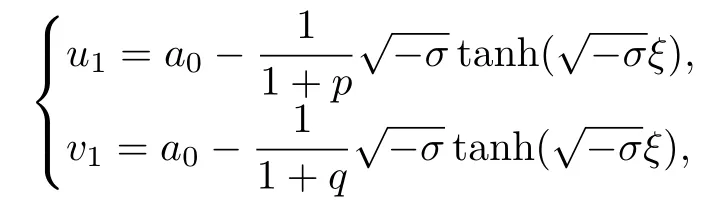
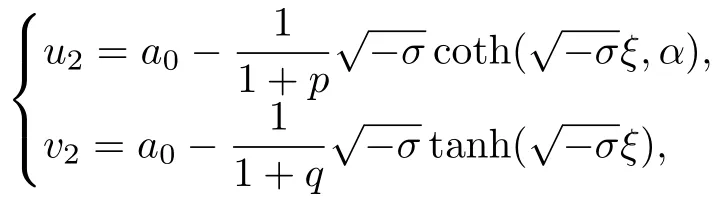
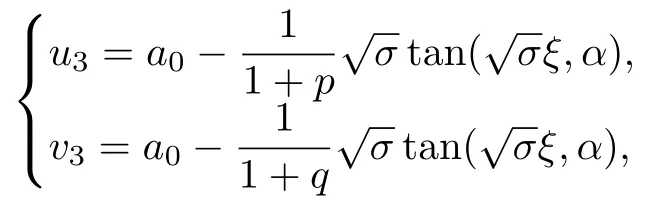
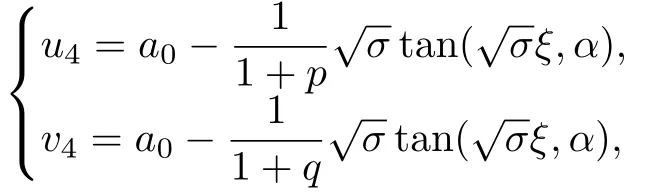
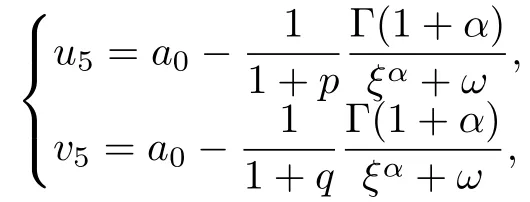
2.3 非線性分數階Klein-Gordon方程

重復上述過程，通過行波變換u=u（ξ）,ξ=x+ct，方程（3）將會被約化成如下的非線性分數階常微分方程：

平衡方程（16）中的最高次項與非線性項，可將解設成

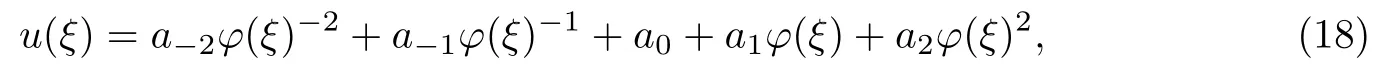
這里的φ（ξ）滿足方程（10）.

將方程（11）和（17）代入方程（16）中，同樣可以得到一組關于c,a-2,a-1,a0,a1,a2超定方程組.用Maple計算這組方程得

利用方程（10），（18）和（19f）的解可以得到方程（3）的解：

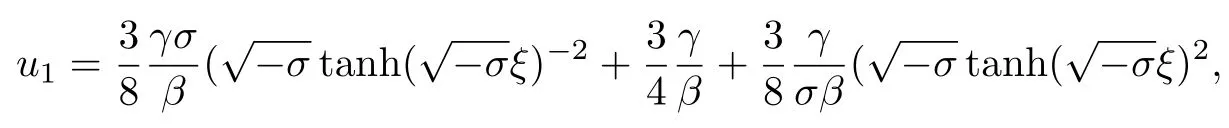
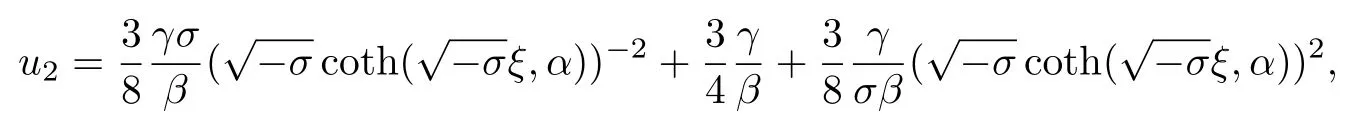
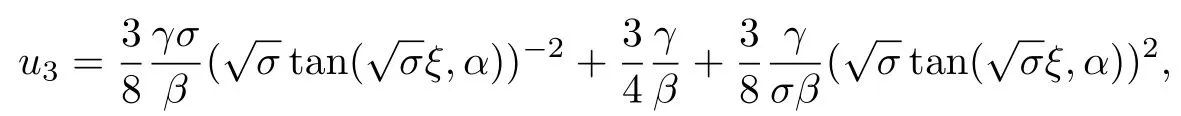
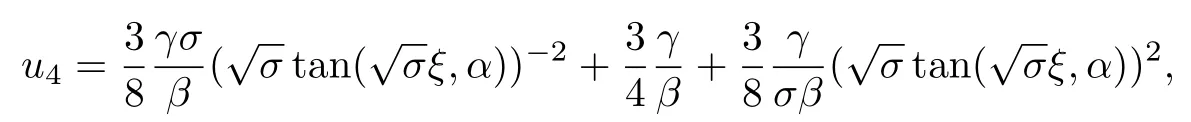
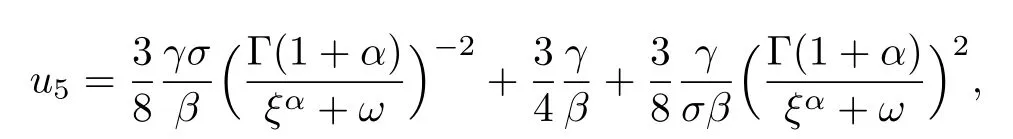
3 結束語

本研究利用一個改進的分數階sub-equation方法解決了在流體力學系統中的非線性偏微分方程，并成功獲得了關于分數階Buregers方程、耦合Buregers方程及分數階Klein-Gordon方程的一些精確解析解.這些解包括廣義雙曲線函數、廣義三角函數的解（目前所知這些解都是新解），而且這些解可能有利于進一步了解復雜的非線性物理現象和偏微分方程.此外，通過使用直接的方法選擇適當的擬設在解決非線性分數階偏微分方程過程中具有重要意義.

［1］HE J H.Analytical solution of a nonlinear oscillator by the linearized perturbation technique［J］.Commun Nonlinear Sci Numer Simul,1999,4（2）：109-113.

［2］CUI M.Compact finite difference method for the fractional diffusion equation［J］.J Comput Phys,2009,228（20）：7792-7804.

［3］EL-SAYED A M A,GABER M.The Adomian decomposition method for solving partial differential equations of fractal order in finite domains［J］.Phys Lett A,2006,359（3）：175-182.

［4］ODIBAT Z,MOMANI S.A generalized differential transform method for linear partial differential equations of fractional order［J］.Appl Math Lett,2008,21（2）：194-199.

［5］HE J H.A new approach to nonlinear partial differential equations［J］.Commun Nonlinear Sci Numer Simul,1997,2（4）：230-235.

［6］HE J H.A coupling method of a homotopy technique and a perturbation technique for non-linear problems［J］.Internat J Non-Linear Mech,2000,35（1）：37-43.

［7］MOPHOU G M.Existence of mild solutions of some semilinear neutral fractional functional evolution equations with infinite delay［J］.Applied Mathematics and Computation,2010,216（1）：61-69.

［8］XUE C,NIE J,TAN W.An exact solution of start-up flow for the fractional generalized Burgers fluid in a porous half-space［J］.Nonlinear Anal,2008,69（7）：2086-2096.

［9］MOLLIQ R Y,NOORANI M S M,HASHIM I.Variational iteration method for fractional heat-and wave-like equations［J］.Nonlinear Anal,2009,10（3）：1854-1869.

［10］HE J H,WU X.Exp-function method for nonlinear wave equations［J］.Chaos Solitons Fractals, 2006,30（3）：700-708.

［11］GENG T,SHAN W R.A new application of Riccati equation to some nonlinear evolution equations［J］.Phys Lett A,2008,372（10）：1626-1630.

［12］ZHANG S.Exp-function method for solving Maccaris system［J］.Phys Lett A,2007,371（1/2）：65-71.

［13］BEKIR A,BOZ A.Exact solutions for nonlinear evolution equations using Exp-function method［J］.Phys Lett A,2008,372（10）：1619-1625.

［14］WU X H,HE J H.Solitary solutions,periodic solutions and compacton like solutions using the Exp-function method［J］.Comput Math Appl,2007,54（7/8）：966-986.

［15］KHANI F,HAMEDI-NEZHAD S.Some new exact solutions of the（2+1）-dimensional variable coefficient Broer-Kaup system using the Exp-function method［J］.Comput Math Appl,2009, 58（11/12）：2325-2329.

［16］ZHANG S,ZHANG H.Fractional sub-equation method and its applications to nonlinear fractional PDEs［J］.Phys Lett A,2011,375（7）：1069-1073.

［17］WANG M.Solitary wave solutions for variant Boussinesq equations［J］.Phys Lett A,1995, 199（1/2）：169-172.

［18］JUMARIE G.Modified Riemann-Liouville derivative and fractional Taylor series of nondifferentiable functions further results［J］.Comput Math Appl,2006,51（9/10）：1367-1376.

［19］GUO S,MEI L,LI Y,et al.The improved fractional sub-equation method and its applications to the space-time fractional differential equations in fluid mechanics［J］.Phys Lett A,2012,376（4）：407-411.

［21］SIRENDAOREJI.Auxiliary equation method and new solutions of Klein-Gordon equations［J］. Chaos,Solitons and Fractals,2007,31（4）：943-950.

［22］ZHOU Y,WANG M,WANG Y.Periodic wave solutions to a coupled KdV equations with variable coefficients［J］.Phys Lett A,2003,308（1）：31-36.

New exact solutions of some nonlinear fractional partial differential equation

LIU Yinlong，XIA Tiecheng，LIU Zeyu
（College of Sciences，Shanghai University，Shanghai 200444，China）

By using an improved method of fractional sub-equation,some nonlinear fractional evolution equations are solved including fractional Burgers equation,coupled fractional Burgers equation and fractional Klein-Gordon equation.New exact solutions of these nonlinear fractional nonlinear evolution equations are obtained.

improved method of fractional sub-equation；fractional Burgers equation；coupled fractional Burgers equation；fractional Klein-Gordon equation

O 178

A

1007-2861（2016）04-0469-08

10.3969/j.issn.1007-2861.2014.05.021

2015-02-13

國家自然科學基金資助項目（11271008）

夏鐵成（1960—），男，教授，博士生導師，研究方向為孤子與可積系統.E-mail：xiatc@shu.edu.cn