基于填充函數—粒子群算法的電力系統無功優化

邱厚明 張向鋒

摘 要 優化和調整電力系統可以促進電力系統經濟和順利的發展，利用無功優化能夠有效的保證電力系統的安全性，在提升供電質量和增加經濟收益的過程中發揮著非常重要的作用。通過電力系統的無功優化應當能夠產生有功損耗降低、電壓質量提升以及電力系統穩定性增加的效果。綜上可以看出對于無功優化的探討有著非常顯著的作用以及效果。

【關鍵詞】電力系統 無功優化 穩定性

對目前所應用的電力系統進行優化通常包含以下幾個特性：首先具有動態性的特點；然后具有多約束和多目標的特點，最后這種優化屬于非線性優化的種類。目前主要有現代人工智能算法以及常規優化算法兩種求解方法。

1 電力系統無功優化方法

粒子群優化算法：這種算法是以下面的思想為基礎的：首先每個離子并不具有重量和體系，在n為搜索空間中以一定的速度進行飛行，其中離子的飛行速度是動態變化的額，變化依據是群體以及個體的飛行經驗。在對粒子適應值進行充分比較的基礎上挑選出比較好的粒子進行復制，這樣能夠有效的提升算法的收斂性。將計算機技術和PSO 算法充分結合起來，提出了一種新的交叉算法形式，然后采用仿真實驗的方法驗證了這種算法的正確性。

填充函數算法：第一步將任意點x0當做一個初始點，采用一些比較有效的局部優化方法對目標函數f（x）的一個局部最優解x*進行求取，第二步，構建與目標函數有緊密關系的局部最優解x*填充函數p（x，x*），并采用局部極小化的方法對p（x，x*）的一個局部最優解x1進行求取，保證x1的函數值f（x1）相比于f（x*）是較優的，然后將通過優化p（x，x*）得到的x1當做新的起始點，接下來從新的起始點重新出發并進行優化f（x），不斷的對以上過程進行重復以保證目標函數值不斷的被優化。如果滿足了相應的終止條件，就把滿足這種條件情況下得到的局部最優解當做近似的全局最優解。通過一些理論和數值研究發現采用填充函數法能夠有效的解決遇到的一些全局最優化的求解問題。

2 無功優化數學模型

必須在滿足相應條件的基礎上才能夠進行無功優化，只有滿足了這些條件才能夠保證系統能夠安全和健康的運行。通常情況下支路電流、節點電壓以及控制變量的限制約束是需要必須滿足的一些條件。

2.1 目標函數

在確定系統的有功調度的基礎上首先應當堅持有功網損最小的原則，然后將負荷節點電壓風參數作為罰函數項來構建下面的目標函數模型：

式中系統的有功網損用PL來表示，負荷節點的電壓、電壓上限以及電壓下限分別用來表示，發電機節點的無功、無功上限以及無功下限分別用來表示，系統負荷節點總數用ND來表示，發電機總數用NG來表示，負荷電壓越界懲罰系數用λ1來進行表示，另外發電機無功出力越界懲罰系數用λ2來進行表示。

2.2 功率約束方程

對于節點的無功功率以及有功功率的處理方法如下，在無功優化模型中可以采用下面的平衡約束方程：

式中，N為電網節點總數；Ui、Uj分別為i、j處的電壓；PGi、PLi分別表示在節點i位置發電機的有功出力以及有功負荷；QGi、QCi、QLi分別表示在節點i位置發電機的無功出力、容性無功補償容量以及無功負荷；Gij、Bij、δij分別表示在電網中節點i和j位置之間的電導、電納以及節點電壓在相位角上所具有的差值。

2.3 變量約束條件

在進行無功優化的過程中通常需要選取四個相應的控制變量，分別為可調變壓器分接頭Tt、容性無功補償容量QC以及發電機端電壓UG，選取了兩個狀態變量，這兩個變量為節點電壓幅值Ud以及電機無功出力QG。

2.3.1 控制變量約束如下：

其中發電機端電壓上、下限值分別用來表示；容性無功補償容量的上、下限值分貝用來表示；可調變壓器分接頭位置的上、下限值分別用來表示。

2.3.2 狀態變量約束方程如下：

3 填充函數-粒子群算法

下面詳細的闡述本文所研究的填充函數-粒子群算法具體優化過程：

第1步：初始化所有粒子（群體規模為N）。在相關限制條件的約束下隨機的確定離子的初始位置以及速度，同時初始位置用pid來進行表示，另外將pgd作為pid中的最優值；

第2步：在完成上面的步驟以后對每個粒子的適應值進行有效的評價，所謂有效值評價指的就是對每個粒子的目標函數值進行計算；

第3步：首先比較每個粒子的歷史最優位置pid以及適應值，通過比較結果來采取相應的措施，當出現優于pid的情況時，就可以將其當做當前的最優位置pid；

第4步：比較每個粒子的群體歷史最優位置和當前最優位置pid比較，當出現優于pgd的情況時，就可以把其當做pgd，然后對pgd的索引號進行重新設置；

第5步：在調整粒子位置以及速度的時候充分的參考粒子群所具有的這些基本信息；

第6步：對終止條件進行檢查，所謂終止條件指的就是具有足夠的適應值以及達到最大迭代次數時的條件，當滿足上面的規定以后就停止整個迭代過程，如果不具有以上條件就返回到第二步中繼續執行。

第7步：充分的應用填充函數算法，其中填充函數的初始值設置為最優解，以局部極小點為開始點得到更優的極小值點，如果算法滿足了相應的終止條件以后將可以將求解得到的極小值點作為最終的全局最優解。

4 算例分析

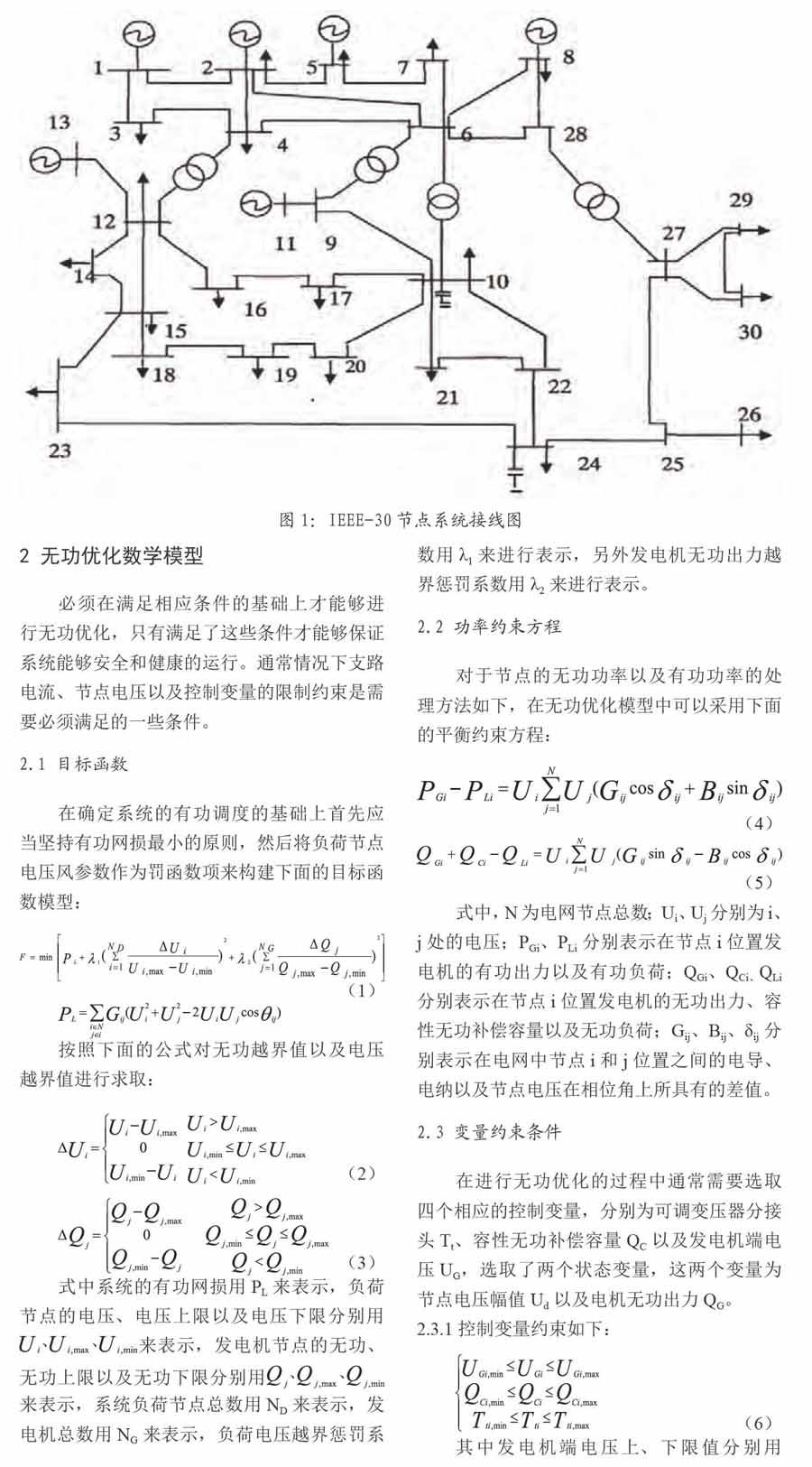
采用本文中所介紹的填充函數-粒子群算法對IEEE-30節點系統進行有效的優化，其中具體的參數接線圖以及系統接線圖如圖1所示。

在IEEE30節點系統總共具有四十余條支路、6個發電機節點、二十余個負荷節點、4條變比可調的變壓器支路以及3組相互并聯的電容器。6臺發電機中的節點1可以當做平衡節點，另外的五個發電機節點可以當做P-V節點。

在初始條件下將發電機的端電壓設置為1.0，將變壓器的變比設置為1.0，將無功補償量設置為0，經過潮流計算得到，U25=0.9425，U29=0.9392，U30=0.9276，沒有無功發電功率越限，并得到=2.9102，=0.9787，所以系統初始的網損=0.0762。

5 優化結果

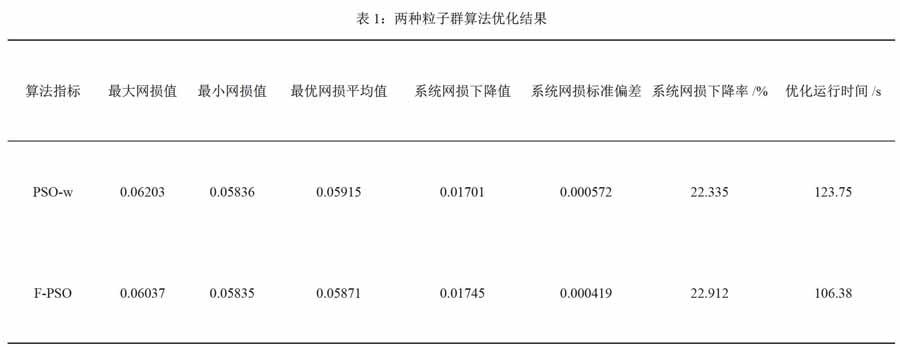
采用下面的方法對帶慣性權重的粒子群算法（PSO-w）中的參數進行優化，具體的優化流程如下：首先確定加速因子c1=c2=2，然后將慣性權重w減少，減少的依據要充分的參考具體的迭代次數。同時減少收縮擴張系數，按照線性的方式持續減小。對IEEE3O節點系統節點來說，粒子數選取50較為合適。系數=10，=5，兩種算法最大迭代次數取200，分別迭代次數運行30次，表1給出了優化后的數據統計結果。

從表1可以看出，PSO-w和F-PSO算法網損分別下降0.01701、0.01745，下降率分別為22.335%和22.912%，具有更加小的偏差，這有效的說明了說明該算法收斂穩定性非常好，具有一定的優越性。

6 結語

通過無功優化能夠在有效保證電力系統的安全性和穩定性的基礎上保證經濟運行的穩定，本文多采用的優化算法是一種比較智能的優化方法，能夠有效的解決傳統優化算法中存在的不足，為后續無功優化的研究提供豐富的理論和實踐參考。

參考文獻

[1]邱曉燕，張子健，李興源 .基于改進遺傳內點算法的電網多目標無功優化[J].電網技術，2012，33（13）：27-31.

[2]Kennedy J and Eberhart R C.Particle swarm optimization [C].In IEEE. Proceedings of IEEE International Conference on Neural Networks. Piscataway：IEEE，2011.67-69

[3]Shi Y and Eberhart R C.A modified particle swarm optimizer [C].In IEEE. Proceedings of the IEEE International Conference on Evolutionary Computation （CEC 1998）. Anchorage：IEEE，2013.69-73

[4]李博，魯殿軍，全局最優化問題的一個無參數的填充函數算法[J].數學雜志，2014，4（34）：773-778.

作者簡介

邱厚明（1990-），男，江西省上饒市人。上海電機學院碩士。主要研究方向為電力系統及其自動化

張向鋒（1977-），女，河南省孟津人。博士學位。現為上海電機學院碩士生導師、副教授。主要研究方向為智能控制。

作者單位

上海電機學院 上海市閔行區 201100