基于動力學模型的旋翼動平衡故障仿真及診斷

高軍龍，胡國才，吳靖

（海軍航空工程學院a.研究生管理大隊；b.飛行器工程系，山東煙臺264001）

基于動力學模型的旋翼動平衡故障仿真及診斷

高軍龍a，胡國才b，吳靖b

（海軍航空工程學院a.研究生管理大隊；b.飛行器工程系，山東煙臺264001）

旋翼槳葉質量不平衡造成旋翼動不平衡，從而引起直升機振動。針對旋翼動不平衡故障，建立直升機動力學模型，對槳葉質量不平衡進行故障仿真及分析，建立質量不平衡故障與調整配重的對應關系；進而提出一種BP神經網絡和遺傳算法結合的旋翼調整方法，建立輸入參數與槳葉配重之間的模型，將四片槳葉的揮舞角和機體橫滾、俯仰2個方向的加速度值及相位作為網絡輸入，通過學習訓練，根據輸入數據預測調整配重，從而減小直升機振動，解決旋翼動不平衡問題。

動平衡；BP神經網絡；遺傳算法；優化

旋翼作為直升機一個主要振源，其槳葉質量不平衡和氣動不平衡是引起機體振動加劇的常見原因。為了降低直升機振動，確保飛行安全，要定期對旋翼系統進行維護，不論什么故障引起的旋翼旋轉頻率（1Ω）［1］振動超標或槳尖脫錐，都是通過調整每片槳葉的小拉桿、槳轂配重、后緣調整片，使得槳尖同錐或振動減小到允許水平，從而確保機組人員和乘客的舒適性。

由于旋翼系統機械故障往往會導致嚴重的直升機飛行安全事故，因而國內外眾多學者對旋翼系統故障開展了大量的研究。主要的研究方法有：①基于直升機動力學模型的理論研究，可以任意設置故障；②通過人為設置進行模型旋翼的風洞試驗，根據故障與測量值之間的關系，建立故障診斷模型，開展故障識別；③通過直升機飛行測試獲得故障信息，但是考慮到安全性，一般不能隨意設置故障。文獻［2］基于動力學模型進行旋翼故障仿真與辨識，建立了帶外伸量的鉸接式旋翼模型，忽略槳葉的彈性變形，通過離散傅里葉變換矩陣，建立旋翼調整參數與機身振動值的對應關系，運用貝葉斯最小二乘法進行動不平衡與氣動不平衡的綜合調整；文獻［3］針對SH-60直升機建立了其動力學模型，采用彈性槳葉，前飛時采用自由尾跡非定常氣動模型，懸停時采用均勻入流氣動模型，針對旋翼設置不同的故障，通過對槳葉揮舞、擺振、扭轉及旋翼軸處載荷、扭矩等信號進行有限元［4］分析，得出每個故障相應的典型信號特征；文獻［5］在文獻［3］的基礎上，用故障仿真的數據對BP網絡進行訓練，實現對故障類型的診斷；文獻［6-7］中擴充了故障類型并仿真了復合故障，仿真結果表明BP網絡診斷復合故障仍然有效；文獻［8-9］建立了旋翼調整參數與直升機振動信號［10-12］之間的神經網絡模型，通過少量實測飛行數據訓練該模型，分別利用改進的遺傳算法和粒子群優化算法進行尋優，獲得當直升機振動最小時的槳葉調整量。

旋翼動不平衡主要表現為與旋翼旋轉頻率相關的不平衡載荷引起的直升機低頻振動，因而可采用文獻［13］所建立的旋翼/機體耦合動力學模型為基礎，設置旋翼慣性、氣動、剛度及阻尼等各種類型的故障［14］，對動力學模型進行仿真，獲得旋翼槳尖軌跡及機體振動響應與故障的映射關系。由于神經網絡具有很強的非線性映射能力，很容易實現槳葉調整參數和直升機振動信號之間的映射，因而本文采用基于BP神經網絡的旋翼調整方法，根據槳葉揮舞角和機體俯仰、橫滾加速度值及相位，利用BP神經網絡和遺傳算法的優化學習和調整技術，完成旋翼的動平衡調整。

1　直升機旋翼故障動力學模型

文獻［13］基于無故障旋翼建立了旋翼/機體耦合動力學模型。該模型適用于帶彈性軸承的鉸接式旋翼，也適用于變形主要發生在根部柔性元件的無鉸式及無軸承式旋翼，計入揮舞/擺振的結構耦合，直升機旋翼及機體的物理模型及坐標系如圖1所示。

旋翼出現的故障有：慣性類故障，如槳葉吸潮、丟失配重等；氣動類故障，如槳葉初始安裝角不等、調整片角度不同等；剛度類故障，如操縱線系剛度不同、變距拉桿關節軸承磨損等；阻尼類故障，如各槳葉減擺器阻尼不相同、水平鉸摩擦力矩不同等。所出現的故障都可以通過改變相應參數進行故障模擬。其中，質量不平衡不僅引起直升機振動，且引起氣動不平衡［15］，本文重點對旋翼質量不平衡進行數值故障模擬。

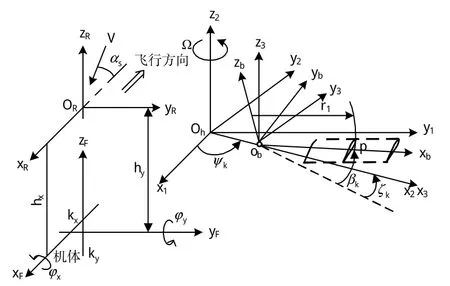
圖1　物理模型及坐標系Fig.1 Physical model and coordinate system

假設第k片槳葉出現質量不平衡，缺失質量m0，故障位置為r0，其第k片槳葉對揮舞-擺振鉸慣性矩、靜矩變為：

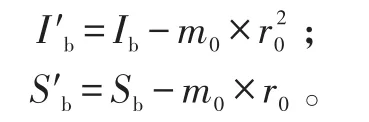
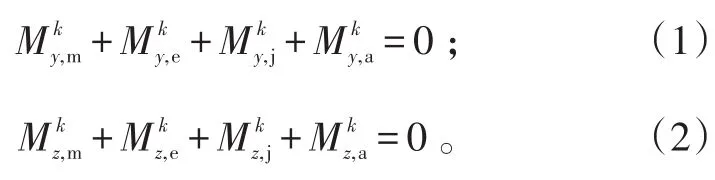
單片槳葉對機體運動瞬心作用的力矩有：槳葉慣性力及氣動力在揮舞和擺振鉸處的合力對機體作用的力矩，槳葉根部彈簧對機體作用的力矩。若第k片槳葉作用于機體的滾轉和俯仰力矩分別為，機體的滾轉及俯仰角位移分別為φx及φy，由機體運動瞬心的力矩平衡得到繞機體滾轉、俯仰軸的運動方程為：

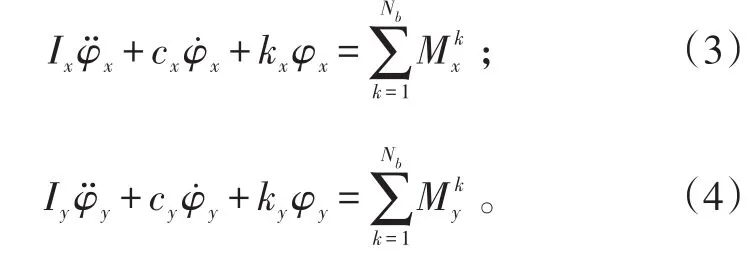
式（3）、（4）中：Ix、cx、kx為機體對滾轉軸的慣性矩、阻尼系數及約束剛度；Iy、cy、ky為機體對俯仰軸的慣性矩、阻尼系數及約束剛度。

這樣，該故障槳葉慣性力矩的改變，也會造成機體狀態的改變。

解決該故障需要在相應槳根與外伸量結合處增加配重，該配重質量為m′0，外伸量為e，會產生離心力m′0Ω2e，對機體產生橫滾、俯仰力矩為m′0Ω2eHsinψ、-m′0Ω2eHcosψ，ψ為故障槳葉的方位角，該力矩加入式（3）、（4）中。

用擴展的Pitt-Peters動力入流模型描述非定常氣動力的作用，動力入流方程為：

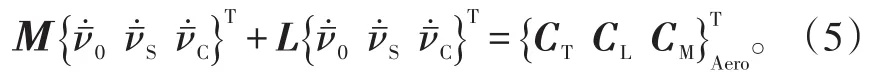
式（5）中：Μ、L分別為顯在空氣質量矩陣及入流的增益矩陣；CT、CL及CM分別表示旋翼總的氣動升力、對槳轂中心的氣動滾轉力矩及氣動俯仰力矩。

所有槳葉的揮舞、擺振運動方程與機體及入流方程聯立起來組成旋翼/機體耦合系統的運動方程組。

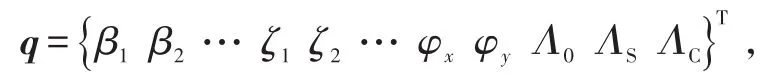
將運動方程組寫成簡潔的形式為：

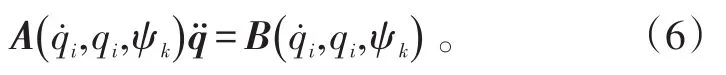
式（6）中：A為（2N+5）×（2N+5）的矩陣，N為槳葉片數；B為（2N+5）×1的向量。

2　旋翼動不平衡仿真

根據部位實際維護情況，如果直升機旋翼系統出現動不平衡及不共錐的情況，要先進行地面測試調整，再進行空中測試調整。下面進行地面旋翼數值故障模擬。

2.1故障設置

所用模型為無鉸旋翼模型，額定轉速為1 000 r/min，總距為6°，槳葉片數為4片，黑色槳葉（B）為基準槳葉，其余3片分別為紅（C）、綠（D）和藍（E）。設置5組故障，其中第4片槳葉（藍）不設置故障，槳葉缺失質量為槳葉總質量（G）的1%、2%和5%；R為槳葉半徑，故障位置為0.2R、0.5R、0.8R，故障設置如表1所示。

表1　故障設置Tab.1 Faults setting

2.2結果分析

第1組故障仿真結果如圖2、3所示，圖2為4片槳葉穩定時的揮舞值，圖3為機體穩定時的橫滾（J）、俯仰（K）值；表2前5組為故障仿真數據，第6組所得數據是在第5組故障的基礎上，在綠色槳根處增加配重m′1=0.039 3GR e后的仿真結果。因為實際維護過程中，提取機體振動值都是用加速度傳感器，衡量振動標準的單位為IPS［16］，故表中橫滾、俯仰值為橫滾、俯仰角加速度（弧度）除以旋翼轉速。

根據表2得知，當某片槳葉出現質量不平衡時，也會影響其余3片槳葉的共錐度，旋翼/機體發生耦合，其故障槳葉揮舞角極值最大；由第1組數據可以看出，第1片槳葉出現故障時，機體橫滾、俯仰峰值分別為0.041 7、0.014 0，相位為89°、180°，其他槳葉單獨出現故障時，相位依次向后推遲90°；故障質量相同時，隨著故障位置的增加，橫滾、俯仰峰值成正比增加，槳葉共錐度發生變化；當故障位置相同，隨著故障質量的增加，橫滾、俯仰峰值成正比增加，槳葉共錐度發生變化；在故障槳葉外伸量與槳根結合處增加一定配重后，機體俯仰、橫滾值在1Ω下達到允許值［17］。

圖2　槳葉揮舞值Fig.2 Blade flapping value

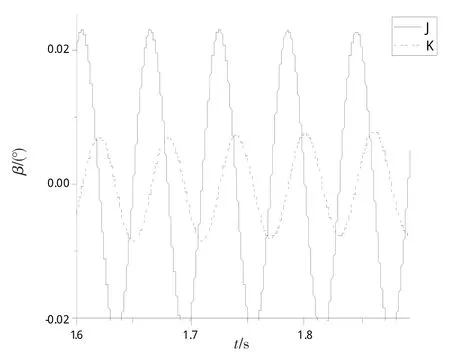
圖3　機體橫滾、俯仰Fig.3 Roll and pitch of fuselage

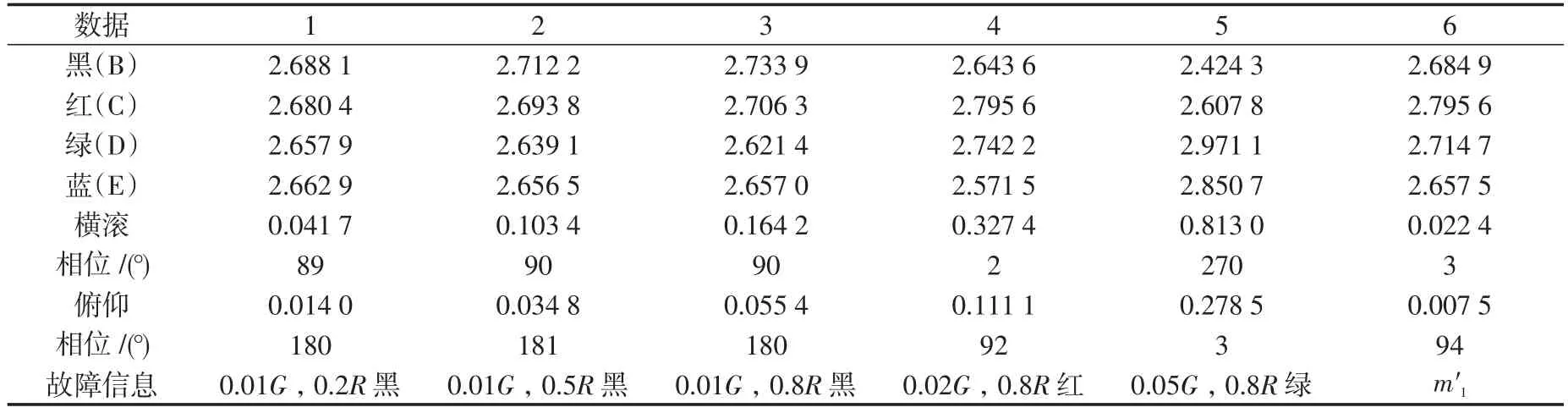
表2　仿真數據Tab.2 Simulation data

3　故障診斷

3.1旋翼動平衡調整機理

直升機旋翼錐體與動平衡調整的目的是為了使直升機3個方向的一階振動降到符合要求的水平，使機組人員和乘客的舒適度最佳。本文針對的是單一質量故障，所以當旋翼出現動不平衡后，通過配重塊來達到平衡的目的。由于槳葉揮舞值和機體振動與旋翼調整參數之間具有非線性關系，因此利用神經網絡建立調節參數和槳葉揮舞值、機體俯仰橫滾一階振動之間的傳遞函數，根據旋翼共錐度和機體振動值預測旋翼調整參數，具體原理見圖4。

通過提取槳葉揮舞值和機體俯仰、橫滾振動幅值及其相位，輸入到神經網絡中，經過神經網絡和遺傳優化算法的優化分析得出一個合適的槳葉配重調整量，以此調節相應的參數實現對旋翼質量不平衡引起的振動和錐體不共錐進行控制，減小直升機的振動。

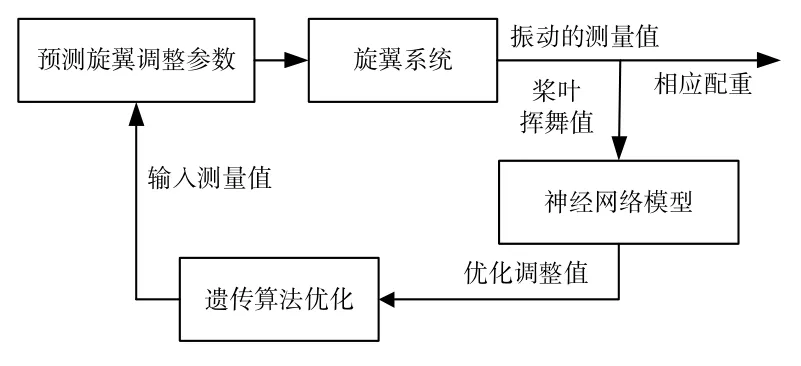
圖4　旋翼動平衡調整原理圖Fig.4 Schematic of rotor dynamic balance adjustment

3.2旋翼動平衡調整神經網絡建模

根據旋翼故障數值模擬，可仿真出大量的故障數據，而BP神經網絡在訓練樣本多的情況下精度很好。本文采用BP神經網絡建立旋翼調整模型如圖5所示。圖中，神經網絡的輸入為各槳葉揮舞值和機體俯仰、橫滾值及相位（用Xi表示，i=1，2，…，8），神經網絡的輸出為需要在槳根處所加的配重量（Y1為配重大小，Y2為增加配重的槳葉）。由于旋翼共有4片槳葉，因而可確定神經網絡輸入層神經元為8個，輸出層神經元個數為2個。

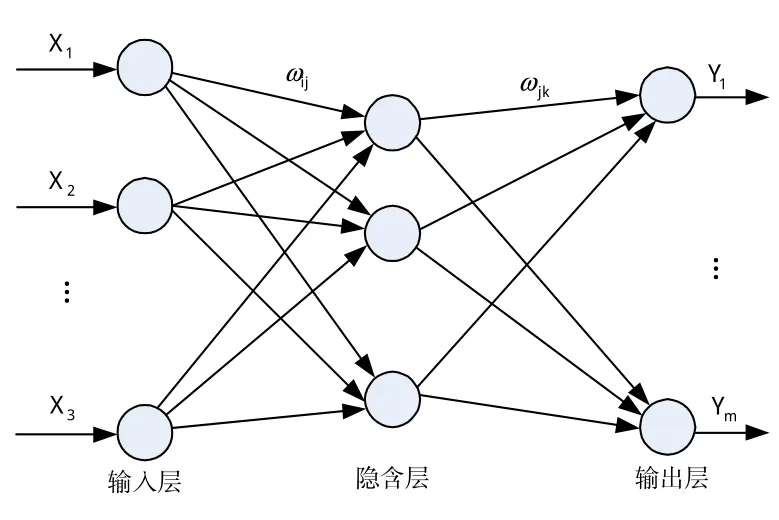
圖5　旋翼系統的BP模型Fig.5 BP model of rotor system

3.3AGA優化BP神經網絡

遺傳算法優化BP神經網絡算法流程如圖6所示。遺傳算法優化BP神經網絡分為BP神經網絡結構確定、遺傳算法優化和BP神經網絡預測3個部分。其中，BP神經網絡結構確定部分根據擬合函數輸入輸出參數個數確定BP神經網絡結構，進而確定遺傳算法個體的長度。遺傳算法優化使用遺傳算法優化BP神經網絡的權值和閾值，使優化后的BP神經網絡能夠更好地預測函數輸出。種群中的每個個體都包含了一個網絡所有權值和閾值，個體通過適應度函數計算個體適應度值，遺傳算法通過選擇、交叉和變異操作找到最優適應度值對應個體。BP神經網絡預測用遺傳算法得到最優個體對網絡初始權值和閾值賦值，網絡經訓練后預測函數輸出。遺傳算法優化BP神經網絡的要素包括種族初始化、適應度函數、選擇操作、交叉操作和變異操作。

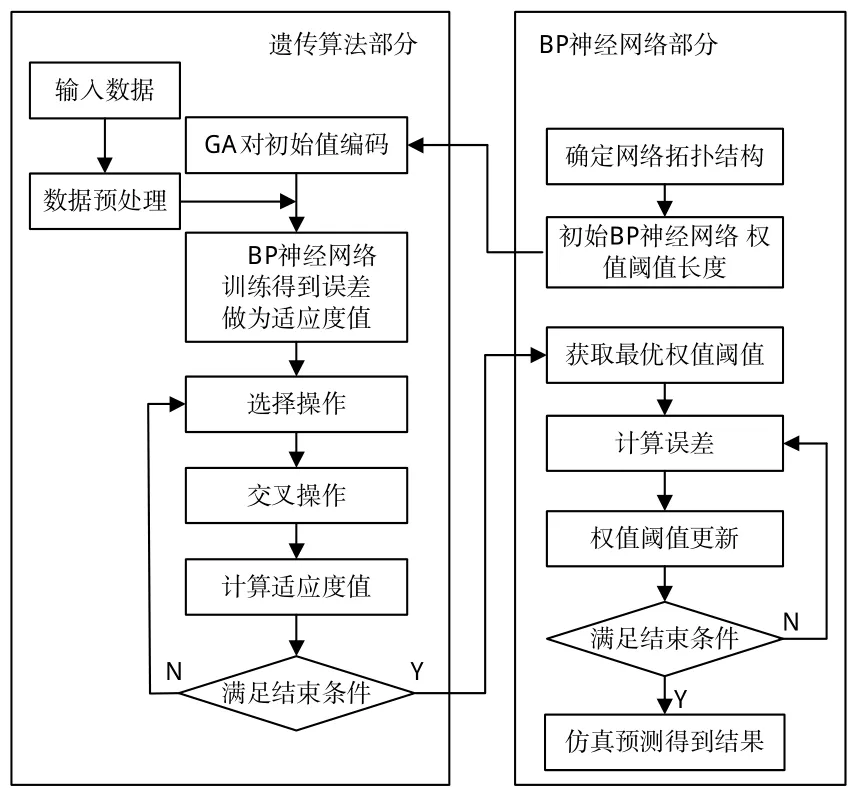
圖6　算法流程Fig.6 Algorithm flowchart

1）種族初始化。個體編碼方法為實數編碼，每個個體均為一實數串，由輸入層與隱含層連接權值、隱含層閾值、隱含層與輸出層連接權值以及輸出層閾值4部分組成。個體包含了神經網絡全部權值和閾值，在網絡結構已知的情況下，就可以構成一個結構、權值、閾值確定的神經網絡。

2）適應度函數。根據個體得到BP神經網絡的初始權值和閾值，用訓練數據訓練BP神經網絡后預測系統輸出，把預測輸出和期望輸出之間的誤差絕對值和E作為個體適應度值F，計算公式為：

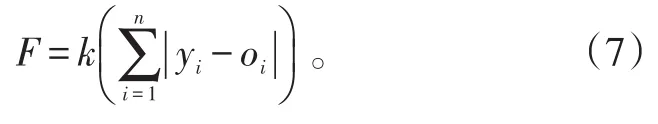
式（7）中：n網絡輸出節點數；yi為BP神經網絡第i個節點的期望輸出；oi為第i個節點的預測輸出；k為系數。

3）選擇操作。遺傳算法選擇操作有輪盤賭法、錦標賽法等多種方法，本案例選擇輪盤賭法，即基于適應度比例的策略，每個個體i的選擇概率pi為：

式（8）、（9）中：Fi為個體i適應度值，由于適應度值越小越好，所以在個體選擇前對適應度值求倒數；k為系數；N為種群個體數目。

4）交叉操作。由于個體采用實數編碼，所以交叉操作方法采用實數交叉法，第k個染色體ak和第l個染色體al在j的交叉操作方法如下：

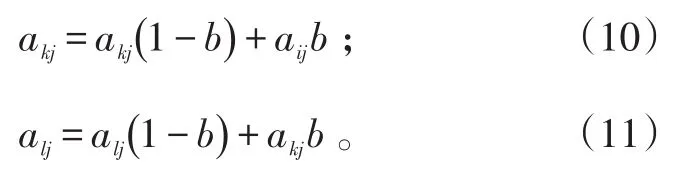
式（10）、（11）中，b是［0，1］間的隨機數。

5）變異操作。選取第i個個體的第j個基因aij進行變異，變異操作方法如下：

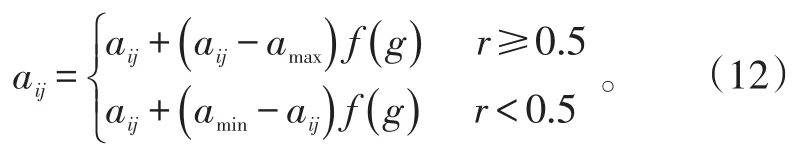
式（12）中：amax為基因aij的上界；amin為基因aij的下界；；r2為一個隨機數；g為當前迭代次數；Gmax是最大進化次數；r為［0，1］間的隨機數。

3.4仿真數據試驗測試

在仿真模型的基礎上，設置單一的槳葉質量故障，隨機生成故障質量，每片槳葉故障數據為1 000組，共隨機生成4 000組仿真數據，每組數據包括機體的橫滾、俯仰峰值及其相位和四片槳葉的揮舞值。利用遺傳算法優化的BP神經網絡對其中隨機選取的3 800組數據進行學習訓練，200組作為測試數據。其中，故障質量范圍為槳葉質量的±1%以內，槳葉揮舞值和機體俯仰、橫滾值及其相位為輸入層共有8個節點，隱含層有16個節點，輸出層為槳根處的調整配重，共有2個節點；選擇種群規模為20個，進化代數n=20次，交叉概率為0.4，變異概率為0.2。圖7、8是根據200組測試數據所得調整配重的大小及其相位的相對誤差（百分比）預測圖。

由圖7、8可知，預測調整配重的質量相對誤差全部小于4%，而相對誤差大于1%的只有4組數據；由于相位信息特征比較明顯，預測結果全部正確。

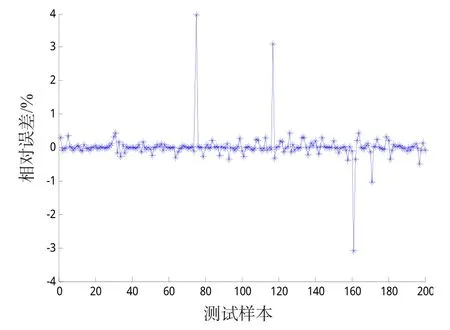
圖7　質量誤差Fig.7 Quality error

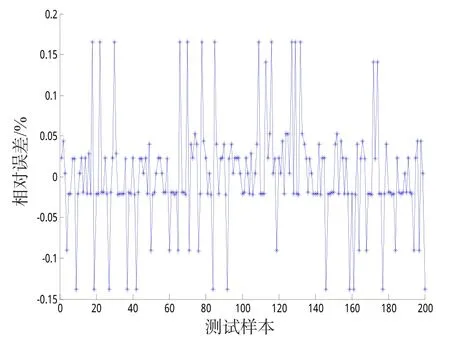
圖8　相位誤差Fig.8 Phase error

4　結論

通過建立動力學建模，對槳葉質量不平衡進行數值故障模擬，發現了槳葉質量不平衡時與機體振動的聯系，并會引起錐體不共錐，建立了質量不平衡故障與調整配重的對應關系。根據旋翼模型的非線性特點，采用BP網絡建立旋翼調整模型，并應用AGA進行優化，獲得了槳葉質量不平衡時的調整配重。仿真數據和分析結果表明：采用BP網絡與遺傳算法相結合的方法能夠正確診斷槳葉質量不平衡故障。

［1］周秋峰.直升機旋翼動平衡優化研究［D］.南京：南京航空航天大學，2013. ZHOU QIUFENG.Resarch on optimization of helicopter rotor dynamic balance［D］.Nanjing：Nanjing University ofAeronautics andAstronautics，2013.（in Chinese）

［2］ERIC BECHHOEFER，AUSTIN FANG，EPHRAHIM GARCIA.Rotor track and balance improvement［C］//Annual Conference of Prognostics and Heath Management Society 2013.Montreal：American Helicopter Society，2013：1-9.

［3］GANGULI R，CHOPRA I，HAAS D J.Formulation of a helicopter rotor system damage detection methodology［C］//36thStructures，Structural Dynamics and Material Conference.New Orleans：AIAA，1996：302-312.

［4］GANGULI R，CHOPRA I，HAAS D J.Helicopter rotorsystem damage detection［C］//Proceedings of the Aeromechanics Meeting of the American Helicopter Society.Fairfield County，Connecticut，1995：102-110.

［5］GANGULI R，CHOPRA I，HAAS D J.Detection of heli-copter rotor system simulated faults using neural networks［J］.Journal of the American Helicopter Society，1997，42（2）：161-171.

［6］GANGULI R，CHOPRA I，HAAS D J.A physical based model for rotor system health monitoring［C］//European Rotorcraft Forum.Brighton.United Kingdom.1996：98-1-98-22.

［7］GANGULI R，CHOPRA I，HAAS D J.Helicopter rotor system health monitoring using numerical simulation and neural networks［C］//Annual Conference of Prognostics and Heath Management Society 1997.Virginia Beach，VA：American Helicopter Society，1997：1285-1296.

［8］劉紅梅，王少萍，歐陽平超.基于GRNN網絡和遺傳算法的旋翼動平衡調整［J］.北京航空航天大學學報，2008，34（5）：507-511. LIU HONGMEI，WANG SHAOPING，OUYANG PINGCHAO.Helicopter rotor smoothing based on GRNN neural network and genetic algorithm［J］.Joumal of Beijing University of Aeronautics and Astronautics，2008，34（5）：507-511.（in Chinese）

［9］劉紅梅，呂琛，歐陽平超.粒子群優化在直升機旋翼動平衡調整中的應用［J］.北京航空航天大學學報，2011，37（3）：283-288. LIU HONGMEI，LV CHEN，OUYANG PINGCHAO.Helicopter rotor tuning based on neural network and particle swarm optimizaton［J］.Joumal of Beijing University of Aeronautics and Astronautics，2011，37（3）：283-288.（in Chinese）

［10］高亞東，張曾锠.用機體振動信號振動旋翼不平衡故障診斷的理論基礎［J］.振動、測試與診斷，2003，23（4）：279-282. GAO YADONG，ZHANG ZENGCHANG.A theoretical basis for diagnosis of helicopter rotor imbalance fault using only information from fuselage vibrations［J］.Journal of Vibration，Measurement&Diagnosis，2003，23（4）：279-282.（in Chinese）

［11］高亞東，鄧升平.基于支持向量機的直升機旋翼不平衡故障分類研究［J］.南京航空航天大學學報，2011，43（30）：435-438. GAO YADONG，DENG SHENGPING.Unbalance fault identification of helicopter rotor using support vector machine［J］.Journal of Nanjing University of Aeronautics& Astronautics，2011，43（30）：435-438.（in Chinese）

［12］高亞東，張曾锠.直升機旋翼不平衡故障診斷試驗研究［J］.振動、測試與診斷，2009，29（2）：435-438. GAO YADONG，ZHANG ZENGCHANG.Experimental study on unbalance fault diagnosis of helicopter rotor［J］. Journal of Vibration，Measurement&Diagnosis，2009，29（2）：435-438.（in Chinese）

［13］胡國才.減擺器非線性特性及其對直升機旋翼/機體耦合動穩定性影響研究［D］.北京：北京航空航天大學，2003. HU GUOCAI.Nonlinear characteristic of blade lag dampers and its effect on helicopter rotor/airframe coupled dynamic stability［D］.Beijing：Beihang University，2003.（in Chinese）

［14］RANJAN GANGULI，INDERJIT CHOPRA，DAVID J HAAS.Simulation of helicopter rotor-system structural damage，blade mistracking，friction，and freeplay［J］.Journal ofAircraft，1998，35（4）：591-597.

［15］鄧升平.旋翼不平衡故障試驗及診斷方法研究［D］.南京：南京航空航天大學，2010. DENG SHENGPING.Research on helicopter rotor imbalance fault experiment and diagnosis method［D］.Nanjing：Nanjing University of Aeronautics and Astronautics，2013.（in Chinese）

［16］王強，蔣安民.基于Model2020的直升機旋翼錐體及動平衡技術研究［J］.航空維修與工程，2009（6）：62-64. WANG QIANG，JIANG ANMIN.The research of track and dynamic balance for helicopter rotor based on the model 2020［J］.Aviation Maintenance&Engineering，2009（6）：62-64.（in Chinese）

［17］鄧景輝，方永紅.直升機旋翼錐體與平衡調整方法研究［J］.直升機技術，2004（1）：9-13. DENG JINGHUI，FANG YONGHONG.A research on tracking and balance tuning for helicopter rotor［J］.Helicopter Technique，2004（1）：9-13.（in Chinese）

Fault Simulation and Diagnosis of Helicopter Rotor Dynamic Balance Based on Dynamic Model

GAO Junlonga，HU Guocaib，WU Jingb
（Naval Aeronautical and Astronautical University a.Graduate Students'Brigade；b.Department of Airborne Vehicle Engineering，Yantai Shandong 264001，China）

Rotor mass unbanlance leads to dynamic unbalance of rotor-system，thus it causes helicopter vibration.According to the faults of rotor dynamic unbalance，the dynamics model of helicopter was constructed to simulate and analyze mass unbalance of blade，and the relation was found out between the mass unbalance and adjusting weight.And then a methodology of rotor adjustment was presented based on the combination of BP neural network and genetic algorithm，and a model was established between the inputs and weights that included the flapping angles of 4 blades and the accelerations and phases of body roll and pitch.The model would predict the adjustment weights throught learning and training，so as to reduce the vibration of the helicopter，and solve the problem of rotor unbalance.

dynamic balance；BP（back propagation）neural network；genetic algorithm；optimization

V211.73

A

1673-1522（2016）03-0317-06DOI:10.7682/j.issn.1673-1522.2016.03.004

2016-02-24；

2016-04-15

高軍龍（1988-），男，碩士生；胡國才（1964-）男，教授，博士，博導。