MIMO 仿射型非線性系統的滑模切換極值搜索控制

張雷，胡云安，李靜

（海軍航空工程學院a.控制工程系；b.七系，山東煙臺264001）

MIMO 仿射型非線性系統的滑模切換極值搜索控制

張雷a，胡云安a，李靜b

（海軍航空工程學院a.控制工程系；b.七系，山東煙臺264001）

針對MIMO仿射型非線性系統設計了一種基于分數階積分的滑模切換極值搜索控制方法，將系統分解為若干個子系統，對每個子系統采用輸出跟蹤誤差以及該誤差函數的分數階積分值構造切換函數，構造滑模切換極值搜索控制律，證明了方法的穩定性。對比已有的方法進行仿真分析，驗證了方法具有較好性能。

仿射型非線性系統；極值搜索；切換函數；分數階

極值搜索方法自1954年由Tsien提出，就被確認為是自適應控制方法的一種［1］。其中，滑模極值搜索方法可以在不知曉參考函數梯度的情況下，運用滑模控制，使得控制對象輸出跟蹤單調遞減從而使參考函數取得最優值［2］。2000年，Haskara等通過在系統反饋中引入一個自由參數，利用雙時間軸滑模控制完成了系統性能的最優化［3］。2002年，Yu Hai等在以往滑模極值搜索方法研究的基礎上，提出了采用鋸齒波周期信號設計的方法，此法也能較好地實現極值搜索的過程［4］。滑模極值搜索方法陸續地運用到線性二次型動態對策問題的求解和汽車剎車系統等實際系統［5-7］。近年來，隨著自適應控制理論的巨大發展，滑模極值搜索方法再次成為控制界研究的熱點。文獻［8］針對非線性極值搜索系統提出了分數階極值搜索控制方法，并應用于光伏系統的實際控制中；文獻［9］針對SISO仿射非線性系統提出了滑模切換極值搜索方法，結合迭代法則設計了切換函數和控制律；文獻［10］針對非仿射非線性系統提出了基于分數階PI滑模面的滑模極值搜索控制方法；文獻［11］提出了SISO非仿射非線性系統的分數階滑模極值搜索方法；文獻［12］針對MIMO仿射非線性極值搜索系統提出了輸出反饋滑模控制方法。多種不同類型極值搜索控制方法［13-18］一定程度上解決了一些非線性極值搜索系統的控制問題，為以后的針對性研究提供了理論參考。

本文在文獻［12］方法的基礎上設計了基于分數階積分的滑模切換極值搜索控制方法。該方法利用常值函數作為輸出量的參考跟蹤信號，采用輸出跟蹤誤差以及該誤差函數的分數階積分值構造切換函數，設計得到滑模切換極值搜索控制律。本文方法不僅可以實現對被控對象的極值控制，而且準確性較好。

1　問題闡述

考慮如下MIMO仿射型非線性系統

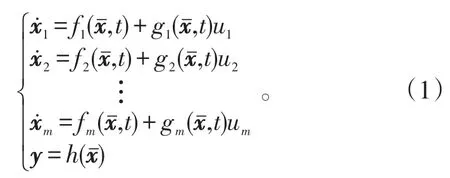
假設2：在系統（1）中，光滑函數gi，t）存在非零下界，即，其中，Gi為下界值，1≤i≤m。

控制目標：針對系統（1），設計滑模切換極值搜索控制律，使得閉環系統穩定且系統輸出y收斂至對應的極大值y?的有界鄰域內。

經分解得到系統（2）屬于原始系統（1）的子系統，具有輸出極大值。其滿足假設2的條件，由假設2可知系統（2）中的存在非零下界，即，1≤i≤m。

同樣也滿足對于給定的常數Δi＞0（Δi＜Δ），總存在另一個常數，使得成立。其中，為關于極值點的Δi鄰域，且。

假設4：存在已知的K∞函數和滿足局部Lipschitz條件的ηi和一個在上連續，在t上分段連續，且上界已知的非負函數ψi（，t），使得成立。

根據系統（1）的既定控制目標，轉換得到新系統控制目標：設計滑模切換極值搜索控制律，使閉環系統（2）漸近穩定，且該系統的狀態量和輸出量均一致范數有界，輸出量收斂至極大值的有界鄰域內。

引入分數階積分［10］的定義為

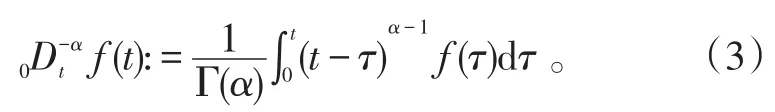
式（3）中：α＞0；f（t）是任意的積分函數；Γ（·）是Gamma函數。

分數階Caputo微分［10］的定義為

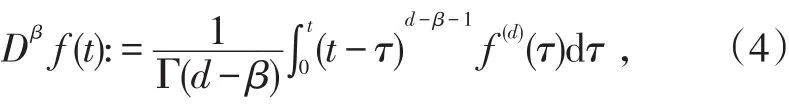
式中，d-1＜β＜d。

引理1［10］：分數階為β∈C且Re（β）＞0的分數階積分是關于Lp（a，b）有界的，其中，1＜p≤+∞，

對于滑模切換極值搜索控制方法而言，采用分數階積分可以獲得更好的控制效果，使得系統輸出y更準確的收斂至對應的極大值y?的有界鄰域內。

2　滑模切換極值搜索控制方法設計

式中，yr＞0為非負常數的跟蹤參考信號。

針對系統（2），設計控制律ui為

式（6）中：λ0＞0為設計常數；ρi（1≤i≤m）為調制函數，為了弱化符號函數而引起的切換過程的影響，采用雙曲正切函數tanh（·）代替符號函數。

設計切換函數σ（t）為

式（7）中：-1＜q＜0；λ1＞0和λ2＞0為設計常數。

對σ（t）求取一階微分，并代入式（7），可得：

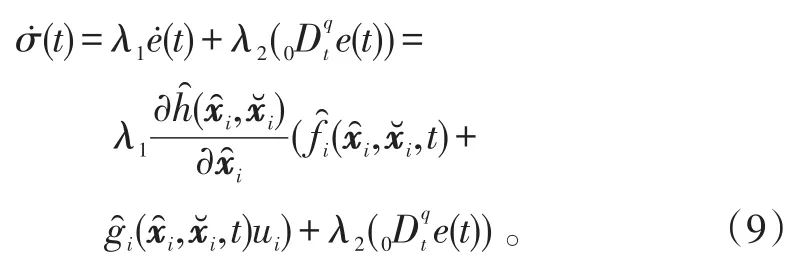
設計一種調制函數保證系統（2）中的信號向量不會在有限時間內發散，同時保證滑動模式σ（t）=kλ0的存在。調節向量ρi設計滿足：

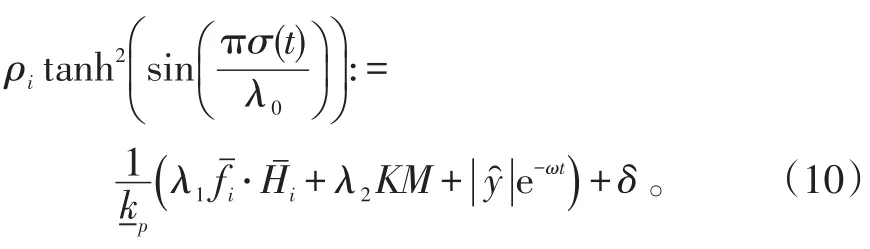
式（10）中：ω＞0為衰減指數；δ＞0為任意小常數。

3　控制系統的穩定性分析

針對系統（2），當采取如式（6）、（7）和式（10）所示的分數階滑模切換極值搜索控制律ui時，構成的閉環系統框圖如圖1所示。

圖1　閉環控制系統框圖Fig.1 Frame of closed-loop control system

定理1：針對系統（2），采用分數階滑模切換極值搜索控制律ui如式（6）、（7）和式（10）所示，則在有限時間內，系統狀態量、輸出量和切換函數信號σ都不會出現發散現象。

證明：首先，構造非負積分型函數S1（σ）和S2（σ）。不失一般性地，設計S1（σ）為

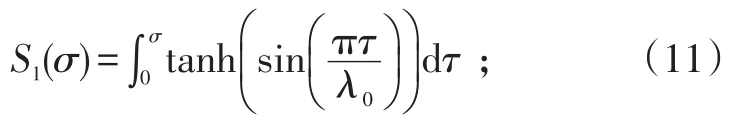
設計S2（σ）為

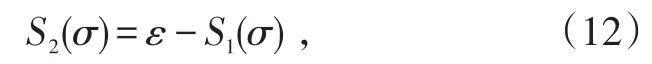
其中，ε是S1（σ）中的最大值。

對S1（σ）和S2（σ）分別求一階微分，代入式（9）、（10），通過可得當sgn（kpi）＜0時，

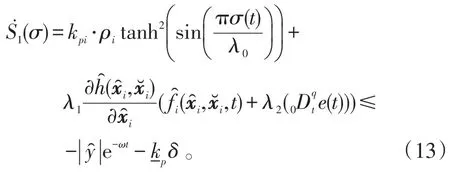
以此類推，可得sgn（kpi）＞0時，

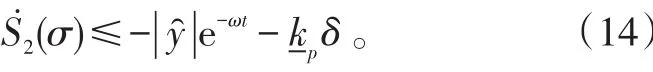
下面，證明系統（2）中的信號都不會出現發散現象。

采用反證法進行證明，首先假設在時刻t1∈［）0，∞時，函數σ會出現發散現象，則根據σ的定義式（7）可知，誤差e（t）和輸出量（t）都會出現發散現象。因此，假設存在時刻，使得在區間內，成立，其中δ1為任意小的正數。或者時成立。

由于假設當t≥t1時，切換函數σ已發生了發散現象，考慮到切換函數σ的連續性，存在時刻t3∈［t2，t1）和整數kσ，使得Σ（t3）=kσλ0。當kσ為偶數時，S1（σ（t3））=0。用S1（t）代替S1（σ（t）），用S2（t）代替S2（σ（t）），由此可知，對于任意的時刻t∈［t3，t1），S1（σ）=0或者S2（σ）=0，此時切換函數σ（t）=kσλ0是有界的。與前提假設“在時刻t1∈［0，∞）時，切換函數σ會出現發散現象”是矛盾的。因此，該假設不成立，即（t）和其他閉環信號在有限時間內都不會出現發散現象。

定義Lyapunov函數如下：

對式（15）求一階微分，并代入式（6）、（9）可得：

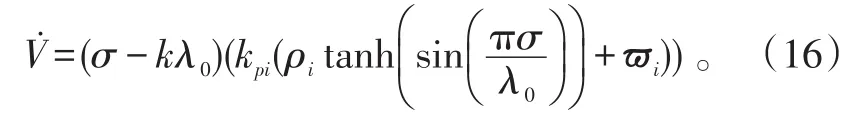
由切換函數σ的定義可知，當kpi＜0時，切換函數σ會運動至σ=kλ0，其中k為偶數，將式（9）、（10）代入式（16），可得當t≥ta時，存在：

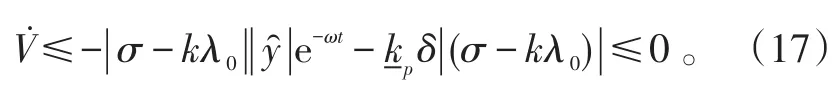
當kpi＞0時，切換函數σ也會運動至σ=kλ0，其中k為奇數，同理可得：

定理2：針對系統（2），滿足假設條件1～4，如果采用控制律如式（6）、（7）和式（10）所示，那么狀態量將在有限時間內全局收斂至鄰域內，并且對于足夠小的，輸出量在極大值附近的振蕩幅值是關于參數λ0的無窮小量，即，同時狀態量以及輸出量都是一致范數有界。

由定義式（7）可得

假設當時刻t=t1（t1＞t?）時，狀態量從鄰域內運動至其邊緣處。對于?t＞t1，存在：

設定t2（t2＞t1）為切換函數σ達到下一個滑模面的時刻，t3（t3＞t1）為切換函數σ第一次從鄰域外部再次返回到鄰域邊緣的時刻。

①如果t3＞t2，則可將時間分為兩個階段t∈［t1，t2）和。

根據式（9）和式（13），可得：

將式（19）與式（20）相減，可得：

②如果t2≥t3＞t?，分析輸出量從t1運動到t3的情況，由于此時切換函數σ不處于滑模面上，那么對于，輸出量的運動情況可以類比于①中的情況，因而，可知此時

證畢。

綜上所述，對于非線性極值搜索系統（1）中的第i（1≤i≤m）個極值搜索子系統（2），如果采用控制律如式（6）、（7）和式（10）所示時，狀態量可在有限時間內全局收斂至鄰域內時，即存在和。因此，當采取與定理2相類似的控制條件時，系統（1）的狀態量都能在有限時間內全局收斂至，根據假設3可知，此時狀態量處于鄰域DΔ內。

4　仿真分析

考慮一類求解納什均衡解問題，數學模型［12］為

分析模型可知，當x1=0和x2=0時，輸出量y1和 y2具有極大值=20和=15。

采用本文方法對比文獻［12］方法進行仿真對比驗證，采用本文方法時仿真參數選取為：q=-0.5、yr=20、λ0=0.05、λ1=0.1、λ2=0.1、ω=5、δ=0.1；采用文獻［12］方法時仿真參數選取為：q=0、kr=1、γ=0.1、β=2、δ=0.1、ε=0.02。當系統狀態量的初始條件分別為x1（0）=1和x2（0）=1.5時，得到的仿真結果分別如圖2～7所示。

圖2　狀態量x1的仿真結果Fig.2 Result of the statex1

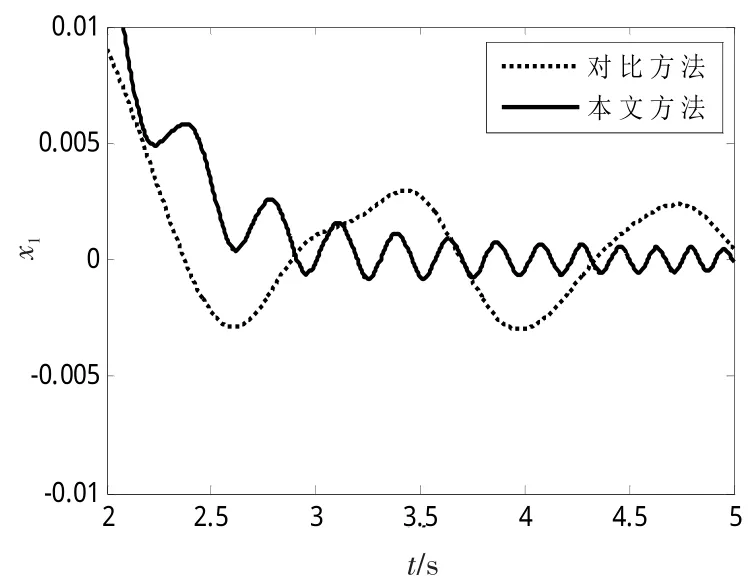
圖3　穩定狀態下x1的放大仿真結果Fig.3 Amplified result of the steady statex1

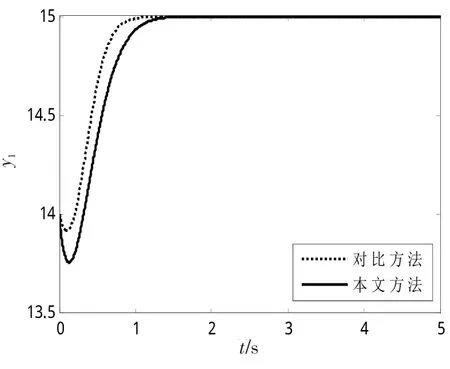
圖4　輸出量y1的仿真結果Fig.4 Result of the outputy1

圖5　狀態量x2的仿真結果Fig.5 Result of the statex2

圖6　穩定狀態下x2的放大仿真結果Fig.6 Amplified result of the steady statex2

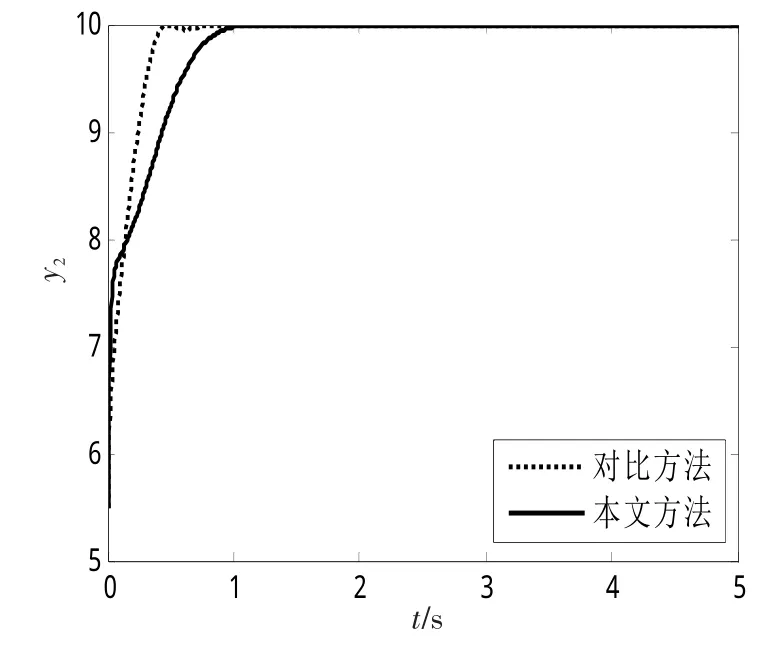
圖7　輸出量y2的仿真結果Fig.7 Result of the outputy2

對比圖2～7可知：采用本文的分數階滑模切換極值搜索方法進行仿真時，狀態量x1和x2能夠快速收斂至目標函數取極大值時對應的=0和=0的有界鄰域內，且當系統達到穩定狀態時，積分算子階次q選取為-0.5時系統狀態的振蕩比取q1=0時（即為積分階次為1的整數階）的系統狀態振蕩要小，即能夠取得更為準確的收斂效果；由圖4、7可知：目標函數y1和y2分別快速收斂至極大值=15和=10處。

5　結論

采用本文設計的分數階滑模切換極值搜索方法，該系統的狀態量、控制輸入和目標函數均一致有界，目標函數y收斂至極大值y?的有界鄰域內。且對于基于整數階積分的滑模切換極值搜索方法而言，采用分數階積分可以有效改善方法的準確性，取得更好的控制效果。

［1］左斌，李靜，胡云安.極值搜索算法研究及其應用［M］.北京：國防工業出版社，2014：9-10. ZUO BIN，LI JING，HU YUNAN.Research on extremum seeking algorithm and its application［M］.Beijing：National Defense Industry Press，2014：9-10.（in Chinese）

［2］KOROVIN S K，UTKIN V I.Using sliding modes in static optimization and nonlinear programming［J］.Automatica，1974，10（5）：525-532.

［3］HASKARA I，OZGUNER U，WINKELMAN J.Extremum control for optimal operating point determination and set point optimization via sliding modes.，journal dynamic systems［J］.Measurement and Control，2000，122（4）：719-724.

［4］YU H，OZGUNER U.Extremum-seeking control via sliding mode with periodic search signals［C］//Proceedings of the 41stIEEE International Conference on Decision and Control.Las Vegas，USA：IEEE，2002：323-328.

［5］DRAKUNOV S，OZGUNER U，DIX P，et al.ABS control using optimum search via sliding mode［J］.IEEE Transactions on Control Systems Technology，1995，3（1）：79-85.

［6］PAN Y D，ACARMAN T，OZGUNER U.Nash solution by extremum seeking control approach［C］//Proceedings of the 41stIEEE Conference on Decision and Control.Las Vegas，USA：IEEE，2002：329-334.

［7］PAN Y D，OZGUNER U.Sliding mode extremum seeking control for linear quadratic dynamic game［C］//Proceeding of the 2004 American Control Conference.Boston，USA：IEEE，2004：614-619.

［8］AMMAR NE?AIBIA，SAMIR LADACI，ABDELFATAH CHAREF，et al.Fractional order extremum seeking approach for maximum power point tracking of photovol-taic panels［J］.Frontiers in Energy，2015，9（1）：43-53.

［9］YIN CHUN，STARK BRANDON，ZHONG SHOUMING，et al.Global extremum seeking control with sliding modes for output-feedback global tracking of nonlinear systems［C］//Proceeding of the 51stConference on Decision and Control.Maui，Hawaii，USA：IEEE，2012：7113-7118.

［10］YIN CHUN，CHENG YUHUA，ZHONG SHOUMING，et al.Fractional-order sliding mode-extremum seeking control design with fractional-order PI sliding surface［C］// Proceeding of the 34thChinese Control Conference.2015. Hangzhou：IEEE，539-544.

［11］YIN CHUN，CHEN YANGQUAN，ZHONG SHOUMING.Fractional-order sliding mode based extremum seeking control of a class of nonlinear systems［J］.Automatica，2015，50：3173-3181.

［12］左斌，張雷，李靜.MIMO仿射型極值搜索系統的輸出反饋滑模控制［J/OL］.北京航空航天大學學報，http：// www.cnki.net/kcms/detail/11.2625.V.20150803.1423.008. html. ZUO BIN，ZHANG LEI，LI JING.Output-feedback sliding modecontrol for MIMO affine extremum seeking systems［J/OL］.Journal of Beijing University of Aeronautics andAstronautics，http：//www.cnki.net/kcms/detail/ 11.2625.V.20150803.1423.008.html.（in Chinese）

［13］KRSTIC M.Toward faster adaptation in extremum seeking control［C］//Proceeding of the 39thIEEE Conference on Decision and Control.Phoenix，USA：IEEE，1999：4766-4771.

［14］TAN Y，NESIC D，MAREELS I.On stability properties of a simple extremum seeking scheme［C］//Proceedings of the 45thIEEE Conference on Decision&Control.San Diego，USA：IEEE，2006：2807-2812.

［15］YE MAOJIAO，HU GUOQIANG.A robust extremum seeking scheme for dynamic systems with uncertainties and disturbances［J］.Automatica，2016，66：172-178.

［16］ARIYUR K B，KRSTIC M.Slope seeking：a generalization of extremum seeking［J］.International Journal of Adaptive Control Signal Processing，2004，18（1）：1-22.

［17］左斌，李靜.控制增益未知的多變量極值搜索系統神經網絡自適應協同控制［J］.控制理論與應用，2013，30（4）：405-416. ZUO BIN，LI JING.Neural network adaptive synergetic control for mulitvairable extremum seeking system with unknown control gain［J］.Conrot Theory&Applications，2013，30（4）：405-416.（in Chinese）

［18］MARTIN GUAYA，DENIS DOCHAIN.A time-varying extremum-seekingcontrolapproach［J］.Automatica，2015，51：356-363.

Sliding Mode Switching Extremum Seeking Control for MIMO Affine Nonlinear Systems

ZHANG Leia，HU Yunana，LI Jingb
（Naval Aeronautical and Astronautical University a.Department of Control Engineering；b.No.7 Department，Yantai Shandong 264001，China）

A sliding mode switching extremum seeking control method based on fractional-order integral was proposed for multi-input multi-output（MIMO）affine nonlinear systems.The original nonlinear system was decomposed into several subsystems and switching function was constructed by the output tracking error and the integral of the tracking error.Sliding mode switching extremum seeking control law was designed and method stability was proved strictly.Simulation results were presented to illustrate the advantages of this method by comparing with the existing method.

affine nonlinear system；extremum seeking；switching function；fractional-order

TP273.23

A

1673-1522（2016）03-0341-07DOI:10.7682/j.issn.1673-1522.2016.03.008

2016-03-14；

2016-04-20

國家自然科學基金資助項目（60674090）

張雷（1988-），男，博士生；胡云安（1966-），男，教授，博士，博導。