巧用三角形的外角

□安義人

巧用三角形的外角

□安義人

三角形的一邊與另一邊的延長線組成的角叫做三角形的外角.解答一些與三角形的角有關的問題時，別忘了靈活運用三角形的外角.

一、與角有關的求值問題

例1如圖1，CE平分∠ACD，F為CA延長線上一點，FG∥CE交AB于G，∠ACD=110°，∠AGF=20°，試求∠B的度數.

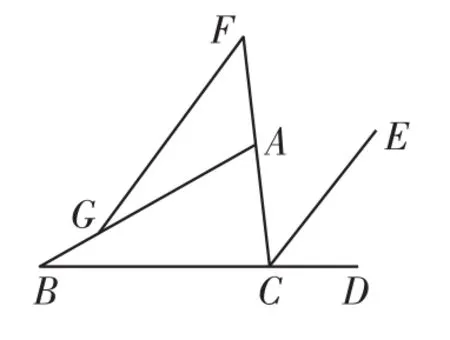
圖1

分析：顯見∠ACD=∠B+∠BAC.又∠ACD=110°，那么要求∠B的度數，關鍵在于確定∠BAC的度數.

解：因為CE平分∠ACD，

∠ACD=110°，

因為FG∥CE，

所以∠F=∠ACE=55°.

又∠AGF=20°，

所以∠BAC=∠F+∠AGF=75°.

因為∠ACD=∠B+∠BAC，

所以∠B=∠ACD-∠BAC=35°.

二、與角有關的證明問題

例2如圖2，點P是∠ABC和外角∠ACE的角平分線的交點.求

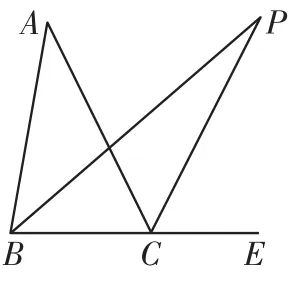
圖2

分析：顯見∠A=∠ACE-∠ABC，∠P=∠PCE-∠PBC.要證明∠P=∠A，那么只要證明∠PCE-∠PBC=（∠ACE-∠ABC）就可以了.

證明：因為CP、BP分別平分∠ACE、∠ABC，

因為∠PCE=∠P+∠PBC，

所以∠P=∠PCE-∠PBC

因為∠ACE=∠A+∠ABC，

所以∠ACE-∠ABC=∠A.

三、與角有關的探索問題

例3如圖3，△ABC中，AE平分∠BAC，∠C＞∠B，F為AE上的一點，且FD⊥BC于點D.

（1）請探索∠EFD與∠B、∠C的數量關系；

（2）如圖4，當點F在AE的延長線上時，其余條件都不變，判斷你在（1）中探索的結論是否還成立？如果不成立，∠EFD與∠B、∠C又有怎樣的數量關系，請說明理由.

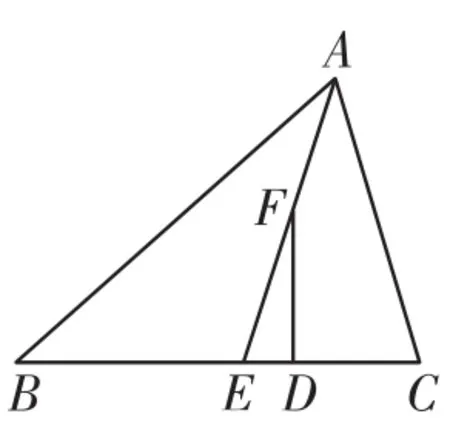
圖3

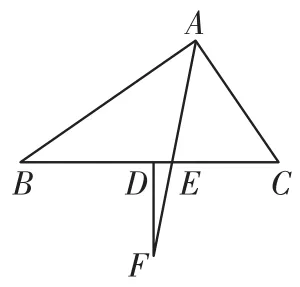
圖4

分析：無論是圖3，還是圖4，都有∠FDE=90°，那么∠EFD=90°-∠DEF.要探索∠EFD與∠B、∠C的數量關系，應考慮將∠DEF轉化，看看能否用∠B、∠C的代數式表示.

因為FD⊥BC，

所以∠FDE=90°，

∠EFD=90°-∠DEF.

因為AE平分∠BAC，

∠BAC=180°-（∠B+∠C），

所以∠DEF=∠B+∠BAE

（2）成立.證明思路與（1）類似.