非線性試驗數據的擬合方法

?

非線性試驗數據的擬合方法

針對目前數據擬合在試驗記錄與分析中的應用較為廣泛，以最小二乘法為基礎，以MATLAB軟件為輔助工具，研究分段線性函數的方法在非線性分布數據進行擬合的應用。經過擬合得到的分段線性函數物理意義明確，而且利用分段線性函數可以簡化計算，使試驗數據分析更為簡便、快捷。該數據擬合方法與解決問題的思路可為非線性試驗數據的擬合提供參考。

非線性數據點；分段線性函數；擬合；MATLAB

許多科學與工程結果的產生都來自于對試驗的記錄與分析[1]。試驗記錄的數據，通常是指試驗中所得到的數據點，例如在速度與位移的試驗中，所測得的速度與位移的關系將被表示為一個個的數據點。目前，在大多數情況下，數據的測試與儲存都是通過計算機進行的，一旦數據已知，科學、工程從業者會將其以不同的方式運用。通常，數據點將會被通過數學運算變為有普遍性的方程，從而得到數據之間的相互關系。

在科學和工程試驗中，所得到的數據點如果大致呈直線分布，這種情況較好處理；但在大多數情況下，其是非線性分布的，如文獻[2]中懸置的靜剛度隨著載荷的變化而變化，測試到的力—位移數據點為非線性分布，則數據的處理量較大，計算較為復雜，且非線性曲線中各個點的物理意義不是很明確。

本文針對將非線性數據點進行分段線性處理的問題，研究采用分段線性函數，利用最小二乘法[3]，擬合非線性函數的基本思路。利用MATLAB軟件，研究用分段線性函數擬合非線性函數的方法。

1 線性數據擬合的2種方法

假設由試驗得到的數據點為(xi,yi)，i=1,2,…,n，其大致呈線性分布，但不全處于同一條直線上。設數據點大致滿足的線性方程(擬合模型)為y=kx+b。由于數據點不全處于同一條直線上，在x相同時，y所對應值與通過線性方程計算得到的值之間存在一定的殘差，該殘差可用下式表示：

(1)

為后續求導計算方便，筆者使用殘差的平方和來衡量該殘差，殘差的平方和定義為：

(2)

由極值關系[4]可知，當E取最小值時，E對k和b的導數應等于0。現分別對k與b進行求導，并令其值等于0。

(3)

(4)

由式3和式4得：

(5)

(6)

求解式5和式6，得到：

(7)

(8)

同樣，可通過矩陣形式來解決該問題。假設擬合模型經過每個數據點，則有：

(9)

將上式寫成矩陣形式為：

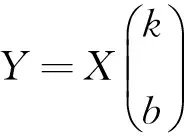
(10)

式10中，

由式10可知，只有k與b這2個未知數，卻有n個方程。根據矩陣與其轉置相乘的特點，筆者產生了減少方程數量的想法。由式10兩邊同乘X的轉置矩陣，得：

(11)

則：

(12)

假設有8個數據點(見表1)，應用MATLAB軟件求解式12，得到k=2.96，b=1.12；求解式7和式8，同樣得到k=2.96，b=1.12。線性擬合線段和數據點的關系如圖1所示。

表1 數據點

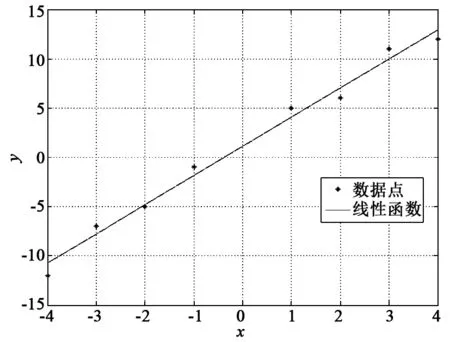
圖1 擬合方程與數據點(殘差平方和為6.811 2)

2 利用分段線性函數擬合非線性數據的方法

對于呈非線性分布的數據來說，用線性方程來

擬合非線性數據，得出的結果，其偏差大。對于非線性數據，可視為一段段的線性函數組合而成，因此，筆者在此研究了利用分段函數來擬合非線性數據。

設試驗得到的數據點如圖2所示，圖中的x與y表示為(xi,yi)，i=1,2,…，n。

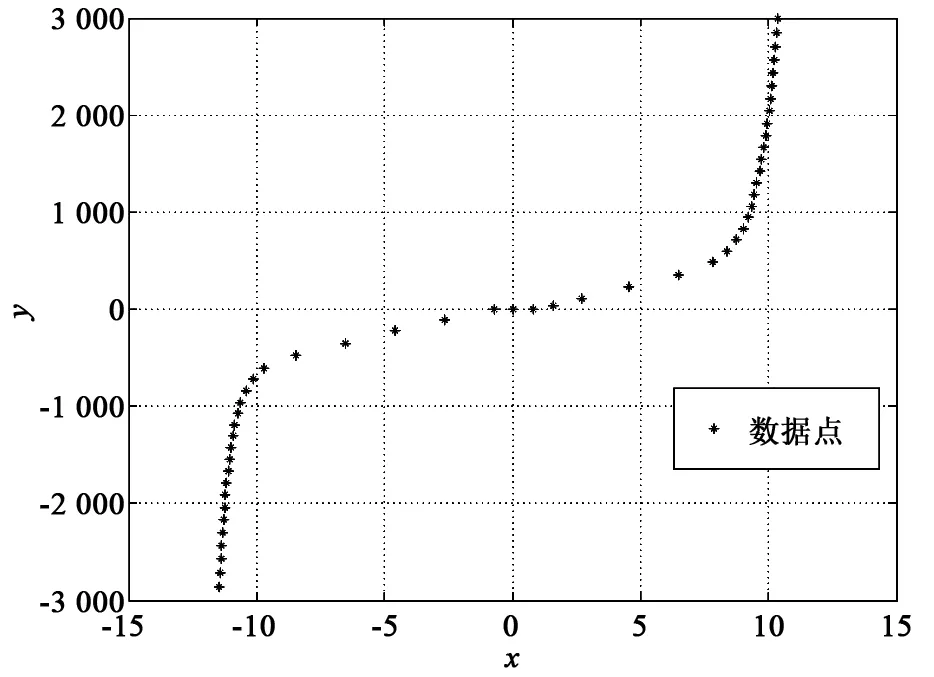
圖2 非線性數據點

已知數據點經過原點，現用5段分段線性函數(見圖3)來擬合圖2中的數據點，圖3中的分段函數為：

(13)

利用求極值的方法來解決該問題為常規思路，但計算過程復雜。筆者在此應用MATLAB軟件中的fmincon函數，來求解式13中的變量ki(i=1,2,3,4,5)與a、b、c、d的值。

圖3 5段分段線性函數

MATLAB工具箱中的fmincon函數[5]，是一種求解有約束的優化問題函數。現設目標函數為各個數據點的殘差平方和，由式2和式14，可得到：

(14)

將式14變成MATLAB軟件中的目標函數，該函數具有ki(i=1,2,3,4,5)與a、b、c、d等9個變量，根據fmincon函數的使用要求，還需獲得函數約束條件，由式14與圖2、圖3，可得到其約束條件為：

(15)

式中，xmax為數據點中x的最大值；xmin為數據點中x的最小值。

對圖2中的數據，根據MATLAB軟件中的fmincon函數的語法編寫程序，計算得到的參數為：k1=2 937,k2=474,k3=54,k4=59,k5=2 213,a=-10.9,b=-9.6,c=8.3,d=9.6。

5段分段線性函數與數據點的關系如圖4所示。通過同樣方法，可用3段分段線性函數對曲線進行擬合，也可以用7段乃至更多段進行曲線擬合，若用3段分段線性函數來擬合圖2中的數據點，可得到k1=2 746,k2=76.8,k3=1 861,a=-10.7,b=9.2。3段分段線性函數與數據點的關系如圖5所示。

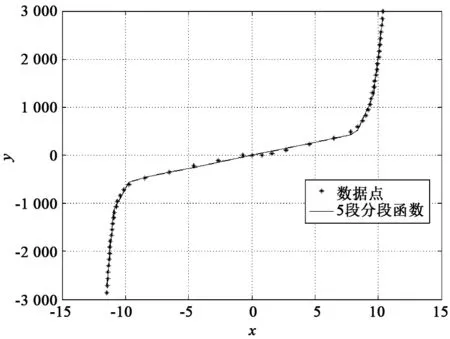
圖4 5段分段線性函數與數據點的關系 (殘差平方和為229 330)

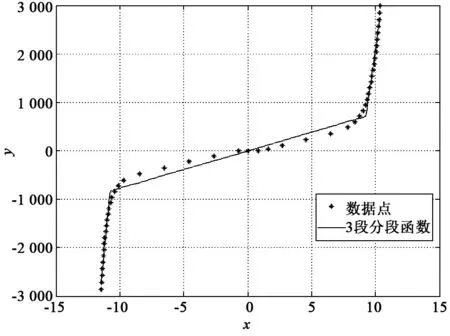
圖5 3段分段線性函數與數據點的關系 (殘差平方和為697 788)

對比圖4和圖5可知，5段分段線性函數所得的殘差平方和遠小于3段分段線性函數所得的殘差平方和，故運用5段分段線性函數的擬合效果較好。一般來說，在工程應用上，5段擬合足夠滿足基本需求。

3 結語

本文研究了通過線性函數或分段線性函數擬合數據的方法，推導了用線性函數擬合線性數據點、用分段函數擬合非線性數據點的計算方法。本文的數據擬合方法與解決問題的思路，為非線性試驗數據的擬合提供了參考。

[1] Amos G, Vish S. Numerical methods for engineers and scientists[M]. America: Wiley, 2011.

[2] 劉祖斌，劉英杰. 發動機懸置設計中的動、靜剛度參數研究[J].汽車技術，2008(6)：21-23.

[3] 田垅，劉宗田. 最小二乘法分段直線擬合[J].計算機科學，2012(S1)：482-484.

[4] 同濟大學數學系. 高等數學[M].6版. 北京：高等教育出版社，2010.

[5] 周智峰，張明. 基于MATLAB的最優化問題求解通用程序的實現[J].計算機科學，2004(6)：29-32.

責任編輯 鄭練

李廣龍，魏政君，上官文斌

(華南理工大學 機械與汽車工程學院，廣東 廣州 510641)

A Method for Fitting Nonlinear Experimental Data

LI Guanglong, WEI Zhengjun, SHANGGUAN Wenbin

(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510641, China)

In the analysis of experiment data, the data fitting is widely applied, but sometimes the fitting process is very complicated. In order to simplify the analysis process, introduce a fitting method for nonlinear data. The method is based on the least squares method to fit the nonlinear dada with piecewise linear functions, and using the MATLAB software as toolbox. The constant in the piecewise linear functions has clear meanings. Use the fitted piecewise linear functions as substitute for nonlinear data, the analysis for the experiment data is more simple and efficient. The data fitting method and the idea of solving the problem are provided， and the results provide a reference for the fitting of nonlinear experimental data.

nonlinear data, piecewise linear functions, fitting, MATLAB

yi=kxi+b i=1,2,…,n

Ei=

李廣龍(1982-)，男，實驗師，主要從事汽車性能測試、汽車實驗臺架設計等方面的研究。

2016-03-29

TB

A