應用直線回歸和時間序列建立診療人次預測模型
●孫希蓉
應用直線回歸和時間序列建立診療人次預測模型
●孫希蓉
目的:運用統計學方法對醫院診療人次進行預測,為醫院的現代化管理提供依據。方法:應用直線回歸和時間序列建立預測模型。結果:通過時間序列算出各季度的季節比率,剔除季節比率,通過對相關系數r的檢驗,證明線性關系顯著,建立預測模型YC=143929.8+5515.05t,在此基礎上預測2017年和2018年診療人次的點估計值以及95%置信區間下的區間估計值。結論:該預測方法比較合理,接近實際,為醫院領導各項計劃的制定,各項政策的正確實施,正確的決策提供可靠的數據保證和理論支持。
診療人次;預測;直線回歸;時間序列
現代醫院管理中,統計預測已經逐漸成為一種不可或缺的工具。醫院診療人次是反映醫院工作效率的一項重要指標,診療人次的多少在很大程度上可以反映醫院的規模、醫療質量和技術水平。對醫院診療人次進行分析和預測,可以為制度醫院工作計劃和決策管理提供依據,進而最大限度的滿足病人需求,以提高醫院的社會效益和經濟效益。[1]大家都知道診療人次與多種因素相互關聯,既有長期趨勢、季節干擾,又有隨機因素,給我們的預測帶來了很大難度,因此本文運用了直線回歸和時間序列,考慮長期和季節兩個主要因素,增加對該指標的預測精度。
1 資料來源
本文資料來源為我院2006年—2016年醫院工作報表,資料可靠、準確(見表1、圖1)。從圖表中可以看到我院診療人次從2006-2016年有比較明顯的季節波動和長期持續增長趨勢。
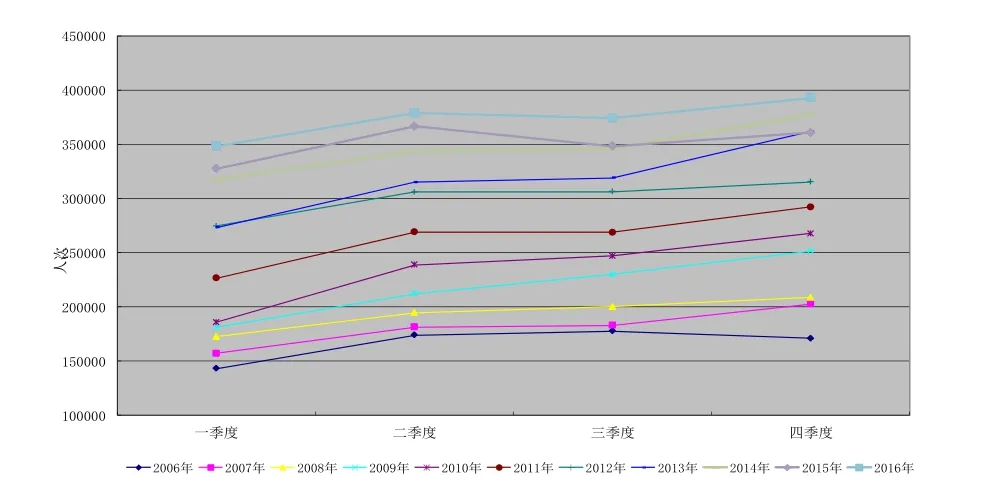
圖1 2006年-2016年各季度診療人次折線圖
2 方法與結果
(1)運用時間序列算出各季度的季節比率,反映診療人次的季節變化規律。公式如下:季節比率=同一季度平均值/各年份總平均數。(計算結果詳見表1)
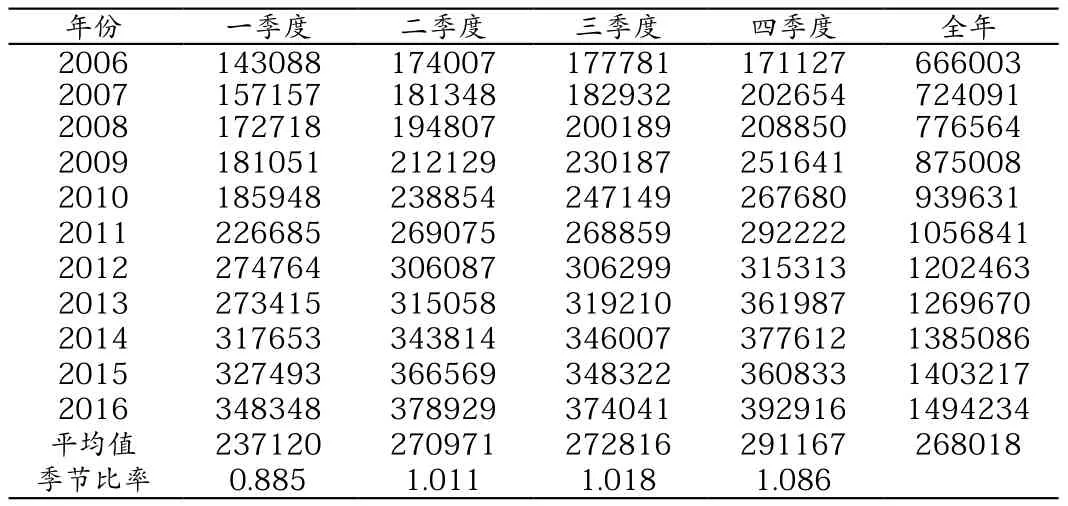
表1 診療人次與季節比率
(2)用實際診療人次除以季節比率算出剔除季節因素的診療人次(Y)
(3)以時間序號t為自變量,剔除季節因素的診療人次Y為因變量,繪制散點圖(見圖2),我們從圖中可以明顯地看到各個點分布在一條直線的附近,即自變量t和因變量Y有較強的線性相關關系。在此基礎上計算二者的相關系數得到r=0.981,進而對相關系數進行t檢驗得到P<0.01,說明這兩項指標具有高度的直線相關關系。
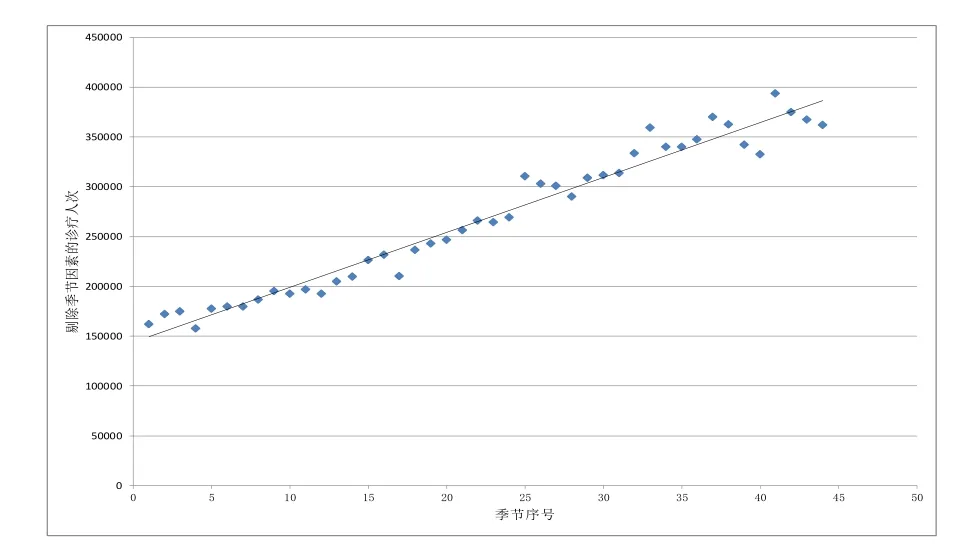
圖2 兩變量散點圖
(4)根據圖形以及數據資料建立剔除季節因素的診療人次和時間序號的直線回歸方程,以此來推測診療人次的長期趨勢。該方程為:
YC=143929.8+5515.05t
(5)對于同一資料,如果回歸系數有統計學意義,那么相關系數也一定有統計學意義,反之亦然。[2]由上已知相關系數r有統計學意義,所以該直線方程有統計學意義。
3 預測
(1)從圖表和直線回歸方程中我們不難看出在剔除了季節波動的因素后,我院診療人次在這11年的時間中始終呈現比較穩定的發展態勢,診療人次逐年呈直線上升。綜上,我們可以根據直線回歸方程計算出長期趨勢影響下的診療人次,再用該診療人次乘以各季度的季節比率預測2017年和2018年診療人次的點估計值以及95%置信區間下的區間估計值(見表2)。
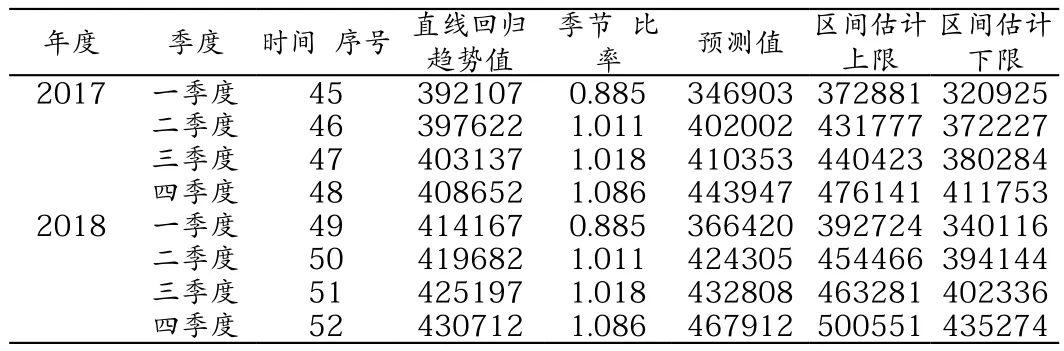
表2 各季診療人次預測值
(2)驗證:我院2016年第四季度實際診療人次為392916人次,四季度實際診療人次與預測點估計值僅相差27065人次,相差6.9個百分點,而且實際診療人次在我們預測的區間估計范圍中,由此可見,該預測方法比較合理,接近實際。
4 分析討論
每個醫院的診療人次都受到多種因素的影響,在此我們主要考慮了長期趨勢和季節變動這兩個因素,通過預測診療人次,不但看到了該指標的長期變動趨勢,還明確地反映了季節波動情況,能更加合理地利用衛生資源及配套設施,用最少的勞動消耗,創造出更多的勞動成果,為醫院領導各項計劃的制定,各項政策的正確實施,正確的決策提供可靠的數據保證和理論支持。
利用本研究建立的模型,是在假設除長期趨勢和季節波動以外的其他影響診療人次的因素呈相對穩定的基礎上進行的,因此,一旦影響因素發生重大變化,需要重新分析數據,選擇新的預測模型。無論完美的模型都會與實際情況有一些偏差,參考置信區間的預測結果會使具體管理、決策工作有一定的彈性空間,更符合實際工作需要。
(作者單位:天津市第五中心醫院)
[1]張璟.醫院門診量的長期趨勢及季節變動分析[J].中國醫院統計,2011,18(3):274-276.
[2]陳峰.醫用統計方法[M].上海:復旦大學出版社,2009.113.
[3]姜玉蓮,胡鵬.應用馬爾可夫預測模型對門診就診人次的預測[J].當代醫學,2009,15(30):28-29.
[4]黃小瓊.最小二乘法預測門診人數[J].中國病案,2012,13(4):62-63.
[5]沈寧,段司鳳,阮文寧.“十二五”期間門診人次和住院人數的預測[J].中國病案,2011,12(10):48-50.
[6]方紅.某院門診人數與住院人數的預測與相關分析[J].中國醫院統計,2011,18(4):336-338.

