基于儲能調度模式的分布式光伏兩階段多目標就地消納模型

李　鵬，華浩瑞

(新能源電力系統國家重點實驗室(華北電力大學)，河北保定071003)

?

基于儲能調度模式的分布式光伏兩階段多目標就地消納模型

李鵬，華浩瑞

(新能源電力系統國家重點實驗室(華北電力大學)，河北保定071003)

隨著分布式光伏接入配電網容量的提高，分布式光伏就地消納模型成為日益重要的課題。提出了一種基于儲能調度模式的分布式光伏兩階段多目標消納模型。該模型以儲能調度策略為主要控制變量并配合機組出力，以分布式光伏消納率最大為優先目標，以系統運行成本最小為次要目標，計及儲能運行約束等必要約束條件。針對建立的模型采用JAS算法配合分段線性化的混合整數規劃，并結合智能單粒子算法構成的混合算法進行求解。通過一個算例驗證了該模型能在不同滲透率情況下最大化光伏消納率的同時最小化運行成本，使得模型更加符合實際和具有應用價值。

儲能調度模式； 兩階段優化；多目標；光伏消納；JAS算法；智能單粒子算法

0　引言

2015年3月，《國家能源局關于下達2015年光伏發電建設實施方案的通知》出臺，要求全年新增光伏電站建設規模達17.8 GW，并優先建設35 kV以下、20 MW 以下的接入配電網的分布式光伏電站項目[1]。根據中國光伏資源分布特點，未來中國光伏發電發展將呈現大規模、高集中的開發趨勢[2]。而隨著分布式光伏發電接入容量的提高，研究配電網光伏消納能力及提高光伏消納能力的措施具有重要的現實意義[3-5]。

從系統的角度看，不同的電力系統對分布式光伏出力的接納能力并不相同。面對這樣的情況，如果系統有充足的儲能設備，則光伏的輸出相對容易充分消納，可更容易實現對光伏輸出的平穩消納而且能夠滿足系統的安全穩定需求，從而提高光伏的消納能力。文獻[6]基于某一實際系統饋線，結合當地實際負荷及光伏規劃容量，利用隨機場景方法，分析了系統饋線的最大光伏消納能力；文獻[7]針對大規模并網光電消納容量計算問題，構建了一種考慮網絡傳輸約束的消納分析模型；文獻[8]制定了以分布式光伏消納最大化為目標的主動負荷需求響應方案。此外，還有文獻[9-10]針對地區特點建立模型計算了其光伏消納容量。然而，當分布式光伏滲透率較低的情況下，傳統的僅以光伏消納率最高為目標的消納模型得出的最優解通常不是唯一的，這是因為此時消納率容易達到100%，而且無法計及含分布式光伏配電網的運行效益。因此需要重新建立模型并在模型中計及其他目標，使得模型更加合理和符合實際。

分布式光伏的滲透率定義為光伏1 d出力總容量與本區域1 d負荷容量的比例。分布式光伏集群相對于電力系統的不同滲透率為就地消納帶來了不同的挑戰，本文討論了光伏滲透率低與滲透率高這兩種情況。

本文主要考慮采用儲能調度模式提高分布式光伏消納率并提高含分布式光伏配電網的運行效益，提出一種分布式光伏集群兩階段多目標優化消納模型。該模型包含優先目標(光伏消納率最大)和次要目標(系統運行成本最小)。事實上，該模型存在一個分布式光伏邊界滲透率，當光伏滲透率較小于該邊界滲透率的情況下，優先目標容易達到上限，因此需要模型以運行成本最小為目標，系統的安全較易保證，備用需求相對較小，因此儲能單元的作用主要還是提供合理的熱備用與調峰能力，并在一定程度上實現削峰填谷；當光伏滲透率大于該邊界滲透率的情況下，儲能是備用的重要組成部分，優化的重點是保證安全，通過合理的儲能調度實現光伏盡可能多的安全消納，此時希望模型主要考慮優先目標。

然而，在實際運行中，難以判定邊界滲透率，而傳統優化模型無法自動地針對任意情況對該兩階段消納模型進行求解。因此本文提出了基于JAS算法的兩階段多目標優化消納模型求解方法。通過算例表明，本文模型可以自動地在優先實現最大化光伏消納率的同時，盡量滿足系統運行成本最小。

1　儲能調度模型

本文根據分布式光伏滲透率針對2種情況進行分析：

第1種情況，分布式光伏滲透率較低。此時光伏功率輸出的隨機性與不確定性相對較小，系統有足夠的能力對這些不確定性因素加以消納，因此帶來的負面影響較易消除。此時可以將整體經濟性作為優化目標，在保證網絡安全的情況下做到光伏輸出的幾乎100%就地消納，同時實現經濟性的最優化。之所以不能完全做到100%是因為在分鐘甚至秒級的時間尺度上可控機組的爬坡率限制以及儲能出力變化速率限制。主要思路是首先令光伏集群以最大功率點跟蹤(Maximum Power Point Tracking, MPPT)模式全額輸出，其余發電單元配合儲能，在光伏達到最大消納的基礎上，通過合理的調度計算，以綜合經濟性的最優為目標實現包括經濟性等多目標的整體的優化。

第2種情況，分布式光伏滲透率較高。此時的特點是需要一定的優化才能做到光伏充分消納，同時也可能有余力對經濟性進行一定的優化。光伏較大程度的不確定性成為了消納率提升的最大障礙，因為這樣的問題很可能導致安全約束、系統調峰、備用等約束無法滿足等問題的出現。因此，在第1種情況下需要以安全可靠為第一要素，此時將根據需要限制部分光伏出力(亦即“棄光”)，迫使光伏按給定的要求減少出力以維持安全性和系統穩定，但是這樣做會導致能量的損失。考慮到儲能相比于火力發電等傳統電源來說擁有更高的靈活性，在合理的儲能調度優化基礎上，可通過對儲能運行時間與容量的合理調度，實現減少棄光的目標，從而提高光伏發電的就地消納能力。

分布式光伏的功率輸出曲線和負荷曲線通過日前預測獲得。在所研究的電力系統中，除了分布式光伏集群、負荷與儲能設備以外還裝配有火力發電機組作為可控電源。

系統的目標函數以光伏集群的功率消納率最高為優先目標，在保證消納的情況下，兼顧其他目標。首要目標為光伏消納率F1如式(1)所示。對于所給定的光伏出力預測曲線PPV，0(t)，實際消納為PPV(t)，那么在日前計劃中的光伏消納率F1可以通過消納的光伏功率總和與光伏實際出力總和之比來表示。

(1)

式中：T為總時段數。

兩階段優化模型的次要目標采用多目標模型。次要目標的第1個子目標為經濟成本，主要考慮了發電成本如式(2)所示，此外為了計及含分布式光伏接入配電網的節能減排效益，目標函數中還應計及網損成本如式(3)所示，任意時段的網損成本按該時段的外網分時電價水平計算價值，從而與發電成本相整合。

(2)

式中：C1為經濟成本；G為總機組數；fg() 為機組g所對應的成本曲線，已經包含了燃料成本、運行維護成本、設備折舊成本等必要成本；Pg(t)為機組g在t時段的出力；ΔT為每個時段對應的時長，本文中取為1 h。

(3)

式中：C2為網損成本；Ploss,l(t)為t時段線路l的網損，總線路數量為L；p(t)為t時段外網分時電價水平。

因此，所構成的第一個子目標經濟成本為f1如式(4)所示：

(4)

第2個子目標為儲能電量越限懲罰項。一般文獻通常直接采用儲能電量上下限約束來對儲能中電量進行約束從而避免其越限[11]。然而在實際中，在某些情況下允許儲能電量越限是有利的，只需要對儲能電量越限加入一定的懲罰項計入目標函數即可，但是仍然希望儲能電量越限程度越小越好。而這樣的模型更加符合實際也具有更好的效益。儲能電量越限的目標函數懲罰項，即次要目標的第2個子目標f2如式(5)所示，其中儲能電量越限百分比ΔSSB(t)如式(6)所示。

(5)

(6)

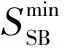
因此，兩階段模型的次要目標如式(7)所示：

(7)

式中： γ1與γ2為權系數。

整體優化模型為，首先滿足消納率最大化目標maxF1，如果在達到100%消納的情況下，考慮次要目標minF2的優化。當優化模型的優先目標達到最優且最優解不唯一的時候，則最優解在滿足優先目標最優的前提下由次要目標對應的優化模型來決定。

所要滿足的儲能相關的約束條件包括儲能充放電功率上下限約束，儲能電量與儲能充放電功率關系的約束，以及儲能首末電量約束。

針對本文項目基于的分布式光伏示范工程所在地區的特點，本文研究中采用的儲能單元形式為集中式蓄電池組。所用蓄電池的數學模型為：

儲能充電時和放電時的電能模型如式(8)和式(9)所示：

(8)

(9)

式中：PSB(t)為t時段蓄電池功率，以放電為正方向；ηin為充電效率；ηout為放電效率。

此外，蓄電池儲能還需要滿足充、放電功率上下限約束：

(10)

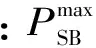
此外，由于本文考慮的是1 d內的消納模型，為了維持電能穩定以及保證次日的運行調度，需要引入調度周期首末電能約束如式(11)所示；在實際運行中，儲能1 d首末電量一般可取為儲能容量的一半。

(11)

式中：SSB(0)表示第一時段前的儲能電量；SSB(T)表示1 d最后1個時段末的儲能電量。本文中儲能電量只考察每個時段始末，即1 d 25個時刻的儲能電量情況。

在日級時間尺度上的儲能運行方式研究中，假定儲能的折舊相對較小，因此忽略儲能容量的變化對模型的影響。

此外，所需要滿足的約束包括機組出力上下限約束如式(12)所示、節點電壓約束如式(13)所示、以及聯絡線傳輸功率約束如式(14)所示。

(12)

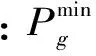
(13)

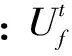
(14)

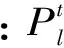
此外，假定該含分布式光伏接入的配電網系統已經向外網購買了必要的旋轉備用以應對光伏出力較小時間尺度上的波動性，該購買容量的確定可以通過優化配置模型確定，不是本文研究重點，因此假定該購買的旋轉備用是充足的。

2　模型求解算法

上述光伏集群就地消納問題構成了多個目標的優先級與目標函數值相關聯而形成了分階段的非線性多目標優化問題，該問題不適合用常規的混合整數線性規劃方法(常規MILP)加以求解，對此可采用Jump and shift method[12]迭代算法(簡稱JAS)配合分段線性化的混合整數規劃算法，并結合智能單粒子算法(Intelligent Single Partical Optimization，ISP)[13]構成的混合算法求解。

混合算法的主體迭代算法JAS，是一種提高復合型優化問題求解效率的有效方法。設有兩個優化問題，分別記為優化問題A：

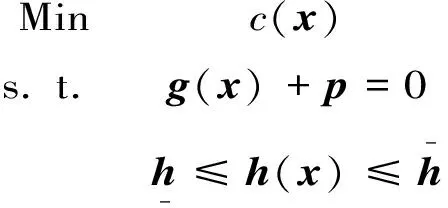
(15)

以及優化問題B：

(16)

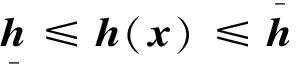
不同于傳統的代入求解，JAS算法采用分開計算、循環整合的方式對這兩個相互耦合的問題進行整體優化，并且避免了計算量的明顯增加；此外，其內部的小范圍松弛也為過程中的尋優提供了更多的機會。在JAS方法中定義3組優化變量形成的向量如下：

(17)

式中：F-1(A)|p為在給定的p值下優化所得解x；G-1(B)|x為在給定x的基礎上優化所得解y；K-1(B)|x為給定x的基礎上優化所得解p。這一通過求解優化子問題而獲得適用于另一問題的優化變量值的過程被稱為Jump過程。

同時，定義如下的Shift因子χ用于調節算法的收斂速度：

(18)

式中：x(i)為第i個變量；x(i)new為在χ的限制下所得的新x(i)值。

基于JAS可實現分階段多目標的優化計算。整體方法為建立計及光伏消納率最大化與綜合經濟性最優的分階段目標，構建多目標優化運行復合問題，其中優先考慮光伏消納率最大化；在首要目標得到滿足的情況下，以其保持最大為約束條件、以次要目標為優化目標進行第二階段的優化計算。

混合整數規劃MILP可以解決的機組組合問題構建為問題A，潮流與損耗優化的部分構建為問題B。其連接關系為：

(19)

式中：G為系統中機組數量；PLD(t)為t時段系統總的凈負荷功率，即系統總負荷功率減去光伏發電功率；PLOSS(t)為t時段全系統的損耗。通過潮流計算即可獲得網絡中包括潮流與節點電壓等各項參數，由Shift因子χ松弛后的機組輸出功率可在松弛范圍內以光伏消納率進一步提高或損耗最低為目標進行尋優求解工作。

問題B構建為變量搜索范圍有限的優化問題，采用智能單粒子算法ISPO實現快速求解。ISPO只需要在一個粒子的基礎上通過特殊的迭代循環實現優化求解，尋優準確，計算快速。

將ISPO算法用于求解問題B，則優化變量為某個靜態時間斷面下各單元的出力情況，其變量約束除設備本身以外，還受到Shift因子χ的限制。

看到盧一平語噎,郝桂芹轉身走了。走幾步,回頭又說。你再想想,將來你兒子去城市買房,開發商用雜志和你結算嗎？

在ISPO中定義了“子矢量”的概念。稱用矢量表示的解為“解矢量”，即靜態時間斷面下的矢量p，則子矢量為這個解矢量的片段，具體含義為若干機組的出力組合。ISPO算法的唯一粒子是整個解矢量，維數為D，可劃分為m個互不重疊的片段，則稱將解矢量分解為m個子矢量。每一個子矢量都擁有自己的位置zj與速度vj，j=1,…,m。子矢量的劃分取決于按照變量之間的關聯，關聯緊密的變量在劃分到同一子矢量后，尋優能力通常會更強。每一片段允許不連續，但這實際上等價于對變量進行某種重新排列，因此為了敘述簡單起見，這里依然用子矢量連續的形式表示。

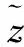
(20)

(21)

(22)

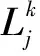
3　求解方法流程

算法的流程為：

(1)以光伏就地消納率最大為目標，以系統和設備限制為約束，對問題A進行MILP機組組合計算，并將出力計劃送入問題B。

(2)問題B中在Shift因子χ范圍內，通過ISPO計算損耗并修正平衡等式，在變量優化范圍內以光伏就地消納率最大為目標進行尋優。

(3)如果光伏消納率已經達到最大，則修改模型，加入保持光伏消納率最大的約束和綜合經濟性最優的目標，進入步驟4；否則如果不滿足收斂條件，就重復步驟1；若光伏消納率還沒有達到100%但已經達到收斂條件，則轉步驟7。

(4)以綜合經濟性最優為目標，在保持光伏消納率最大的基礎上對問題A進行MILP機組組合計算，并將出力計劃送入問題B。

(5)問題B中在Shift因子χ范圍內，通過ISPO計算損耗并修正平衡等式，在變量優化范圍內以綜合經濟性最優為目標進行尋優。

(6)如果綜合經濟性最優的計算已經收斂，則轉步驟(7)；否則轉步驟(4)。

(7)停止計算，輸出結果。

4　算例

本文基于IEEE九節點系統構建了改進的含分布式光伏接入的系統。在算例中有3臺發電機組分別為Gen1、Gen2、Gen3分別接入節點1、2、3，容量依次為400 MW，400 MW，200 MW，其中節點1通過PCC與外網連接，可以由外網向該含分布式光伏的配電網傳輸功率，為了保證外網的安全可靠性，因此不考慮節點1通過PCC向外網售電的情況。在負荷節點5、6、8分別接入分布式光伏，接入容量相等，接入總容量在具體算例中根據要考察的滲透率而定；在節點9接入集中式儲能系統蓄電池組，其配置容量為250 MW·h，充放電功率上限50 MW。本文主要研究分布式光伏有功功率的消納模型，因此假定系統中無功功率充足而不考慮無功運行特性。

算例1：光伏滲透率較低的情況。分布式光伏集群的總容量為250 MW，滲透率為20%。備用容量取負荷的10%及光伏計劃的20%，且不考慮機組檢修和突發性誤差等問題。系統中光伏預測曲線PV與負荷預測曲線PL如圖1所示。

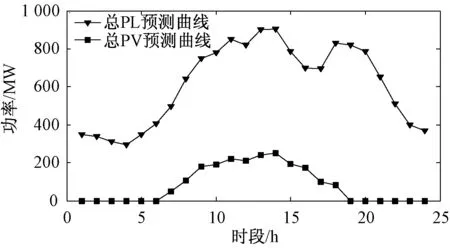
圖1　算例1低滲透率時負荷與光伏預測

采用本文的儲能調度模式進行求解，可以得到結果該算例中可以做到光伏100%消納，因此求解方法中的優化目標自動調整為綜合經濟性即次要目標。在不使用儲能的情況下，全調度周期的綜合成本為106 858.7元，光伏就地消納率100%；在加入儲能的情況下，全調度周期的綜合成本為103 357.7元，光伏就地消納率為100%。這種情況下，模型的優先目標消納率最高，容易得到滿足且滿足時的最優解不唯一，因此模型按照次要目標運行成本最小進行優化調度。

在算例1中，儲能主要作用是小額度的削峰填谷，由于火電機組的燃料成本曲線的斜率隨著其出力的增大而增大，因此通過儲能的削峰填谷作用可以讓機組盡量運行在效率較高的低斜率部分，從而降低運行成本。事實上，算例1中綜合成本降低了3.3%，各機組以及儲能充放電狀況如圖2所示。

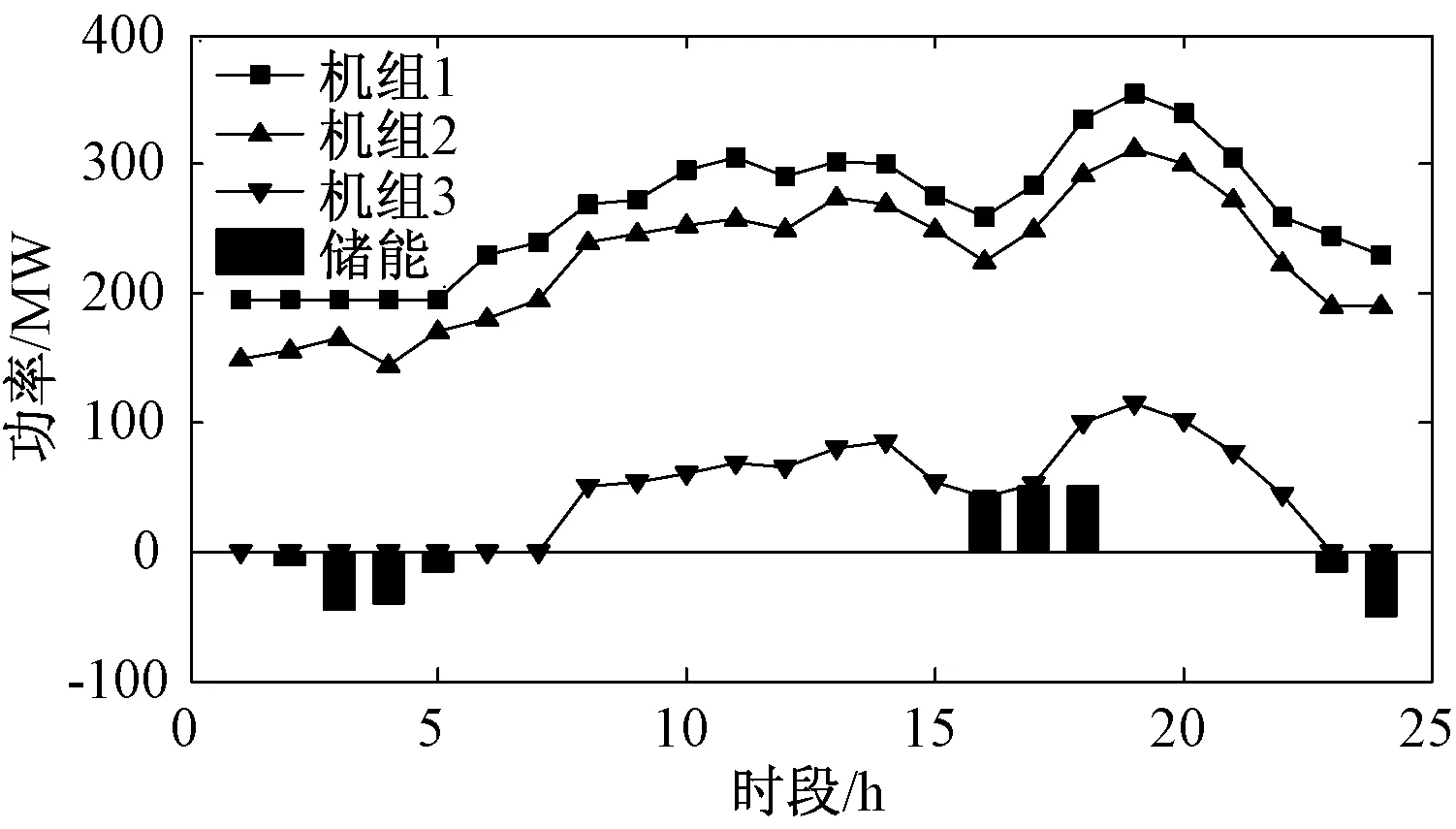
圖2　算例1消納光伏策略

算例2：同算例1，只按比例改變光伏的總裝機容量，將其提高到875 MW，此時滲透率為70%，這個數據意味著在光伏輸出高峰時對其他發電單元有明顯的替代效果。高滲透率下系統中光伏預測曲線PV與負荷預測曲線PL如圖3所示。

圖3　算例2低滲透率時負荷與光伏預測

在不使用儲能的情況下光伏消納率為98.17%，綜合成本為65 177.83元；使用儲能的情況下，光伏消納率提高到100%，綜合成本為63 831.52 元。可以看出，儲能的合理調度實現了光伏就地消納率的提升，將本來難以消納的部分也得以充分利用，光伏消納率提高了1.83%，實現了就地充分消納；綜合成本降低了2.06%，相比之下效果沒有光伏滲透率較低的情況更顯著，這是因為當分布式光伏滲透率較高時，可以大大降低機組出力，使得機組更傾向于運行中燃料成本曲線的高效率部分，而使得通過儲能進一步提高效率的空間相對有限，所以通過儲能削峰填谷的成本下降效益沒有算例1顯著。

在這種情況下，模型按照優先目標進行優化調度，當優先目標既光伏消納率達到最大時，此時優化運行結果唯一；事實上，算例2中的各機組出力曲線以及儲能充放電狀況如圖4所示。

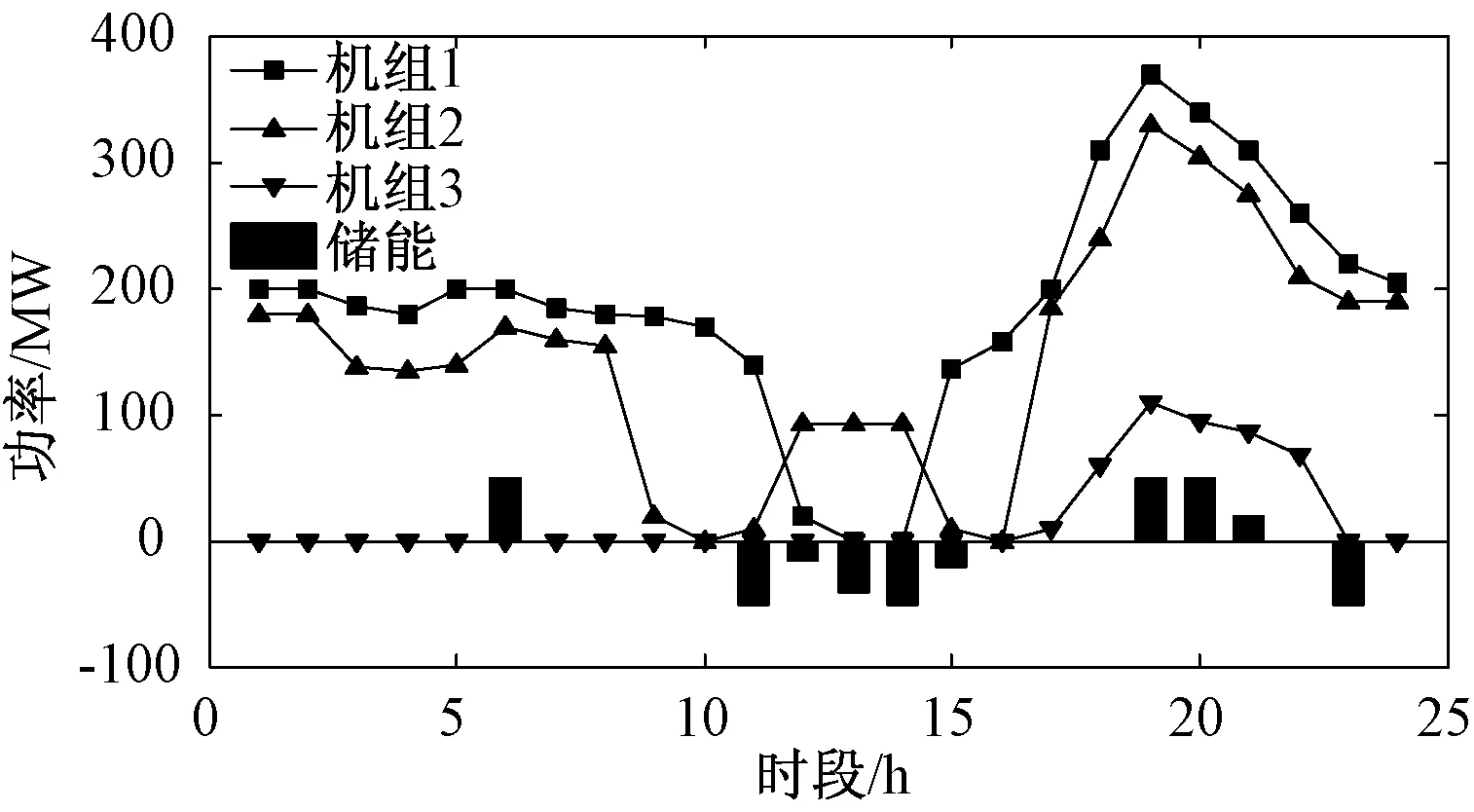
圖4　算例2消納光伏策略

具體分析儲能的作用可以看出，在光伏高峰階段儲能主要是吸收能量，而在晚上負荷小高峰但光伏無輸出的情況下，儲能放電，實現了光伏功率的更充分利用，整體滿足合理利用的要求。在本文2個算例中，儲能的1 d各時段電量情況如圖5所示。在算例1中，儲能的作用主要是削峰填谷，因此其電量在負荷高峰時期較低；而在算例2中，儲能調度的主要目的是提高光伏消納率，因此在光伏大量并網時充分充電，其電量在光伏出力大時較高。

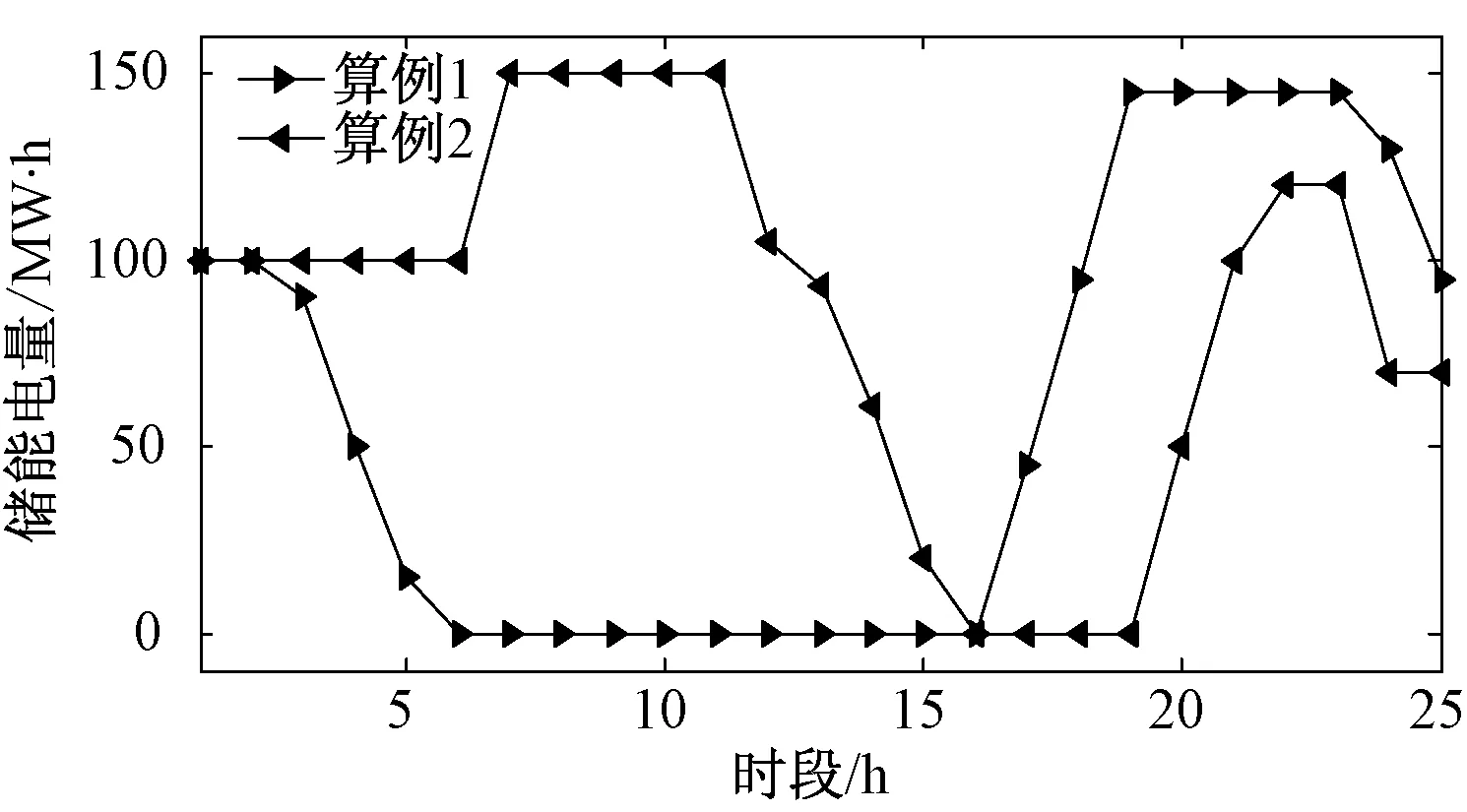
圖5　算例1和算例2的1 d各時段儲能電量情況

5　結論

本文提出了一種基于儲能調度模式的分布式光伏集群兩階段多目標優化消納模型。本文模型可以在優化光伏消納率的同時，更好地兼顧系統運行成本最小化的目標。通過算例說明：

(1)在分布式光伏滲透率較高時，采用本文儲能調度模式相比于不采用儲能調度模式時，可以較好地提高光伏消納率。

(2)當分布式光伏滲透率較低的情況下，采用儲能調度模式對分布式光伏消納率的提升沒有顯著作用，當滿足優先目標最優時的最優解不唯一，此時模型可以自主地計及次要目標即系統運行成本最低，制定經濟的調度策略。

(3)當分布式光伏滲透率較高的情況下，模型自主地以優先目標即消納率最大為目標，采用儲能調度模式對分布式光伏消納率的提升有顯著作用。

(4)提出的混合智能算法使用于求解類似本文的兩階段多目標優化模型，具備較好求解效果。

[1]劉皓明，陸丹，楊波，等. 可平抑高滲透分布式光伏發電功率波動的儲能電站調度策略[J]. 高電壓技術，2015,41(10): 3213-3223.

[2]白建華，辛頌旭，賈德香，等. 中國風電開發消納及輸送相關重大問題研究[J]. 電網與清潔能源，2010，26(1)：14-17.

[3]孫卓新，朱永強，倪一峰，等. 基于粒子群算法的含光伏電站的配電網無功優化[J]. 電力建設， 2014， 35(4) : 25-30.

[4]陳煒, 艾欣, 吳濤, 等. 光伏并網發電系統對電網的影響研究綜述[J]. 電力自動化設備, 2013, 33(2): 26-32.

[5]魏磊, 姜寧, 于廣亮, 等. 寧夏電力系統接納新能源能力研究[J]. 電網技術, 2010, 34(11): 176-181.

[6]趙波，韋立坤，徐志成, 等. 計及儲能系統的饋線光伏消納能力隨機場景分析[J]. 電力系統自動化, 2015，39(9)：34-40.

[7]歐陽聰，劉明波. 考慮網絡傳輸約束的并網光伏發電消納容量計算[J]. 電力系統保護與控制，2016，44(5):17-23.

[8]湯奕，魯針針，伏祥運. 居民主動負荷促進分布式電源消納的需求響應策略[J]. 電力系統自動化，2015，39(24):49-55.

[9]姚天亮，鄭海濤，楊德洲，等. 甘肅河西500萬kW光伏就地消納及調峰分析[J]. 中國電力,2014，47(3)：14-18.

[10]寧光濤，謝海鵬，別朝紅，等. 海南電網分布式光伏消納能力評估[J]. 南方電網技術，2015，9(5)：59-65.

[11]桑丙玉，王德順，楊波，等. 平滑新能源輸出波動的儲能優化配置方法[J]. 中國電機工程學報，2014，34(22)：3700-3706.

[12]CHEN S X, GOOI I H B.Jump and shift method for multi-objective optimization[J]. IEEE Transaclions on Industrial Electronics, 2011, 58(10): 4538-4548.

[13]紀震，周家銳，廖惠連，等.智能單粒子優化算法[J].計算機學報，2010，33(3)：556-561.

Two-stage Multi Objective Consumption Model for Distributed Photovoltaic Based on Energy Storage Scheduling Mode

LI Peng, HUA Haorui

(State Key Laboratory of Alternate Electrical Power System With Renewable Energy Sources,North China Electric Power University, Baoding 071003, China)

With the increase of the distributed photovoltaic (PV) capacity connected to distribution network, distributed photovoltaic consumption model has become an increasingly attractive topic. This paper proposed a two-stage multi-objective consumption model for distributed PV based on energy storage scheduling mode. The proposed model uses energy storage scheduling strategy, combining with the unit output as the main controllable variables, while the maximizing consumptive rate of PV is considered as the priority target and minimizing operation costs as the secondary one. The constraints include energy storage operation conditions, etc. For the built model, this paper uses JAS algorithm combined with mixed integer programming with piecewise linearization, and the intelligent single particle algorithm is applied to solve the subsequent mathematical problem. Last, an example is made to verify the proposed model. It comes out that the proposed method can maximize consumptive rate of PV at the same time minimize operation costs in conditions of different PV penetration rate, which makes the model more practical and useful.

energy storage scheduling mode； two-stage optimization； multiple objective； consumption of PV; JAS algorithm; intelligent single particle algorithm

2016-07-05。

國家電網公司總部科技項目 (520201150012)。

李鵬(1965-)，男，教授，主要研究方向為新能源并網發電微網技術、電能質量分析與控制、電力電子技術在智能電網中的應用等,E-mail:ncepulp@gmail.com。

TM615

ADOI:10.3969/j.issn.1672-0792.2016.10.001