一種用于信號估計的改進變步長LMS算法

劉　牮，李　彧

(上海理工大學 光電信息與計算機工程學院,上海200093)

?

一種用于信號估計的改進變步長LMS算法

劉牮，李彧

(上海理工大學 光電信息與計算機工程學院,上海200093)

為了改善現有的變步長LMS自適應算法在對帶有噪聲的信號估計中存在步長調節參數較多、收斂速度慢、不易調節、對噪聲較為敏感等現象，綜合已有的變步長算法提出了一種基于升余弦窗函數與誤差延時相結合的可調節的變步長算法，給出理論分析的同時利用MATLAB建模仿真驗證，表明該算法能進一步提高收斂速度的同時，確保在低信噪比環境下能順利提取期望信號。經過改進的升余弦窗函數可以做到僅調節一個參數即可完成信號估計，驗證的結果表明，該算法在收斂速度與穩態失調上均優于其他變步長算法，具有一定的工程實用價值。

LMS算法；自適應信號估計；變步長；收斂速度；MATLAB

0　引言

信號采樣估計系統中由于引入噪聲導致所估計的結果包含較大的誤差。由于噪聲屬于隨機信號，呈現為分布在全頻段內的隨機信號，這導致了傳統意義上的FIR或其他數字濾波方法，針對特定頻率段信號濾除的功能在對于白噪聲的濾除上無法達到滿意效果。自適應濾波算法可以利用輸入信號與濾波器輸出信號的差值作為反饋來不斷調整濾波器的系數，從而達到理想的濾除噪聲效果。

隨著自適應概念的提出，LMS(Least Mean Square)算法在自適應濾波方面由于工程實現簡單，收斂速度理想，廣泛應用在信號估計、噪聲濾除、系統辨識等領域。自適應算法中收斂速度、穩態失調量、跟蹤速度、穩態誤差是衡量算法優劣的判別因素，其中收斂速度與穩態失調量是最關鍵的兩個因素。傳統LMS算法中收斂步長為固定值，一般是比較小的數，當步長較大時收斂速度較快，能很快地使誤差收斂在一個穩定震蕩的范圍內，這個誤差無法消除[1-2]。當選擇較小的步長時雖然可以使誤差縮小但導致收斂時間大大增加[3]。為了解決這一矛盾，許多改進的算法被提出[4-10]，這些算法基本遵循一個規則，當系統初始工作時誤差較大，應當使用較大的步長因子，隨著時間的增加，系統反饋的誤差逐漸縮小時步長隨之變小，降低系統的收斂速度，進一步減小系統輸出誤差。比較有代表性的變步長是文獻[6-9]提出的基于非線性算法的步長調整。文獻[3]29提出利用sigmoid函數修改步長，但隨著誤差的縮小，該函數在零誤差附近步長變化較為劇烈，容易導致系統輸出震蕩，影響算法精度。文獻[9]654提出的基于指數函數的變步長大大改進了收斂速度，但在噪聲干擾的情況下，多次誤差反饋后噪聲信號仍然保持相關性，對噪聲濾除的效果并不理想。文獻[6,8]95，98針對此現象引入了延遲因子，較好地修正了噪聲對信號估計的影響，但由于引入了較大的延時使其收斂速度有所降低。文獻[7,10]1824,2336提出的改進算法兼顧了較快的收斂速度與保持低信噪比下較小的穩態誤差，但引入的步長函數所涉及的參數較多，給系統的調試帶來了不便。

綜上所述，本文在現有的步長調整原則下，提出了一種基于升余弦窗函數的步長調整算法。該算法能改善sigmoid函數收斂速度的同時，同樣能滿足低信噪比下對包含噪聲的信號的估計，同時減少了調整參數，更加便于工程實踐。

1　LMS信號估計的原理及其改進

1.1LMS算法原理分析

引入帶噪聲信號估計的模型，該模型圖如圖1所示。

圖1　LMS算法估計帶噪信號模型圖

該模型中S為待估計信號，N為噪聲，D為延時單元，FIR為自適應濾波器，O為輸出，輸出為期望信號中包含的噪聲的最優估計，實際上是對期望信號中的噪聲做最優估計，誤差e(n)對FIR濾波器的系數進行自動調節。將輸入的信號(期望信號與噪聲的疊加)減去輸出即可得到所估計的不含噪聲的信號。

LMS算法是基于遞推梯度下降的方法，尋找誤差最小化的最優方程解，從而得出FIR濾波器各階系數，其迭代公式如下：

(1)

(2)

(3)

式中：W是濾波器的權系數向量，通常濾波器選擇FIR型濾波器，因為FIR濾波器為穩定系統，并且可以保證線性相位。e(n)是誤差，用于反饋調節濾波器系數；d(n)是期望信號，用于和濾波器輸出做差；μ就是步長因子，LMS算法要求μ的取值為：

(4)

該處Px為：

(5)

式中：N為采樣點數；M為濾波器階數。由式(1)和式(2)得：

(6)

式中：e(n)是與輸入信號有關的誤差。該誤差在圖1所示的系統中代表了對噪聲的估計。將理想d(n)表示為[11]：

(7)

式中：W*為理想濾波器系數；e*為理想估計下的噪聲信號。假設：

(8)

表示濾波器真實系數與理想系數的偏差，式(7)減去式(6)，再對e(n)求平方得：

(9)

當引入e(n)e(n-1)[6]96作為步長調節因子時：

(10)

由于延時后導致X(n)和e*(n)不相關[12]，則對式(10)兩邊取期望得：

(11)

由于輸入噪聲為隨機白噪聲，對于延遲一個單位的白噪聲來說，已經變為不相關信號，所以在使用e(n)e(n-1)代入計算步長因子時，已經可以起到噪聲抑制的作用，從而估計出原始信號[8]98。

由上述分析可以得知，為了在有噪聲環境下提取希望信號，必須加入一定的延時，針對白噪聲的情況下，施加一個單位延時即可。

1.2LMS算法改進

基于文獻[3]28所提出的步長因子變化準則以及之前所分析的引入一定延時的誤差乘積作為步長因子調整的輸入參數[13-14]，現提出基于升余弦窗的步長變化函數：

(12)

升余弦窗函數是為了減小采樣序列中頻譜泄露而引入的截斷采樣序列的函數，是一種邊緣滾降平緩，并且具有比指數函數更加陡峭的衰減特性。該特性可以滿足步長因子變化的準則，分析式(12)隨著參數的變化，當α取0.7，β分別取不同的值時μ(n)的變化。

圖2為β分別取512、256、128、64時的升余弦窗函數的波形圖，在MATLAB中繪圖時將迭代次數設置為64次。

圖2　α=0.7 時不同β下的步長變化曲線

從圖2中可以看出，在迭代次數不變的情況下，β的值可以調節曲線的衰減程度，當迭代次數固定，β值增大時，曲線衰減程度降低，如果β遠遠大于迭代次數時，在迭代次數范圍內觀察步長曲線時有可能會導致迭代完畢后仍然無法使e(n)收斂，造成算法失調。當迭代次數固定，β值逐漸減小時，可以觀察出步長因子曲線衰減程度逐漸增加，當β減小至于迭代點數相同時呈現標準升余弦窗函數圖形，該β值為臨界值，如果繼續減小β，則可能導致在步長因子調整的過程中違背其變化準則，出現大幅度震蕩或不收斂的情況。β的取值推導過程如下，對濾波器權系數公式(3)兩邊取數學期望得：

(13)

式中：W*為濾波器最佳系數的維納解；R為輸入信號的自相關矩陣E[X(n)XT(n)]。對于該矩陣可以轉換為對角矩陣與其正交特征向量的乘積，為了使得LMS算法收斂，μ的值應該滿足如下條件

(14)

(15)

此處，K為迭代次數，當滿足以上條件時，調節β值可獲得較滿意的收斂速度。

針對β值不變的情況，不同的α值會對步長因子曲線帶來影響，選取迭代次數為64次，當β取128時，不同的α對步長因子曲線的影響如圖3。

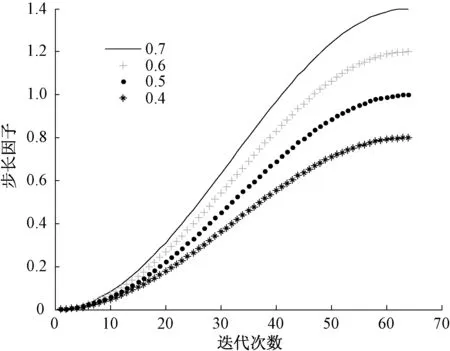
圖3　β=128 時不同的α下步長變化曲線

從圖3中可以看出，當α為0.7時，具有最大衰減程度的步長變化曲線，圖3中的4條曲線均滿足步長因子變化趨勢，隨著迭代次數的增多，誤差逐漸縮小趨向于零。α=0.7時，此時誤差最大，表示具有1.4的誤差，由于在含噪聲信號的估計中多次迭代的誤差均為比較小的數，因此選定一個合適的α值后一般不需要再次調整，在本文所提到的信號估計系統中，多次迭代的誤差均小于1。為穩妥起見，可將該值設為0.7，如在實際測試過程中發現無法收斂時，調節該參數。

經過以上分析可以發現α和β都能起到調節步長因子的作用，相對于α來講，β的調節范圍更廣，可以理解為β屬于粗調整，α屬于細微調整，系統初次調試時可以將α設置為稍大一些的值，在帶噪信號估計的工程實踐中甚至可以固定使α=0.7，僅調節β即可獲得滿意的收斂效果。

2　算法對比

為對比本文算法與其他算法在收斂速度與均方誤差上的性能，在MATLAB下設計程序，輸入信號為零均值，方差為1的高斯白噪聲，此處僅僅測試對于輸入高斯白噪聲，輸出跟隨輸入未知系統時的收斂速度與均方誤差，本次測試使用未知系統加權系數為[0.8，0.3]，迭代次數為2 000次，如圖4～7所示。針對之前分析，同時給出了不同α與β值的步長曲線與均方誤差值來驗證之前的分析。從圖4到圖7中可以看出，α較大，β值較小的時候，此時升余弦窗的滾降趨勢增大，LMS算法趨向于更快的收斂速度，更迅速地收斂于均方誤差最小值。快速收斂的同時為了減小穩態失調，步長因子開始變化趨緩滿足之前所討論的收斂原則。

圖4　α=0.7，β=20本文算法 2 000次迭代的步長因子曲線

以下為對比文獻的算法曲線。圖8，圖9為文獻[3]29的不延時計算誤差算法的步長曲線與均方誤差曲線。圖10、圖11為文獻[8]98的有延時計算誤差算法的步長曲線與均方誤差曲線。從圖8至圖11可以看出，具有延時的誤差所導出的步長能更快速收斂的同時，對于噪聲的剔除更理想，亦即對噪聲更不敏感，其步長因子在多次迭代后相比于無延時誤差的步長逐漸趨于穩定。而本文的算法能綜合兩者的優點，快速收斂的同時具有更小的穩態失調量。

圖5　α=0.7，β=20本文算法 2 000次迭代均方誤差曲線

圖6　α=0.1，β=32本文算法2 000次迭代的步長因子曲線

圖7　α=0.1，β=32本文算法 2，000次迭代均方誤差曲線

圖8　2 000次迭代誤差不延時算法的步長曲線

圖9　2 000次迭代誤差不延時算法的均方誤差曲線

圖10　2 000次迭代誤差延時一個單位算法的步長曲線

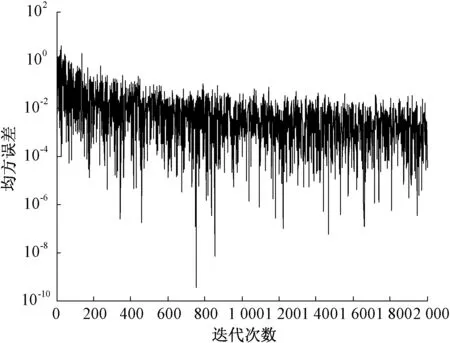
圖11　2 000次迭代誤差延時一個單位算法的均方誤差曲線

3　算法應用于帶噪信號估計的計算機仿真

在MATLAB下創建純凈正弦信號，s=sin(2πt/10)，疊加高斯白噪聲，信噪比為10(低信噪比)，延遲單元D設為延遲100，濾波器選用FIR，32階加權系數，輸入為受噪聲污染的正弦信號，輸出為降噪后的估計信號，經由MATLAB按照圖1模型，并使用升余弦窗函數作為步長調節函數，α=0.7，β=14，仿真程序運行結果如圖12。

圖12(a)表示在MATLAB下仿真出的疊加了污染信號(高斯白噪聲)的波形；圖12(b)表示所疊加的污染信號，均值為零，方差為1的高斯白噪聲信號；圖12(c)表示未疊加高斯白噪聲的正弦信號；圖12(d)表示通過LMS降噪模型(圖1)后輸出的正弦信號，可以明顯地觀察到噪聲信號已經被有效抑制；圖12(e)表示使用升余弦窗變步長算法的均方誤差(學習)曲線。通過圖中實際濾波信號與帶噪信號的對比，可以明顯看出噪聲信號被極大地抑制，證明通過升余弦窗調節的可變步長LMS算法能夠滿足帶噪信號的估計。

4　結論

針對不同變步長調節方法，綜合考慮后引入一種方便可行，參數較少的變步長函數，在保證能將低信噪比的信號較好地提取出來的同時進一步加快收斂速度，同時簡化參數，本文中的算法可以較快地調整出滿意的效果，大多情況下根據實際情況僅僅調節一個β值即可滿足要求，而且可以利用在DSP平臺上的數字濾波窗函數[15]，節省硬件資源，操作簡便，具有較廣闊的應用前景。

圖12　整體濾波效果圖

[1]曹景升, 單毅, 樊雪濤. 自適應濾波器在噪聲處理中的應用[J]. 電子技術與軟件工程, 2015(7):129.

[2]鄭顧平, 杜向楠. 基于LMS自適應濾波的零序電流去噪研究與實現[J]. 電力科學與工程, 2011, 27(12):27-31.

[3]陳泳, 田金鵬, 劉燕平. 一種新的變步長LMS自適應濾波算法[J]. 電子測量技術, 2015, 38(4):27-31.

[4]王洪誠, 王蕾, 沈霞,等. 基于改進增益型自適應LMS算法的諧波檢測方法[J]. 電力系統保護與控制, 2016, 44(5):42-46.

[5]張炳婷, 趙建平, 劉鳳霞. 一種改進的可變步長LMS算法及性能分析[J]. 通信技術, 2015, 48(11):1217-1221.

[6]還秋云, 邱曉暉, 劉曉飛. 引用范數的雙曲正切函數變步長LMS算法[J]. 信號處理, 2014, 30(1):93-99.

[7]張紅梅, 韓萬剛. 一種新的變步長LMS自適應濾波算法研究及其應用[J]. 儀器儀表學報, 2015, 36(8):1822-1830.

[8]李梁, 庹先國, 李懷良,等. 一種改進的自適應濾波算法在微震信號處理中的實現[J]. 中國測試, 2015, 41(1):97-99,119.

[9]張炳婷, 趙建平, 馬淑麗. 新的變步長LMS算法在系統辨識中的應用[J]. 通信技術, 2015, 48(6):653-656.

[10]郭瑞, 李寶華, 馬奧運. 一種基于改進雙曲正切函數的變步長自適應濾波算法[J]. 計算機應用研究, 2015, 32(8):2335-2338.

[11]陳立偉, 譚志良, 崔立東. 改進的LMS算法在噪聲對消中的應用[J]. 無線電工程, 2015(6):70-73.

[12]英格爾. 數字信號處理 (MATLAB版)[M]. 西安:西安交通大學出版社, 2008.

[13]張紅梅, 韓萬剛. FIR濾波器時延分析及其在信號融合中的應用[J]. 武漢大學學報(工學版), 2016,49(2):303-308.

[14]董胡. 基于窗函數與MATLAB的數字FIR濾波器設計[J]. 微型電腦應用, 2016(3):30-32.

[15]郭璐, 黃鶴, 杜凱,等. DSP環境下新的變步長LMS自適應濾波算法[J]. 電子設計工程, 2016(1):135-137.

An Improved Variable Step Size LMS Algorithm for Signal Eestimation

LIU Jian, LI Yu

(School of Optical-electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China )

In order to improve the performance of the existing variable step-size LMS algorithm during signal estimation with the problems such as too many parameters, rather slow convergence speed, relatively difficult to adjust, and quite sensitive to noise, a new variable step-size algorithm combining raised cosine windows function and delay error was proposed based on the existing one. The theoretical analysis and the simulation in MATLAB are given in this paper. The proposed algorithm can not only improve the convergence speed but also ensure the desired signal be extracted successfully in low SNR environment. The improved raised cosine windows function can help LMS algorithm estimate the signal with only one parameter, and the results show that the algorithm is superior to other variable step-size algorithms in both convergence speed and steady state, and it also is of certain engineering and practical value.

LMS algorithm; adaptive signal estimation; variable step-size; convergence speed; MATLAB

2016-06-04。

上海市科技英才揚帆計劃項目(15YF1408300)。

劉牮(1961-)，男，副教授，主要研究方向為電子技術及嵌入式技術應用，E-mail：liuliu2702@163.com。

TN911.7； TH701

ADOI:10.3969/j.issn.1672-0792.2016.10.004