國內外高層次（數學）思維研究述評

常 磊

?

國內外高層次（數學）思維研究述評

常 磊

（華東師范大學數學系，上海 200241）

高層次思維是近年來教育研究的熱點問題之一，主要集中在概念的界定，具體學科中的高層次思維能力的教學和測評等方面．其概念存在多種具有較高認可度的界定，且存在顯著差異；其教學研究涉及教學的諸多方面，且呈現與新技術相結合的趨勢；其測評研究正在積極地建設和完善．這些研究為推進中國高層次數學思維的理論研究與實踐探索的啟示包括：加強高層次數學思維的界定研究；加大實證研究力度，探索高層次數學思維能力教學的有效實施；建立科學的高層次數學思維能力測評體系．

高層次（數學）思維；界定；教學；測評

國外的很多教育研究者認為[1~4]，高層次思維能力（Higher Order Thinking Skill，簡稱HOTS）是人生成功的一個重要因素．不斷變化和充滿挑戰的世界需要我們的學生，具備超越構建知識的能力，即需要高層次思維能力．近年來，發展和加強學生的高層次思維能力在國際上已經成為了一個主要的教育目標[5]．在數學教育研究領域，為了避免很多國家把能力培養退化為一些低層次的、以記憶為主的模仿活動帶來的負面影響，西方研究者提出了高層次數學思維能力的概念[6]，并認為數學教學的目的是培養學生透過學習數學知識發展高層次思維能力[7]．鄭毓信也提出：數學思維的現代研究，特別是“高層次數學思維研究”，已為解決許多重大數學教育理論問題提供了重要啟示[8]．從高層次思維的界定、高層次（數學）思維能力的教學、高層次（數學）思維能力的測評幾個方面入手，梳理國內外學者相關的研究成果，以期為今后國內的高層次數學思維研究提供有益的借鑒，引發更深層次的探索．

1 高層次思維的界定

已有的文獻資料中關于高層次思維的界定差異比較大，主要有以下幾類．

1.1 以布魯姆分類學為基礎的高層次思維界定

1956年，美國教育心理學家布魯姆（Benjamin S. Bloom）把認知領域的教育目標由低到高分為識記、領會、應用、分析、綜合和評價6個層次[9]．高層次思維的研究起源于布魯姆和加涅（Robert M. Gagne）等人的學習理論，很多研究者認為認知思維層次符合布魯姆分類學，將識記、理解、應用視為低層次思維，分析、綜合和評價視為高層次思維．2001年，布魯姆的學生Anderson等人對布魯姆分類學進行了修訂[10]，認知水平按照復雜程度遞增原則依次分為記憶、理解、應用、分析、評價、創造．類似的，后3個認知水平“分析、評價、創造”被視為高層次思維．

1991年，顧泠沅領導的青浦實驗小組，對布魯姆分類學等進行重新認定，并在大樣本測量數據的基礎上構建了數學認知水平分析框架[11]．學生的數學認知水平被分為較低與較高兩個范疇，每個范疇分為兩個層次，較低認知水平范疇分為計算與概念兩個層次，分屬操作性和概念性記憶水平；較高認知水平范疇分為領會與分析兩個層次，分屬說明性理解和探究性理解水平．

1.2 Resnick對高層次思維的界定

布魯姆等人認為，高層次思維是建立在低層次思維或基本技能之上的，并且二者有著明確的界限區別．然而，一批有影響力的研究者認為思維是整體的、不可明顯分層的，他們對依據布魯姆分類學對思維層次進行簡單分層提出了質疑．1987年，美國國家研究委員會所屬的數學、科學、和技術教育研究委員會發表了一份研究報告[12]，試圖整合所有關于高層次思維的理論，為培養學生的高層次思維能力提出建議．該項研究的主要負責人Resnick認為高層次思維這個術語抵制精確形式的定義，因為它的一些關鍵特征無法定義得非常準確，但是當高層次思維能力在實踐中發生時卻能夠被識別出來．這項研究最終只把高層次思維描述為具備或者包括以下幾個特征（見表1）．

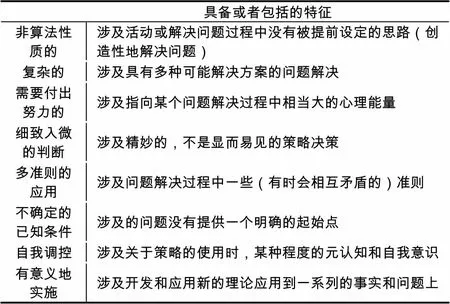
表1 高層次思維具備或者包括的特征

1.3 從心理學或認知科學視角對高層次思維界定

Lewis和Smith從心理學的視角對高層次思維的定義是[13]：高層次思維發生在，當個體需要將新知識和已有知識建立聯系，或者改變及拓展這些知識來達到一個復雜的認知目的或者在復雜的情境中發現可能的答案．低層次思維僅僅需要對信息進行常規或機械化的應用，而高層次思維挑戰學生的解釋、分析和使用信息解決問題方面．以類似的視角，中國臺灣的葉玉珠認為[14]，高層次思維涉及個體主動處理一連串的心理過程以達成做判斷、決策、解決問題、建構及溝通意義的能力和意愿．在這些心理過程中，個體必須視情境而定，適當地選擇、結合和運用其相關的知識與技巧，并隨時監控和調節其思維．

美國芝加哥大學的Richland和Simms從認知科學的角度，把高層次思維定義為關系結構映射（relational structure mapping）過程，將學科信息看作系統關系，調整和比較/對比這些系統，以發展更高層次的關系（如相同、不同、或因果關系），然后基于這些高層次關系得出結論、解決問題和推理[15]．

1.4 復雜思維集合論

還有一類觀點認為高層次思維是一個由多種復雜思維所構成的思維集合．這個集合可能包括批判性思維（再）創造性思維、直覺思維、發散思維、反思思維、元認知思維等[16~19]．

1.5 高層次數學思維的界定

美國全國數學教師理事會（NCTM）1989年把高層次思維描述為解決非常規問題時需要的思維[20]．非常規問題是指有一個或多個適當的解決方案未被學生提前知曉的問題，當人由于需要解答某個不能通過對學過的知識的常規應用解決的問題，必須要對信息做出詮釋、分析或處理時對大腦的挑戰性和拓展性使用[21]．

中國的周超以思維品質為視角，在林崇德先生對思維品質研究的基礎上，分別從深刻性、靈活性、獨造性、批判性與敏捷性界定了數學高層次思維[22]．她認為不同的思維形式之間并沒有高低之分，不能根據思維的形式來區分思維層次．

塞浦路斯大學教育學院的兩位學者基于整體化思維模型，認為高層次數學思維是一個廣義術語，其可操作型定義整合了基本數學知識、批判性思維、創造性思維和各種復雜的思維過程，這種定義利于開展高層次數學思維測試和設計有效的學習環境發展這種思維[23]．

總體來看，目前關于高層次思維存在多種具有較高認可度的界定，這些解釋基于不同的理念，因此存在顯著差異．依據布魯姆分類學對高層次思維的界定比較清晰、簡單，對于一線教師更加容易接受、理解和執行，在測評中便于出題、施測、評分和報告結果，缺點是對高層次思維的劃分有些過于簡單、人為設定的特征明顯，不夠準確和全面，缺少科學扎實的實證研究支撐．Resnick等對于高層次思維的界定理論研究性較強，對高層次思維的特征分析比較全面深刻，是目前被認可度最高的一種界定，但因其缺少可供實際教學和測評的框架，對于一線教師顯得實用性不足．美國全國數學教師理事會和Newmann等研究者從問題解決類型的角度來區分學生是否使用了高層次思維，便于一線教師判斷和測評，但對高層次思維的內涵并沒有給出科學全面的分析．Lewis和Smith等人從心理學視角分析，專業性較強，普通研究者和教師難以理解和操作．思維集合的觀點具有特殊性，關注了某些復雜的特殊思維，使一線教師容易開展對特殊思維的專項訓練與測評，但缺乏對高層次思維的統領認識和全面把握．發展高層次數學思維的重要性已經得到了廣泛認可，但針對高層次數學思維的界定研究視角化特征明顯，需要在高層次思維界定研究的基礎上更加全面和完善．

2 高層次（數學）思維能力的教學

在過去的幾十年里，研究者已經發現，高層次思維能力是可以被教、培養和發展的．在課堂教學中，培養學生的高層次思維能力是重要任務，也是課堂教學的重點問題[24]．高層次（數學）思維的教學研究主要可以分為課程標準與文化，教學模式、原則和策略，教學載體，教學與信息技術的使用幾個大的方面．

2.1 課程標準和文化與高層次（數學）思維

從國際上看，作為主要的發達國家，英國和美國都非常強調高層次思維教學在學校課程中的重要性．

美國的2010年版《共同核心州立標準》強調積極發展學生的高層次數學思維，清楚地提供了學生需要學習的具體技能，并要求教師為學生提供參與高層次任務和回答高層次思維問題的機會[25]．有研究者使用韋伯的深度知識分析框架，發現美國2009年版新澤西州的課程標準比較2010年版《共同核心州立標準》，對高層次數學思維的要求更高[26]．

英國威爾士議會政府2011年發布了一份名為《發展高層次數學思維能力》的指導手冊，主要用于提高K3至K4階段（中學）學生在GCSE和 PISA測試中的表現[27]．手冊中包括了具有高層次思維特征的學生作業案例，每個案例都是學生對于教學任務的真實反饋，配有確定其對應思維層次特征的評論．

從國內的研究看，李瓊等研究發現：與使用原課程的學生相比，使用新課程的小學生在高層次思維能力方面表現出明顯優勢[28]．張曉斌發現，中國《普通高中數學課程標準﹙實驗﹚》對培養思維能力的思維過程做了10個方面的方向性要求，但沒有對思維層次做出具體規定，建議制定出量化的具有可操作性的數學思維能力目標[29]．

Yeung和Shirley認為文化因素被認為在確定教學方法方面起到重要的作用[30]．他們對12名中國香港教師進行深度訪談，檢測他們對于有效高層次思維教學的觀念，并將之與西方教學理論和中國傳統的教學價值進行了對比，并揭示了中國的價值觀，主要是儒家思想，是如何影響香港教師關于有效高層次思維教學的認識的．

2.2 高層次（數學）思維的教學模式和原則及策略

關于高層次思維能力的教學模式，歸納起來共3類[31]：其一，獨立課程模式，強調思維能力的專門、直接教學，將思維能力的教學獨立于具體學科課程之外；其二，內容模式，認為某些認知技能是特定存在于具體學科的，如數學或科學，應該在具體的學科背景下進行教授；其三，注入模式，即將思維能力的教學與課程的教學融合在一起，不拘泥于某些特殊的思維策略和技能的教學．

Weiss認為，促進高層次思維能力的發展應該遵循以下標準[32]：（1）學生應該把學習的重心由知識轉變成理解；（2）教師應該為學生創造一個能夠有效互動的交流環境，鼓勵他們驗證、質疑、批判以及評估其它因素，通過各種途徑參與構建知識，并通過自我探索生成新的知識；（3）學生需要意識到，他們必須成為一名積極的學習者，積極主動學習，對自己的學習擔起責任．

Caine等研究者撰寫了《12條大腦的學習原則——發展高層次思維和執行能力的教學》[33]，提出了一些有效的教學原則，例如：采用吸引學生學習的策略，建立基本的學習技能；學習過程引入同伴指導；反思問題和列出評價清單；應用現實生活中的例子解釋大腦協調學習行為等．

美國佛羅里達州立大學的學習與評價促進中心繪制了一幅描述高層次思維能力發展過程框架圖（如圖1），并從理論上對于高層次思維能力的發展過程及各個要素之間的關系進行剖析，為高層次思維的教學提供了思路和方法[17]．

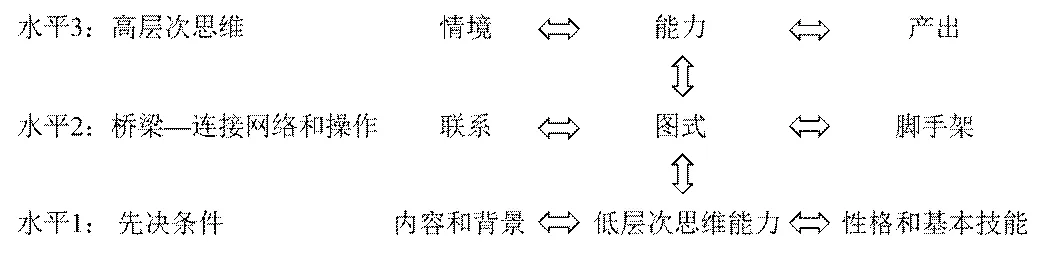
圖1 高層次思維能力發展過程框架圖

美國匹茲堡大學的學習研究與發展中心（LRDC）開展過一項名為QUASAR的中小學數學教育改革項目[34]．項目負責人Stein等人在Resnick的高層次思維特征研究的基礎上提出了培養高層次數學思維能力的高水平認知數學任務特征和數學任務設計，在此基礎上，他們還研究得出保持高認知要求水平的7條策略．

Budsankom等研究者應用元分析結構方程模型，基于166項實證研究，得出教室環境、學生的心理和智力特征對高層次思維能力有直接影響，家庭特征本身對高層次思維的影響甚微，但可以通過心理特征對高層次思維產生間接影響[35]．

2.3 高層次（數學）思維的教學載體

著名的數學家和數學教育家波利亞提出[37]：教師在課堂上使用非常規問題的教學策略，可以在理解、探究和應用數學概念的過程中為所有學生提供培養高層次思維能力的機會．具有非常規性、情境性、開放性特征的高認知水平數學教學任務有助于發展學生高層次思維能力[38~39]．

戴再平認為：數學開放題的教學有助于培養學生的高層次數學思維[40]．含有開放性問題的數學探究活動，條件開放、方向不明、結論未知，有利于學生高層次思維能力的發展，但由于高層次思維對于不同學生是相對的，任意某個開放性問題不會激發所有學生的高層次數學思維[41]．

基于問題的學習（PBL）模型同樣被認為是發展學生高層次思維的有效方式．以色列研究者提出一種方法來組織基于問題的學習，發展學生的高層次思維能力[42]．這種方法通過一個包含兩個階段的基于問題的學習過程，包括了具體步驟和實施過程，具有較強的可操作性．

加拿大研究者針對數學建模活動設計了一種模型誘發行為（Model Eliciting Activity），通過學生在數學建模活動中的描述、解釋、判斷和表現明確揭示他們的思維過程．研究還討論了“假使……將會怎么樣?”如何拓展學生的數學思維并且通過改變問題的條件，從而改變解決方案，最終支持學生發展高層次數學思維[43]．

美國研究者做了一項關于發展性數學方法課程培養小學生高層次思維的實證研究[44]，設計了實驗組和對照組，以數學問題解決、創造性思維為主要測試內容開展了前后測．結果表明，發展性數學方法課程對于培養小學生的問題解決能力、創造性思維能力為主的高層次思維能力是有效的．

澳大利亞研究者與九年級數學教師合作，在不同的語言設置下，分析學生的任務解決案例，結合文獻研究，開發了高層次數學思維實踐中的語言要求框架[45]．框架中包括了4個分類：概括的語言、比較的語言、比例推理的語言、分析影響的語言．他們描述了4類語言的要求，分析和揭示了學生在參與這些高層次數學思維任務時面臨的語言挑戰．

關于中國的課堂教學，季素月指出中國數學課堂教學存在不利于培養學生高層次思維的缺點[36]：以片面追求考試成績為目的，高密度、低認知水平的課堂教師提問和大容量、重復式的習題訓練不能甚至限制學生的高層次數學思維發展．

2.4 高層次（數學）思維教學與信息技術的使用

潘巧明認為計算機技術可以使數學教育有足夠多的時間在高層次思維水平上進行，但也要防止過分依賴媒體視覺化的效果，影響思維的深度[46]．

Susanti探討了計算機輔助現實數學教育對學生高層次思維能力的影響，并與純粹的現實數學教育進行了對比，實驗研究結果表明：（1）計算機輔助現實數學教育相比純粹現實數學教育，學生的高層次思維能力成績存在差異；（2）計算機輔助現實數學教育相比純粹現實數學教育，學生的高層次思維能力的提高沒有差異[47]．

Collins和Knoetze闡述了使用教育技術作為認知工具的學習環境促進高層次思維能力發展的猜測和原則[48]．這些猜測和原則分為7個相關的集群，它們之間協調作用可以促進發展學生所需的高層次思維能力．

依靠智能網絡技術支撐的在線大學教育課程MOOCs是近年來國際教育發展的熱點之一，Xu Wang等研究者基于MOOCs學習背景下，探索了參與高層次思維的討論行為相比僅僅關注課程學習材料對于學習MOOCs課程的影響[49]．

對文獻梳理后可以看出，關于高層次思維能力教學的研究，早期主要偏重于理論建構，近年來，國際上出現了很多實證研究和案例研究．研究的學科領域涉及幼兒教育，中小學數學、科學、藝術和大學的工程、經濟、醫學教育等學科．大多數高層次（數學）思維能力教學研究是基于布魯姆分類學理論或Resnick的高層次思維特征研究而進行的，少部分偏重于某些特殊的復雜的思維能力的教學研究，譬如批判性思維能力（再）創造性思維能力等．在主要發達國家的引領下，世界上很多國家的中小學課程標準都對高層次思維教學提出了要求，中國的中小學課程標準應對高層次思維作出更具體細致的要求．國外關于高層次（數學）思維的教學模式、原則和策略研究比較詳實，國內相關的研究則凸顯不足．關于高層次思維教學的載體有多種，基本上都是以高認知水平任務和問題為導向，輔助高認知水平的活動和語言．隨著教育技術的飛速發展，與教育技術結合的高層次思維教學研究也逐漸增多．國內以高層次數學思維教學為主題的的研究比較少，相關研究散見于其它主題的研究中，譬如，數學課堂合作學習應促進學生高層次思維參與[50~51]．

3 高層次（數學）思維能力的測評

思維能力的測評始終是國際研究的熱點和難點，高層次思維能力由于其復雜性、深刻性、開放性的特點，對其準確測評的難度更大．國際上關于高層次（數學）思維能力的測評的研究主要分為理論研究和實證研究兩大類．

3.1 高層次（數學）思維能力測評的理論研究

Brookhart介紹了測評高層次思維的一般原則，認為高層次思維能力的測量要求提供給學生不熟悉的問題或任務，并且學生有足夠的先驗知識使他們能夠應用高層次思維能力回答或解決問題[52]．

Newmann等制定了一個高層次思維的課堂測評量規[53]，如表2所示．該量規用來量化測評課堂教學中高層次思維參與的程度，評價標準比較合理，邁出了科學測評課堂上學生參與高層次思維的重要一步．

表2 高層次思維的課堂測評量規

Kulm等探討了中小學高層次數學思維測評的理論、研究、實踐和規則，闡述了高層次數學思維評價的目標和測試標準[54]．

鮑建生認為考查學生如何從低層次數學思維過渡到高層次數學思維的工作主要有兩個途徑[55]：一是滲透到具體的數學概念學習上，考察學生的數學思維是如何發展的；二是利用認知單元和認知根源等概念在宏觀上討論數學認知的發展．

范良火提倡[56]，中小學數學外部測試應增加能反映學生高層次數學思維能力的試題，適當延長學生考試的時間，適當使用計算器等．對于內部測評，可以采用多元測評方法測評學生高層次數學思維能力．這項研究對中國地區性的中考具有借鑒意義．

還有國內研究者對當前的國內某些課堂評價策略提出了批評，認為它們不能測評高層次思維[57]．傳統數學測評側重低層次思維，而不是高層次思維，強調對題目的即時反應而不是創造思維和表達[58]．

3.2 高層次（數學）思維能力測評的案例或實證研究

Thompson在一項案例研究中發現[59]：（1）學生對于解答測試題的算法或方法以及問題情境的熟悉與否對于判定試題屬于高層次思維還是低層次思維很重要；（2）在設計測試題時，使用一個具有有限分類的數學學科的評價框架很重要；（3）包含現實情境測試題不是必然需要學生運用高層次思維．Thompson的研究可以為課堂測評或者大規模測評中關于高層次思維測試題的編寫提供參考．

“高層次思維測評筆試試題”[60]為想要測量高層次思維能力而編制測試題的教師提供了參考，對如何編制多項選擇和建構反應題（constructed-response items）、表現性評價任務以及認知、情感和精神活動3個領域的“檔案袋”評價法給出了指導，還提供了試題修訂和試題答案統計分析的流程．

TIMSS和PISA已經成為世界上具有重要影響力的國際教育成就測試項目．一些研究者認同TIMSS和PISA測試可以測評學生的高層次數學思維能力，并提出要采取以加強學生的高層次思維能力為途徑提高本國學生在TIMSS和PISA測試中的表現[61]，但是也有另一些研究者認為TIMSS和PISA難以測評學生的高層次數學思維能力[62~64]，原因主要是大多數測試題采用了用于測試程序性知識和常規問題解決技能的多項選擇題的形式．

學生高層次思維能力的發展與解決數學問題時的思維過程密切相關．Bakry和Bakar的實證研究結果顯示，數學能力高的學生能夠創建意義、提出觀點和得出結論；中等數學能力的學生能夠創建意義、提出觀點但不能得出結論；數學能力較低的學生不能夠創建意義、不能得出結論[65]．

Agus Budiman采用了Borg和Gall的測評工具開發模型，研制了一個高層次數學思維能力的測評工具，并測量了八年級學生的高層次數學思維能力．該測評工具由24個多項選擇題和19個問答題組成．經過多項技術指標檢測，該測評工具被認定為有效和可靠的[66]．

從以上梳理結果來看，關于高層次（數學）思維能力的測評研究成果頗多，涉及測評途徑、測評原則、測評量規、測評方法方式、測評試題編制、測評的有效性等，但其中存在的爭議也很大．大多數研究者都認同亟需改革目前已有的中小學數學能力測評體系，需要設計出一套適應高層次（數學）思維能力的、幾乎完全不同于傳統的數學思維能力測評體系，但是目前關于高層次（數學）思維能力測評的大部分研究還缺乏充足的實證研究支撐，面臨著許多客觀環境條件的制約，需要在對高層次（數學）思維的內涵和外延進行清晰界定的基礎上，結合詳實可靠的數據或案例支撐，構建高層次（數學）思維能力測評體系．

4 結 語

中國的高層次思維研究起步較晚，相關主題的研究數量比較少，目前可查到的僅有3篇碩士論文，以及幾十篇的期刊論文，但是呈現出逐漸增多的發展趨勢．與國際上的相關研究相比較，中國的高層次思維和高層次數學思維研究中理論研究還比較少，且都是關于高層次數學思維的界定方面，關于高層次思維的教學和測評方面的理論研究缺乏深度，結合具體學科的實證研究也不多，一些實證研究缺少詳實可靠的數據支撐．經過對國內外相關研究成果的梳理可以得出的啟示包括：加強高層次數學思維的界定研究，在國外研究成果的基礎上，結合國內數學教育教學的優秀理論和實踐，得出更加科學全面、方便理解、具備可操作性的界定；加強實證研究的深度和廣度，結合詳實準確的數據，或者具體的真實案例，探索高層次數學思維能力教學的有效實施；參考國外研究成果，基于國內的教育教學實情，結合具體學科特點，探索建立和完善有效的高層次數學思維能力測評體系．

［參考文獻］

[1] Stein M K, Henningsen M. Building Student Capacity for Mathematical Thinking and Reasoning: An Analysis of Mathematical Tasks Used in Reform Classrooms [J]., 1996, 33(2): 455-488.

[2] Hiebert J, Others A.[M]. Heinemann, 1997.

[3] Costa A L E.[M]. Association for Supervision and Curriculum Development, 2001.

[4] Saavedra AR, Opfer VD. Learning 21st-Century Skills Requires 21st-Century Teaching [J]., 2012, 94(2): 8-13.

[5] Zohar A, Schwartzer N. Assessing Teachers’ Pedagogical Knowledge in the Context of Teaching Higher-Order Thinking [J]., 2005, 27(13): 1?595-1?620.

[6] 鮑建生．關于數學能力的幾點思考[J]．人民教育，2014，（5）：48-51．

[7] Romberg T A, Collis K F, Zarinnia E A.[M]. National Center for Research in Mathematical Sciences Education, 1989.

[8] 鄭毓信．“高潮”之后的必要反思——從理論研究的角度看[J]．數學教育學報，2010，19（1）：1-5．

[9] Bloom B S, Englehart M, Furst E, et al.[M]. David McKay, 1956.

[10] ?Anderson L W, Krathwohl D R, Bloom B S.[M]. Allyn & Bacon, 2001.

[11] 青浦實驗小組．學會教學[M]．北京：人民教育出版社，1991．

[12] ?Resnick L B.[M]. National Academy Press, 1987.

[13] ?Lewis A, Smith D. Defining Higher Order Thinking [J]., 1993, 32(3): 131-137.

[14] 葉玉珠．高層次思考教學設計的要素分析[J]．國立中山大學通識教育學報（臺灣），2002，（1）：75-101．

[15] ?Richland, Lindsey Engle, Nina Simms. Analogy, Higher Order Thinking, and Education [J]., 2005, 6(2): 177-192.

[16] 克魯捷茨基．中小學數學能力心理學[M]．李伯黍，洪寶林譯．上海：上海教育出版社，1983．

[17] ?King F J, Goodson L, Rohani F.[M]. Center for Advancement of Learning and Assessment, Florida State University, 1998.

[18] 劉儒德．基于問題學習對教學改革的啟示[J]．教育研究，2002，（2）：73-77．

[19] 張定強，趙宏淵．論數學反思能力[J]．課程·教材·教法，2005，（3）：49-54.

[20] ?National Council of Teachers of Mathematics.[M]. NCTM, 1989.

[21] Newmann F M. Promoting Higher Order Thinking in Social Studies: Overview of a Study of 16 High School Departments [J]., 1991, 19(4): 324-340.

[22] 周超．數學高層次思維的界定及評價研究[D]．蘇州大學，2003．

[23] ?Sophocleous P, Pitta-Pantazi D.s [C]. The 9th Mathematical Creativity And Giftedness, Romania, 2015．

[24] 孔企平．關于評價與教學過程有機結合的探索[J]．全球教育展望，2014，（12）：18-24．

[25] ?Common Core State Standards Initiative.[M]. Washington, DC: National Governors Association Center for Best Practices and the Council of Chief State School Officers, 2010.

[26] ?Sforza D, East Rutherford NJ, Tienken CH, et al. A Comparison of Higher-Order Thinking Between the Common Core State Standards and the 2009 New Jersey Content Standards in High School [J]., 2016, 12(4): 5-31.

[27] ?Welsh Assembly Government (Wales). Developing Higher-order Mathematical Skills [EB/OL]. http://dera.ioe.ac.uk/ 12036/1/110714highordermathsen.pdf

[28] 李瓊，倪玉菁．從學生數學學習的追蹤研究看新課程改革的實施效果[J]．教育研究，2012，（5）：107-113．

[29] 張曉斌．論數學教學中思維層次的結構[J]．數學教育學報，2005，14（1）：20-22．

[30] ?Yeung S Y. Conception of Teaching Higher Order Thinking: Perspectives of Chinese Teachers in Hong Kong [J]., 2015, 26(4): 553-578.

[31] ?Pogrow S. Challenging At-Risk Students: Findings from the HOTS Program [J]., 1990, 71(5): 389-397.

[32] ?Weiss R E. Designing Problems to Promote Higher-Order Thinking [J]., 2003, (95): 25-31.

[33] ?Caine RN, Caine G, McClintic C, et al.[M]. Corwin Press, 2015.

[34] ?Stein M K, Smith M S. Mathematical Tasks as a Framework for Reflection: From Research To Practice [J]., 1998, 3(4): 268-275.

[35] ?Budsankom P, Sawangboon T, Damrongpanit S, et al. Factors Affecting Higher Order Thinking Skills of Students: A Meta-Analytic Structural Equation Modeling Study [J]., 2015, 10(19): 39-52.

[36] 季素月．創新意識的培養與數學學習環境的重建[J]．數學教育學報，2001，10（4）：21-24．

[37] ?Polya G.[M]. Princeton University Press, 2014.

[38] 袁志玲，陸書環．高認知水平數學教學任務的特征分析[J]．數學教育學報，2006，15（4）：24-28．

[39] 袁志玲，陸書環．高認知水平數學教學任務的教學意義及啟示[J]．數學教育學報，2008，17（6）：37-40．

[40] 戴再平．開放題：數學教學的新模式[M]．上海：上海教育出版社，2002．

[41] 寧連華．數學探究教學設計研究[J]．數學教育學報，2006，15（4）：39-51．

[42] ?Raiyn J, Tilchin O. Higher-Order Thinking Development through Adaptive Problem-Based Learning [J]., 2015, 3(4): 93-100.

[43] ?Irvine J, Telford W, Anusic V, et al. A Straightforward Model Eliciting Activity and the Power of “What If?” in Supporting Students’ Higher-Order Thinking [J]., 2016, (3):7-22.

[44] ?Abbas S, Al-Sayed R. A Program Based on Developmental Mathematics Approach to Develop Higher Order Mathematical Thinking Levels and Mathematics Appreciation for Primary Stage Students [J]., 2016, 136(3): 378-390.

[45] ?Staples M E, Truxaw M P. An Initial Framework for the Language of Higher-Order Thinking Mathematics Practices [J]., 2012, 24(3): 257-281.

[46] 潘巧明，張維忠．計算機技術與數學創造性思維培養[J]．數學教育學報，2002，11（4）：59-62．

[47] ?Susanti E, Kusumah YS, Sabandar J, et al. Computer-Assisted Realistic Mathematics Education for Enhancing Students’ Higher-Order Thinking Skills [J]., 2014, 5(18): 51-58.

[48] ?Collins G W, Knoetze J G. Information Communication Technology in the Form of an Expert System Shell as a Cognitive Tool to Facilitate Higher-Order Thinking [J]., 2014, 30(4): 455-471.

[49] ?Wang, Xu, Miaomiao Wen, et al.[R]. The Sixth International Conference on Learning Analytics & Knowledge, New York, The USA, 2016.

[50] 程華．初中數學合作學習的調查與思考[J]．數學教育學報，2010，19（2）：62-65．

[51] 韓琴，胡衛平，賈小娟．同伴互動小組結構對小學生創造性問題提出的影響[J]．心理科學，2013，（2）：417-423．

[52] ?Brookhart S M.[M]. Alexandria, The USA: Association for Supervision & Curriculum Development (ASCD), 2010.

[53] ?Newmann F M, King M B, Carmichael D L. Authentic Instruction and Assessment [EB/OL]. http://teacherlink.ed. usu.edu/nmsmithpages/IREX2012/Readings/Spencer/Authentic-Instruction-Assessment-BlueBook.pdf

[54] ?Kulm G.[M]. Washington DC: American Association for the Advancement of Science, 1990.

[55] 鮑建生，周超．數學學習的心理基礎與過程[M]．上海：上海教育出版社，2009．

[56] 范良火．高層次數學能力和課堂書面筆試的實施——從新加坡課堂實踐和研究得到的認識[J]．數學教育學報，2006，15（4）：47-51．

[57] 王帥．教師課堂評價偏見：形成、效應及矯正[J]．課程·教材·教法，2014，（2）：32-38．

[58] 黃毅英．傳統數學評價之“缺憾”——以一個租船問題為例[J]．數學教育學報，2006，15（3）：8-15．

[59] ?Thompson T. An Analysis of Higher-Order Thinking on Algebra I End-of-Course Tests [EB/OL]. http://www.cimt. plymouth.ac.uk/journal/thompson.pdf

[60] ?Haladyna T M.[M]. Allyn & Bacon, 1997.

[61] ?Collins. Skills for the 21st Century: Teaching Higher-Order Thinking [J]., 2014, 12(14): 24-29.

[62] ?Wang J. TIMSS Primary and Middle School Data: Some Technical Concerns [J]., 2001, 30(6): 17-21.

[63] 鮑建生．追求卓越——從TIMSS看影響學生數學成就的因素[M]．上海：上海教育出版社，2003．

[64] ?Fan L, Zhu Y.[M]. How Chinese Learn Mathematics: Perspectives from Insiders. World Scientific, 2004.

[65] ?Bakry B, Bakar MN. The Process of Thinking among Junior High School Student in Solving HOTS Question [J]., 2015, 4(3): 138-145.

[66] ?AgusBudiman. Developing an Assessment Instrument of Higher Order Thinking Skill (HOTs) [A]. In:[C]. International Conference On Research, Implementation and Education of Mathematics and Sciences, Yogyakarta, The USA, 2015.

[責任編校：周學智]

Review of Domestic and Foreign Research on Higher Order (Mathematical) Thinking

CHANG Lei

(The Department of Mathematics, East China Normal University, Shanghai 200241, China)

Higher order thinking (HOT) has been one of the hot issues of education research in recent years. HOT research mainly focused on definition, learning and instruction, assessment and so on. There are several kinds of definition of HOT, and they are significantly different; learning and instruction research for HOT involves many aspects, and trends to combine with new technology; the assessment research for HOT is in developing and improving. These studies may give implications for promoting the theoretical and empirical researches on higher order mathematical thinking in China, which include: strengthen the definition study of higher order mathematical thinking; improve the empirical research on higher order mathematical thinking; establishing the evaluation system for higher order mathematical thinking.

higher order (mathematical) thinking skills; definition; learning and instruction; assessment

G40-03

A

1004–9894（2016）05–0009–07

2016–04–13

2014年國家建設高水平大學公派研究生項目——國家留學基金委資助華東師范大學數學系與澳大利亞墨爾本大學墨爾本教育研究學院聯合培養博士生（留金發[2014]3026號）；2015年度上海市教育科學研究重大項目——中小學數學教材的有效設計，子課題1——中小學數學課程內容發展主線的頂層設計（D1508）

常磊（1986—），男，河南安陽人，博士生，主要從事高層次數學思維能力和數學教學情境研究．